基于ERA5的南大西洋风速和有效波高时空变化特征分析
夏武松,魏永亮,陆恒星,周 楠
(1.上海海洋大学 海洋科学学院,上海 201306;2.中国气象局上海台风研究所,上海 200030;3.上海能源科技发展有限公司,上海 200233;4.上海河口海洋测绘工程技术研究中心,上海 201306;5.上海海洋大学 国际海洋研究中心,上海 201306)
引 言
在全球气候变暖背景下,大气与海洋的研究显得尤为重要,而海表风速和包括有效波高在内的各种海浪要素又在大气和海洋研究中扮演重要角色。风速的变化以及由海表风速引起的海面波动,是海-气相互作用过程的重要因素。南大西洋洋面广阔,其海表风速和有效波高的变化受天气系统影响,因此,开展南大西洋风速和有效波高的时空特征研究有助于更科学地认识气候变化及海-气相互作用机理。
精确的海洋数据对海洋研究具有重要意义,南大西洋风场和海浪场的研究起初主要依赖于船舶气象资料。南大西洋平均浪高、涌高及大浪大涌频率的分布形式都是高纬大于低纬,东部大于西部[1]。全年风场比较相似,风向基本以30°S,15°W为中心逆时针方向旋转[2]。随着卫星高度计的发展以及数值模式的建立,越来越多的海洋资料得以发现,前人对风速和有效波高的研究也拓展到其它海域。太平洋波高分布具有明显的季节变化规律,且与太平洋的风速分布特征具有良好的对应关系[3]。南海-北印度洋的海表风速和有效波高之间存在5.2 a左右的共同周期[4]。海浪在印度洋、大西洋的低纬度区域及太平洋东岸的低纬度区域有弱的增加趋势;在30°S~45°S的南太平洋区域增加趋势较强[5]。海浪过程是风输入能量向次表层海洋传播的一个重要途径,但是二者间互相影响的内在机制还需要进一步深入研究[6]。北太平洋海域中低纬波高逐年线性递增,波高和风速都有明显的季节变化特征[7]。热带北大西洋和北太平洋高纬度海区风速呈增大趋势[8]。1962—1986年期间东北大西洋有效波高呈线性增加[9]。前人对全球海域风速和波高值也做过相关研究,Young等[10]利用卫星同化资料研究发现风速在全球大部分海域呈年际递增趋势,而波高的增加程度较小,但极端波高值在中高纬度呈递增趋势。Zheng等[11]利用CCMP(Cross-Calibrated Multi-Platform)风场资料研究发现1988—2011年期间,全球海表风速以3.35 cm/(s·a)增速上升。风速线性递增趋势主要集中在南半球西风带、北太平洋高纬度、印度洋30°S以北、大西洋低纬度海域[12]。前人对南大西洋风速和有效波高在气候变化背景下的时空变化特征及成因研究较少,对此开展研究可以补充对南大西洋海域风场和浪场的科学认识,能深入了解全球气候变暖背景下,南大西洋海浪及海表风速所受的影响,也能为南大西洋与其它大洋对全球气候变暖的响应对比提供科学依据。
本文利用1979—2019年欧洲中期天气预报中心(ECMWF)ERA5再分析资料中的风速、有效波高逐月数据,分析其多年平均和季节分布特征,并利用一元线性回归统计模型、Pearson显著性检验法及Mann-Kendall检验法分析其年际变化特征。最后利用EOF经验正交函数分解法深入研究风速、有效波高的分布特征。
1 数据与方法
1.1 数据来源
此次研究的数据来源于欧洲中期天气预报中心(ECMWF)的ERA5再分析资料,其基于ECMWF综合预报系统(IFS version Cycle41r2)模拟得到[12],ERA5再分析资料在其前身ERA-interim基础上有明显改进,首先是时空分辨率得到大幅提升,从地面到0.01 hpa高空(约79 km)分为137个垂向σ层,水平分辨率为31 km(约0.25°),时间分辨率从6 h提升到1 h。此外,大量历史观测数据,尤其是卫星观测数据利用先进的四维变量资料同化系统(4D-Var)同化到ERA5数据集中。ERA5提供240个变量,其中包括耦合波模型提供的波高和波向。
基于ERA5数据集,用户能够更加准确地分析过去的大气与海洋状态。许多专家学者利用此数据研究大气和海洋,如Patra等[13]利用ERA5再分析数据和卫星高度计数据,研究了1992—2016年主要气候变化模式对全球极高波高度的影响。Aboobacker等[14]利用ERA5再分析资料中共40年的风速和波高数据,分析了阿拉伯海、红海和波斯湾海域极大北风和有效波高。本文选择的研究区域为0°S~70°S,70°W~30°E,针对此研究区域,提取1979—2019年ERA5月平均10 m风场数据,空间分辨率为0.25°×0.25°,有效波高空间分辨率为0.5°×0.5°。
1.2 研究方法
1.2.1 M-K(Mann-Kendall)突变检验
Mann-Kendall检验法是一种非参数统计检验方法,即假定了随机变量的分布,该方法被广泛应用于气候资料分析,能够检验序列的变化趋势,最初由H. B. Mann和M. G. Kendall提出该原理并发展了这一方法,故称为Mann-Kendall法[15-16]。本文利用M-K检验法对风速和有效波高的变化趋势及突变点进行研究。具体方法如下,对于具有n个样本量的时间序列x,构造一秩序列:
(1)
(2)
式中,k为时间序列;i值范围为1~k;xi为1979—2019年风速或有效波高值;ri表示第i个样本xi大于xj(1≤j≤i)的累计数。
秩序列Sk是第i时刻数值大于j时刻数值个数的累计数,在时间序列随机独立的假定下, 定义统计量UFk:
(3)
式中,UF1=0;var(Sk)是累计数Sk的均值和方差。
在x1,x2,…,xn相互独立且具有相同连续分布时,它们可由式(4)、式(5)算出:
(4)
(5)
1.2.2 EOF分析
EOF经验正交函数分析方法,是一种分析矩阵数据中的结构特征,提取主要数据特征量的方法,最早是由Pearson提出来的[17],如今在海洋科学及其他学科中得到了非常广泛的应用。海洋科学数据分析中通常将特征向量对应的空间样本称为空间模态,将对应时间变化的主成分称为时间系数,所以海洋科学中也将EOF分析称为时空分解,其基本思想是将变量场观测资料的矩阵形式分解为空间函数和时间函数两部分的乘积之和。本文采用EOF分解对南大西洋1979—2019年间的风速、有效波高进行展开,过滤掉随机干扰,只保留统计上最显著的两个典型模态,研究风速、有效波高的空间分布特征和变化趋势。
EOF展开:
(6)
写为矩阵形式:
X=VT
(7)
式中,m是空间点,本文研究中将其视为网格点;n是时间点,即观测次数;xij表示在第i个网格点上的第j次观测值。先求出XTX的特征值和特征向量,借此求出XXT阵的特征向量。
2 风速和有效波高的年平均和季节分布特征
2.1 风速年平均分布特征
为分析风速1979—2019年平均分布特征,将初始风速数据进行多年平均。
图1是1979—2019年风速多年平均分布图,以便分析风速分布的区域差异。风速主要受信风、副高、盛行西风、南极低压等天气系统的影响。低纬度0°S~15°S海域,主要受信风控制,平均风速在6 m/s以上,西部海域风速高于东部,这是由于信风在传播过程中受到非洲大陆的摩擦作用。信风在西部海域传播,无陆地摩擦便形成风速大值区(方框),平均风速在7 m/s以上。15°S~40°S海域风速主要受副高控制,副高区以垂向风为主,所以水平风速较低,风向以低值区(30°S,10°W附近)为中心逆向旋转。副高边缘风速等值线较为密集,说明此区域风速梯度大。40°S~60°S区域,风速主要受盛行西风控制,风速基本在5 m/s以上,最大可达8.5 m/s,且东部海域风速大于西部,这是由于阿根廷以东洋面,无大陆阻隔,使得西风带风速可继续向东发展。在60°S~70°S区域,风速主要受低压影响,平均风速在3 m/s左右,风向以西风和西南风为主。

图1 1979—2019年平均风速分布
2.2 风速季节分布特征
为分析风速季节分布特征,将各季节代表月的风速进行多年平均。
图2是风速的季节分布图,信风区(0°S~30°S),风向以SE为主,春季(图2a)有两个大值中心,风速在7.5 m/s以上,夏季(图2b)和秋季(图2c)有所减小,冬季(图2d)大值中心变为一个,风速在8 m/s以上。副高区(30°S附近),风向变化较大,大致以特里斯坦-达库尼亚群岛(35°S,15°W)为中心逆时针方向旋转。全年风速在2.5 m/s左右,季节变化不明显,但副高纬度范围有所变化,冬季相比其它季节明显缩小。西风带(40°S~60°S),风向以W为主,从等值线的南北跨度可以看出,冬季西风带控制范围较其他季节更广,风速大值区也有所扩大,风速最大可达8.5 m/s。低压区,风向以SW为主,全年风速在2.5 m/s左右,季节变化不明显。
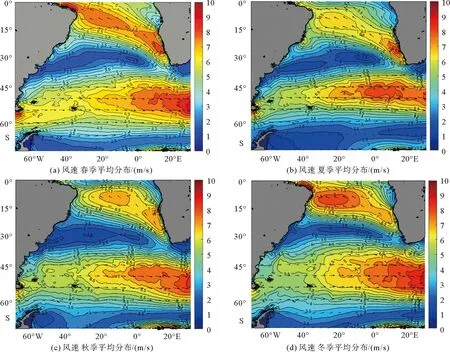
图2 风速季节分布
为分析季节间风速分布差异,对风速求差值。图3为各季节间差值分布,图3(a)是夏季-春季差值分布,正差值主要分布于15°S~50°S海域,三个正差值中心值在1 m/s左右,其它大部分海域风速差值均为负,最大负差值为-3 m/s。图3(b)正差值主要分布于信风带和西风带,且在30°S~50°S之间有一舌状分布的正差值区,其它海域风速差值基本为负。图3(c)30°S~45°S之间有一较明显的舌状正差值区,最大正差值为2.75 m/s。说明此区域季节差异较为明显。图3(d)负差值主要分布于30°S~45°S范围海域,正差值主要分布在60°S附近。图3(e)正差值区分布于绝大部分海域,且正差值最大可达2.75 m/s,而负差值分布区较小,说明冬季风速整体高于夏季。图3(f)正差值区分布于大部分海域,说明春季风速整体强于秋季。整体来看,冬季风速明显高于其他季节。与闫明等[2]得到的南大西洋平均风速的最强季节是冬季的研究结果基本一致。
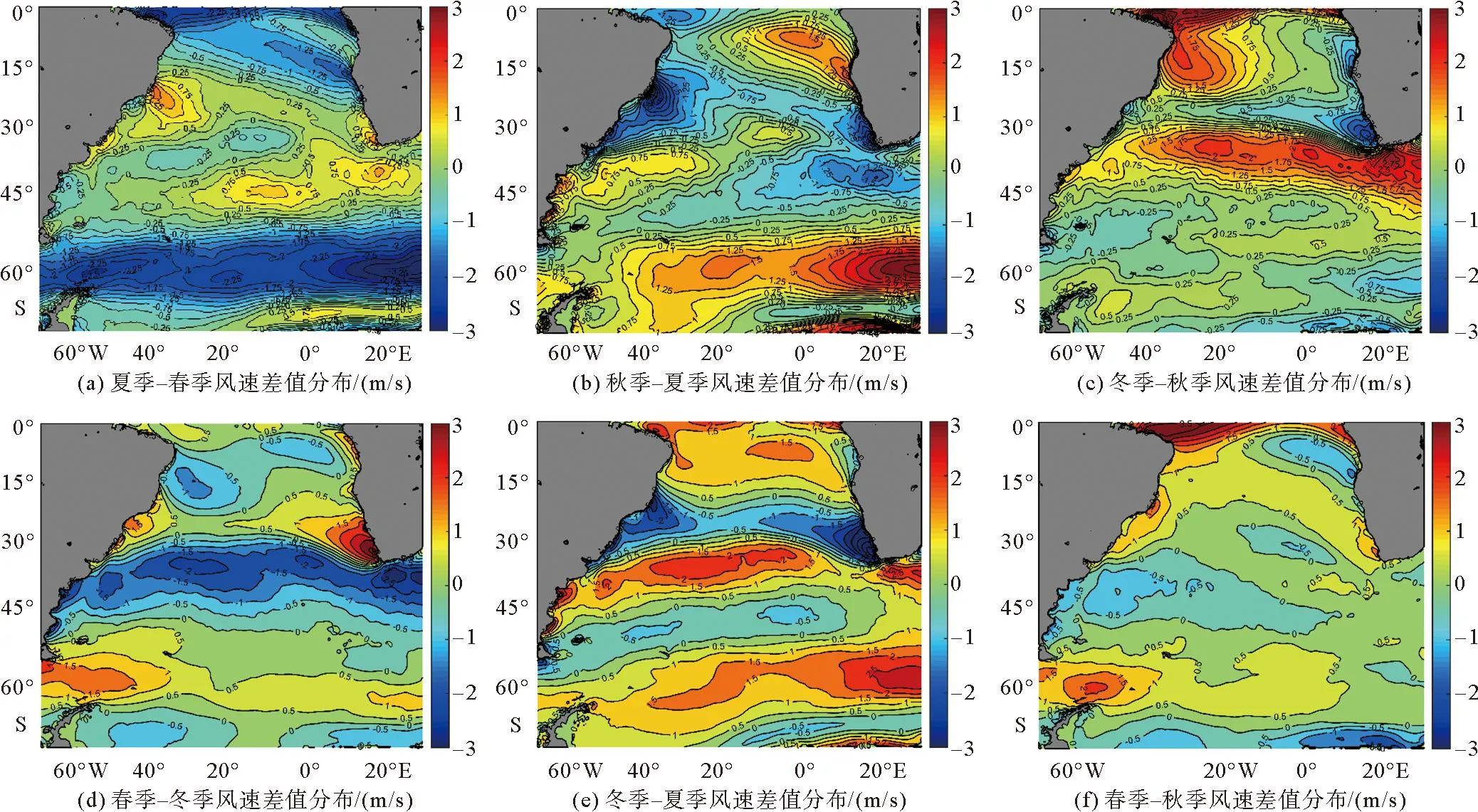
图3 风速差值分布
2.3 有效波高年平均分布特征
为分析有效波高年平均分布特征,对数据进行多年平均。
图4是有效波高年平均分布图,0°S~30°S海域平均有效波高在2.25 m以下,且近岸海域低于外海。其中0°S~15°S区域中2 m等值线和15°S~30°S区域中2.25 m等值线突出部分,与前文分析中对应海域的风速大值区等值线基本一致。30°S~40°S范围海域较低纬度海域有所增加,平均有效波高在2.25~3.25 m。此区域等值线分布均匀,由低纬到高纬均匀增加0.25 m。40°S~60°S范围海域平均高度在3.25 m以上,且东部海域高于西部海域,与前文风速分布一致。60°S~70°S范围均在2 m以下,对应区域风速也较小,波高较小与海冰分布有关。整体来看,有效波高分布特征与风速基本一致,即风速较大的海域对应较高的有效波高,且二者都呈纬向环状型空间分布特征。
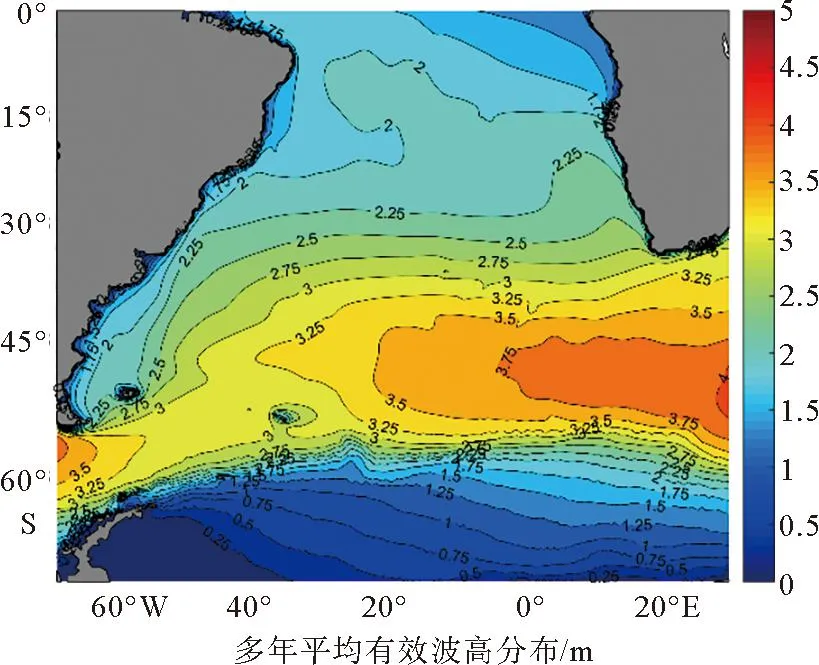
图4 1979—2019年平均有效波高分布
2.4 有效波高季节分布特征
为分析有效波高季节分布特征,将各季节代表月的有效波高数据进行多年平均。
图5为有效波高季节分布,0°S~30°S海域季节变化较小,全年均在2 m左右,冬季阿森松岛以南大部分海域2.25 m以上。30°S~60°S海域季节分布差异明显,冬季(图5d)大值区明显高于其它季节,最大波高可达4.5 m,秋季(图5c)次之,最大可达4 m,春季(图5a)和夏季(图5b)分别可达3.75 m和3.25 m。此区域有效波高分布和风速一致,即风速大值区对应波高大值区,东部海域有效波高大于西部。60°S~70°S海域由于海冰的存在,使得春季和冬季无波高,夏季均在2.5 m以下,而秋季在3.25 m以下,且都随纬度增加而减小,这是由于越靠近南极地区,海冰覆盖范围越大。
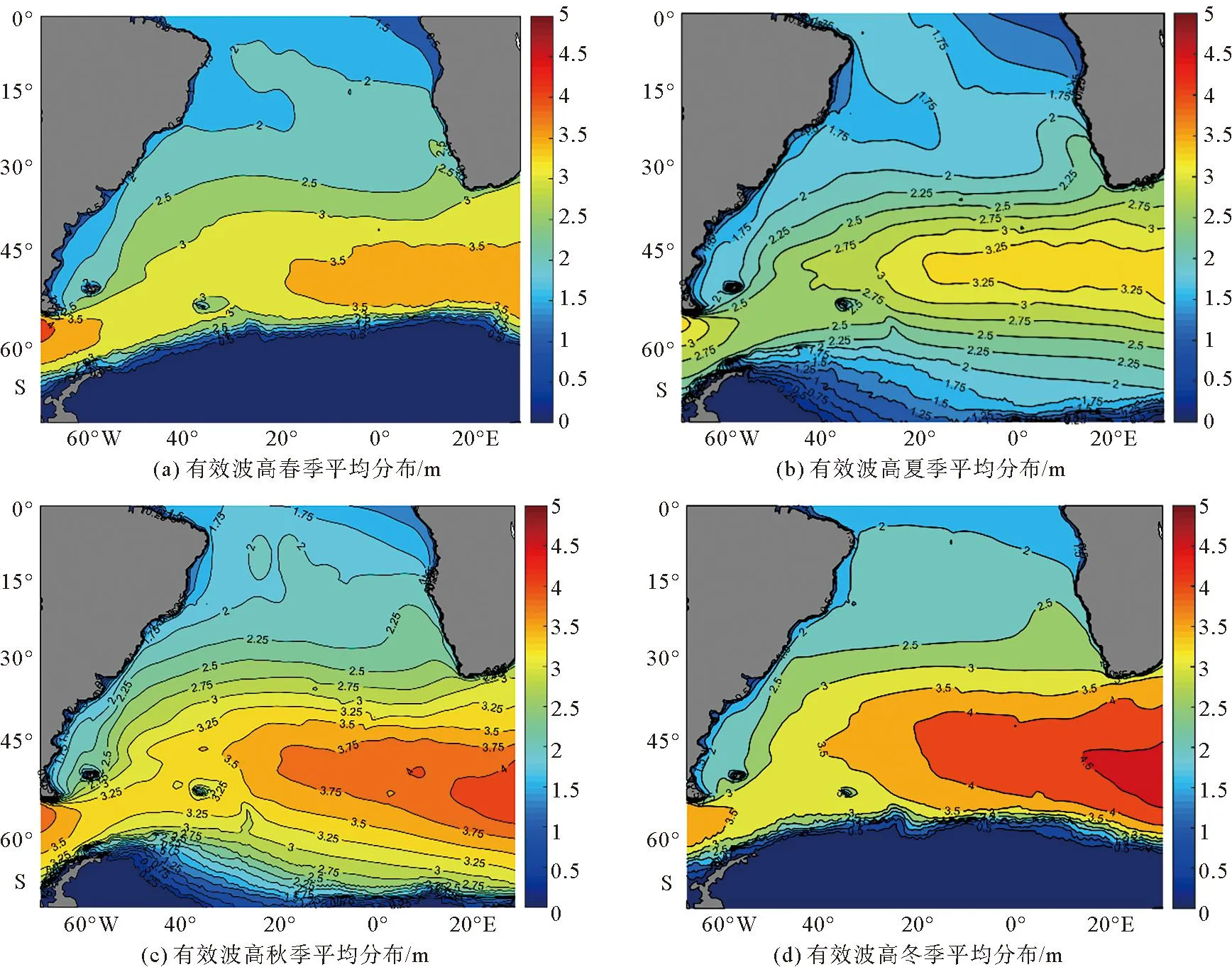
图5 有效波高季节分布
为分析季节间有效波高分布差异,对有效波高求差值。图6(a)是冬季-夏季有效波高的差值分布,正差值几乎分布于60°S以北所有海域,中心分别位于30°S~40°S之间的中部海域以及45°S~60°S之间的最东部海域,最大均超过1 m。图6(b)是秋季-春季的差值分布,正差值几乎覆盖15°S以南所有海域,15°S~60°S海域均在1 m以下,而60°S-70°S范围最大可达3.75 m,这是由于春季海冰的存在。

图6 有效波高差值分布
3 风速与有效波高相关性分析
前文提到风速高的海域,有效波高也相对较大,为验证这一结论,对多年风速与有效波高进行相关性分析,从图7可以看出,信风和西风带控制区大部分海域风速和有效波高的相关系数通过了95%的显著性检验,表明风速和有效波高有很强的相关性,从而验证了前文结论。

图7 风速与有效波高相关系数分布(打点表示通过95%的显著性检验)
4 风速与有效波高的变化趋势
将风速和有效波高数据进行区域平均,得到区域年平均值。图8(a)和(b)分析了41年风速和有效波高的线性变化趋势,图8(c)和(d)分析了风速和有效波高变化的Mann-Kendall检验的UF和UB统计量。
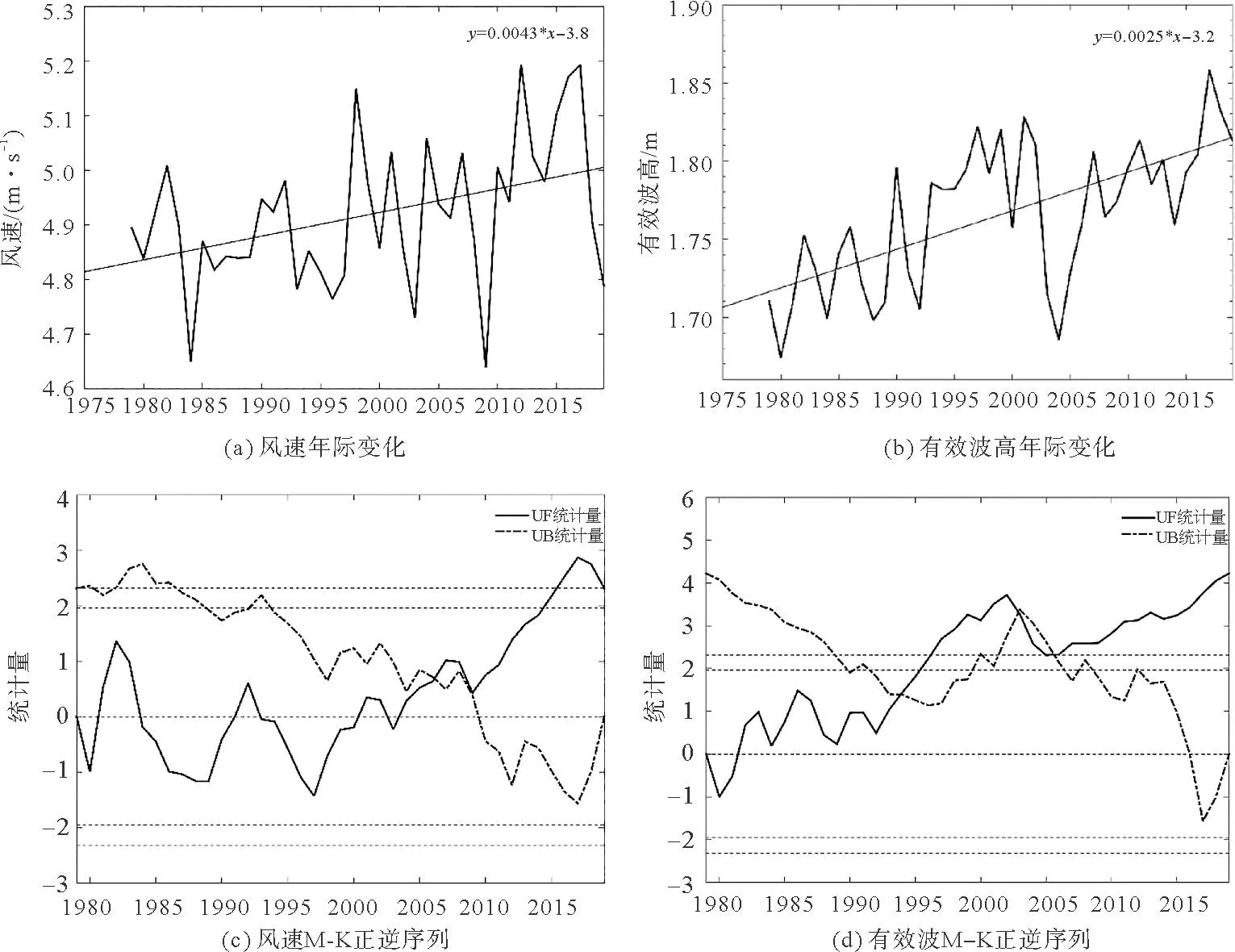
图8 1979—2019年风速与有效波高年际变化和M-K检验(实线为UF,虚线为UB,水平线分别为0值线、0.05和0.01信度检验临界值)
从图8(a)可以看出,风速呈线性递增趋势,通过了0.05的显著性检验。三段式变化特征: 1997年以前围绕4.86 m/s上下波动。1998—2008年期间,在4.95 m/s左右波动。2009—2019年期间,在5 m/s左右波动。整体来看,风速分别在2009年降至最小值4.638 m/s,2012年达到最大值5.194 m/s,总体呈波动式上升趋势,只有个别年份存在“陡降”或“陡升”现象。风速的递增趋势现象与前人的相关研究结果基本一致(Zheng等[11])。图8(c)是风速变化的Mann-Kendall检验,2009年之前UB曲线大于0,表明在此期间风速处于增加趋势,而2004—2019年UF值大于0,说明风速整体是上升趋势。UF和UB曲线在2006和2009年存在明显交点,且交点都位于临界线之间,结合距平值及变化曲线(a),可确定2006和2009年附近出现突变。风速突变原因与西风带、信风的加强或减弱相关,因为副高区主要为下沉气流,所以水平风速的突变可从西风和信风加强或减弱来解释,进一步研究可通过对西风和信风区风速求区域平均来验证。
从图8(b)可以看出,有效波高也呈线性递增趋势,通过了0.01的显著性检验。三段式变化特征:1979—1993年期间,呈明显的波动式上升趋势,此期间均值为1.73 m。1994—2004年期间,在1.78 m左右波动。2005—2019年也呈波动式上升趋势,此期间均值为1.8 m。这种上升趋势与Young等[10]的研究结果一致, IPCC第五次科学评估报告也指出全球海平面有上升趋势,所以在全球气候变暖背景下,有效波高很可能会随海平面上升而继续增大[18]。图8(d)为有效波高变化的Mann-Kendall检验,1979—2019年UF和UB曲线整体上均大于0,说明在此期间处于增大趋势,UF和UB曲线在1994、2003、2006年存在交点,但只有1994年的交点位于临界线之间,结合距平值和有效波高变化曲线(b),可确定1994年附近出现突变。因为全球海洋的背景场主要由涌浪主导[19],且涌浪传播速度较快,常先于天气系统抵达[20],所以有效波高的突变会先于风速。
5 风速和有效波高空间分布EOF分析
5.1 风速空间分布EOF分析
为了验证风速年际变化特征是否具有一致性,使用EOF经验正交函数分析法对1979—2019风速提取典型模态场。表1为前两个模态的方差贡献率,分别为81.30%和5.56%,累积方差贡献率达到86.86%。故前两个模态能反映主要空间分布特征,且第一模态是风速空间分布变化的主要形式,因此仅分析第一模态的特征。
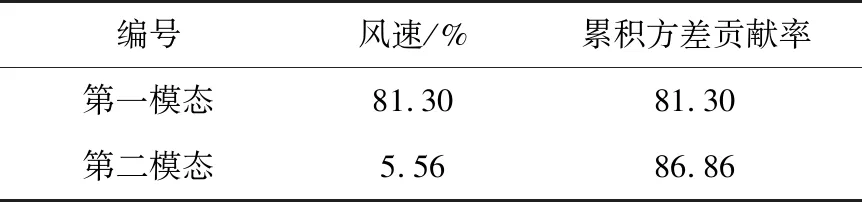
表1 风速前两个主要模态的方差贡献率
图9(a)为风速空间分布第一模态,图9(b)为对应的时间系数序列。从图9(a)来看,风速变率正值区主要位于信风带和西风带控制区,正值中心位于25°W,12°S、8°E,22°S、30°E,50°S附近。负值区主要位于副高和低压控制区,且副高控制区有一低值中心位于10°W,30°S附近。而零线走向沿着副高控制区边缘,说明风速的空间分布主要呈信风带-西风带和副高-低压带反向型,即信风区和西风带控制区为“+”,副高和低压带控制区为“—”。结合时间序列(图9b)可知,时间系数均为正值,且整体上有缓慢递增趋势(通过了0.05显著性检验),表明信风区和西风带控制区风速呈一致变化型,是正位相,即均为显著上升趋势,而副高和低压带控制区风速呈一致变化型,是负位相,即均为显著下降趋势。所以不同控制区风速的年际变化趋势不同,但前文分析结果以及前人相关研究成果都表明风速具有年际递增趋势,说明信风区和西风带控制区风速的递增趋势比副高和低压带控制区风速的下降趋势更为明显。
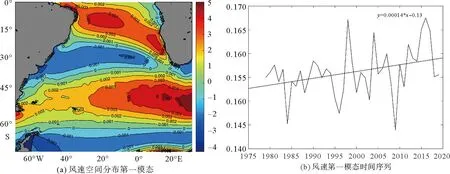
图9 风速分布第一模态(a)及对应的时间序列(b)
5.2 有效波高空间分布EOF分析
表2为有效波高前两个主要模态的方差贡献率,分别为85.69%和4.09%,累积方差贡献率达到89.78%。故取前两个模态分析能充分反映有效波高变化的空间分布特征,且第一模态是空间分布变化的主要形式,因此仅分析第一模态。
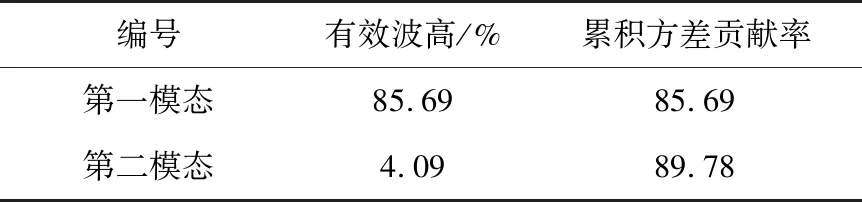
表2 有效波高前两个主要模态的方差贡献率
图10(a)是空间分布第一模态,图10(b)为对应的时间系数序列。从图10(a)来看,变率正负值区主要以60°S为界,主要呈北“+”南“-”的分布特征。零线走向在中高纬与60°S纬线基本平行,负值中心位于50°S,20°E附近,正值中心位于67°S,60°W附近。结合图(b)时间系数序列来看,由于时间系数均为负值,且有递减趋势(通过了0.01显著性检验),表明60°S以北为正位相,以南为负位相,即正位相区域增大趋势显著,负位相区域减小趋势显著。结合风速分布EOF分析可知,副高控制区风速有减小趋势,但有效波高却有增大趋势,且南美洲大陆近岸海域有效波高呈减小趋势,有效波高的这种变化趋势和风速之间未能形成良好的对应关系,说明风速只是影响有效波高的因素之一,近岸地形的摩擦效应导致浪在传播过程中能量耗散也是可能因素。
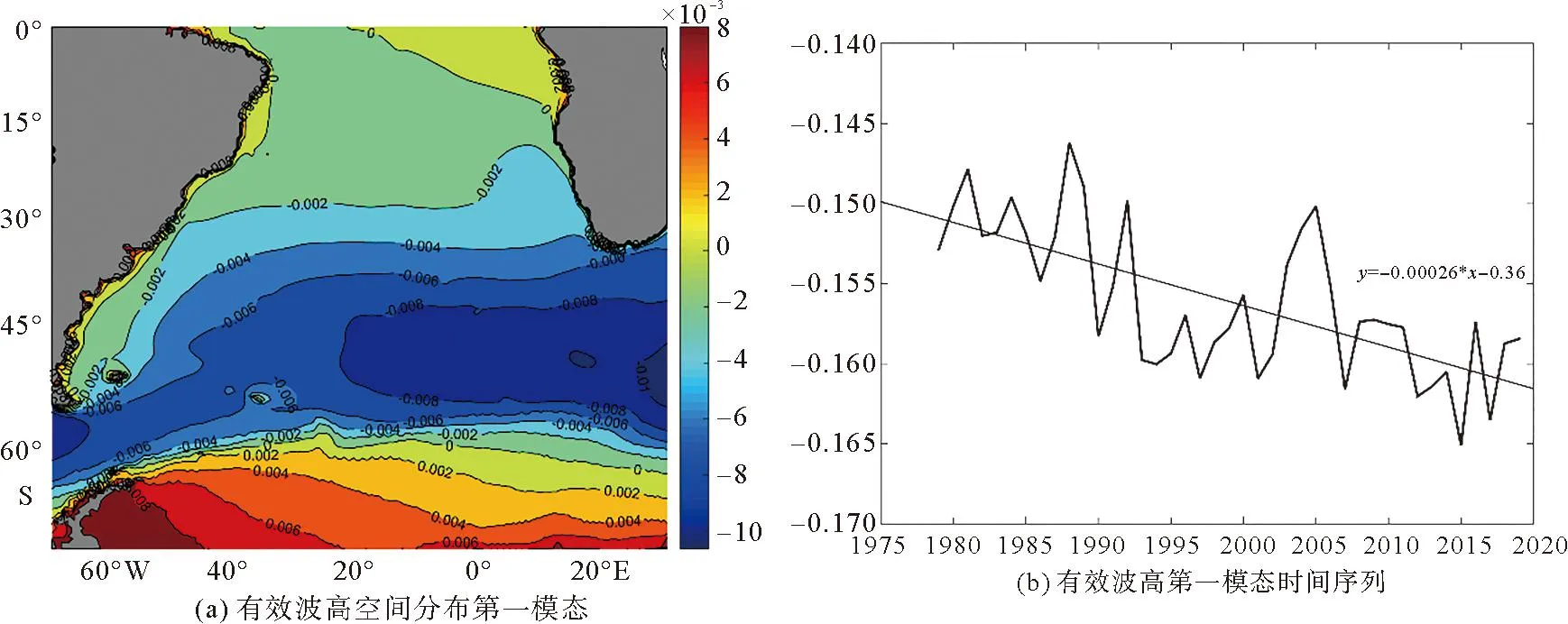
图10 有效波高分布第一模态(a)及对应的时间序列(b)
6 结论
本文分析了南大西洋风速和有效波高的年平均和季节分布特征,利用Mann-Kendall检验对1979—2019年风速和有效波高的变化趋势进行探讨,以及用EOF经验正交函数法分析风速和有效波高的空间分布特征,主要结论如下:
(1)风速的年平均分布特征明显,大值区主要分布在信风和西风带控制区,低值区主要分布在副高和低压带控制区。风速的季节分布差异明显,冬季风速明显高于其他季节,不同纬度风速分布有明显的季节特征,全年风速、风向分布和天气系统特征有关。
(2)有效波高分布和风速类似,风速大值区对应波高大值区。有效波高的分布在不同纬度也有明显的季节特征,春季和冬季高纬度海域波高为0,中高纬度冬季有效波高全年最大。
(3)风速年际变化呈波动式上升趋势,且个别年份存在陡升或陡降现象。M-K检验结果也表明风速的年际变化整体呈上升趋势,且在2006和2009年附近出现突变。有效波高年际变化与风速类似,但突变点较风速提前,出现在1994年前后。
(4)风速EOF第一模态信风带-西风带和副高-低压带控制区风速呈反向型分布,前两者控制区风速呈上升趋势,后两者控制区风速呈下降趋势。有效波高EOF第一模态显示60°S以北海域有效波高增大趋势显著,以南则相反,副高控制区以及南美大陆近岸海域风速与有效波高分布未能形成对应关系。影响有效波高变化的因素较为复杂,深入研究地形的摩擦效应、海温以及天气系统的变化是解释有效波高变化的可行方案。

