非常规油气井用套管抗挤毁性能有限元分析*

汪 强，晁利宁，白天娇，焦 炜，苑清英，杨晓龙，郭 鹏

（1.中油国家石油天然气管材工程技术研究中心有限公司，西安 710018；2.中国石油宝鸡石油钢管有限责任公司，陕西 宝鸡 721008；3.中石油煤层气有限责任公司 北京物资分公司，北京 102206）

0 前 言

随着我国石油勘探水平的不断提高，深井、超深井、热采井以及高温高压气井的数量逐年增加，地层环境愈来愈复杂，对套管的性能提出了更高的要求。在页岩气、致密气等非常规油气井开采中，套管的抗外挤性能已成为管柱设计最重要的依据[1-3]。引起套管挤扁、缩径、错段、损坏的原因是复杂的，但根本原因是在地层应力作用下套管所受外部载荷超过了套管的抗外压载荷强度[4]。

通常影响套管抗挤性能的因素主要包括几何精度、屈服强度、狗腿度等。国内外针对套管抗挤毁强度问题开展了大量的有限元分析[5-8]，但在分析过程中，通常假定钢级一定且屈服强度均一[9]，未充分考虑屈服强度在管体周向的不均匀对套管抗挤毁强度的影响，且在众多变化因素中未得出影响抗挤毁强度的主要因素及次要因素。

本研究在国内外有限元分析研究的基础上，在规格和钢级确定的条件下，充分考虑套管本体和井下受力情况，针对几何尺寸缺欠、屈服强度变化等因素，建立有限元模型，并基于弧长法进行套管抗挤毁性能分析，研究均匀外压作用下，外径椭圆度、壁厚不均度、屈服强度不均匀分布等因素对套管抗挤毁性能的影响规律。

1 分析方法及模型建立

1.1 数值分析计算

API SPEC 5C3 标准[10]规定，无轴向载荷和内压作用下，管体最小抗挤毁强度由材料最小屈服应力fymn和管体横截面几何尺寸确定。可分为屈服强度挤毁压力PYp、塑性挤毁压力Pp、过渡挤毁压力PT和塑弹性挤毁压力PE。

式中：Ac、Bc、Cc、Fc、Gc——计算管体挤毁压力的经验系数；

D——管体直径，mm；

t——管体壁厚，mm。

最小屈服强度挤毁压力公式（1）适用范围为（D/t）≤（D/t）yp，最小塑性挤毁压力公式（2）适用范围为（D/t)yp≤（D/t）≤（D/t)pt，过渡挤毁压力公式（3）适用范围为（D/t）yp≤（D/t）≤（D/t）te，弹性挤毁压力公式（4）适用范围为（D/t）te≤（D/t）。以P110 钢级Φ139.7 mm×10.54 mm 套管为例，D/t=13.25，依照API SPEC 5C3 标准相关规定，确定采用公式（2） 进行套管抗挤毁强度计算，此时Ac取值3.181，Bc取值0.081 9，Cc取值2 852。

1.2 产品条件及因素分析

针对API套管，开展套管抗挤毁性能分析。为确保套管具有优异的抗挤毁性能，通常需对套管的椭圆度、壁厚不均度进行控制。API SPEC 5CT—2018 标准规定了套管的外径、壁厚及屈服强度范围，但未对管材的椭圆度和壁厚不均度范围进行明确规定[11]。本研究在标准要求的基础上，结合P110 钢级Φ139.7 mm×10.54 mm套管实际情况，确定了几何尺寸范围和力学性能。在有限元计算过程中，屈服强度在API SPEC 5CT—2018 标准要求范围内间隔取值。几何尺寸要求见表1，力学性能参数见表2。

表1 P110钢级Φ139.7 mm×10.54 mm套管几何尺寸

表2 P110钢级材料性能参数

1.3 有限元分析方法及基本假设

针对表1和表2中的外径椭圆度、壁厚不均度和屈服强度3个变量因素，进行P110钢级套管抗挤毁非线性有限元屈曲模拟分析。通过引入弧长因子ΔL，将载荷因子λ和位移增量{ΔU}相联系，弥补了Newton-Raphson 方法极值点发散的缺点，可以精确求解屈曲载荷[12]。以此分析在API标准要求范围内，椭圆度、壁厚不均度和屈服强度不均匀分布3个因素对套管抗挤毁强度的影响情况。

1.4 建立模型

根据以上分析条件，假设套管所受外压沿周向分布均匀，不考虑套管残余应力影响。建立外径椭圆度、壁厚不均度和屈服强度变化的二维有限元分析模型。通过转换公式将试验所得工程应力-应变曲线转换为材料的真实应力-应变曲线，相邻屈服强度对应的材料参数等比例放大/缩小。采用二维平面弹塑性非线性模型进行套管抗挤毁性能分析，利用4节点单元进行网格剖分。建立的有限元几何模型及网格如图1所示，网格单元数4 400个。

根据对创业中主要困难的调查，54家样本科技型创业企业中，有75.93%的企业将融资难、融资贵列在首位，占比最高；同时有超过一半的企业认为政策支持不完善和创新创业能力不足影响企业发展。基于上述现状与问题分析，要进一步发挥众筹对科技创业的支持作用，还需强化政策支持，完善风险防控和监管措施，构建长效机制，形成协同效应，打通政策落地“最后一公里”。

图1 有限元几何模型及网格

在设定约束时，将平面沿坐标轴划分为四个象限，在每个象限边界处设置约束，确保套管不平移的前提下能够在外压作用下沿径向发生弹性及塑性变形。在管体外径上施加外压载荷，载荷线性增加，直至管体发生外压挤毁。边界条件及载荷施加情况如图2所示。

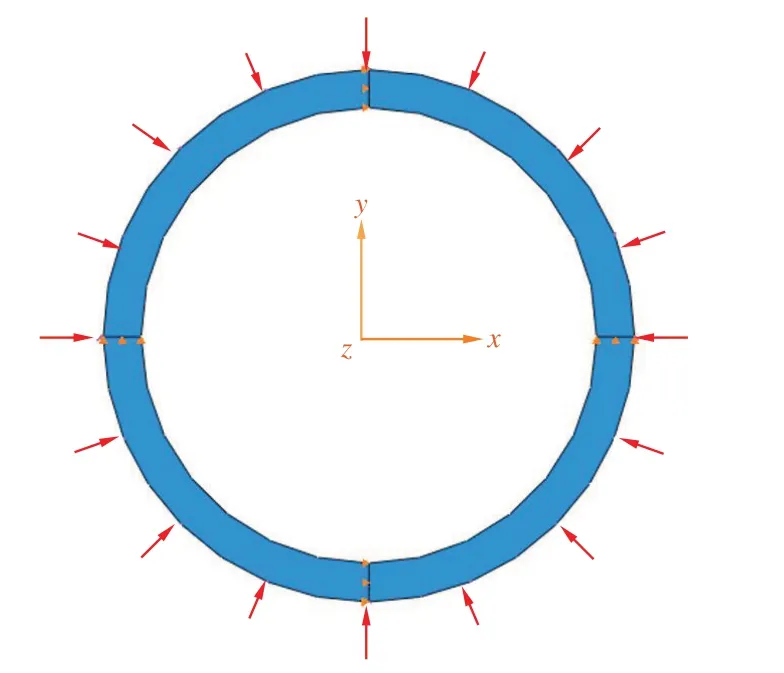
图2 边界条件及载荷施加

2 计算结果及分析

套管几何缺欠主要包括椭圆度和壁厚不均度两个方面，椭圆度及壁厚不均度又分别由最大外径、最小外径、最大壁厚、最小壁厚引起，因而其组合形式多样，考虑极限情况，通常有8种组合形式，其中壁厚偏差与椭圆外形大径方向一致时，大外径+小壁厚组合的抗外压挤毁强度相对最差，用于抗挤毁性能分析最为稳妥。故在多因素分析过程中，假设几何缺欠组合形式为壁厚偏差与椭圆外形大径方向一致，即为大外径+小壁厚组合[13]。组合形式如图3所示。

图3 壁厚偏差与椭圆外径组合示意图

2.1 几何尺寸对抗外压挤毁强度的影响分析

2.1.1 管体外径椭圆度对抗外压挤毁强度的影响

针对椭圆度变化进行套管抗外压挤毁强度有限元模拟，假设屈服强度沿周向均匀分布。椭圆度依次为0.2%、0.4%、0.6%、0.8%，壁厚不均度设定为2%。椭圆度0.4%时模拟获得的套管抗挤毁应力云图如图4所示，从图4可以看出，在外压作用初始阶段，套管应力就出现不均匀分布。套管椭圆大径方向上，套管内侧应力高于外侧；椭圆小径方向上，套管外侧应力高于内侧。外压作用至挤毁状态时，套管沿椭圆小径方向被压扁。最终，套管完全挤毁，套管内侧贴合。模拟过程中，套管承受外压初期压力逐渐升高，到达峰值后，迅速降低。三个阶段分别对应图4中的三种应力状态，峰值压力即为模拟得到的套管抗挤毁强度。

图4 壁厚不均度2%、椭圆度0.4%套管抗挤毁应力云图

模拟获得的套管抗挤毁强度与椭圆度变化关系如图5所示。从图5可以得出，随着椭圆度的增大，套管抗外压挤毁强度模拟结果逐渐降低。与理论计算结果对比发现，椭圆度较小时的模拟结果远高于理论计算结果，随着椭圆度的增大，模拟结果与理论计算结果差值逐渐减小。

图5 椭圆度变化时模拟结果与理论计算结果对比

2.1.2 管体壁厚不均度对抗外压挤毁强度的影响

在模拟分析壁厚不均度变化对套管外压挤毁强度的影响时，假设屈服强度沿周向均匀分布且套管椭圆度为0.4%。最小壁厚不变，通过最大壁厚增加调整壁厚不均度，壁厚不均度分别为2%、4%、6%、8%。模拟获得的壁厚不均度变化与套管抗挤毁强度的关系如图6所示。从图6可以得出，随着壁厚不均度的增加，套管的抗外压挤毁值模拟结果逐渐增大，且均高于理论计算结果。

图6 壁厚不均度变化时外压挤毁的模拟结果与理论计算结果对比

2.2 屈服强度变化对抗外压挤毁性能影响分析

2.2.1 屈服强度均匀整体变化

按照API SPEC 5CT 标准，当钢级一定时套管的屈服强度并不是固定值，而是在一个区间内。为此，研究分析钢级一定时，屈服强度变化对套管的外压抗挤毁性能的影响规律。屈服强度分别取800 MPa、820 MPa、840 MPa、880 MPa、920 MPa 和960 MPa，椭圆度为0.4%，壁厚不均度为2%，模拟及理论计算结果如图7 所示。从图7可以得出，随着屈服强度的升高，外压挤毁模拟结果和理论计算结果均不断升高，且模拟结果始终高于理论计算结果，但二者间的差值逐渐减小。

图7 屈服强度均匀变化时的外压挤毁模拟及理论计算结果对比

2.2.2 屈服强度分布变化

以上外压挤毁模拟分析时，均假设管体的屈服强度沿管体周向均匀分布，而实物管体的屈服强度通常沿管体周向是有差异的。为进一步分析屈服强度沿管体周向的不均匀变化对管体外压挤毁性能的影响规律，将管体沿周向划分为四个象限，每个象限分别赋予不同的屈服强度，建模时设定椭圆度0.4%、壁厚不均度2%，屈服强度分布见表3（屈服强度分布方案按均匀性优劣依次为：方案4>方案3>方案2>方案1>方案5），四个象限的平均屈服强度相同，建模象限划分如图8 所示。

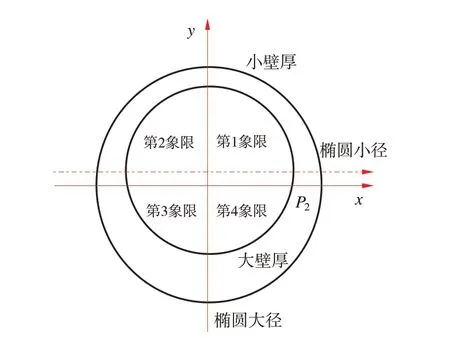
图8 沿圆周方向四个象限划分情况

表3 沿圆周方向四个象限屈服强度分布情况

模拟获得的屈服强度沿周向变化时的外压挤毁分析结果如图9 所示，结合表3 分析发现，当平均屈服强度一定时，屈服强度沿管体周向分布越均匀（方案4），套管的抗外压挤毁强度越高；屈服强度越分散（方案5），抗外压挤毁强度越低。

图9 屈服强度分布变化时的外压挤毁分析结果

3 实物外压试验与有限元分析结果对比

为了验证模拟分析得出的几何尺寸缺欠参数对套管外压挤毁结果影响规律的有效性，对P110 钢级Φ139.7 mm×10.54 mm 套管进行抗外压挤毁实物试验验证。经测量，该套管实物缺欠几何尺寸见表4。在此基础上，试验检测了套管实物的屈服强度。检测屈服强度时，将管体沿横截面化分为四个象限[14]，在每个象限内取一组拉伸试样进行试验，确定每个象限的屈服强度和抗拉强度，屈服强度检测结果见表5。取样后，剩余管样进行外压挤毁试验。外压挤毁试验方法按照SY/T 6238.1《油井管全尺寸试验方法 套管挤毁试验》执行，试样长度为3.8 m，超过8 倍的外径长度[15]，试验过程中以不超过35 MPa/min 的加压速度升压，直至套管压溃。套管实物挤毁试验曲线如图10 所示，通过实物试验得出的套管抗外压挤毁强度为116.7 MPa，外压挤毁形貌如图11所示。

图10 套管外压挤毁试验曲线

图11 套管外压挤毁后实物形貌

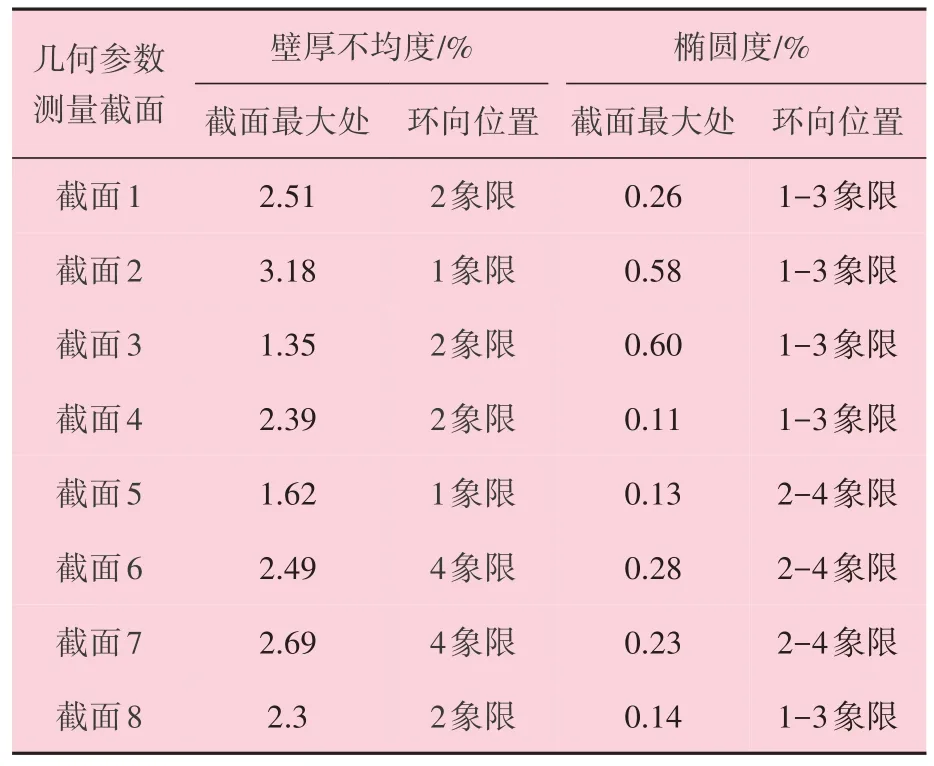
表4 套管外压挤毁实物试验缺欠几何尺寸

表5 套管实物沿圆周方向屈服强度（Rt0.6） MPa

根据模拟得到的几何尺寸缺欠影响结果可知，椭圆度比壁厚不均度对套管抗挤毁性能影响更大。截面3 位置实测壁厚不均度1.35%是样管中最小的，对应的椭圆度0.6%是样管中最大的。截面3 位置先出现变形失效，外压挤毁强度最小，是最薄弱截面。因此，根据截面3 实测的几何尺寸参数进行套管抗外压挤毁性能建模和理论计算，模拟结果得出套管实物挤毁压力为116.3 MPa，理论计算得出的实物抗外压挤毁结果为111.6 MPa。

将有限元分析得出的管体抗外压挤毁强度值与实际试验套管抗外压挤毁强度值进行对比，发现通过划分象限获取的屈服强度和实测几何尺寸建模方式模拟得出的外压挤毁结果与实物试验结果十分接近，并优于API 理论公式计算的结果，可以更加精确地预测套管实物的外压挤毁强度。

4 结 论

（1）在尺寸公差要求范围内，当套管管体几何形状存在椭圆度和壁厚不均度缺欠时，椭圆度对套管外压挤毁性能的影响大于壁厚不均度的影响。

（2）在套管椭圆度和壁厚不均度一定的情况下，随着屈服强度的均匀升高，外压挤毁模拟结果和理论计算结果均不断升高，且模拟得出的外压挤毁结果始终高于理论计算结果，但二者间的差值逐渐减小。另外，平均屈服强度一定时，管体屈服强度沿周向分布越均匀，套管的抗挤毁性能越好，但均不超过屈服强度均匀时的外压挤毁结果。

（3）根据模拟得出的几何尺寸缺欠对套管外压挤毁试验结果的影响规律，实测套管横截面的椭圆度、壁厚不均度两种几何尺寸缺欠，找出套管实物最薄弱截面。通过分象限实测屈服强度和实测几何尺寸相结合的建模方式，可以更加精确地预测套管实物的外压挤毁强度，通过开展验证试验，对比理论分析的数值模拟结果与试验测试结果，进一步验证了数值建模方法的合理性。