预制外挂墙板半刚性耗能连接节点力学性能研究*

廖 振, 梁书亭, 朱筱俊, 钱立义, 田鹏飞, 陶金鑫

(1 江苏美城建筑规划设计院有限公司南京分公司，南京 211189；2 东南大学土木工程学院，南京 211100；3 东南大学建筑设计研究院有限公司，南京 210096；4 苏州筑岳建设发展有限公司，苏州 215000)

0 引言

预制外挂墙板具有建筑立面效果好、质量可靠、绿色节能等优点,近年来逐渐得到了广泛的应用[1-2]。《预制混凝土外挂墙板应用技术标准》(JGJ/T 458—2018)[3]中将预制外挂墙板与主体结构的连接分为点线式连接与点支承式连接。点线式连接一般在墙板上部预留钢筋,墙板下部设置限位连接件,在现场与主体结构进行后浇作业,该连接方式安全可靠,但会为主体结构附加刚度。种迅等[4]开展试验研究分析了点线式支承方式对主体结构刚度与抗震性能的影响,结果表明采用点线式连接外挂墙板与主体结构会提高结构的刚度、承载力与耗能能力,随墙板与梁端叠合面脱开,墙板对主体结构刚度的影响逐渐减小。在此基础上,种迅等[5]采用金属阻尼器取代底部限位连接件,形成新型减震外挂墙板体系(EDCP),结果表明,此体系变形性能良好,在2%层间位移角加载下几乎没有损伤,底部U形金属阻尼器先于主体结构屈服,形成第一道抗震防线。Ioaanis N.等[6]采用钢筋连接外挂墙板与主体结构,试验结果表明,水平荷载下钢筋的变形较大,捏缩效应显著,外挂墙板损伤较小,但连接体系整体耗能能力较小。

点支承式连接可分为点支承平移式连接与点支承旋转式连接,分别适用于小高宽比与大高宽比的两类外挂墙板。此两类节点通过允许墙板在地震作用下发生水平滑动或摇摆旋转适应主体结构的变形,防止墙板脱落。肖明等[7]分析了点支承式连接节点的受力与变形机理,以罕遇地震不屈服的设计目标给出了地震作用动力放大系数,提出了相应的设计建议。王大伟等[8]开展振动台试验研究了外挂墙板及其连接节点的抗震性能,分析外挂墙板与主体结构间的动力响应,结果表明,设置长圆孔可实现节点的滑移,有效释放了变形,应合理设计连接螺栓的扭矩实现外挂墙板小震弹性、中震开始滑移、大震防脱落的设计目标。

此外,在欧洲针对外挂墙板开展的“Safecladding”研究计划中[9-10],相关学者还提出了多类耗能连接节点,用于外挂墙板间的连接。Liberato与Roberto等[11]提出摩擦型节点(SPAV)用于实现外挂墙板间的连接,并通过低周反复试验研究了SPAV的受力机理,以及摩擦片种类、粗糙系数、加载速率等参数的影响。Bruno等[12-14]基于摩擦机理以及金属耗能机理等,提出了螺栓摩擦节点(FBD)、W形折板节点(FPD)、菱形开缝节点(MSD)等节点,用于提高预制外挂墙板体系的抗震性能,应用上述节点的足尺结构试验结果表明,在预制墙板与主体结构间以及预制墙板间应用耗能型连接装置可以提高结构整体的耗能能力,并降低地震作用下的结构位移响应。

为提高预制外挂墙板结构的抗震性能,本文基于预制外挂墙板点支承式连接方式的变形特征,结合摩擦机理与金属弯曲机理,提出一种预制外挂墙板半刚性耗能(semi-rigid energy dissipation connection node of precast cladding panel,SEDC)节点,实现预制外挂墙板与主体结构的半刚性连接,即在风荷载与小震作用下,墙板与主体结构保持刚性连接,在大震作用下墙板可发生水平滑移适应主体结构变形,同时弯曲单元与摩擦单元共同耗能,提高主体结构的抗震性能。本文通过试验研究和数值模拟等研究方法,对SEDC受力性能进行研究,分析各设计参数的影响,为其工程应用奠定基础。

1 SEDC构造形式及受力机理分析

1.1 SEDC节点构造形式

如图1(a)所示,预制外挂墙板与主体结构采用点支承方式连接,上部两个节点为面外限位节点,下部两个节点为SEDC节点。面外限位节点的构造形式如图1(b)所示,由L形等肢角钢、螺栓、垫板以及内螺纹套筒组成,其中等肢角钢上沿水平方向开设胶囊形圆孔,内螺纹套筒分别预埋在主体结构底面以及预制外挂墙板的上部。SEDC节点的构造形式如图1(c)所示,SEDC节点由弯曲单元、摩擦单元、主体结构预埋件与墙板预埋件组成。弯曲单元由两个U形钢组成,其上下平直段上开设圆孔,以实现与主体预埋件及墙板预埋件的连接。摩擦单元由大、小摩擦板组成,小摩擦板上开设圆孔用于穿置高强螺栓,大摩擦板上开设胶囊形孔实现预制外挂墙板的滑动,大、小摩擦板上均开设有矩形槽,用于粘贴摩擦片,矩形槽的深度小于摩擦片的厚度,以使摩擦片与主体结构预埋件充分接触。大摩擦板与墙板预埋件焊接,并在两侧焊接加劲肋增大水平刚度。小摩擦板与大磨擦板间设有垫板,以实现螺栓预紧力的均匀分布。主体预埋件埋设于结构楼板顶面,其底板上焊接有内螺纹套筒以实现与U形钢连接,底板上均匀焊接锚固钢筋避免发生锚固破坏。墙板预埋件上焊接有连接钢板,连接钢板靠近焊缝处开设圆形孔便于高强螺栓穿置,其另一侧开设圆孔与U形钢连接。

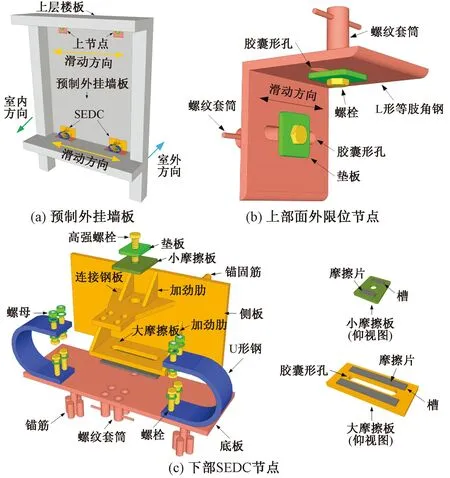
图1 预制外挂墙板及SEDC节点构造

1.2 SEDC节点受力机理

本文所提出的SEDC节点的受力性能主要可分为两个阶段,如图2所示。

图2 SEDC节点受力机理

SEDC节点的承载力P可按式(1)计算:

P=Pu+Pf=Pu+μnfPc

(1)

式中:Pu为U形钢的承载力;Pf为摩擦片的承载力;μ为摩擦系数;nf为摩擦面数量;Pc为预紧力。

当预制外挂墙板的水平反力小于SEDC节点摩擦片的承载力Pf时,SEDC节点无相对滑移,呈现刚性节点的受力特性;当预制外挂墙板的水平反力超过SEDC节点摩擦片的承载力Pf时,SEDC节点可沿水平方向发生滑移,摩擦单元与弯曲单元协同工作,SEDC节点呈现柔性耗能节点的受力特性,预制外挂墙板可发生水平滑动以适应主体结构的变形,并耗散能量提高结构的抗震性能。

2 SEDC节点试验研究

2.1 试件设计

2.1.1 试件制作

以U形钢厚度t,U形钢高度h和预紧力Pc为研究参数,设计并制作了3组共9个SEDC试件,命名为SEDC-1～SEDC-9,3组试件分别进行单调加载、低周往复加载以及低周疲劳加载,以全面研究SEDC节点的受力机理、滞回特性与疲劳性能。各试件的弯曲单元(U形钢)尺寸如图3所示,U形钢采用激光切割与冷弯结合的方法制作,图中R为U形钢半径,l为U形钢平直段长度。大摩擦板与小摩擦板的几何尺寸如图4、5所示,试件的摩擦片采用NAO(无石棉有机摩擦材料),弯曲单元与摩擦单元的关键参数见表1。

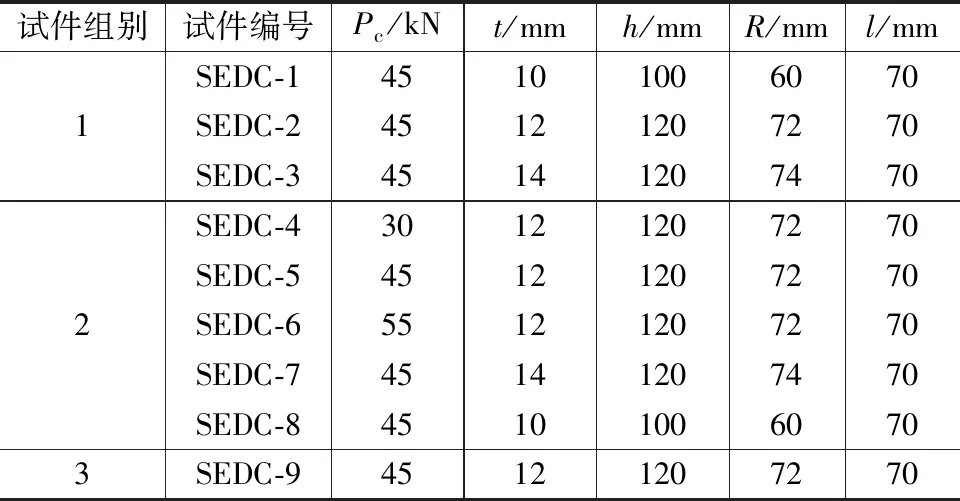
表1 试件详细参数

图3 U形钢几何尺寸

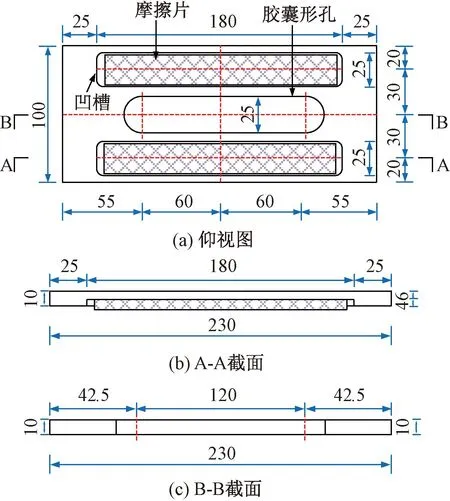
图4 大摩擦板几何尺寸

图5 小摩擦板几何尺寸

2.1.2 材料力学性能

本试验钢材采用Q235B级,按照《钢及钢产品力学性能试验取样位置及试样制备》(GB/T 2975—2018)[15]的要求对同批次钢板取样3组,并按照《金属材料 拉伸试验 第1部分:室温试验方法》(GB/T 228.1—2010)[16]进行材料受拉性能测试,所得的钢材力学性能见表2。

表2 钢材力学性能

为确定NAO摩擦片摩擦系数,设计了三明治式摩擦装置,如图6所示,该装置由内钢板、摩擦板、端固板、NAO摩擦片和高强螺栓组成。采用万能试验机对其进行单调位移加载试验,位移加载速率取0.5mm/s,初始预紧力取45kN,并采用力传感器全程记录预紧力变化情况,加载时下端固定,由上端作动器进行位移加载。

图6 摩擦装置图

NAO摩擦片的摩擦系数按式(2)计算[17]:

μ=f/nfPc

(2)

式中:μ为摩擦系数;f为摩擦力。

NAO摩擦片的摩擦力与预紧力随位移Δ变化曲线如图7所示。由图可知,试件的预紧力与摩擦力均呈现先增大后保持稳定的趋势,按照式(2)进行计算,NAO的摩擦系数取值为0.26。

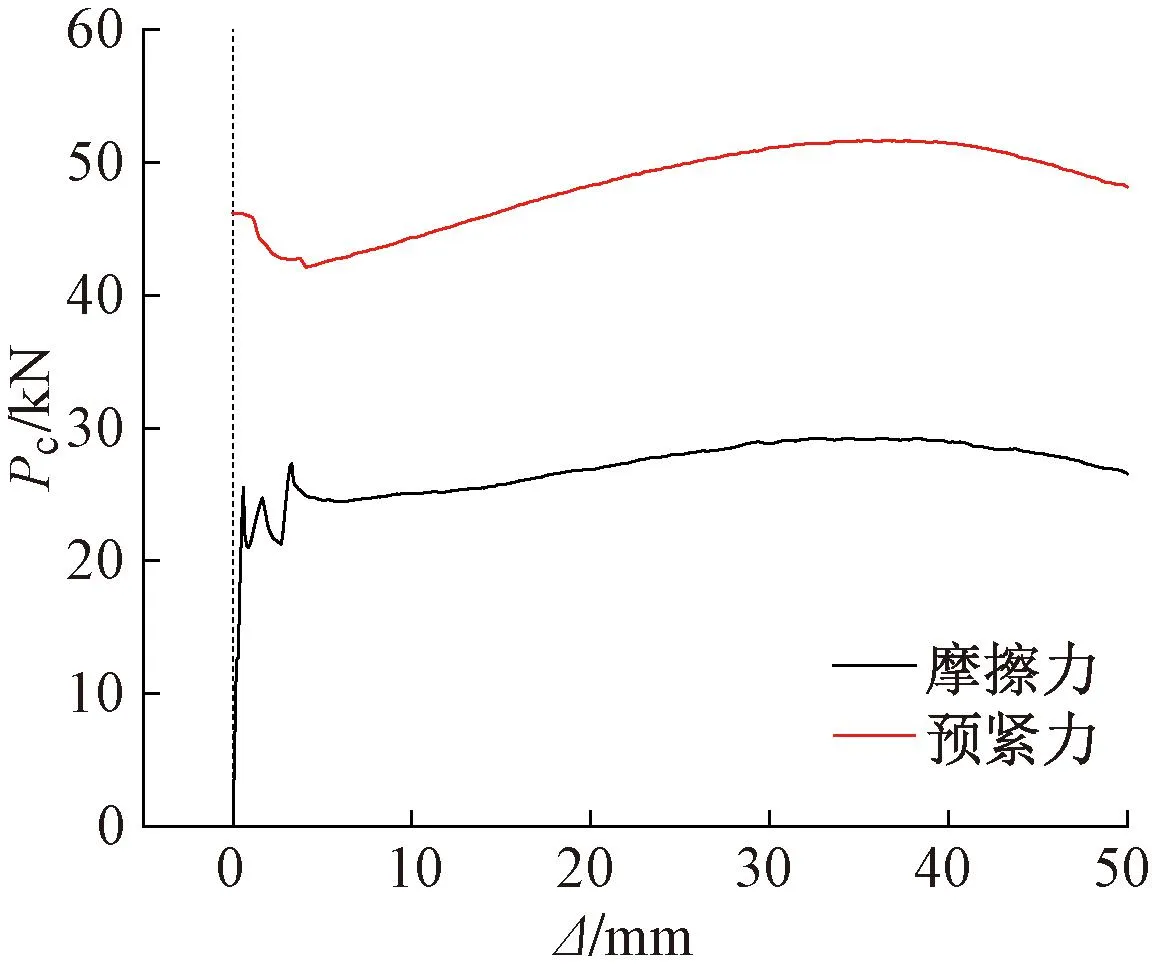
图7 预紧力与摩擦力随位移变化曲线

2.1.3 试验加载装置与加载制度

试验加载装置如图8所示,采用1 000kN的液压伺服作动器施加水平荷载,作动器的端部固定在反力墙上。试件安装在加载梁与侧向固定装置之间,液压伺服作动器仅能沿着滑轨的方向滑动,为了限制加载装置的面外变形,加载梁侧面设有面外限位装置,同时在限位装置与加载梁间涂抹黄油降低摩擦力。定义作动器向前推的方向为正向,作动器向后拉的方向为负向。

图8 试验加载装置

试件加载以位移角θ控制,如图2(b)所示,位移角θ按照式(3)计算:

θ=Δ/(2R+t)

(3)

式中Δ为加载位移。

单调加载制度的最大位移角为0.32;低周往复加载制度根据美国规范FEMA 461[18]确定,初始位移角θ0取0.0015,而后按照θi+1=1.4θi逐级加载,直至试件显著破坏或承载力下降至峰值承载力的85%以下时停止加载,低周往复加载制度如图9(a)所示;低周疲劳加载根据《建筑抗震设计规范》(GB 50011—2010)[19]确定,以0.234作为位移角幅值循环30次,低周疲劳加载制度如图9(b)所示。试件加载过程中的速率取值为0.5mm/s。

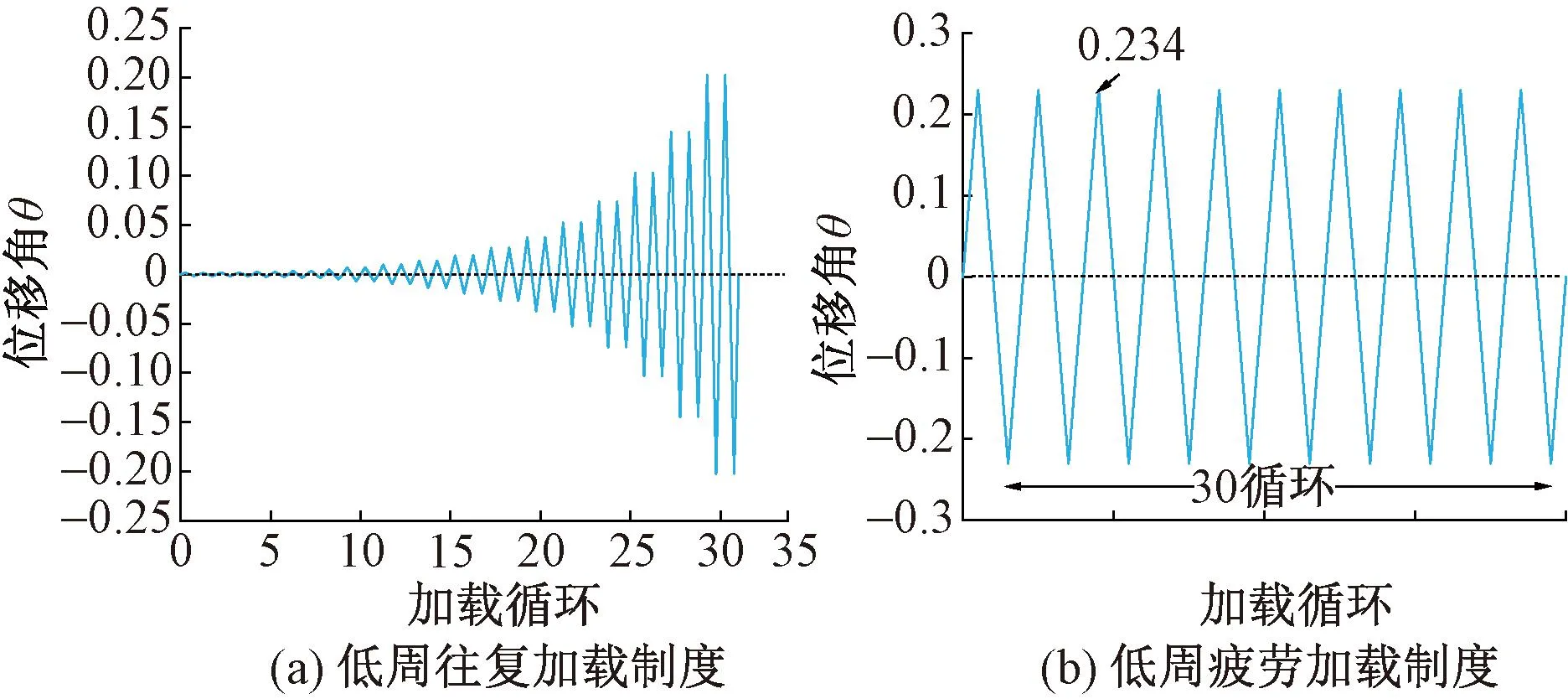
图9 加载制度

2.2 试验结果及分析

2.2.1 单调加载试验结果分析

(1)单调加载试验现象

试件SEDC-1～SEDC-3均采用NAO摩擦片,在试验中呈现出相似的现象,以试件SEDC-1为例进行说明,试验现象见图10。加载初期,荷载未超过试件SEDC-1的起始滑动荷载,试件SEDC-1保持静止,U形钢未出现变形;随着水平荷载的增大,大摩擦板与小摩擦板产生相对滑动变形,U形钢变形逐渐增大,加载至θ=0.085(位移11.5mm)时,NAO摩擦片滑动轨迹上留下较为清晰的白色轨迹;当加载至θ=0.2334(位移33.6mm)时,U形钢整体呈现履带式的变形模式,表面铁屑剥落,NAO摩擦片在摩擦作用下表面粉末不断剥落;当加载至θ=0.3267(位移47mm)时,U形钢表面没有裂缝出现,NAO摩擦片呈现颗粒状损伤模式,在预紧力集中区域,NAO摩擦片的损伤更为显著。

图10 试件SEDC-1试验现象

(2)荷载-位移曲线

试件SEDC-1～SEDC-3的荷载-位移(P-Δ)曲线如图11所示。由图可见,加载初期,试件的承载力近似呈垂直上升;继续加载,U形钢发生弹性变形,试件承载力增幅与位移增幅基本呈线性;随着加载位移继续增大,U形钢屈服,试件的承载力缓缓上升后趋于稳定,试件整体呈现显著的半刚性受力特性。在理想情况下,摩擦片的摩擦力保持稳定,同时,随加载位移增大,U形钢由弹性阶段进入弹塑性及塑性阶段,承载力逐渐增大而后趋于稳定,两者叠加下试件的承载力逐渐增大而后保持稳定;而各试件的承载力较早进入稳定阶段,原因在于各试件预紧力降低导致摩擦片摩擦力降低。

图11 单调加载下的荷载-位移曲线

试件SEDC-1～SEDC-3荷载、位移特征值见表3。由表3可见,随试件U形钢厚度增大,试件的初始刚度、屈服荷载及极限荷载逐渐增大,屈服位移减小。由式(1)计算可得各试件的起始滑动荷载理论值Pft为23.40kN,各试件起始滑动荷载的试验值与理论值吻合良好。

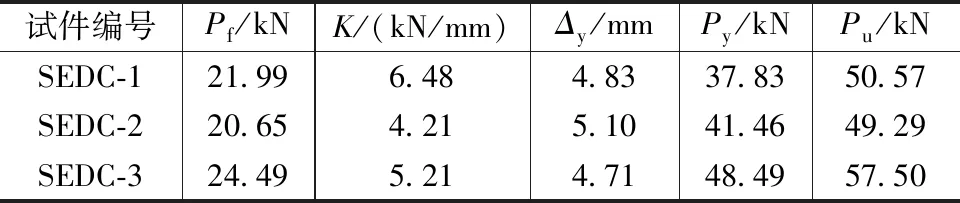
表3 试件SEDC-1～SEDC-3荷载、位移特征值

(3)应变分析

加载过程中试件SEDC-1的应变与位移的关系如图12所示,测点G-1、G-2为圆弧段与平直段节点处应变测点,测点G-3为圆弧段最外侧应变测点。由图可知,测点G-1处的应变显著高于测点G-2与测点G-3的应变,说明U形钢圆弧过渡段的变形较大,而圆弧段变形较小。测点G-1的应变低于测点G-2,原因在于底板约束了下侧U形钢平直段的变形。

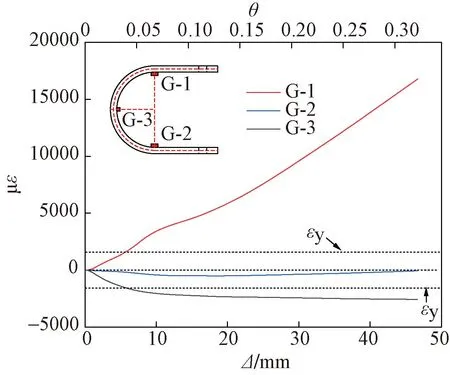
图12 试件SEDC-1应变发展规律

(4)预紧力分析

试件SEDC-1～SEDC-3在加载过程中预紧力Pc的变化规律如图13所示。由图可见,各试件的初始预紧力均为45kN,加载前期,各试件的预紧力整体呈现先增大后降低的趋势,前期预紧力上升的原因在于摩擦片与基础顶面不平行,在加载初期存在挤压效应,增大了预紧力Pc;而随加载位移增大,试件的摩擦片逐渐出现损伤,同时螺母出现松动,导致预紧力逐渐降低。加载结束时,试件SEDC-1～SEDC-3的预紧力降低幅度分别为18.71%、3.24%、14.31%,说明单调加载过程中,试件的预紧力能够保持稳定。

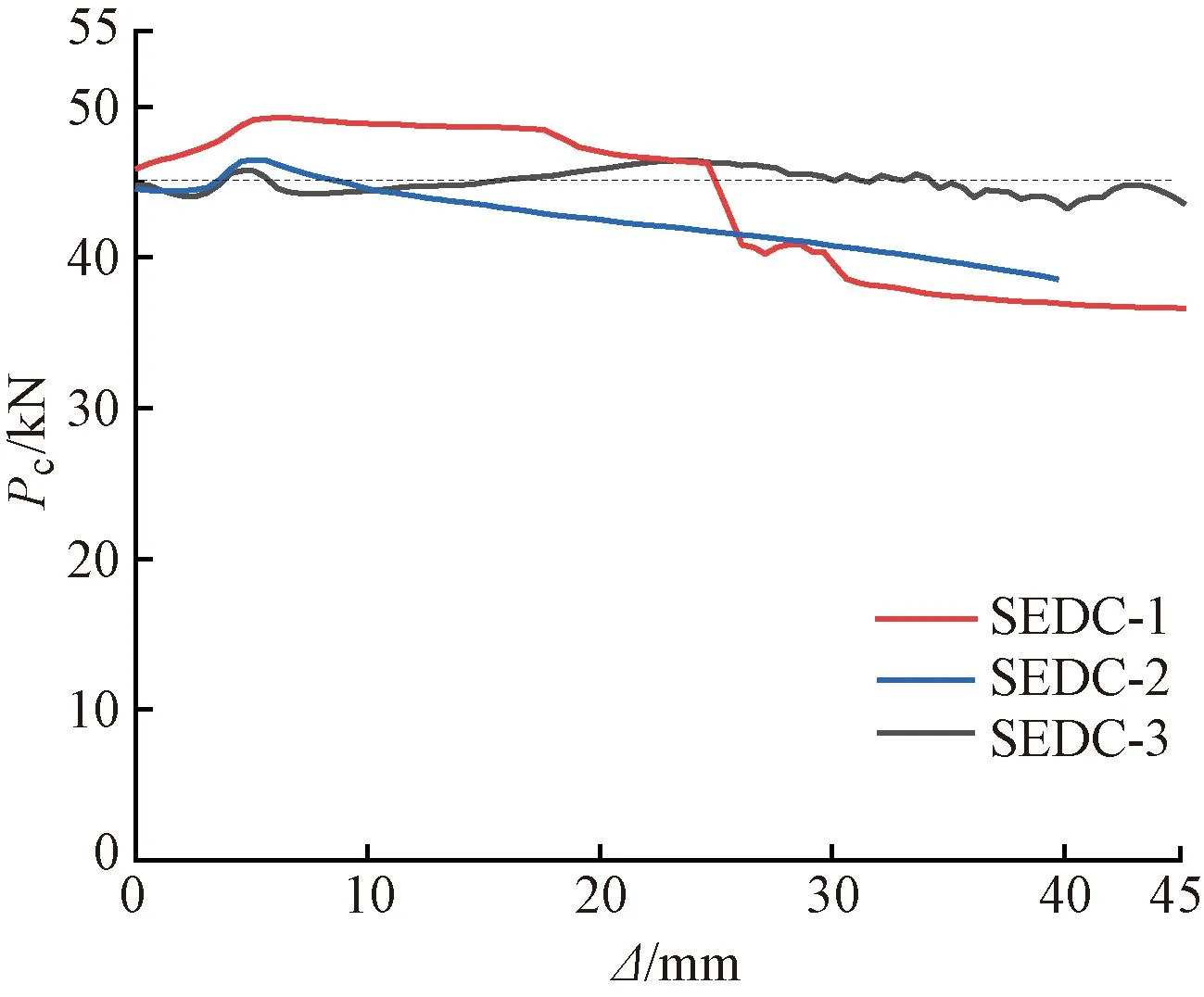
图13 预紧力变化规律

2.2.2 低周往复加载试验结果分析

(1)低周往复加载试验现象

试件SEDC-4～SEDC-8在低周往复荷载作用下呈现相似的现象,加载初期,试件保持静止,继续加载,大摩擦板开始滑动,当加载至θ=0.119(位移17.14mm)时,NAO摩擦片在其接触面上出现白色轨迹,U形钢表面氧化层脱落;当加载至θ=0.167(位移24.05mm)时,U形钢的履带式变形较为显著,NAO摩擦片出现颗粒状碎屑,摩擦片损伤逐渐累积;当加载至θ=0.327时,左侧U形钢平直段显著抬升,而右侧U形钢平直段与底板紧贴,U形钢呈现显著的履带式变形特征。加载结束后,U形钢表面未出现裂纹,NAO摩擦片呈现颗粒状损伤模式。试件SEDC-8在低周往复加载过程中的现象如图14所示。

图14 试件SEDC-8在低周往复加载过程中的现象

(2)滞回曲线

试件SEDC-4～SEDC-8的滞回曲线如图15所示。由图可见,各试件的滞回曲线较为相似,介于梭形与平行四边形之间。在正向加载与负向加载过程中,滞回曲线基本对称。当加载位移较小时,U形钢处于弹性阶段,滞回曲线近似呈线性发展,加载曲线与卸载曲线基本吻合,残余变形较小;随着加载位移的增大,U形钢逐渐屈服,试件承载力缓缓增加并逐渐趋于稳定,随着加载继续增大,NAO摩擦片损伤增大,摩擦系数减小,且高强螺栓螺母松动导致预紧力减小,试件承载力缓缓降低。各试件的滞回曲线均较为饱满,加载过程中U形钢与摩擦片呈现出较为良好的协同工作性能。

图15 低周往复加载下的试件滞回曲线

(3)骨架曲线

试件SEDC-4～SEDC-8的骨架曲线如图16所示。由图可见,试件的骨架曲线呈现显著的半刚性受力特性。加载前期,试件的承载力近似呈垂直增大,继续加载,试件开始滑动,此时U形钢处于弹性阶段,NAO摩擦片基本没有损伤,试件的承载力上升较快;而后U形钢屈服进入弹塑性阶段,试件的承载力缓缓增大至峰值并趋于稳定;继续加载,摩擦片的损伤逐渐累积,摩擦系数减小,同时螺母松动导致预紧力逐渐损失,试件的承载力略微下降。

图16 低周往复加载下的试件骨架曲线

试件SEDC-4～SEDC-8的荷载、位移特征值见表4。由表可见,随着预紧力的增大,试件的起始滑动荷载P0、屈服荷载Py、峰值荷载Pm、极限荷载Pu增大,屈服位移Δy基本不变;随着U形钢厚度的增大,试件起始滑动荷载P0、屈服荷载Py、峰值荷载Pm、极限荷载Pu增大,屈服位移Δy减小。

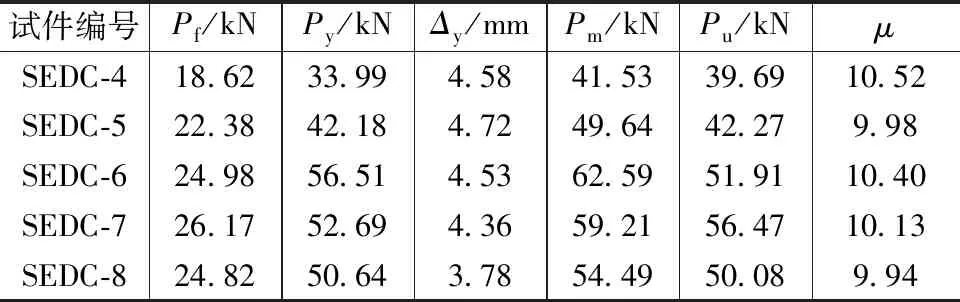
表4 试件SEDC-4～SEDC-8的荷载、位移特征值

(4)刚度退化

以试件的割线刚度Ki衡量试件的刚度退化情况,按照式(4)计算:

(4)

试件SEDC-4～SEDC-8刚度退化如图17所示。由图可见,加载初期,试件刚度退化速度较快,随着加载位移增大,U形钢逐渐屈服,NAO摩擦片损伤逐渐累积,试件刚度退化速度逐渐降低并逐渐趋于稳定。试件在加载过程中的刚度退化较为稳定,没有出现刚度突变现象,U形钢与NAO摩擦片整体呈现较为良好的协同工作性能。

图17 试件SEDC-4～SEDC-8刚度退化曲线

(5)耗能能力

试件滞回环面积(Ed)和等效黏滞阻尼系数(he)常被用来衡量试件或结构在地震作用下的耗能能力,其中等效黏滞阻尼系数按照式(5)计算:

(5)

式中:Ed为试件滞回曲线的面积;SΔOBE和SΔODF为分别对应于正向与负向上的最大承载力与最大水平位移围成的三角形面积,如图18所示。

图18 等效黏滞阻尼系数he

试件SEDC-4～SEDC-8的耗能能力如图19(a)所示。由图可见,在弹性阶段,U形钢处于弹性阶段,仅依靠摩擦单元耗能,试件的耗能较小;随加载位移增大,U形钢进入弹塑性阶段,耗能显著增大。在加载结束时,试件的弯曲单元与摩擦单元均未破坏,耗能仍具有稳定的上升空间。随摩擦单元预紧力的提高以及弯曲单元U形钢厚度的增大,节点的耗能逐渐增大。

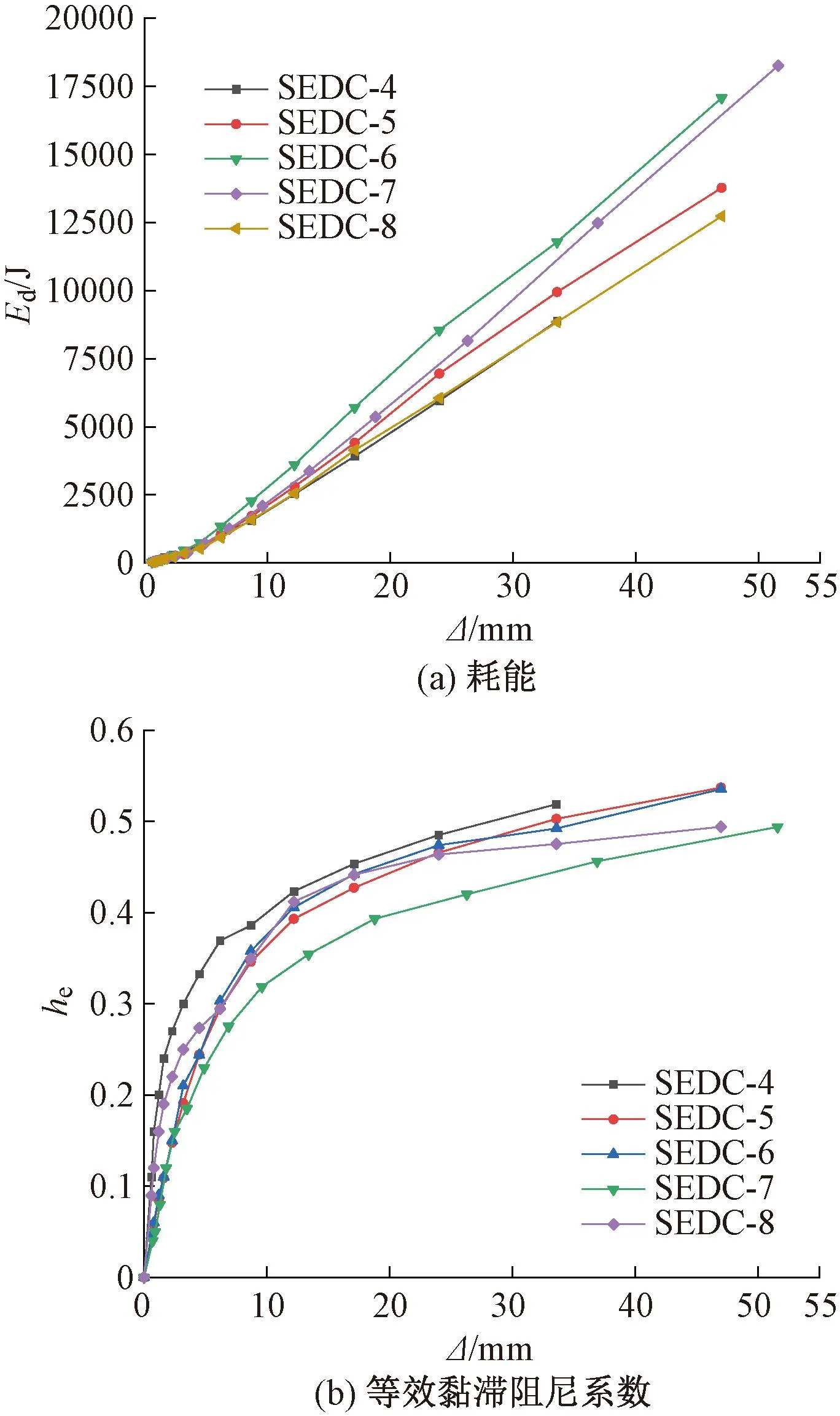
图19 试件SEDC-4～SEDC-8的耗能能力

试件SEDC-4～SEDC-8等效黏滞阻尼系数如图19(b)所示。由图可见,加载位移较小时,摩擦单元的耗能能力较为稳定,耗能与理想耗能的比值较高,等效黏滞阻尼系数前期提升较快;随着加载位移的增大,U形钢的耗能占比提高,等效黏滞阻尼系数上升的速度降低,最大值在0.5～0.6之间,体现了优越的耗能能力。

(6)延性

延性系数μ按照式(6)计算[20]:

μ=Δu/Δy

(6)

式中:μ为延性系数;Δu与Δy分别为试件极限位移与屈服位移。

按照式(5)计算的试件延性系数见表4。由表可见,各试件的延性系数均大于8,表明该节点具有良好的变形能力,在地震作用下能够协调预制外挂墙板与主体结构的相对变形,防止预制外挂墙板脱落。随U形钢厚度增大,试件屈服位移降低,而极限位移保持稳定,延性系数降低。随预紧力增大,试件屈服位移与极限位移均保持稳定,因此延性系数保持不变。

(7)应变分析

试件SEDC-5、SEDC-7加载过程中U形钢关键测点的应变如图20所示。由图可见,各测点的应变随位移增大逐渐增加,测点G-1、G-2处的应变显著高于测点G-3处的应变,说明U形钢圆弧过渡段的变形显著高于其圆弧段;测点G-1的应变低于测点G-2,原因在于底板约束了下侧U形钢平直段的变形。

图20 试件SEDC-5、SEDC-7应变-位移曲线

(8)预紧力分析

试件SEDC-5、SEDC-7、SEDC-8加载过程中的预紧力如图21所示,其初始预紧力均为45kN,加载过程中预紧力的峰值见表5。由图21、表5可知,加载初期由于试件与加载装置存在加工误差,以及加载装置间存在挤压效应,试件的预紧力变化较为显著。随着加载位移继续增大,NAO摩擦片损伤逐渐累积,摩擦系数略微降低,同时加载过程中螺母逐渐松动导致试件预紧力损失。各试件的预紧力变化范围均在初始预紧力的20%以内,能够保持稳定。在工程应用中,可考虑采用多个螺栓施加预紧力以降低预紧力损失。

表5 试件预紧力变化情况

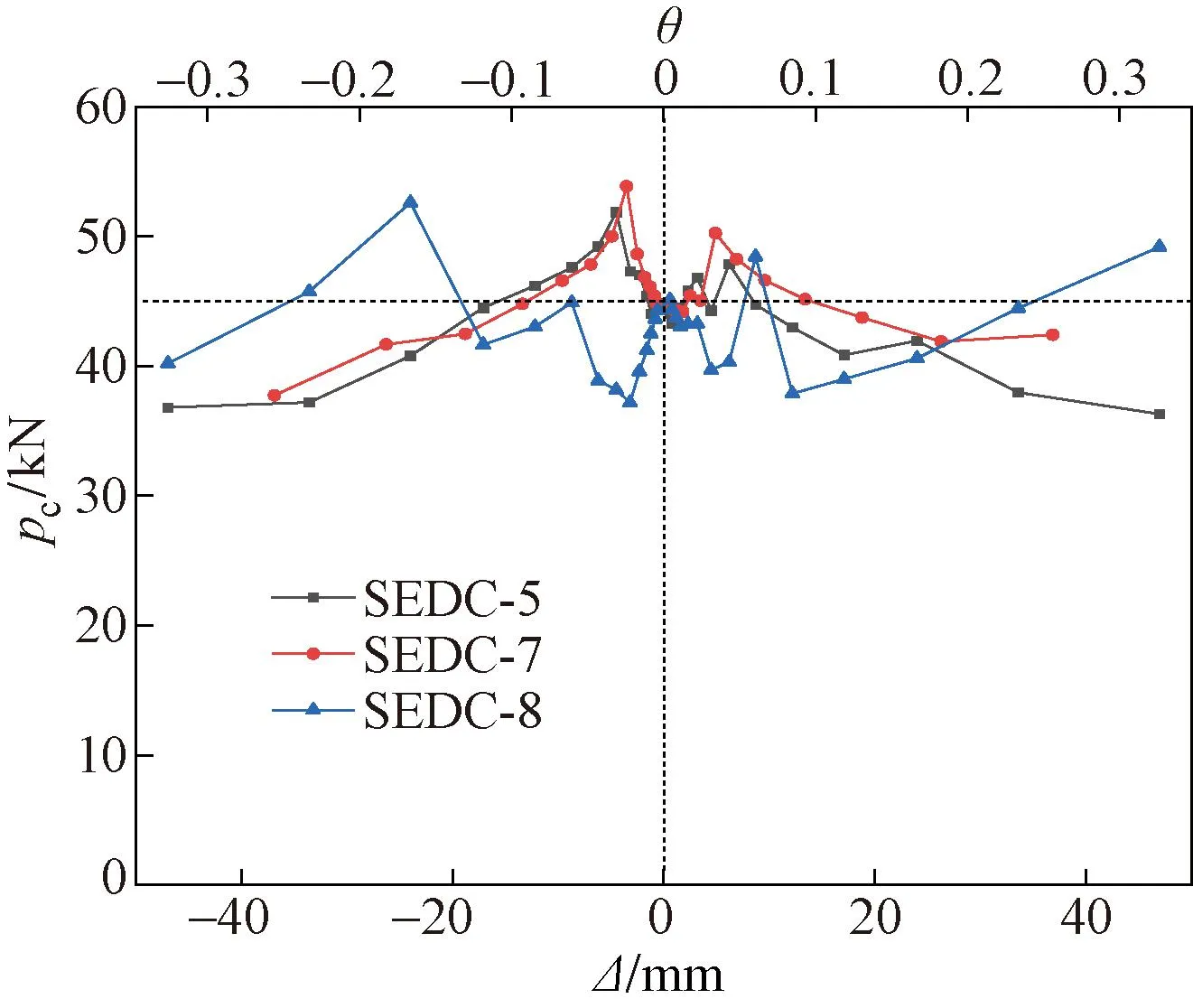
图21 预紧力-位移曲线

2.2.3 低周疲劳试验结果分析

(1)低周疲劳试验现象

低周疲劳加载过程中的试验现象与低周往复加载现象基本一致。随加载位移的增大,U形钢由弹性进入弹塑性阶段,呈现履带式变形,残余变形逐渐增大,但表面未出现裂纹;NAO摩擦片在加载过程中损伤逐渐累积,摩擦片碎屑不断脱落,呈现颗粒状损伤。试件SEDC-9低周疲劳加载过程中的现象及破坏模式如图22所示。

图22 低周疲劳试验现象

低周疲劳加载结束后,小摩擦板的损伤更为显著,原因在于其摩擦接触面较小,轴向应力较大。大摩擦板的摩擦片接触面较大,损伤程度整体较低,但由于预紧力的不均匀分布,其一侧NAO摩擦片断裂为三段。

(2)低周疲劳荷载-位移曲线

试件SEDC-9在低周疲劳荷载作用下的荷载-位移曲线如图23所示。由图可见,随循环加载次数增大,试件的承载力逐渐降低。加载至第1圈时,试件的正向与负向峰值承载力分别为53.47kN与45.16kN,当加载至第30圈时,试件SEDC-9正向峰值承载力较初始值降低了16.81kN,下降幅度为33.31%,负向峰值承载力较初始值降低了11.44kN,下降幅度为25.33%,试件SEDC-9在低周疲劳荷载作用下的承载力下降幅度显著,原因在于NAO摩擦片摩擦损伤较大,且部分摩擦片断裂。应采用增大摩擦片接触面以及增加螺母数量等措施,降低摩擦片、预紧力的损失,提高试件低周疲劳性能。

图23 试件SEDC-9的荷载-位移曲线

3 数值分析

本文采用ABAQUS建立SEDC的数值模型,基于试验结果验证建模方法的准确性,在此基础上分析弯曲单元与摩擦单元设计参数对SEDC受力性能的影响,为SEDC的应用提供参考。

3.1 数值模拟验证

3.1.1 数值模拟模型建立

(1)钢材本构关系

钢材采用Q235B钢,采用双折线强化材料本构模型,材料具体参数根据前述材性试验确定,高强螺栓在加载过程中未出现显著的变形,因此采用弹性本构模型。

(2)单元选取及接触设置

SEDC数值模型中的钢板及螺栓均采用八节点六面体线性减缩积分(C3D8R)单元,由于NAO摩擦片在加载过程中的轴向变形较小,通过模型收敛性分析,将NAO-钢接触面简化为钢-钢接触面,其法向采用硬接触,切向采用罚函数,摩擦系数取0.26。高强螺栓与钢板孔壁间采用硬接触,高强螺栓的预紧力通过螺栓荷载施加。将加劲肋及摩擦板与墙板预埋件合并为整体以模拟焊接连接,数值模型的单元尺寸取值为5mm。采用上述建模方法建立的数值分析模型如图24所示。

图24 SEDC数值分析模型

(3)边界条件与加载方式

根据SEDC试件的约束条件,约束数值模型主体结构预埋件6个方向的自由度以模拟固定支座,墙板预埋件仅保留加载方向(X向)的平动自由度,其余方向自由度均进行约束。SEDC数值模型分两步加载,第一步施加螺栓的预紧力以及模型的边界条件,第二步进行水平位移加载。数值模型的加载制度与试验的加载制度保持一致。

3.1.2 数值结果验证

(1)单调加载工况

采用上述建模方法,建立了试件SEDC-1的数值分析模型,数值模拟结果与试验结果如图25所示,关键参数对比见表6。由图25、表6可见,数值模拟与试验结果的荷载-位移曲线呈现相似的发展规律,其数值模拟与试验结果的起始滑动荷载Pf与极限荷载Pu的平均相对误差分别为7.85%与4.09%,单调加载工况下数值模拟结果与试验结果吻合良好。

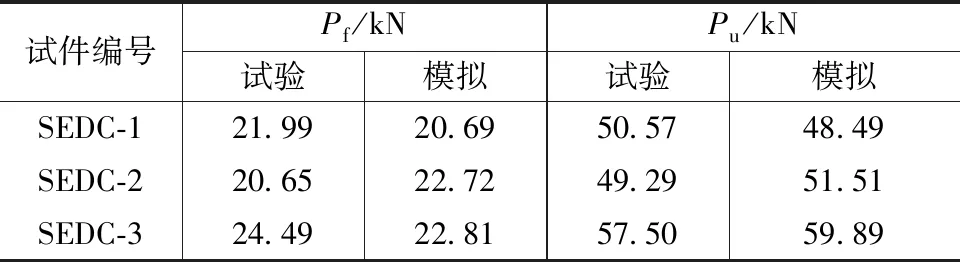
表6 单调荷载数值模拟结果与试验结果对比

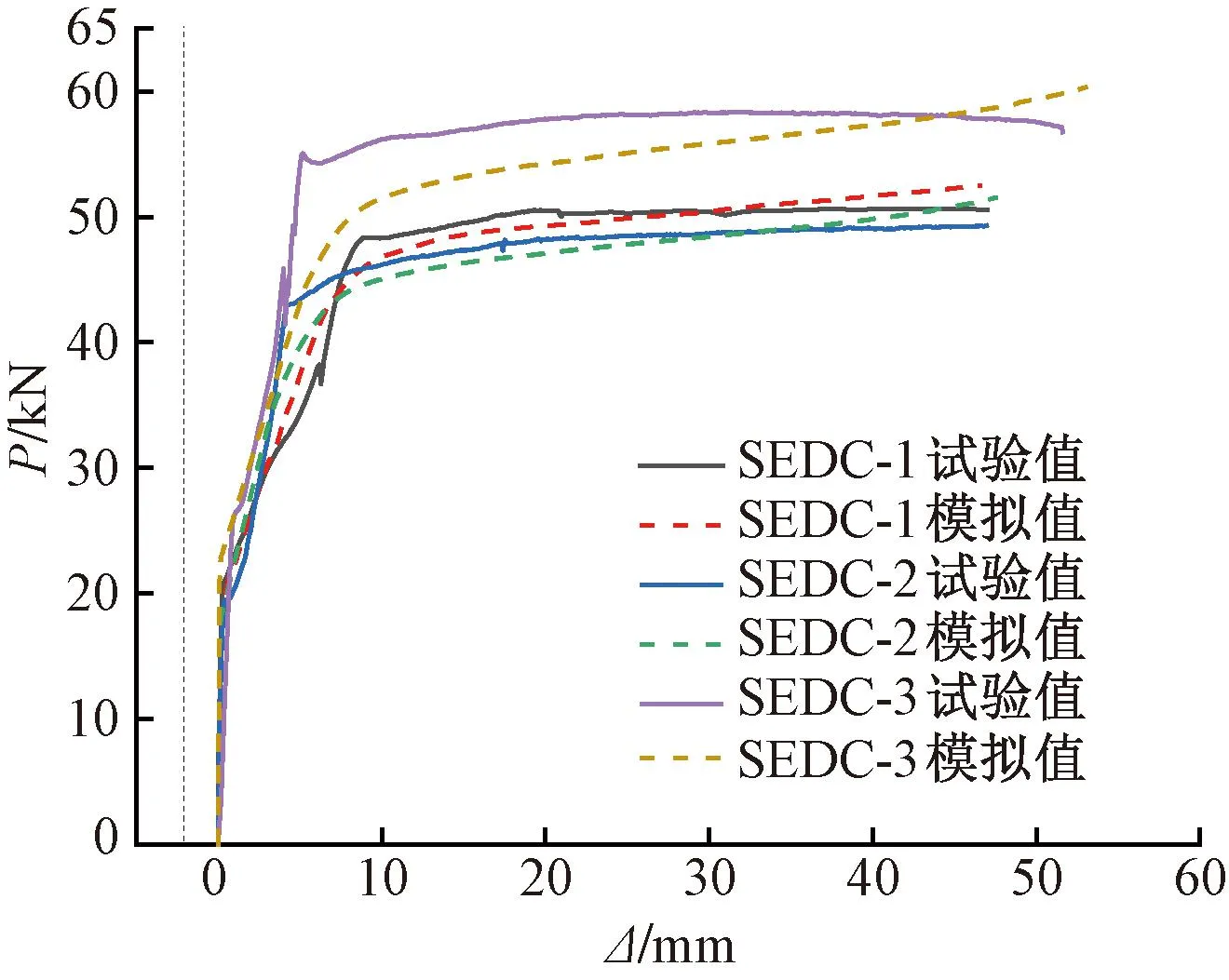
图25 数值模拟结果与试验结果对比

(2)低周往复加载工况

采用上述建模方法,建立了试件SEDC-5与试件SEDC-6的数值分析模型,低周往复荷载作用下数值模拟结果与试验结果滞回曲线对比如图26所示。由图可见,数值模拟结果的滞回曲线与试验滞回曲线吻合良好。数值模拟结果刚度及承载力均略高于试验结果,原因在于数值模型未考虑加载装置间的误差,以及材料力学性能的不均匀等因素。

图26 试件SEDC-5、SEDC-6滞回曲线对比

3.2 参数分析

基于上述建模方法,设计并建立了12组数值分析模型,分析U形钢平直段长度L、U形钢宽度B、预紧力等参数对SEDC受力性能的影响。各数值分析模型的关键参数见表7,其中Basic试件为基础对比试件,其设计参数与试件SEDC-2相同。

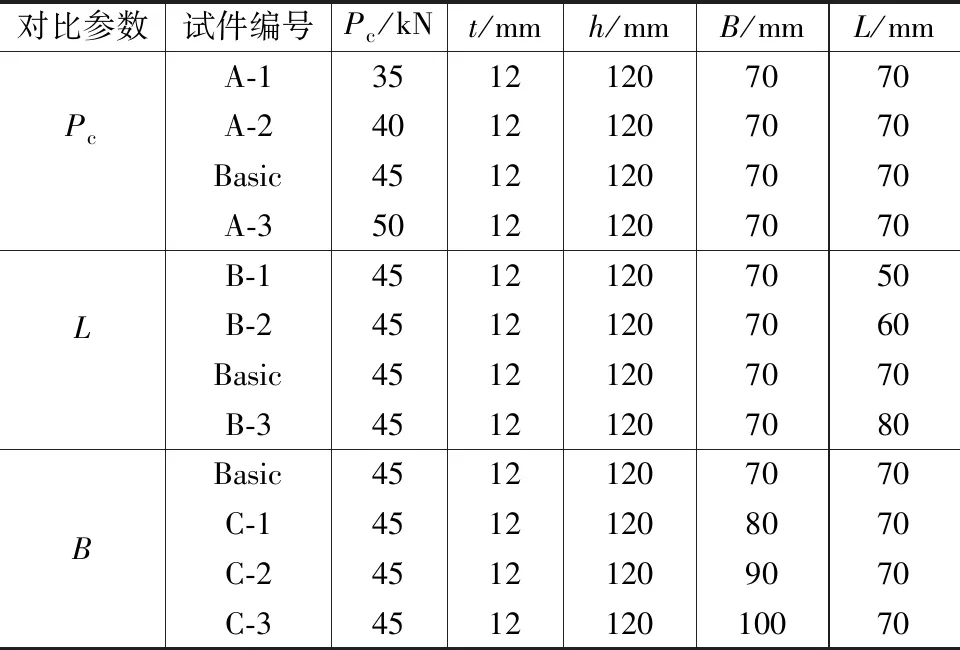
表7 分析参数

不同参数分析试件数值模型的计算结果如图27所示,其荷载、位移特征值见表8。由图27、表8可见,(a)所示,随预紧力增大,试件弹性刚度、起始滑动荷载、屈服荷载、极限荷载显著增大,屈服位移基本保持不变。随U形钢平直段长度增大,试件弹性刚度、屈服荷载、极限荷载逐渐降低,屈服位移减小。随U形钢宽度增大,试件弹性刚度、屈服荷载、极限荷载逐渐增大,屈服位移逐渐降低。对比各设计参数,U形钢宽度以及预紧力对SEDC的影响较为显著,可通过合理控制其设计值以满足不同预制墙板的设计需求。

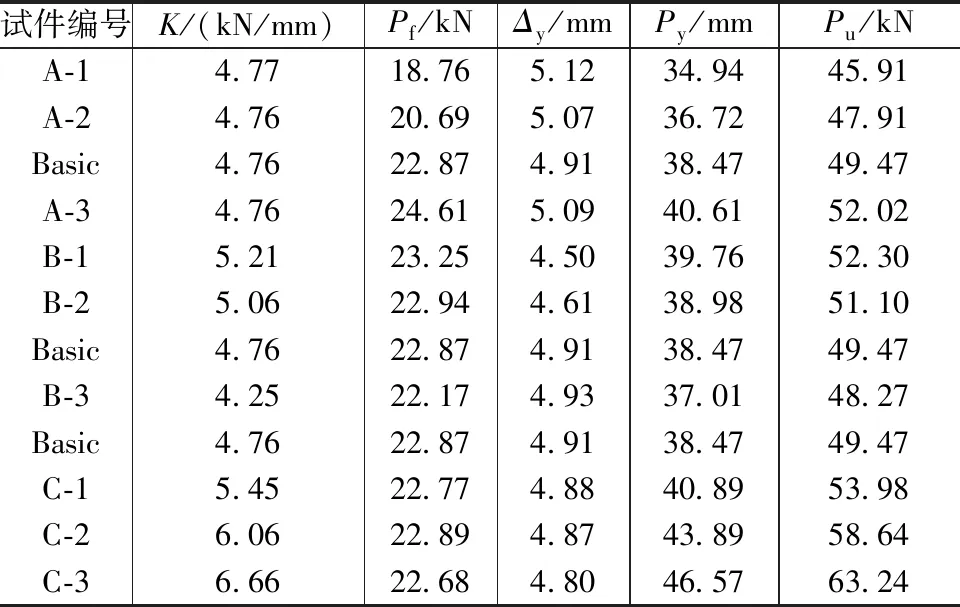
表8 各试件荷载、位移特征值

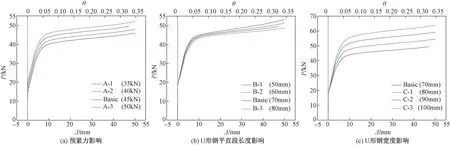
图27 不同参数分析试件的荷载-位移曲线

4 SEDC设计方法研究

根据《预制混凝土外挂墙板应用技术标准》(JGJ/T 458—2018)[3],预制外挂墙板的受力如图28所示。

图28 预制外挂墙板受力简图

在重力荷载G作用下,预制外挂墙板的节点反力计算示意图如图29所示,其面内竖向节点反力Rvn与Rvp可按照式(7)计算:

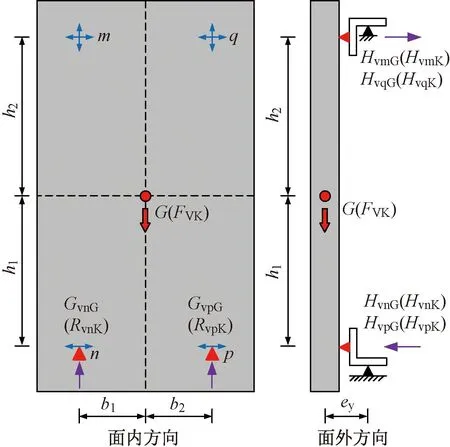
图29 重力荷载及竖向地震作用下预制外挂墙板计算简图

Rvn=Rvp=G/2

(7)

其面外节点反力Hvn、Hvp、Hvm与Hvq可按照式(8)计算:

(8)

式中:ey为偏心距;h1为预制外挂墙板重心至SEDC节点的竖向间距;h2为预制外挂墙板重心至上部节点的竖向间距。

预制墙板的水平地震力FEK按照式(9)计算[3]:

FEK=βEαmaxG

(9)

式中:βE为地震作用动力放大系数;αmax为水平地震影响系数最大值;G为墙板重力荷载设计值。

在水平地震作用下,预制外挂墙板的节点反力计算示意图如图30所示。其面内水平节点反力Hhn与Hhp可按照式(10)计算:

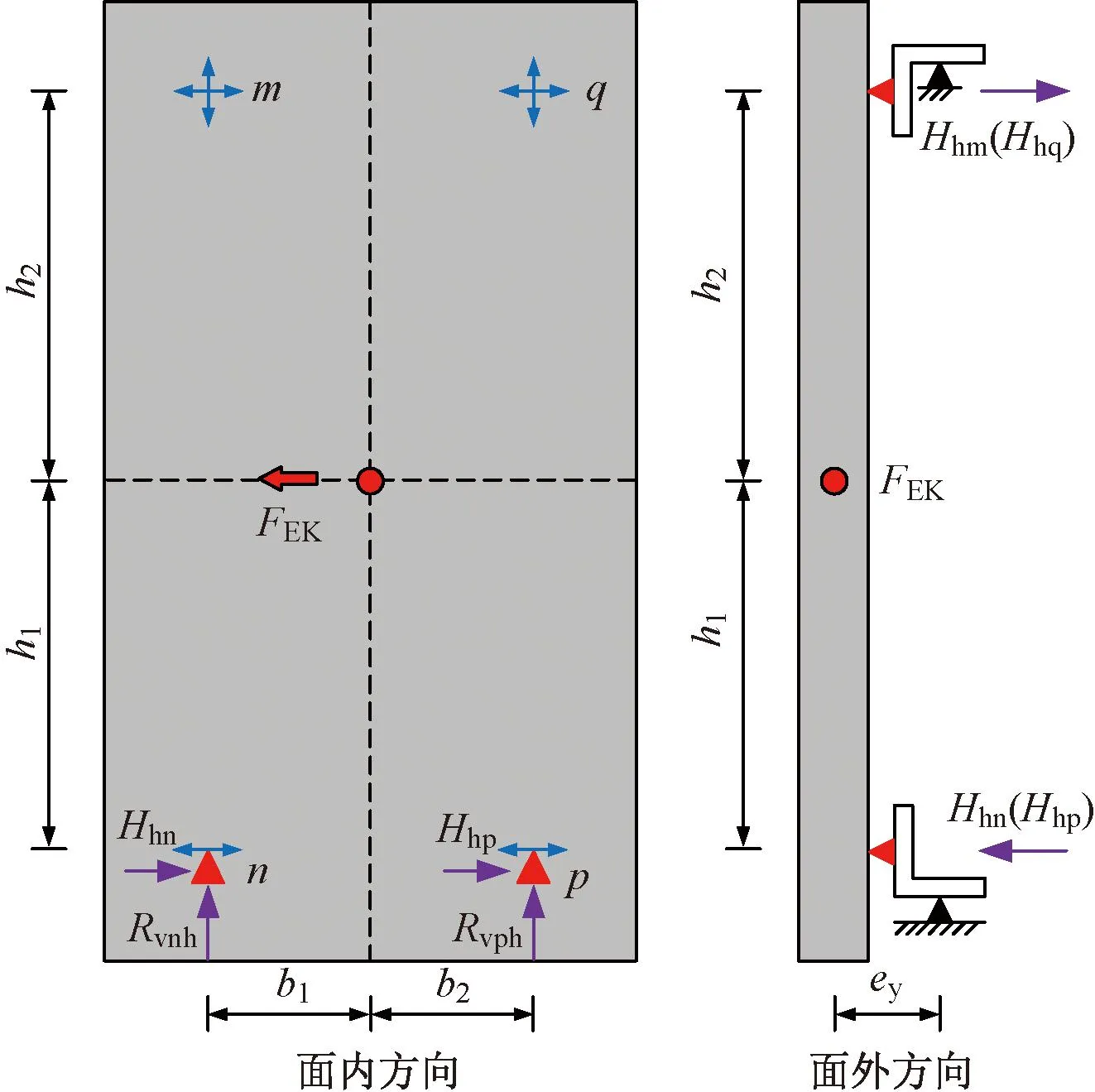
图30 水平地震作用下预制外挂墙板计算简图

Hhn=Hhp=FEK/2

(10)

其面内竖向节点反力Rvnh与Rvph可按照式(11)计算:

Rvnh=Rvph=FEKh1/2b1

(11)

式中b1为预制外挂墙板重心至SEDC节点的水平间距。

其面外水平节点反力Hhn、Hhp、Hhm及Hhq可按式(12)、(13)计算:

(12)

(13)

预制外挂墙板的风荷载W按照式(14)计算:

W=βzμsμzω0

(14)

式中:βz为风振系数;μs为风荷载体型系数;μz为风压高度变化系数;ω0为基本风压。

在风荷载作用下,预制外挂墙板的节点反力计算简图如图31所示。其面外水平节点反力Hhnw、Hhpw、Hhmw及Hhqw可按照式(15)、(16)计算:

(15)

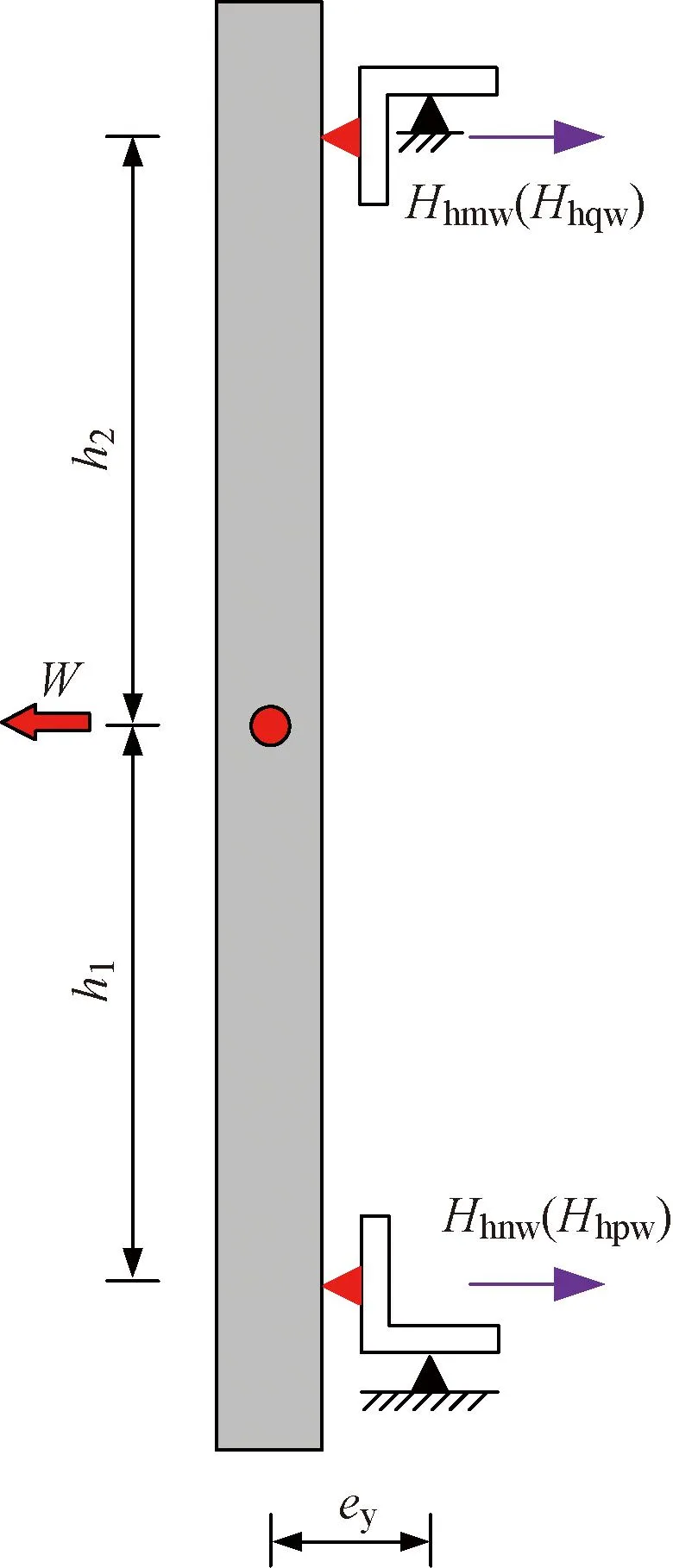
图31 风荷载作用下预制外挂墙板计算简图

(16)

在竖向地震力FVK作用下,预制外挂墙板的节点反力计算示意图如图29所示,预制外挂墙板的竖向地震力FVK按照式(17)计算:

FVK=0.65FEK

(17)

在竖向地震作用下节点竖向反力RvnK与RvpK可按式(18)计算:

RvnK=RvpK=FVK/2

(18)

其面外节点反力Hvn、Hvp、Hvm与Hvq可按照式(19)计算:

(19)

在正常使用阶段,SEDC节点在风荷载与重力荷载作用下的最大水平力Hwg可按式(20)计算:

(20)

在此阶段预制外挂墙板与主体结构应保持刚性连接,则SEDC节点的起始滑动荷载Pf应满足式(21):

Pf≥Hwg

(21)

在地震作用下,预制外挂墙板与主体结构由刚性连接转化为柔性耗能连接,则SEDC节点起始滑动荷载Pf应满足式(22):

(22)

式中n为SEDC的数量。

因此,为实现预制外挂墙板与主体结构正常使用阶段的刚性连接以及地震作用下的柔性连接,SEDC节点的预紧力Pf应满足:

(23)

5 结论

(1)SEDC具有显著的半刚性受力特征,其受力可分为静摩擦阶段与滑动摩擦阶段,两阶段的临界荷载通过预紧力与摩擦板摩擦系数控制。在单调加载与低周往复加载过程中,各SEDC的U形钢均呈现履带式的变形特征,NAO摩擦片呈现颗粒状损伤模式。

(2)SEDC的金属弯曲耗能元件与摩擦耗能元件具有良好的协同工作能力,其滞回曲线饱满,承载性能稳定,变形性能与耗能能力优越。随着U形钢厚度的增大,SEDC的承载力与耗能能力提高,屈服位移减小;随着预紧力的增大,SEDC的承载力与耗能能力提高,起始滑动荷载增大。

(3)SEDC数值模拟结果与试验结果吻合良好。数值模拟结果表明随U形钢宽度增大,SEDC的承载力与刚度增大,而屈服位移基本不变;随着U形钢平直段长度增大,SEDC的承载力与刚度降低,而屈服位移提高。

(4)基于预制外挂墙板点支承连接方式的变形特征及其在各工况下的节点反力,并结合SEDC的半刚性受力特性,提出了基于SEDC的预制墙板与主体结构的协调设计方法。