八点弹性不均匀支承的类椭圆形弦支穹顶结构设计与分析研究

汤凯峰, 赵文雁, 潘文智, 陈兆弘

(1 筑博设计股份有限公司，深圳 518042；2 浙江精工钢结构集团有限公司，绍兴 312030)

0 引言

弦支穹顶结构为由上部刚性网壳与下部柔性索杆体系组合而成的刚柔相济的杂交结构体系[1-4]。随着结构造型及功能的日益复杂,弦支穹顶壳面从传统的球面[5]、椭球面[6]、椭圆抛物面[7]发展到异形的曲面[8],支承方式从连续支承、不连续支承发展到不连续弹性支承,甚至网壳局部区域存在较大的不均匀荷载。

对于上述复杂弦支穹顶,其结构设计主要存在以下两方面的特点:

一方面,常规弦支穹顶均直接由下部混凝土结构支承,可简化为刚性支承,而对于不连续弹性支承的弦支穹顶,由于其结构支承条件的复杂性,其支承条件对结构受力及变形的影响需进行充分考虑。

另一方面,在网壳刚度、撑杆上节点不同标高、荷载等不规则分布的情况下,传统的同一圈撑杆等长度的布索形式是否仍然具有合理性,是个值得深思的问题。撑杆长度与各圈径向索与水平面间的夹角直接相关,角度越大撑杆越长,随着撑杆长度的增大,网壳的竖向位移减小,能有效降低上部杆件和下部拉索的内力峰值,但撑杆长度增加到一定程度后上述效果就不再明显,说明撑杆长度存在一个合理的取值,撑杆过长时还需要考虑撑杆的稳定性[9]。国内部分学者也对弦支穹顶结构的布索形式(撑杆的长度分布)进行了相关研究[9-15],提出了马鞍形、阶梯形等布索形式,马鞍形布索形式能有效地调节类椭圆形弦支穹顶结构长短轴网壳的刚度差值,使得结构的变形及内力分布更为均匀,但其在异形弦支穹顶中的适用性仍需进一步研究。

针对异形壳面、不均匀弹性支承、荷载不均匀分布等复杂条件下弦支穹顶结构的设计问题,本文以大沙河文体中心会议厅八点弹性不均匀支承类椭圆形弦支穹顶为例,剖析其结构设计思路及特点,对其弹性支承条件的影响进行对比研究,并结合基于刚性索法和改进PGSA算法的预应力优化方法,对不同布索形式下的弦支穹顶结构进行静力及稳定性能的对比分析。

1 工程概况

大沙河文体中心项目位于深圳市南山区,总用地面积为41968.97m2,规划建设包括了体育运动类用房、文化类用房、配套商业用房等。项目整体(图1(a))平面投影呈矩形,长方向约195m,短方向约120m,最高点标高为52m。其中,顶层城市客厅屋盖为异形曲面,其平面投影为类椭圆形,长轴跨度为50.4m,短轴跨度为42m,矢高为5.4m。

图1 大沙河文体中心项目整体效果图及结构模型轴测图

2 结构设计

根据建筑屋面形态,结合下部结构的支承条件,并综合考虑各结构体系的适用性,项目城市客厅屋盖采用肋环型单层网壳+Giger型索系组成的类椭圆形弦支穹顶结构体系。大沙河文体中心整体结构模型如图1(b)所示。

2.1 结构设计重难点

(1)八点弹性不均匀支承

常规的弦支穹顶直接由下部混凝土结构支承,可简化为刚性支承。而本项目弦支穹顶结构由下部8根钢柱作为支承,钢柱又由下方58.8m的大跨度桁架支承(图2、3),长、短轴方向钢柱落点不同,导致桁架对8根钢柱的支承刚度不一致,此外存在两根钢柱同时落在同一榀桁架的情况,结构支承条件较为复杂,对外圈环桁架结构的刚度提出了较高的要求,设计过程中需评估支承条件对结构受力及变形的影响。

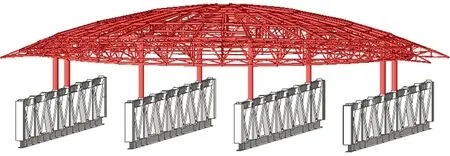
图2 弦支穹顶

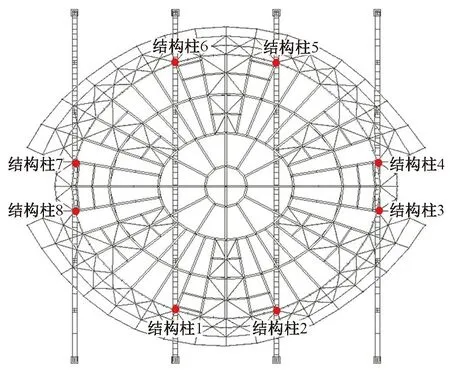
图3 弦支穹顶平面布置图

(2)荷载不均匀分布

除常规的均布恒、活荷载外,屋盖正交方向上布置有220kN的水箱荷载(共8个),此外还需考虑主体结构屋面与弦支穹顶之间的荷载传递,即屋面构件搭接(图4红框处)荷载,这对局部结构的变形及受力有较大的影响。

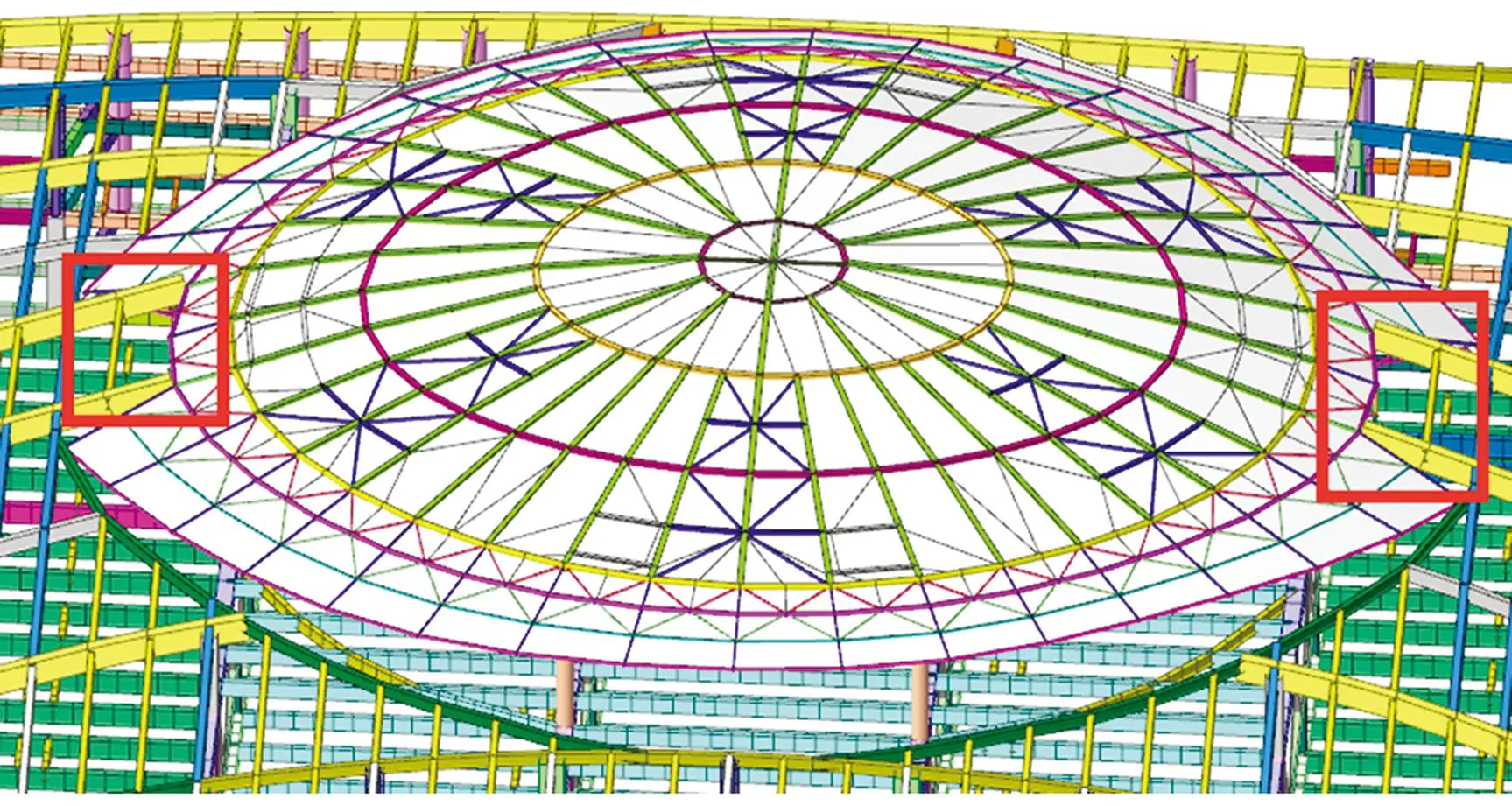
图4 屋面构件搭接

(3)异形壳面

屋盖为异形壳面,其投影为类椭圆形。若按常规弦支穹顶的节点分布特点,将同一圈环向节点处于同一标高(图5),受异形曲面的影响,同一圈径向杆的长度会相差较大,长、短轴方向最外圈径向杆最大相差3.5m,造成最外圈径向索的索长以及与水平面的夹角相差较大,大大影响了索杆体系对上部网壳的支承刚度。

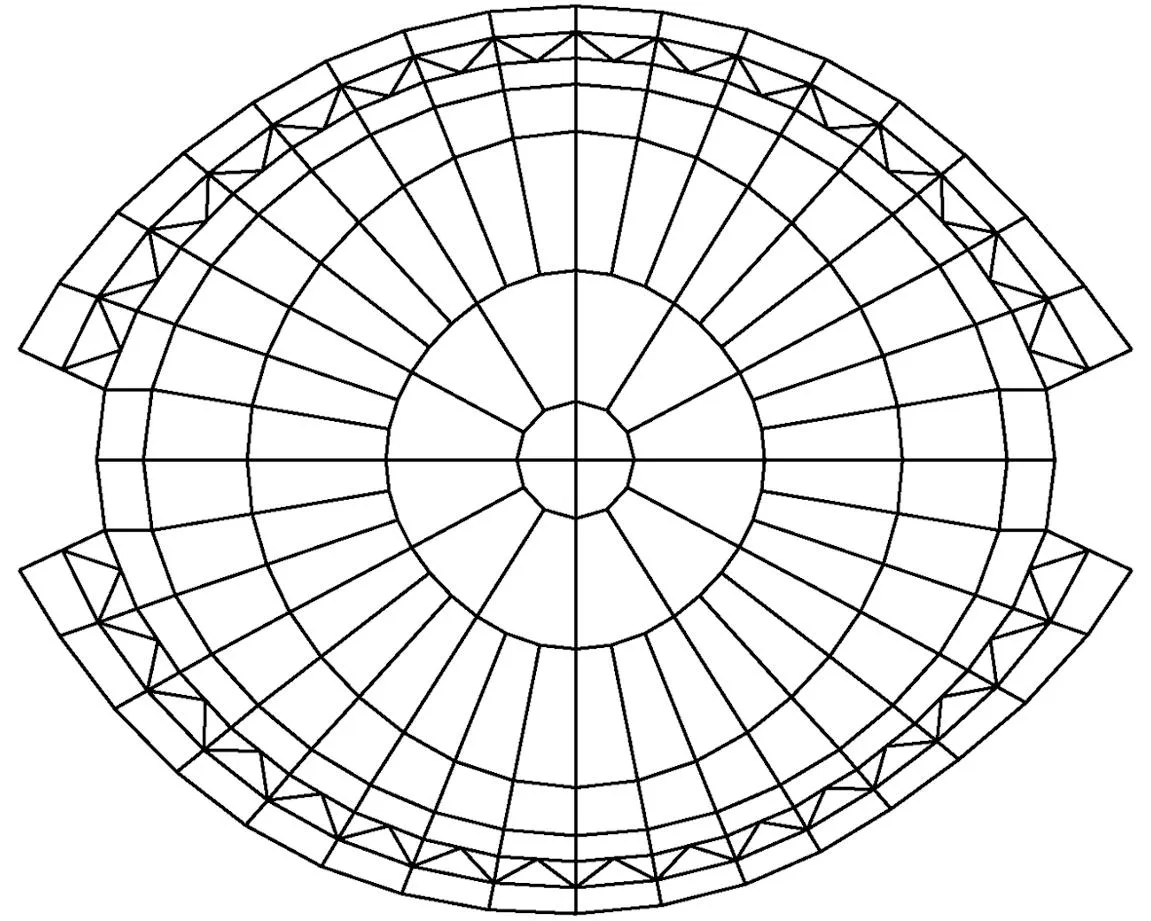
图5 按同一圈环向节点处于同一标高生成的网壳

2.2 结构设计概况

弦支穹顶结构组成如图6所示。其各组成部分设计情况及构件材质如下:

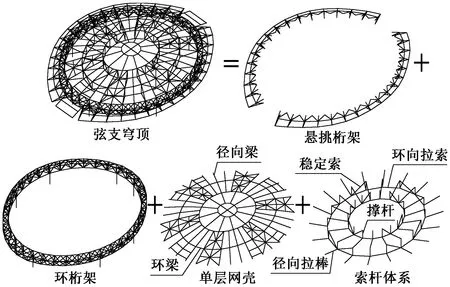
图6 弦支穹顶结构组成

(1)环桁架及竖向支承

按建筑外形要求于8根钢柱上布置投影面为椭圆形的环桁架;由两片平面桁架通过水平联系杆件组成空间立体桁架,立体桁架高度由2.7m至3.8m不等;钢柱与环桁架、钢柱与下方的大跨度桁架均为刚接。

(2)悬挑桁架

在环桁架外侧布置34榀立面桁架,每榀立面桁架之间设置斜杆及水平联系杆件,内侧与环桁架结构相连,外侧向外悬挑,长轴方向与主体结构屋面连接。

(3)单层网壳

在环桁架内侧布置36根径向梁,沿环向布置3圈环向梁,形成肋环型单层网壳。为了满足建筑造型及结构布置的需求,根据屋盖曲面的走向特点,通过若干关键控制点及环向分割数,在屋盖异形曲面上进行投影,得到各圈网壳节点位置,杆件长度分布均匀,整体性能较好。其网壳同一圈节点不在同一标高,呈从长轴端点向短轴端点逐渐增大高度的趋势,因此同圈撑杆上节点标高不一致,如图7所示。此外,还在荷载集中位置布置斜杆及加密的环向杆以提高局部网壳的刚度。

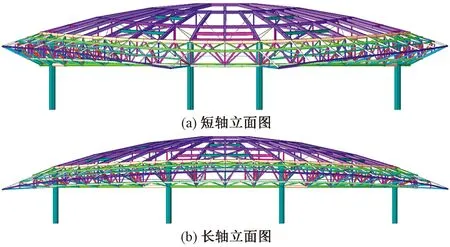
图7 弦支穹顶立面图

(4)索杆体系

下部布置2圈Giger型索杆体系,荷载集中位置增加竖向稳定索以提高索杆体系的稳定性。撑杆上节点与网壳节点相连,同一圈节点不在同一标高,呈从长轴端点向短轴端点逐渐增加高度的趋势,而同一圈撑杆下节点为同一标高。因此环向拉索均为水平布置,分两圈布置。径向斜拉索对应环向拉索分两圈布置,内圈每根径向斜拉索与水平面夹角为14°～25°,外圈每根径向斜拉索与水平面夹角为16°～22°。内圈撑杆长度为3.88～4.26m,外圈撑杆长度为3.57～4.6m。

(5)构件材质

主要钢构件等级为Q355B;环向拉索采用强度等级为1 670MPa的密封索,内外圈环向索截面分别为φ50和φ85;径向钢拉杆采用强度等级为650级的等强钢拉杆,内外圈径向钢拉杆截面分别为φ40和φ70;稳定索采用强度等级为1 670MPa的钢丝束,截面为φ22。

2.3 荷载情况

结构自重由MIDAS Gen程序自动加载计算,并考虑1.1的节点增大系数;附加恒荷载:屋面附加恒荷载取1.65kN/m2,屋檐附加恒荷载3kN/m,水箱恒荷载为220kN/个,撑杆下节点索夹恒荷载为10kN/个;屋面构件搭接荷载:通过从整体模型中提取各工况的节点力,取最不利值添加至屋盖独立模型中予以考虑;活荷载:屋面附加活荷载0.5kN/m2,半跨活荷载不均匀布置0.5kN/m2;风荷载:基本风压取为0.9kN/m2,根据《建筑结构荷载规范》(GB 50009—2012 )[16]的规定和风洞试验报告分别进行分析,考虑0°、90°、180°、270°四种风向,取包络进行计算,以保证结构安全;地震作用:本项目结构设计使用年限为50年,抗震设防烈度7度,设计地震分组第1组,设计基本地震加速度为0.10g,场地类别为Ⅱ类场地,建筑抗震设防类别为重点设防类(乙类);温度作用:按升温30℃,降温30℃考虑。

3 支承条件的影响分析

3.1 整体模型与独立模型的对比

鉴于本工程弦支穹顶结构支承条件的异常复杂性,对其弹性不均匀支承条件的影响进行对比分析。分别建立整体模型与独立模型,其中独立模型(图7)中结构柱下方为固定支座。通过多工况下的计算分析,对于本工程结构,其控制工况为静力工况,因此进行1.0恒荷载+1.0预应力的基本静力工况下结构受力及变形的对比,以评估支承条件的影响。两个模型计算结果的受力与变形差值如图8所示,上部网壳竖向位移云图如图9所示。从图8、9可得:

图8 支承条件对结构受力与变形的影响

图9 上部网壳竖向位移云图/mm

(1)竖向位移方面

弹性不均匀支承条件对节点竖向位移的影响较大,尤其是对结构柱周围的结构区域,其影响表现为局部性;结合图3和图9可知,由于长、短轴方向结构柱的落点不同,长轴方向的桁架支承刚度远小于短轴方向,因此支承条件对长轴和短轴方向的节点竖向位移影响程度不一。长轴方向的竖向位移变化较大,且呈现从外圈到内圈逐渐减小的趋势;而短轴方向竖向位移变化较小,由于其内圈远离支座,受长轴方向内圈位移的影响,因此呈从内圈到外圈逐渐减小的趋势。

(2)拉索索力方面

个别拉索的索力偏差超过90%,长轴方向内圈的部分环向索和径向索索力变化较大,这是内圈斜索上、下节点的竖向位移差的变化造成的。在不均匀弹性支承条件影响下外圈撑杆上节点与环桁架一同向下变形,其外圈斜索上、下节点的竖向位移差变化较小,因此外圈拉索内力变化相对较小。

(3)单元等效应力方面

由于支承刚度的不均匀分布,环桁架结构不均匀下挠,因此环桁架单元的应力变化较大,最大近50MPa,而其余大部分单元应力变化基本在20MPa以内。

因此,支承条件对结构受力的影响不可忽略,独立模型计算时需充分考虑其影响。

3.2 弹性不均匀支承条件的简化模拟

由于存在两根钢柱同时落在同一榀桁架的情况,若采用常规的弹性支座模拟则无法考虑钢柱群对下部桁架受力及变形的耦合影响。因此本文采用强制位移的形式来模拟弹性不均匀支承条件,即从整体结构计算模型中提取柱脚的竖向位移,以柱脚强制位移的形式施加在屋盖独立模型中,从而考虑下部支承条件对屋盖结构的影响,形成其屋盖结构的简化计算模型。

1.0恒荷载工况下整体模型各柱脚的竖向位移及简化模型柱脚竖向强制位移见表1,以整体模型中竖向位移最小的柱脚1(图3中结构柱1的柱脚,余同理)为基准,将其他柱脚与柱脚1的竖向位移差值作为简化模型中的柱脚强制位移。

表1 1.0恒荷载工况下整体模型各柱脚的竖向位移及简化模型柱脚竖向强制位移/mm

简化模型中,1.0恒荷载工况下各柱脚的竖向强制位移分布如图10所示。

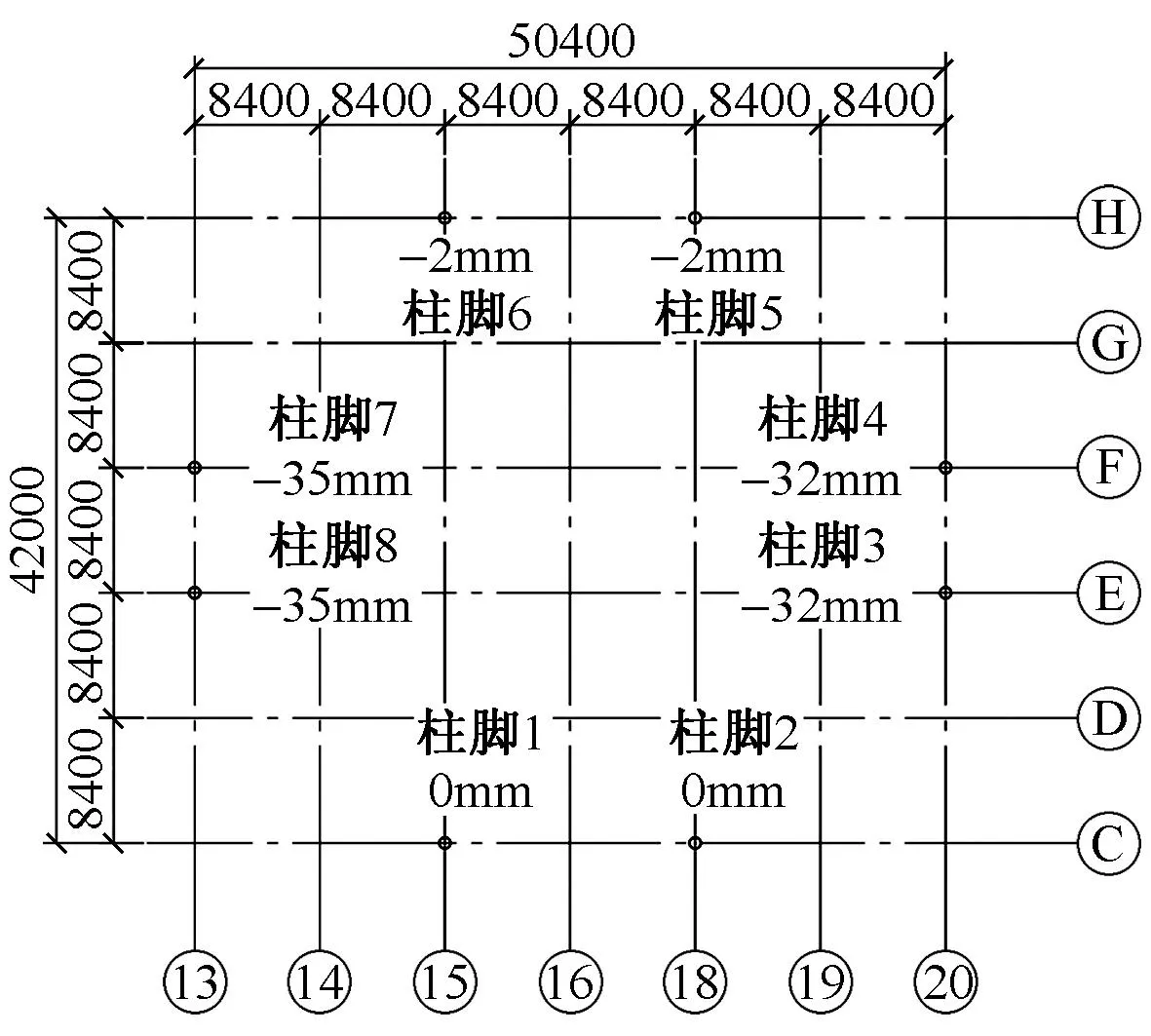
图10 简化模型中钢柱柱脚竖向强制位移分布

为了验证简化模型的合理性,对1.0恒荷载+1.0预应力的工况下整体模型及简化模型的计算结果进行对比,对比结果如表2所示。

表2 整体模型与简化模型的计算结果对比

由于将其他柱脚与柱脚1的竖向位移差值作为简化模型的柱脚竖向强制位移,因此简化模型与整体模型的理论竖向位移差值为28mm。从表2可知,整体模型的最大竖向位移为-86.0mm,简化模型的最大竖向位移为-57.6mm,两者差值与理论差值吻合。此外,整体模型与简化模型的水平位移、梁单元应力、索力、撑杆轴力等均基本一致,因此可采用简化模型替代整体模型,以提高计算效率、减少下部结构的干扰,并用于后续屋盖结构的详细分析以及预应力优化分析中。

4 结构静力分析

4.1 找力分析

以1.0恒荷载+1.0预应力的荷载组合下撑杆上节点竖向位移和索杆体系水平位移最小为控制目标,进行找力迭代分析。找力分析计算结果如图11所示。如图11所示,1.0恒荷载+1.0预应力的荷载组合下,整体结构最大竖向位移为-57.64mm(包含下部支承结构的强制位移);索杆体系最大水平位移为11.50mm,出现在内圈环向索长轴方向端点;拉索最大索力为1237.95kN,撑杆最大轴力为305.45kN。

图11 找力分析计算结果

4.2 变形验算

1.0恒荷载+1.0活荷载+1.0预应力(基本荷载组合)下,整体结构竖向变形如图12所示,最大竖向位移为-73.65mm,位于长轴方向悬挑桁架端部,除去下部支承结构强制位移的影响,该位置相对竖向位移为-33mm,而屋盖中部最大竖向位移为-37mm,因此屋盖最大挠度为37mm/42000mm=1/1 135,满足不大于规范限值1/400的要求[17]。

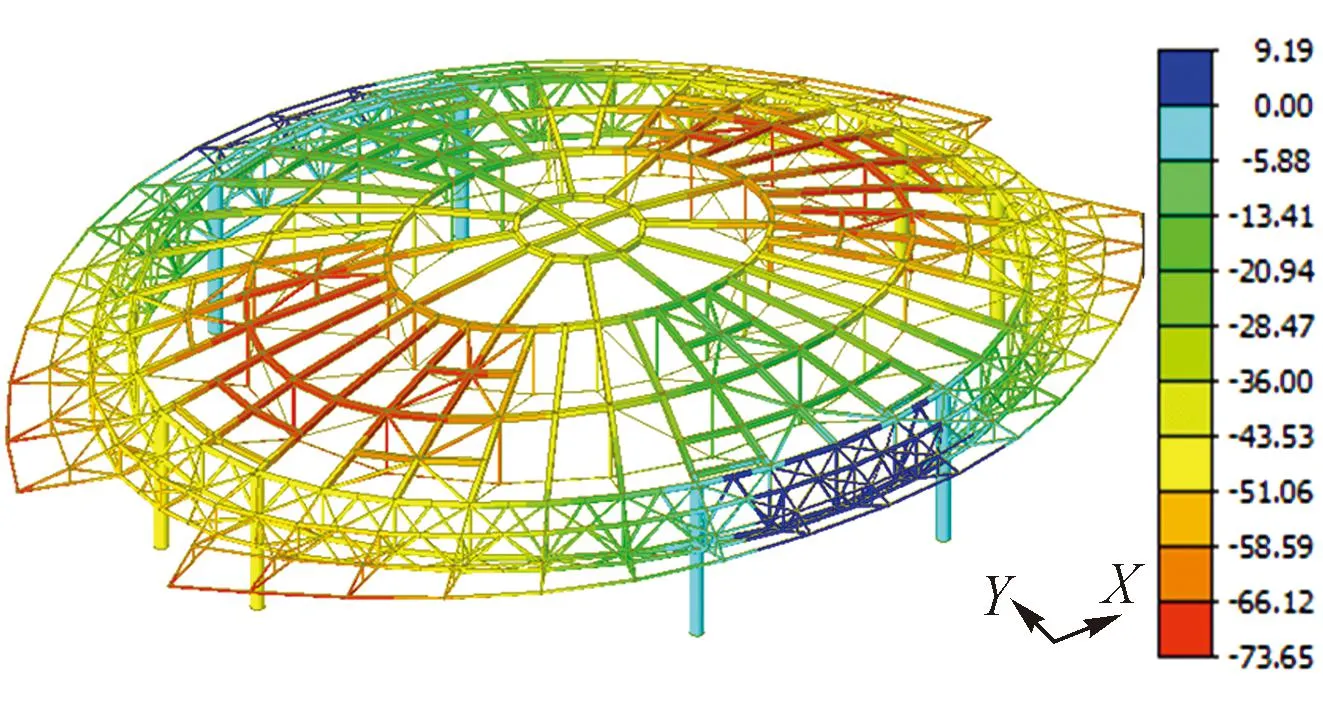
图12 基本荷载组合下整体结构竖向变形/mm

4.3 构件验算

根据《建筑结构荷载规范》(GB 50009—2012)[16],考虑恒荷载、预应力、活荷载、风荷载、温度、单向水平地震、竖向地震等各种工况的组合,非地震组合和地震组合下结构构件的包络应力比如图13所示。由图13可知,非地震组合下结构最大应力比为0.81,地震组合下结构最大应力比为0.53,满足《钢结构设计标准》(GB 50017—2017)[17]要求,且各工况下拉索均不出现松弛。

4.4 整体稳定性分析

采用ANSYS软件对钢屋盖进行整体稳定性分析。分析模型采用屋盖钢结构独立模型,拉索、钢拉杆及撑杆采用LINK10单元模拟,其余杆件均采用BEAM188单元进行模拟。柱脚均为固定约束。对钢屋盖施加点荷载及线荷载,施加的荷载组合为A×(恒荷载+活荷载)+预应力,A为荷载因子。整体稳定性分析结果如图14所示。由图可见,10倍荷载下的特征值为1.00437,因此其特征值屈曲因子为10,考虑材料非线性和1/300跨度的最低阶屈曲模态缺陷后,其双非线性屈曲因子为6.0,满足《空间网格结构技术规程》(JGJ 7—2010)[18]的要求。

5 布索形式对比研究

以本项目为例,采用基于刚性索法和改进模拟植物生长算法(简称PGSA算法)的预应力优化方法,对不同布索形式下弦支穹顶结构进行静力及稳定性能的对比分析。

5.1 四种布索形式

结合工程实践案例及文献[9-15],提出四种布索形式(图15):撑杆等长度、斜索等角度、马鞍形、撑杆杆底等标高,撑杆等长度布索方式为同一圈撑杆的长度相同;斜索等角度布索方式为同一圈斜索与水平面夹角相同;马鞍形布索方式为同一圈撑杆的杆底标高,从长轴端点向短轴端点逐渐减小,长轴端点杆底标高最大,短轴端点杆底标高最小;撑杆杆底等标高布索方式为同一圈撑杆杆底标高相同。四种布索形式的结构布置参数对比如表3所示。

表3 四种布索形式的结构布置参数对比

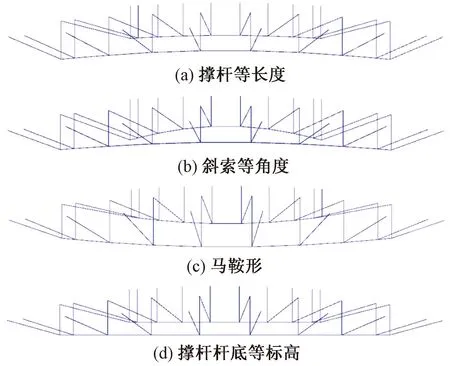
图15 四种布索形式——以长轴方向立面为例

5.2 基于刚性索法和改进PGSA算法的预应力优化

对于预应力空间结构,其预应力分布与其结构布置密切相关。为了更好地对比不同布索形式下的结构性能,需对不同布索形式下的结构分别进行预应力优化。

针对弦支穹顶结构的预应力优化问题,引入改进PGSA算法,在文献[19]的基础上,进一步结合刚性索法,提出基于刚性索法[8]和改进PGSA算法的弦支穹顶预应力优化方法。首先通过刚性索法得到弦支穹顶结构的初始预应力分布,然后以该预应力分布为初始生长点中施加的拉索预应力,采用改进PGSA算法进行预应力优化,优化流程如图16所示。该方法充分结合弦支穹顶的结构特点与智能优化算法的优势,避免了初始生长点选择不当对优化效率的不利影响,大大提高了优化效率。

图16 基于刚性索法和改进PGSA算法的预应力优化流程

5.3 静力及稳定性能对比

根据四种布索形式,分别建立结构模型。对于常规的弦支穹顶结构,其预应力的优化目标可取为撑杆上节点的位移最小,即下部的拉索预应力可完全抵消外荷载作用下的竖向变形,从而保证基本工况下弦支穹顶结构的位形与设计位形一致。但对于类椭圆形弦支穹顶结构,其同一圈撑杆上节点的竖向变形不尽相同,因此选取每一圈撑杆上节点竖向位移的平方和作为预应力的优化目标,以尽可能降低基本工况下弦支穹顶结构位形与设计位形的差值。

以1.0恒荷载+1.0活荷载+1.0预应力的工况下各圈撑杆上节点竖向位移的平方和最小为目标,以各圈的环向索及径向索的预应力为优化变量,根据对称性的原则,将内外两圈环向索及径向索进行分组,共10个环向索预应力变量和10个径向索预应力变量。采用基于刚性索法和改进PGSA算法的预应力优化方法,进行预应力优化,并对预应力优化后的弦支穹顶结构静力及稳定性能进行对比分析,对比结果如表4所示。由表4可得:

表4 四种布索形式的结构性能对比

(1)从撑杆上节点竖向位移平方和来看,撑杆杆底等标高布索形式明显比其余三种索形式更小,说明该布索形式下,整个上部网壳的竖向位移分布更为平均,变形更为协调,而斜索等角度及马鞍形的布索形式下竖向位移分布较为不均匀。

(2)从整体结构的稳定性能来看,四种布索形式下整体结构的特征值屈曲和双非线性屈曲因子均较为接近。

(3)对于撑杆等长度的布索形式,由于本工程屋盖为异形壳面,同一圈撑杆上节点的标高不同,造成径向斜索与水平面的夹角不同,即索杆体系对上部网壳的支承刚度各不相同,造成索力及变形分布较为不均匀,其整体结构水平变形明显较大。

(4)对于斜索等角度的布索形式,其索杆体系对上部网壳的支承刚度基本相同,由于本工程为类椭圆形弦支穹顶,上部网壳刚度分布不均匀,再加上荷载的极其不均匀分布,造成其受力及变形也较为不均匀。

(5)在常规的类椭圆形弦支穹顶中,马鞍形布索形式下结构具有较好的性能,能有效地调节长短轴网壳的刚度差值,使得结构的变形及内力分布更为均匀。但在本工程异形弦支穹顶结构中,由于存在异形的网壳曲面、不均匀分布的荷载、不连续支承的边界条件以及相对不大的结构跨度等特点,马鞍形布索形式并未发挥出其优势,其竖向位移峰值最大,且其竖向位移、撑杆轴力等分布相对较不均匀。

(6)对于撑杆等长度、斜索等角度以及马鞍形的布索形式,其环向索均为空间双曲线形分布,由于本工程跨度不大,空间双曲线形引起的环向索折角较为明显,环向索的双曲弯曲对环向索索体会产生一定的不利影响,此外环向索的倾斜对索夹的抗滑能力也提出了更高的要求。

(7)而撑杆杆底等标高的布索形式下,其位移峰值、位移分布、索力分布以及撑杆轴力分布等较为均匀,且其环向索为平面类椭圆形布置,有效避免了双向弯曲对索体的不利影响。

因此,基于上述整体结构的静力及稳定性能对比分析结果,选取撑杆杆底等标高的布索形式作为最终的布索形式。

6 结论

(1)采用的肋环型单层网壳+Giger型索系组成的弦支穹顶,通过采用稳定索、网壳面内支撑、撑杆杆底等标高等方式,经结构计算分析,能满足边界、荷载、外形等复杂条件下结构的性能要求。

(2)弹性支承条件不仅对弦支穹顶结构的变形有较大的局部影响,对其索力分布及单元应力也有不可忽略的影响,结构计算分析中需充分考虑弹性不均匀支承条件的影响。

(3)对于上部网壳刚度、撑杆上节点标高、支承条件、荷载等均为不规则分布的复杂情况,采用撑杆杆底等标高的布索形式,其受力及变形分布更为均匀,静力及稳定性能相对较好,且有效避免了双向弯曲对环向索索体的不利影响,为最终采用的布索形式。