地铁邻近超高层建筑振动响应及减振降噪研究

李伟科, 林治平, 黄俊光, 毕俊伟,2, 李长江, 邱艳萍

(1 广州市设计院集团有限公司，广州 510620；2 华南理工大学土木与交通学院，广州 510641)

0 引言

近年来,随着地铁等城市轨道交通迅速发展和城镇化的不断推进,城市用地趋于紧张,新建建筑与既有地铁隧道的距离越来越近。与此同时,地铁运营导致的邻近建筑结构振动和二次辐射噪声问题日益突出并受到广泛关注,地铁荷载下近邻建筑的减振降噪问题也逐渐成为研究热点[1]。

地铁邻近建筑的减振降噪措施可分为振源、传播路径和邻近建筑3个方面[2]。对于邻近既有地铁的拟建建筑,从振源角度采取减振降噪措施会对地铁运营产生较大影响,因此主要从其他两方面进行考虑。宋晶等[3]对比分析了地下连续墙外贴防振橡胶和在地下连续墙与地下室结构墙之间设置防振橡胶的减振降噪效果。胡皓宇[4]采用有限元模拟和现场试验对比分析了不同肥槽减振方案,研究表明采用弱剪减振材料+混凝土的肥槽回填方案能有效降低室内振动。Pan等[5]提出了一种用于基坑肥槽回填的复合减振层,并指出该肥槽回填材料可为建筑基础提供充分约束,同时又能起到较好的减振效果。此外,张涛等[6]利用SAP2000程序分析了砂垫层对地铁环境振动的减振效果,研究表明在地下室底板下虚铺砂垫层可有效减小地铁运行引起的建筑振动。吴燕等[7]利用现场试验分析了在建筑基础底部设置砂袋垫层的减振效果,结果表明砂袋垫层能显著减小轨道交通导致的建筑物室内水平和竖向振动。上述研究仅针对单一减振降噪措施,既有研究指出采用多种措施组合的方式能更有效地降低交通荷载导致的环境振动[8]。然而,现阶段有关地铁近邻拟建超高层建筑组合减振降噪措施的研究少有报道。

基于此,本文以广州地铁3号线某邻近拟建超高层建筑为背景,利用MIDAS GTS NX建立隧道-土体-建筑物的3维有限元数值模型,分析地铁荷载下建筑物各楼层的振动和二次辐射噪声特性。在此基础上,结合建筑基坑围护结构,创新性地提出地下连续墙加深且嵌固段外贴橡胶层、肥槽回填减振耗能材料、基底设置PVC减振垫层的组合措施,并对其减振降噪效果进行研究。

1 模型建立与验证

1.1 工程概况

该拟建项目为超高层商办综合体,高172.5 m,地上40层,地下设4层地下室,室外地坪标高8.5m,地下室地板标高-11.1m,位于广州市天河区黄埔大道南侧、华夏路西侧地段,东侧近邻地铁3号线,与地铁的相对位置关系如图1和图2所示。图2中数字为土层厚度,地铁隧道与建筑地下室基坑的最小水平净距约为9m。直径6.4m的圆形地铁隧道处于中风化及微风化的泥质粉砂岩中,其结构形式为装配式钢筋混凝土单层衬砌,采用盾构法施工,管片厚0.3m,混凝土强度等级为C50。轨面标高为-12.16 ～-12.60 m。建筑基坑开挖深度约为21m,围护结构采用800mm厚地下连续墙+3道钢筋混凝土支撑,其中地下连续墙嵌固深度为3m。连续墙接口处采用φ600@400双管旋喷桩,旋喷桩穿过砂层进入相对不透水层不少于2m。地连墙与地下室侧壁合建,即采用两墙合一形式。

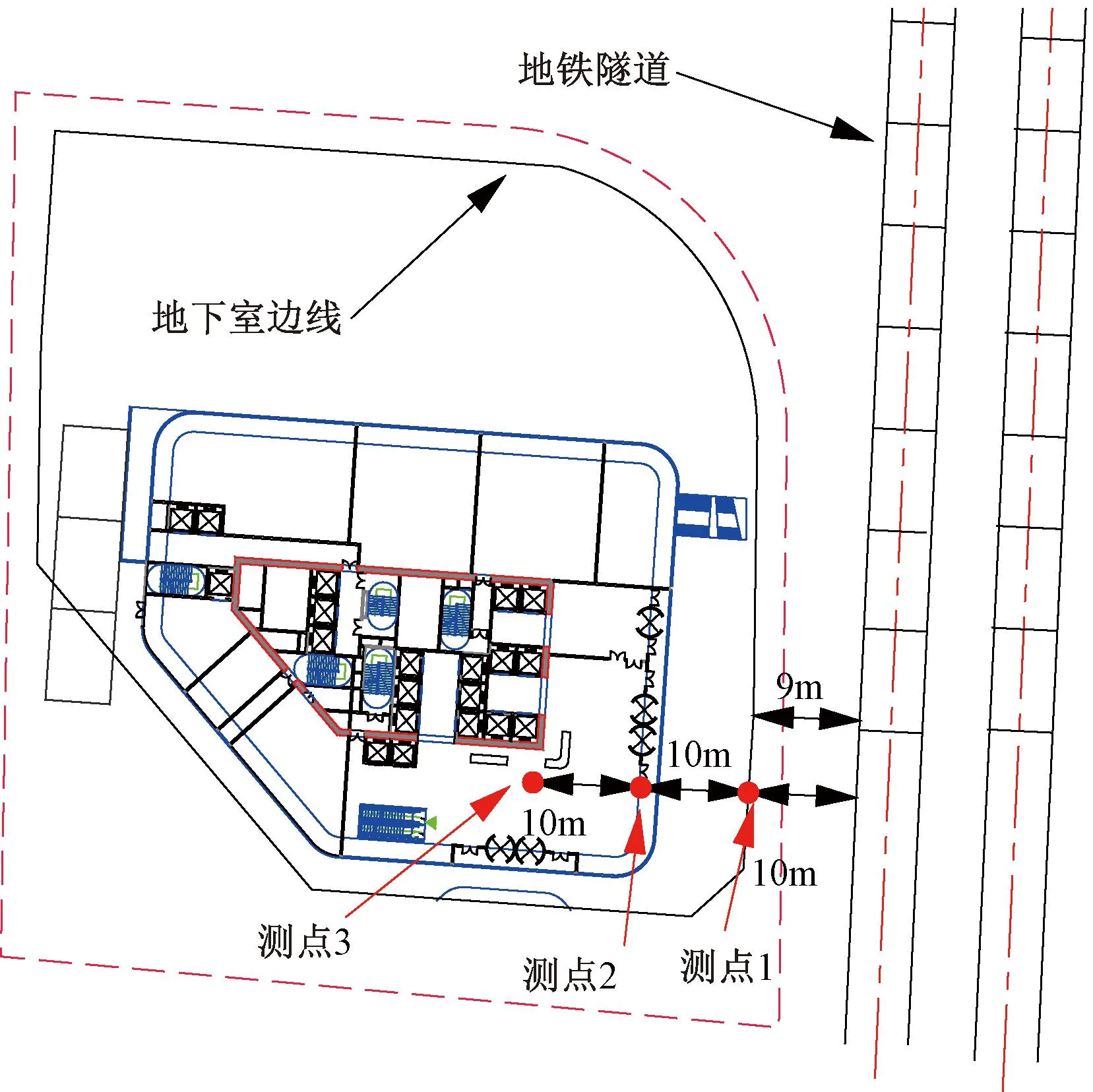
图1 建筑与地铁平面位置关系

1.2 三维数值模型的建立

本文采用MIDAS GTS NX有限元软件建立了隧道-土体-建筑物的三维数值模型,如图3所示。采用1A315EB型三方向振动加速度传感器,分别实测昼间和夜间广州地铁3号线列车运行引起的隧道壁振动。如图4所示,实测并记录距轨道1.25 m高处的隧道壁振动,并采用隧道壁振动加速度时程作为模型的输入荷载[9-10],其中昼间单次列车通过引起的竖向振动加速度时程曲线如图5所示。

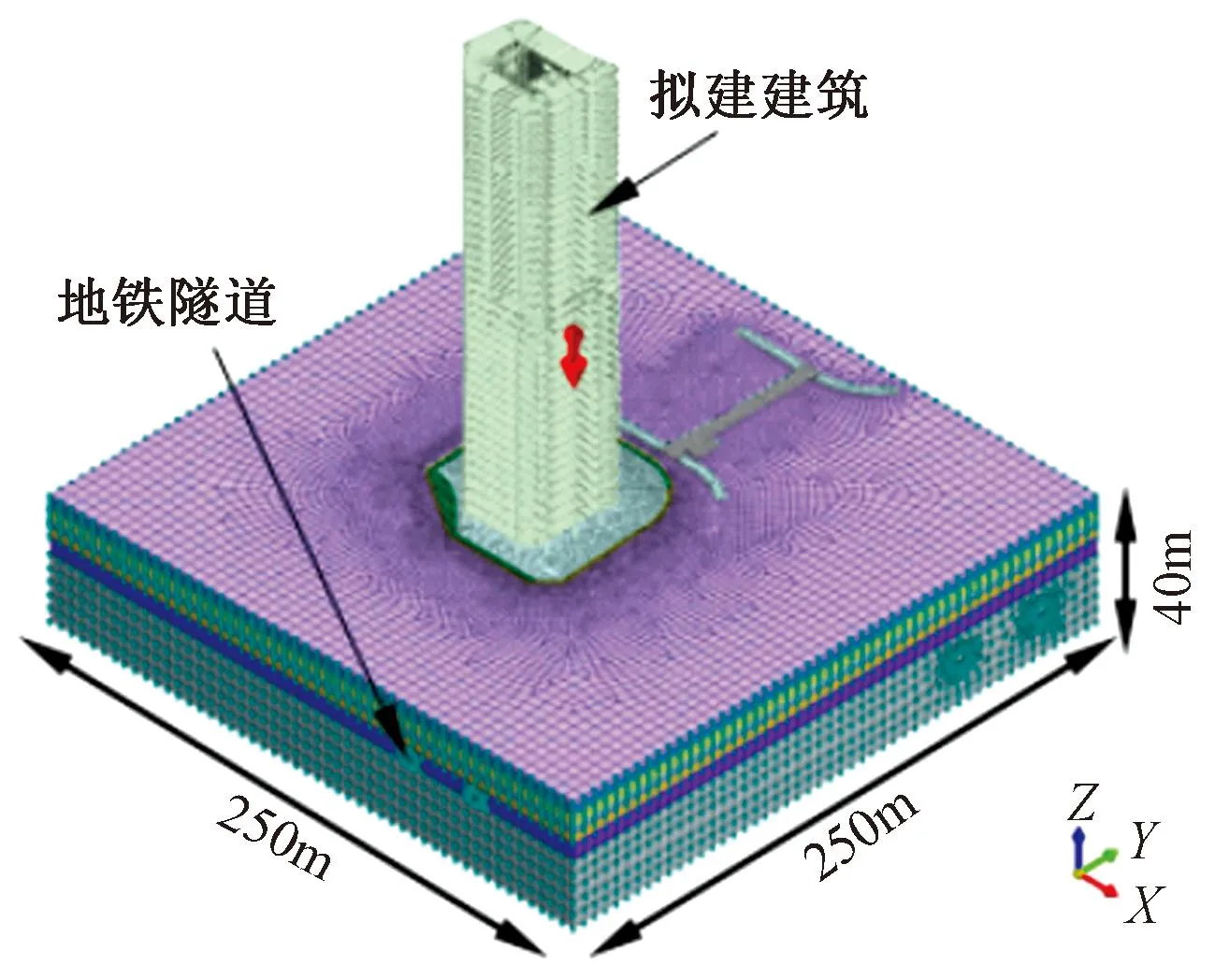
图3 三维数值模型

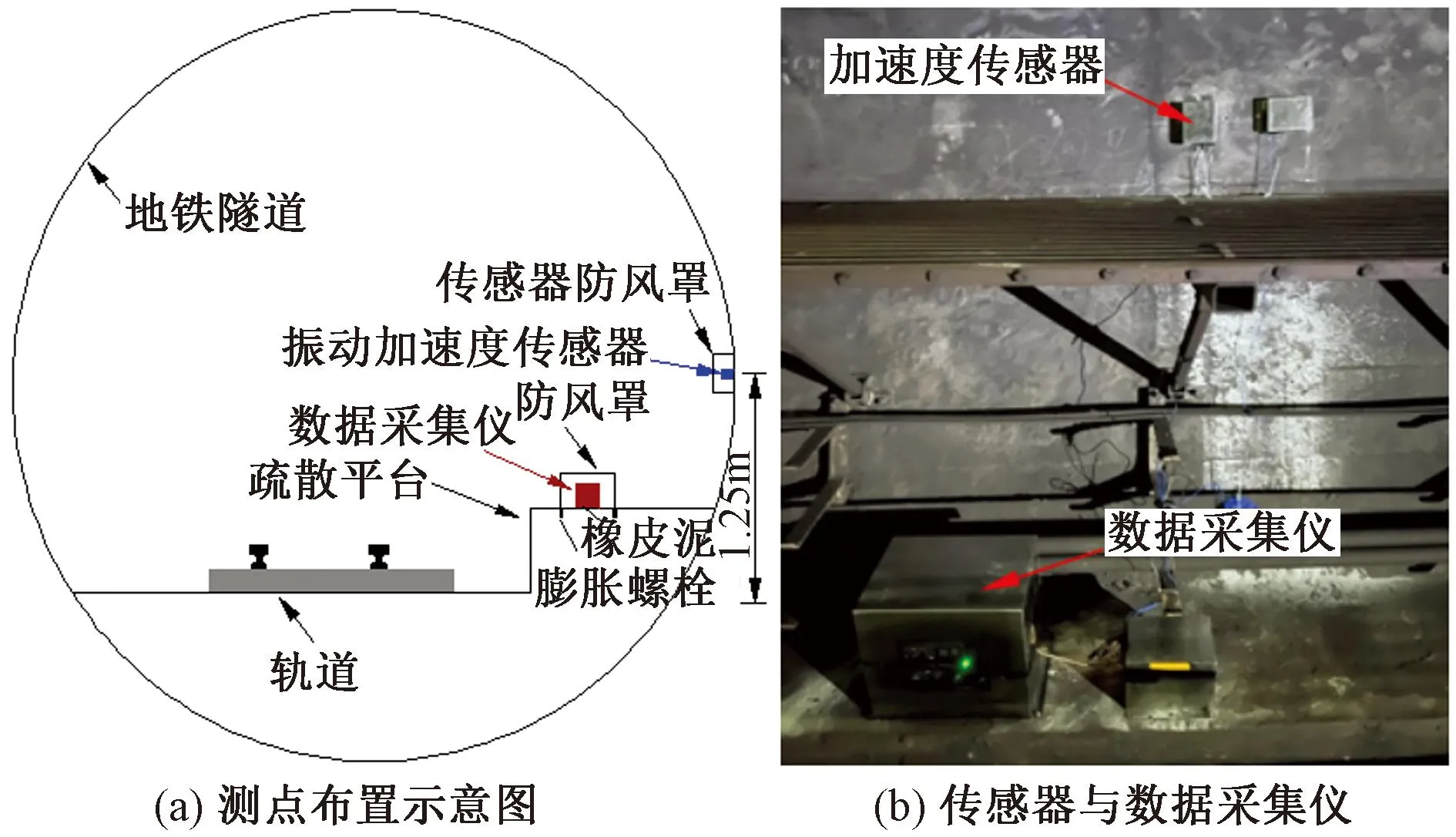
图4 隧道内测试图

图5 隧道内壁竖向振动加速度时程曲线

基于既有研究成果[11-12],当模型边界与隧道间距为隧道直径的2～6倍时,可有效减少模型尺寸效应对计算结果的影响。综合考虑建筑物与隧道的位置关系,建立的模型尺寸为250m(长)×250m(宽)×40m(高)。模型中土体及地下连续墙采用3维实体单元,地铁隧道、建筑结构板采用壳单元,建筑的梁、柱结构采用梁单元,模型各部分材料参数如表1所示。

表1 模型土层计算参数

模型底面采用固定边界,为避免模型截断边界的反射波对有限元动力计算结果造成影响,采用3维等效黏弹性边界[13-14],模型四周侧向边界上设置切向和法向的弹簧-阻尼单元。考虑地铁和在的优势频段(1.0～80.0Hz)[13],分别选取5.0Hz和80.0Hz作为Rayleigh阻尼系数α、β的计算频率,算得α=1.773,β=1.120×10-4。地铁环境振动研究中通常仅考虑单次列车的荷载作用,不同于列车循环荷载,单次列车荷载引起的土体固结沉降和结构与土的相对位移可忽略不计[15]。

1.3 模型验证

在隧道壁振动测试期间,分别对昼间和夜间地铁运行引起拟建场地距隧道不同水平距离处的地面振动进行实测,测点位置见图1,并与数值计算结果进行对比,从而验证本文三维有限元数值模型的正确性。

图6为昼间测点1的地面竖向振动实测与计算结果对比图。由图6(a)分析可知,地面振动计算加速度时程与实测结果趋势基本一致,时程曲线中可清晰地观察到列车经过时各轮对引起的一系列周期性峰值。如图6(b)所示,计算结果能较好地反映出地铁荷载下地面振动的频域特性,并能准确地判定地面振动的主频。对比分析发现,实测地面振动的高频成分更为丰富,这主要是由于现场测试情况复杂且影响因素众多所致。

图6 测点1实测与计算地面竖向振动结果对比图

为进一步验证模型的正确性,图7为距隧道不同距离处地面竖向振动加速度振级的计算与实测结果。由图可知,数值模型计算结果与实测结果吻合较好,表明本文所建立的三维有限元模型能较好地反应地铁运行引起的振动和传播衰减规律。

图7 实测与计算地面竖向振动加速度振级变化曲线

2 建筑振动及二次辐射噪声

分别选取昼间和夜间各5列次地铁荷载下实测的隧道壁振动加速度时程作为输入荷载,计算并分析地铁运行引起的建筑物各层振动和二次辐射噪声特性。

图8为昼间单次地铁列车运行引起的建筑各楼层振动云图。由图8和图3分析可知,地铁荷载下拟建超高层建筑各楼层近轨道一侧振动均明显大于距轨道较远一侧,且建筑各楼层转角处振动显著大于其他位置。为考虑地铁环境振动对拟建建筑影响的最不利情况,以图8中各楼层近地铁一侧转角处作为采样点,研究地铁运行对拟建超高层建筑各楼层振动及二次辐射噪声的影响。

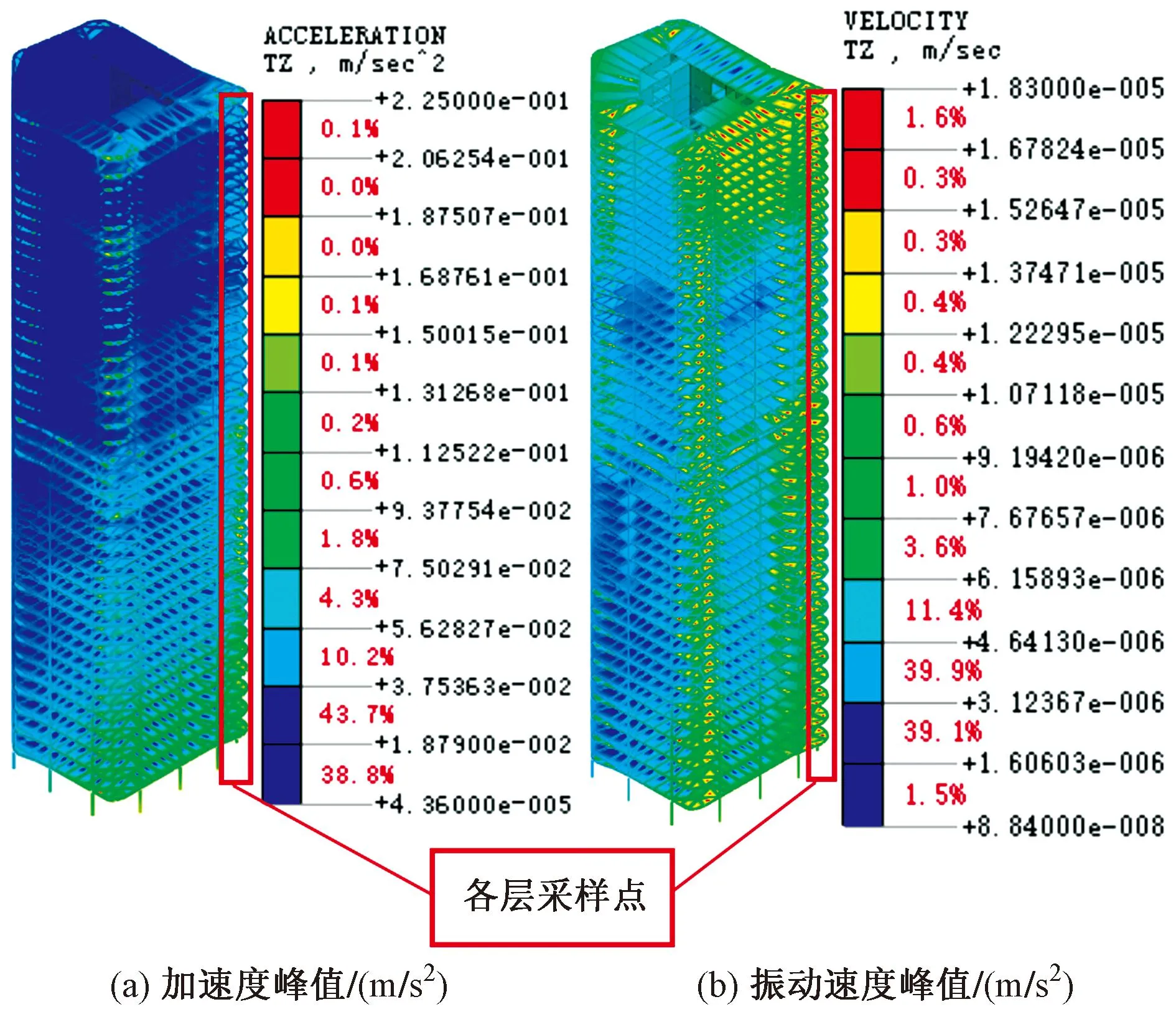
图8 地铁运行引起建筑各楼层振动云图

2.1 最大分频加速度振级

图9为昼间和夜间地铁荷载下拟建超高层建筑各楼层的最大分频加速度振级。由图9(a)可知,地铁运行引起的建筑各楼层最大分频加速度振级呈现“两端大、中间小”的趋势。首层振动最大,随楼层升高逐渐减小,并在中间楼层(17～21层)达到最小值。此后,最大分频加速度振级随楼层进一步升高持续增大,表现出类“鞭梢效应”[16]。此外,地铁荷载下拟建超高层建筑9～35层最大分频加速度振级满足《城市轨道交通引起建筑物振动与二次辐射噪声限值及其测量方法标准》(JGJ/T 170—2009)[17](简称测量标准)中关于居住、商业混合区的昼间振动限值70dB,而其他楼层均不满足该限值要求。由图9(b)可知,夜间地铁运行引起的建筑各楼层振动分布规律与昼间相似,各楼层最大分频加速度振级均略大于昼间,且夜间地铁荷载下建筑各楼层振动均难以满足测量标准的限值67dB。

图9 建筑各楼层最大分频加速度振级

2.2 二次辐射噪声

基于地铁荷载下建筑振动的计算结果和《环境影响评价技术导则 城市轨道交通》(HJ 453—2018)[18],地铁运行引起的建筑物室内二次辐射噪声最大1/3倍频程声压级Lp,i可由式(1)算得,其中式(1a)适用于层高2.8m、混响时间0.8s的一般装修房间,其他情况可由式(1b)算得。

Lp,i=LVmid,i-22

(1a)

Lp,i=LVmid,i+10logσ-10lgH-20+10lgT60

(1b)

式中:LVmid,i为单次列车通过时建筑物室内楼板垂向1/3倍频程振动速度级,dB,其中i为第i个1/3倍频程(i=1,2,3,…);σ为声辐射效率;H为房间平均高度,m;T60为室内混响时间,s。

单次列车通过时建筑物室内空间最大等效连续A声级可由式(2)算得。

(2)

式中:LAeq,Tp为单次列车通过时建筑物室内空间最大等效连续A声级,dB(A);Cf,i为第i个频带的A计权修正值,dB;n为1/3倍频程带数。

地铁运行引起的拟建超高层建筑各楼层二次辐射噪声级分布如图10所示。由图10可知,与最大分频加速度振级类似,昼间和夜间建筑首层的噪声级最大,且均随楼层的升高先减小后增大,其中19层的噪声级最小。同时,不同于最大分频振级,昼间和夜间各楼层的二次辐射噪声级均大于测量标准的相关限值(昼间41dB(A),夜间38 dB(A))。

图10 建筑各楼层二次辐射噪声

3 建筑减振降噪分析

3.1 减振降噪方案

地铁荷载下拟建超高层建筑昼间和夜间的振动及二次辐射噪声无法满足相关规范限值要求,需采取适当的减振降噪措施。考虑工程投资成本,结合建筑基坑围护结构,本文拟采用如图11所示的组合减振降噪方案。由图11可知,再原有基础上进一步增加地下连续墙的埋深,并超过地铁隧道埋深不小于3m,在地下连续墙嵌固段以及嵌固段以上1m范围内的外侧设置50mm厚橡胶减振层。同时,采用减振耗能材料对基坑肥槽进行回填,其中地下2层地下室以下深度范围回填厚度为0.5m的泡沫混凝土,地下2层地下室以上回填0.5m厚的中粗砂。

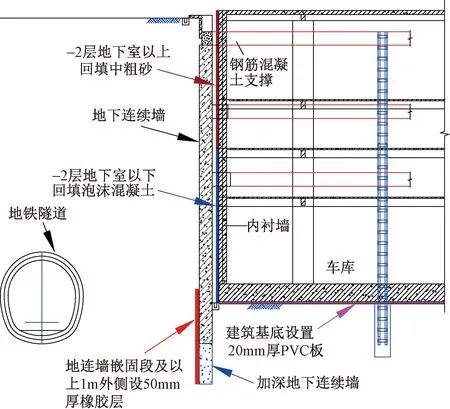
图11 减振降噪方案

此外,建筑基底设置20mm厚的PVC板作为减振垫层。综合减振方案的数值模型细部图如图12所示,其数值模型计算参数如表2所示。既有研究表明,交通荷载引起的环境振动属于小应变问题,土体与结构的相对位移等可忽略不计[19]。因此,有限元模型中结构物、各种减振降噪措施和土体之间采用共节点的方式连接[20]。

表2 减振降噪措施模型计算参数

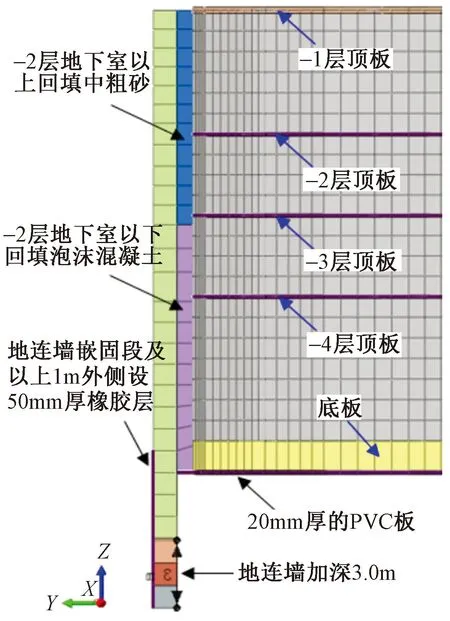
图12 减振方案数值模型细部图

3.2 减振降噪特性分析

考虑采取减振降噪措施前后,图13(a)为昼间单次列车运行引起的建筑首层竖向振动加速度时程曲线。由图13分析发现,从建筑首层竖向振动时程曲线中能清晰地观察到地铁列车轮对、转向架引起的周期性峰值。这表明采用组合减振措施能显著减小地铁运行引起的建筑首层振动加速度幅值。通过傅里叶变换对振动加速度时程曲线进行处理,得到如图13(b)所示的频谱图。由图13(b)可知,采用本文提出的组合减振措施能显著减小50Hz以上的振动。同时,采用组合减振措施会略微放大20～40Hz的振动,这主要是由于减振措施的阻尼和滤波作用,使地铁运行引起的振动主频向低频方向移动。

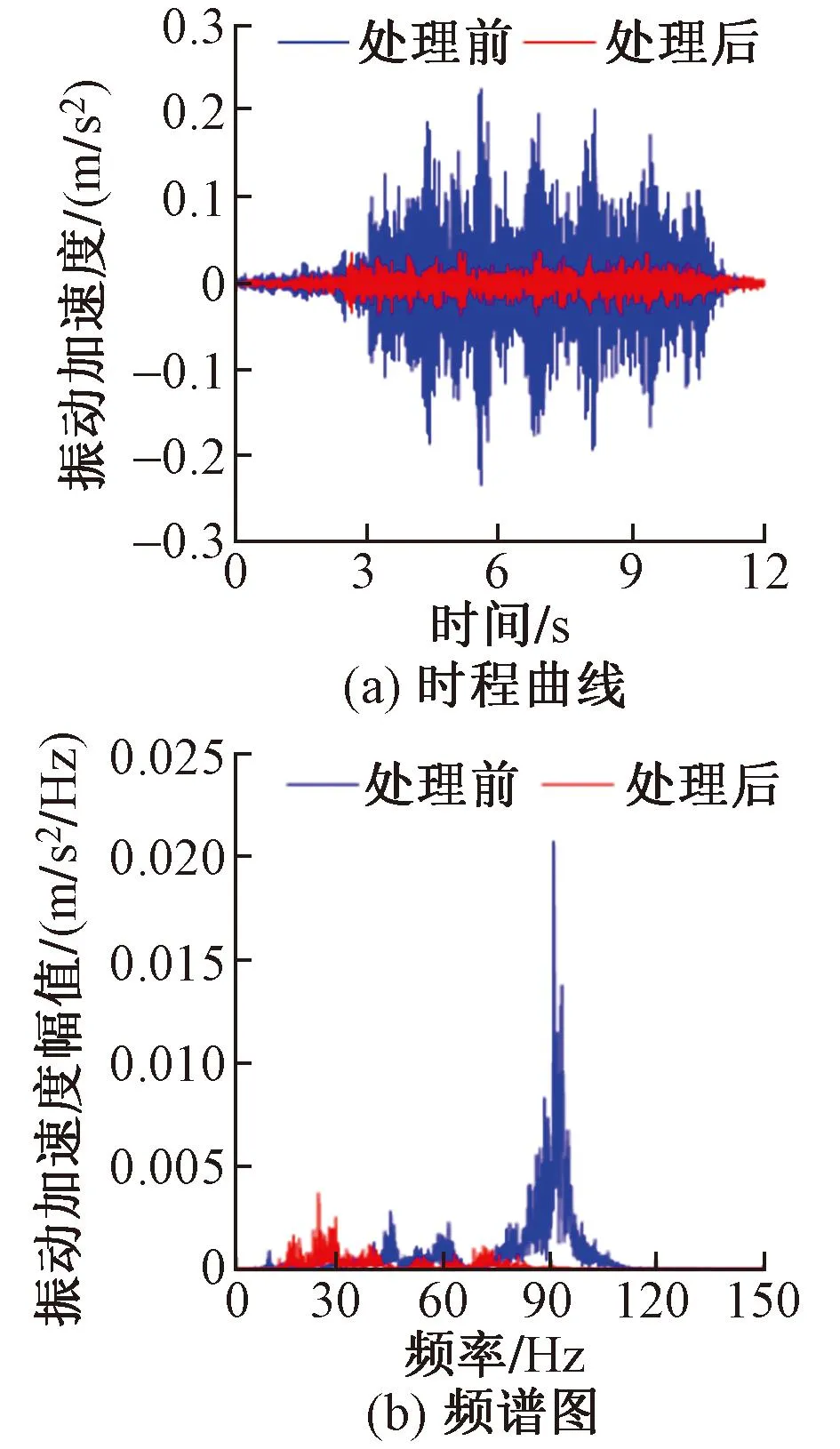
图13 建筑首层竖向振动加速度曲线

图14为采取减振降噪措施前后建筑首层的分频加速度振级曲线。由图14分析可知,采用组合减振措施能显著减小地铁运行引起的建筑振动,首层最大分频加速度振级由74.97dB下降至59.93dB,且对中、高频成分振动的减振效果尤为显著。值得注意的是,减振措施难以有效减小20～40Hz范围内的振动。因此,拟建超高层建筑结构以及其中各种动力设备的自振频率应避开此频段,避免引发共振现象。

3.2.1 建筑各楼层最大分频加速度振级

考虑组合减振降噪措施,图15为昼间和夜间地铁荷载下拟建超高层建筑各楼层的最大分频加速度振级。由图15可知,地铁运行引起的最大分频加速度振级随楼层的变化规律与图9相似。对比分析图9、15可知,采用组合措施能有效降低各楼层的最大分频加速度振级,对较低和较高楼层的减振效果优于中间楼层。同时,组合减振措施可使拟建超高层建筑各楼层昼间和夜间的振动均满足测量标准的相关限值要求。

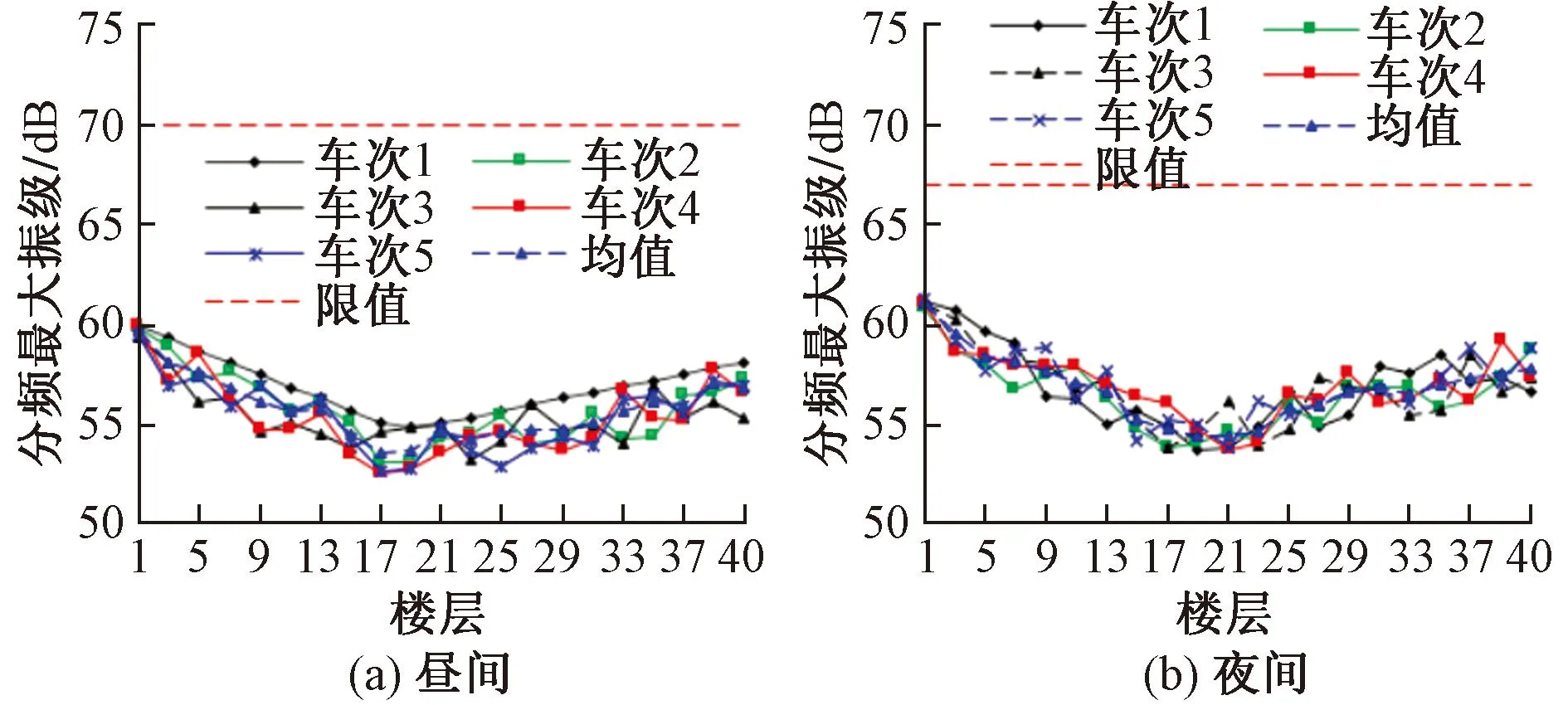
图15 建筑各楼层最大分频加速度振级

3.2.2 建筑各楼层二次辐射噪声

图16为采用组合减振降噪措施后地铁运行引发邻近拟建超高层建筑各楼层昼间和夜间的二次辐射噪声级。对比分析图16和图10可知,设置组合措施前后,噪声级随楼层均呈现“两端大、中间小”的分布规律。组合降噪措施可显著减小地铁运行引发拟建超高层建筑的二次辐射噪声级,并使各楼层噪声级均满足测量标准的相关限值要求。

图16 建筑各楼层二次辐射噪声

4 结语

(1)建筑首层的最大分频加速度振级和二次辐射噪声级最大,且振动和二次辐射噪声均随楼层增高呈现先减小后增大的趋势。

(2)采用地下连续墙加深且嵌固段外贴橡胶层、肥槽回填减振耗能材料、基底铺设PVC垫层的组合措施可有效减小地铁荷载下建筑振动,对50Hz以上频段振动的减振效果更为显著。

(3)组合减振降噪措施可使地铁邻近拟建超高层建筑各楼层的最大分频加速度振级和二次辐射噪声级满足相关规范限值要求。