基于光滑粒子元的水-沙两相流冲刷数值仿真

张嵘钊 ，熊文 †，刘川渟

（1.东南大学 交通学院，江苏 南京 211189；2.同济大学 土木工程学院，上海 200092）

水流侵蚀导致河床冲刷是水中建筑结构物常见现象，频繁发生于桥梁基础、防波堤、海底管线与堤坝下游等.2018 年，四川省堰塞湖泄洪导致下游河床剧烈冲刷，造成下游竹巴龙金沙江大桥冲毁，多座大桥下部基础被掏空而发生倾斜［1］；余文畴等［2］研究发现，大通站长江干流1950—2002 年年平均径流量中，每立方米水体平均含沙量达到47.2%，可见河床侵蚀作用十分显著.因此，有必要针对河床冲刷演进过程进行研究，以指导水工建筑物抗水设计，妥善预防及处置冲刷灾害，减少损失.

床底泥沙受到水流冲击，会在表面产生切应力，当泥沙表面屈服时，细颗粒泥沙将以推移质和悬移质的形式向下游推移、输送，并逐渐形成冲刷坑.冲刷诱因多种多样：暴雨、泄洪、溃坝等短时间内产生巨大峰值流量皆会造成河床剧烈冲刷.冲刷本质皆为河床自由表面发生高度非线性变形、破碎以及水和泥沙相互夹带.传统数值模拟方法基于欧拉坐标系建立流域模型，通过数值求解输沙方程和河床变形方程，获得床面各处高程变化，最后采用动网格技术以及体积分数法（VOF）实现河床形态可视化［3］.然而，动网格技术对于网格质量具有较高要求，冲刷伴随的河床大变形通常会造成网格畸变、计算不收敛等情况［4-5］；VOF 法通过捕捉水-沙交界面网格中材料体积分数分布情况实现河床形态可视化，因此精度受到交界面网格划分密度限制，对河床剧烈变形的区域，往往不能精准捕捉［6］.可见，传统网格法冲刷数值模型仍存在技术缺陷.

基于拉格朗日坐标系的光滑粒子流体动力学（Smoothed Particle Hydrodynamics，SPH）法，克服了传统网格法的固有局限，与欧拉法相比，SPH 法粒子本身具有质量，无需额外计算就能保证质量守恒；模拟复杂自由表面流时，无需追踪流体边界及不同流体交界面，对于复杂液面具有优秀的求解能力，可适用于模拟泥沙冲刷、输运等问题［7-11］.现阶段，SPH 法模拟河床冲刷主要有两种思路：其一，不进行土体粒子建模，使满足条件的边界粒子转化为土粒子进入流域参与计算.转化后土粒子视为离散元（DEM），不赋予材料本构，其运动方程受牛顿第二定律控制；土体与水体间考虑流固耦合作用力，土体粒子间考虑接触、碰撞作用［8，11］.然而，此类模型计算相对复杂，与真实冲刷关联较弱.其二，基于SPH多相流理论进行水体与土体建模［9-10］.土体粒子作为流体相可赋予材料本构，其变形与输运具有真实物理意义.

目前，基于SPH 多相流理论的泥沙冲刷研究多集中于河床溃坝冲刷，土体多为非黏性泥沙颗粒（以下简称为泥沙），泥沙粒子流变特性通常采用非牛顿流体进行模拟［8-14］.Manenti等［12］在冲淤研究中，基于非牛顿流体理论构建了土体模型，并分别对Mohr-Coulomb 屈服理论和Shields 理论进行了比较分析，推荐后者作为泥沙模型的材料屈服强度；Fourtakas等［13］引入了广义Herschel-Bulkley-Papanastasiou（HBP）模型进行土体建模，结合DP 强度准则确定材料屈服强度，并应用于水-沙两相流冲刷模拟中，获得了良好效果.

然而，现阶段基于SPH 多相流的冲刷数值仿真方法仍处于发展阶段：泥沙本构模型不统一，多数研究采用单一的土体强度准则，并集中于二维模型，对于三维泥沙冲刷模型及组合强度准则研究较少，对泥沙状态转变考虑不够详细［8-14］.由于SPH方法对于计算资源要求较高，三维模型需要耗费大量计算时间；同时冲刷过程中土体状态变化急促、剧烈，单一准则难以完整表征泥沙由静止到起动乃至输运的全过程特性变化，最终造成河床冲刷形态与实际仍有差距.

针对上述技术难题，本文提出了基于SPH 多相流模型的河床冲刷数值仿真改进算法，主要包含三个步骤：①构建泥沙粒子；②根据侵蚀模型和起动准则判断泥沙粒子状态并分类转化；③计算不同状态下泥沙粒子流变特性.具体来说，基于开源软件DualSPHysics 进行二次开发，编写出泥沙冲刷计算模块，利用开源CUDA 框架，进行GPU 计算加速；基于SPH 多相流理论与HBP 非牛顿流体模型，实现河床溃坝冲刷数值建模；引入Drucker-Prager 与Shields应力模型作为泥沙强度计算准则，考虑泥沙冲刷全过程中由沉积物到推移质再到悬移质的状态转变；最后，通过溃坝冲刷数值模拟，结合水槽试验验证模型准确性.

1 SPH基本理论

光滑粒子流体动力学（SPH）方法将连续流体离散为具有各种物理量的粒子，通过核函数实现粒子间相互作用，并按Navier-Stokes 方程进行运动控制.本节介绍了SPH 法控制方程及其离散形式，结合层流黏性应力与亚粒子（Sub-Particle Scale）紊流应力模型封闭N-S方程.

1.1 SPH法的积分插值理论

SPH 法根据相邻粒子物理性质在每个粒子周围进行局部积分，从而更新其物理量.相邻粒子由核函数检索，用W表示.

核函数W是关于光滑长度h的函数，其作用是将连续微分方程基于插值函数在特定点处进行积分，任意物理量连续形式用F可表示为

式中：F代表粒子的任意物理量；r和r'分别表示中心粒子和邻域粒子位置矢量；h为光滑长度.将F在A点插值并离散化，则其离散形式表达为

式中：下标a表示中心粒子；下标b表示邻域粒子；Δvb表示邻域粒子体积.核函数选取参照Fourtakas等［13］的研究采用五次核函数［15］：

式中：q为粒子间距与平滑长度的比值.

1.2 控制方程的离散形式

N-S 方程中质量守恒方程与动量守恒方程分别表示为式（4）与式（5）：

式中：u为流速矢量；g为重力加速度矢量；P为压力项；ρ为流体密度；Γ表示流体黏性力耗散项.

将质量守恒方程改写为SPH离散形式：

式中：下标a表示中心粒子；下标b表示邻域粒子；下标ab表示粒子a与b的差；∇a为针对粒子a的哈密顿算子；m为粒子质量；ρa与ρb分别表示粒子a与粒子b的密度.

通过Favre 平均法对密度进行加权平均，可将SPS 项引入SPH 方法中，动量守恒方程改写为SPH离散形式［16］：

式中：μ0为运动黏度；τij为SPS应力矢量.

2 基于SPH的两相流数值模型

基于SPH 多相流模型的冲刷模拟，通常将泥沙视为非牛顿流体相，常见模型有Bingham 模型［17］、HB（Herschel-Bulkley）［18］模型、HBP（Herschel-Bulkley-Papanastasiou）模型［13］等.此类非牛顿模型在达到屈服强度前后，其表观黏度变化显著：材料所受剪切应力达到屈服强度前，黏度通常较大，流体表现为“难流通”，而在材料屈服后，表观黏度通常急剧下降，逐渐转变为“易流通”，因而适宜模拟冲刷起动前后的泥沙流变行为.然而，Bingham模型及HB模型在低剪切速率时其应力非连续，容易造成数值计算不收敛.本文采用HBP模型建立水-沙两相流模型，将沉积相分为沉积物、推移质、悬移质三种状态，赋予不同流变特性进行计算.

2.1 泥沙相非牛顿流体模型

HBP模型计算流体表观黏度如下：

式中：μori为泥沙表观黏度；μ为黏性系数；n为Herschel-Bulkley 幂指数参数，与剪切应力相关；m为Papanastasiou 参数，控制应力指数增长速率，使应力在未屈服区域保持小剪切速率，在已屈服区域保持线性增长；ⅡD为二阶不变剪切应变率张量；τc为材料屈服强度.

Herschel-Bulkley 模型是广义Bingham 模型，屈服后具有Bingham 模型流变特性，而Papanastasiou 模型适合描述剪切速率趋于0 时材料较大的表观黏度，两模型结合使得HBP 模型在模拟冲刷时稳定性更高，可连续表达土体从低剪切速率发展到高剪切速率的全过程［13］（图1）.此外，当m=0，n=1时，该模型降阶为牛顿流体模型，使得多相流计算中不同流相具有相同广义模型.因而，在DualSPHysics 多相流耦合计算中，对于任意粒子核函数半径内的被检索粒子，仅需基于HBP 模型对所有被检索粒子进行黏性力求解，从而规避了对土体粒子的分类检索计算，简化了计算框架，加快了计算效率［13］.

图1 HBP模型应力曲线随m和n的变化Fig.1 Diagram of the shear stress of HBP model developed with the m and n

2.2 泥沙侵蚀模型

为了模拟泥沙侵蚀与输运过程，本文将泥沙划分为三种状态：沉积物、推移质、悬移质［19］.泥沙粒子状态转化与邻域粒子相关，受其体积浓度、速度及所受剪切应力等因素影响，根据不同状态，赋予不同黏度参与SPH计算.

2.2.1 泥沙屈服强度模型

Drucker-Prager（DP）屈服准则一般形式为：

式中：J2为二阶不变剪切应力张量；p为饱和泥沙粒子上作用的静水压力；α与β由Mohr-Coulomb 屈服准则参数给出：

式中：φ为内摩擦角；c为土体黏聚力.

根据Fourtakas 等［13］的研究，J2可由土粒子所受水体剪切应力ταβ计算：

剪切应力ταβ可由二阶不变剪切应变率张量ⅡD表述：

联立式（11）、式（12）可以建立J2与ⅡD间联系：

进而，|J2|=|αp-β|可作为HBP 模型中材料屈服强度限定条件.计算床面下静止土体屈服强度时，引入Drucker-Prager（DP）屈服准则：

当沉积物粒子所受切应力大小不超过其屈服强度|τy|时，土体粒子由于高黏度特性几乎不发生剪切变形，其表观黏度μapp由|τy|代入式（8）进行计算.

对于河床表面与水接触的土粒子，若满足由沉积物转化为推移质的条件，土体屈服强度采用Shields准则计算并替换，详见2.2.2节.

2.2.2 泥沙起动判定

初始条件下，将泥沙层置于水层下方，当泥沙粒子所受切应力不超过临界值时，泥沙粒子固定不动；达到临界值时，泥沙由沉积物转化为推移质，随水流沿床面输运.

泥沙临界切应力由侵蚀准则计算.Manenti等［12］在冲淤研究中，对Mohr-Coulomb 屈服理论和Shields理论进行了比较分析.研究表明，Shields理论对于模型参数均具有较高敏感性；同时Shields 公式中物理量更易由试验测得，相较Mohr-Coulomb 准则中应变率等参数，计算灵敏度更高，本文最终选择Shields理论作为泥沙状态转化判断准则.

转化为推移质的泥沙粒子须位于河床表面，同时考虑到推移质粒子为饱和土的特性，其转化条件设置以下两个：

1）在泥沙粒子的邻域粒子中，至少包括一个水粒子.

2）待转化泥沙粒子实际质量应小于阈值质量.

当泥沙粒子同时满足以上条件时，基于Shields侵蚀准则，计算水平床面临界转化剪切应力：

式中：τbcr，0为水平床面上的临界剪切应力；d为特征粒径，对于非均匀材料取中值粒径d50；ρs为泥沙饱和密度；θcr为临界Shields数，是泥沙粒子所受临界起动力与最大抗力之比；ρw为水的密度；g为重力加速度.

θcr求解基于雷诺数Re［12］：

式中：R*=，v为水体运动黏度，u*为摩阻流速，按式（17）计算：

根据Prandtl 混合长度理论，假定沉积物表面存在厚度为δ的层流亚层，且流速u(z)按线性分布；在其上紊流层中，流速u(z)按对数分布：

式中：κ为冯·卡曼常数，取0.41；z为水粒子到泥沙-水交界处的垂直距离；z0为床底粗糙度，计算如下：

式中：ks为当量砂径糙率，按经验取泥沙中值粒径.

由式（17）、式（19）可知，摩阻流速u*与δ和z0有关，因此需迭代求解.设定u*初始值u*0从ksu*v＜5的稳态流开始迭代，直至流速曲线u(z)在边界层厚度δ收敛，即u(δ-)=u(δ+)，此时可求得摩阻流速u*，继而求出水平床面的临界剪切应力τbcr，0，以及斜坡修正临界剪切应力τbcr.

水流冲刷的起动力τb由Einstein 对数流速分布公式［20］计算：

式中：d为粒子特征粒径；Δu为泥沙粒子与附近水粒子的速度差，取中心泥沙粒子邻域内所有水粒子进行积分插值：

若泥沙粒子所受剪切应力τb超过临界剪切应力τbcr，则判断泥沙粒子由沉积物转变为推移质.转化后粒子表观黏度需结合HBP模型进行更新，将τbcr代入式（8）中代替屈服应力力τc，计算得到黏度μori.

2.2.3 泥沙上升与沉降判定

已屈服推移质粒子在满足条件时会转化为悬移质，被水流挟带而发生输运.当流速减小、大量悬移质粒子聚集时，悬移质再次沉降，转化为推移质.

悬移质周围泥沙粒子体积浓度Cv，i不超过临界浓度Cvcr：

式中：i表示中心泥沙粒子；j表示邻域粒子；临界体积浓度Cvcr取0.3［12］，当满足式（22）时，泥沙粒子可以作为牛顿流体处理，可以进一步考察流速条件.

引入Mastbergen 公式［21］，计算泥沙临界上升流速与临界沉降流速，如式（23）：

若u≥ulift，则判断推移质转化为悬移质，作为牛顿流体参与计算.其黏度采用Vand 胶体［22］方程计算：

若u≤uset，则判断悬疑质沉降，转化为推移质，黏度按推移质计算.

2.2.4 临界起动切应力斜坡修正

对于任意坡度下泥沙起动分析，需对水平床面临界剪切应力τbcr，0进行修正，得到适用于斜坡的临界剪切应力τbcr.Van Rijn［23］将修正系数分解为纵向坡和横向坡单独影响；Chen 等［24］根据受力平衡推导出任意三维斜坡临界起动切应力修正系数.本文在现有工作基础上，考虑水流升力作用影响，进行临界起动切应力斜坡修正.

假设泥沙粒子为一质点，处于斜坡床面上，其受力包括水下重力W（包含重力与浮力）、水流拖曳力FD、水流升力FL、抵抗起动力FC（本文中即土体的库伦摩擦力）.斜坡、水流方向粒子受力如图2所示.

图2 斜坡床面向量示意图Fig.2 Diagram of the vector of bed surface on the slope

图2中，i、j、k为正交直角坐标系的单位向量；l、t所在平面为斜坡床面，其中l处于XOZ平面，与X轴夹角为α，t处于YOZ平面，与Y轴夹角为β；n为倾斜坡面单位法向量，与Z轴正方向夹角为γ，由几何关系可知cosγ=水流拖曳力FD方向与流速u方向相同.根据Dey［25］的研究，假定水流升力FL方向与坡面法向量n一致，大小与拖曳力比值η为0.85.

水流拖曳力与水下重力沿坡面的分量合成泥沙起动力F：

式中：θx、θy、θz分别为单位向量e与X、Y、Z轴正方向的夹角.

抵抗起动力FC由库伦摩擦力产生，与F方向相反，在极限状态下，

式中：φ表示泥沙内摩擦角.当泥沙粒子达到临界起动状态，即满足

由式（28），推导出|FD|表达式为：

由式（29）得到斜坡床面上的临界起动切应力大小.对于水平床面，通过受力分析易得：

由式（29）、式（30）可得：

式中：k为临界起动切应力斜坡修正系数：

水平面的临界起动切应力经过斜坡修正为

2.3 泥沙模块运行流程

本文冲刷模型中，初始状态下泥沙粒子皆为沉积物，经由每个时间步进行处理，将依次完成沉积物向推移质转化、推移质向悬移质转化以及悬移质向推移质转化.转化完成后，分别存储3 种状态的泥沙粒子，进入SPH 求解步骤，直至计算结束，计算流程示意图如图3所示.

2.3.1 预处理模块

获取上一时间步中泥沙粒子状态信息；迭代计算摩阻流速并应用Shields侵蚀准则得到临界Shields数；按Mastbergen公式计算上升与沉降流速.

2.3.2 推移质模块

沉积物粒子转化为推移质粒子须满足2.2.2 节所述起动条件.因此，需判断其是否处于沙床表面，进而利用Einstein 对数流速分布公式计算该粒子所受流体切应力.若切应力超过屈服应力，则储存为新的推移质粒子，并结合HBP 模型利用Shield 准则计算屈服强度，获得推移质粒子表观黏度.

2.3.3 悬移质模块

推移质粒子转化为悬移质粒子，须满足2.2.3 节所述条件.由于水流裹挟悬移质输送存在浓度阈值，首先判断粒子邻域内泥沙体积浓度，当浓度小于阈值时，判断其速度大小，若速度大于上升流速，则判断为悬移质粒子并依据Vand模型更新粒子黏度.

对于悬移质粒子，其速度若小于沉降流速，则又转化为推移质粒子，返回推移质模块.

2.3.4 沉积物模块

泥沙粒子不起动，基于DP准则结合HBP模型更新其屈服强度.

3 溃坝冲刷数值仿真

SPH 法具有可以模拟流体大变形、复杂液面、不同液相间相互裹挟作用的优势.在两相流冲刷模型中，水-沙相互作用将根据控制方程自动计算，无需单独求解输运方程.本文数值仿真分为两步：①基于DualSPHysics 开源代码进行二次开发，完成泥沙状态转化功能；②进行溃坝水流冲刷模拟，结合水槽试验结果验证数值模型.

需要注意，本节重点对提出的泥沙模块进行验证，对于DualSPHysics 水体计算速度场、压力场和湍流场精确性验证，不在本文的讨论范围内.Sato 等［26］对多种场景下DualSPHysics 流域计算精度进行了验证，限于篇幅，不赘述.

3.1 基于DualSPHysics的冲刷仿真计算流程

本文在DualSPHysics 开源代码的基础上，实现沉积物粒子起动判断与类型转化.二次开发模块分为三部分执行：①初始化模块；②判断模块；③黏度计算模块.程序的运行流程如图4所示.

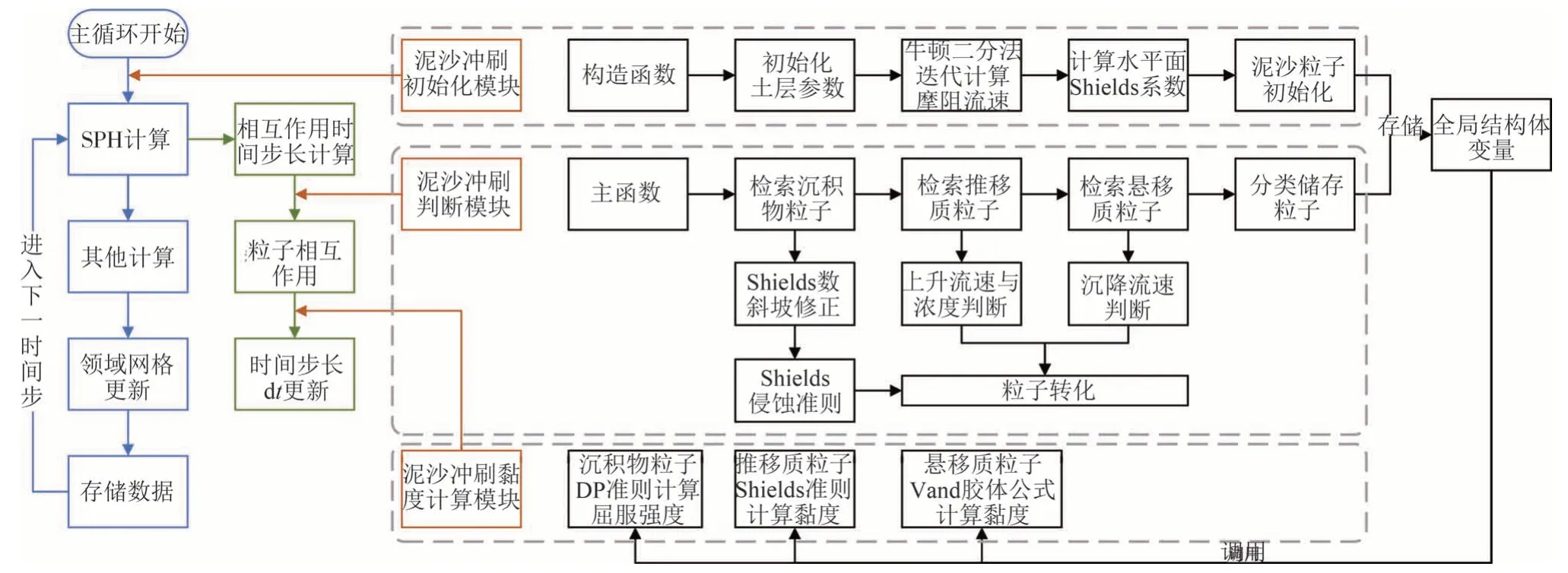
图4 程序运行流程Fig.4 Flow of program executing

针对不同问题与工程条件，本文二次开发模块具有高度可定制性，可根据研究目标灵活地进行土层参数、泥沙起动理论变换.精确捕捉两相流体交界面处粒子黏性与屈服特性，需尽可能提高粒子分辨率，即缩小粒子间距、增加粒子数量.为利用有限计算机资源提高SPH 模拟效率，本文基于CUDA 框架利用GPU 实现泥沙模块加速计算，以解决三维模型对于计算资源要求高的问题.

3.2 数值模型参数设置

Dey［25］在研究黎曼波理论时引用了Louvain 溃坝侵蚀试验，该试验已被多名学者［9，11，27-28］用作冲刷模型评估标准，可为本文提供验证结果.试验中采用长度2.5 m、宽度0.1 m、高度0.35 m的透明水槽，在底部铺满厚度5～6 cm、等效直径3.5 mm、密度1 540 kg/m3的PVC颗粒.试验开始时，通过高速抬升水闸释放高度为10 cm的水柱，并采用高速摄像机记录冲刷过程.

本文三维数值模型水槽宽度设置为0.1 m，在厚度为6 cm、长度为200 cm 的泥沙层上建立深度为10 cm、长度为100 cm的水体.当模拟开始时，水体将迅速跌落，水-沙耦合作用将引起泥沙起动与输送，从而发生溃坝侵蚀.

SPH 法中粒子流速与其设置间距紧密关联，参照Zubeldia 等［19］的研究，通过设置4 组不同间距（0.016 m、0.008 m、0.004 m、0.002 m）模型组别与水槽试验数据分别进行对比，从而确定适宜粒子间距，模型设置如图5 所示.水槽空间布置同溃坝试验相同，长2.5 m，水箱右侧与水槽连接位置（X=0 m）设有0.02 m 开口，水槽底部铺设泥沙，为避免泥沙随水流发生输运，其密度、屈服强度及黏度预设值偏大，可视为固定床面.水粒子动力黏度取1×10-6m2·s，密度为1 000 kg/m3，模型求解时长为8 s.各组别SPH 模型与试验水头在t=8 s 时前进位置绘制如图6 所示.由图6 可知，随着粒子间距不断减小，流体运动模拟结果逐渐逼近真实值.据此建立数值模型，粒子间距取dp=0.002 m，共产生3 087 630个粒子.

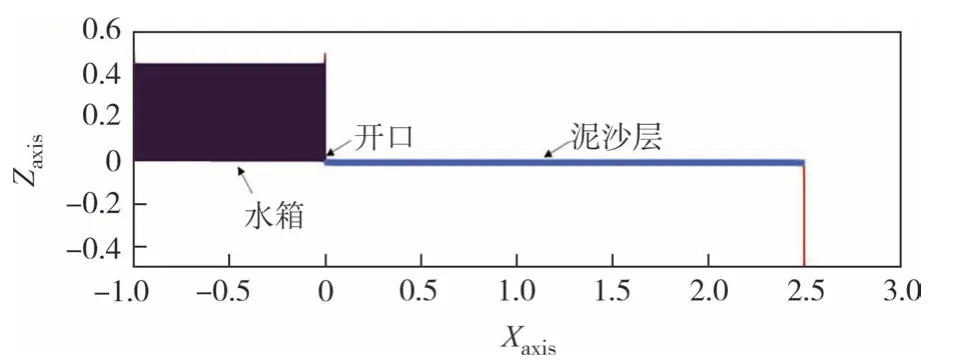
图5 水槽模型示意图Fig.5 Diagram of tank model

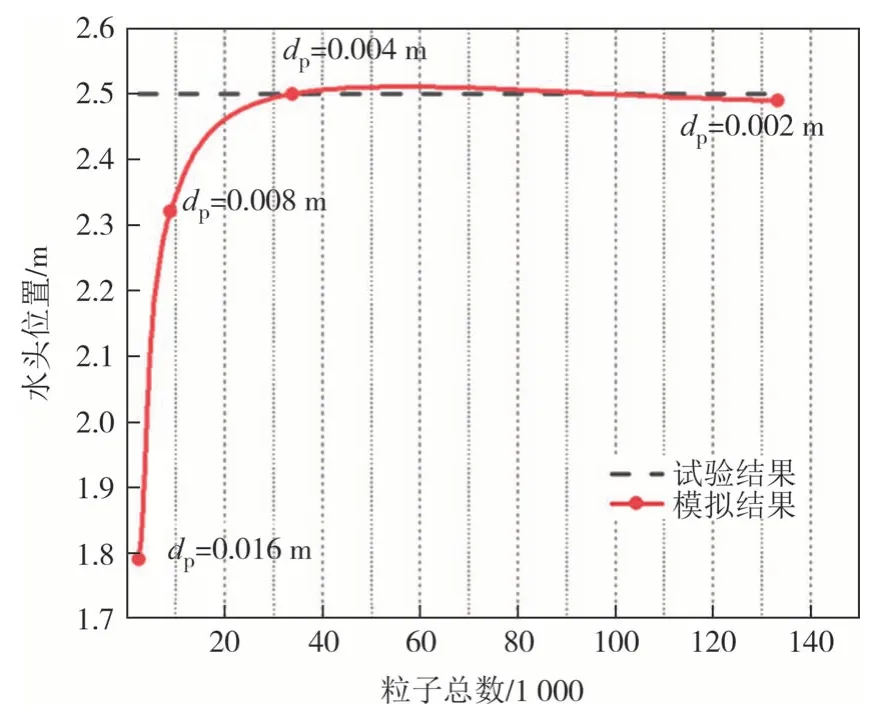
图6 流体粒子间距结果对比Fig.6 Comparison of the distance between particles

泥沙与水的密度分别设置为ρs=1 540 kg/m3和ρw=1 000 kg/m3.泥沙相作为非牛顿流体，参照Fourtakas 等［13］的研究，HBP模型参数取m=100，n=1.8，动力黏度取0.001 m2/s，库伦黏聚力c=0，内摩擦角φ=38°，以模拟物理试验中无黏聚力PVC 材料特性；水作为牛顿流体，取m=0，n=1，动力黏度取1 × 10-6m2/s.沉积物转化推移质质量阈值参照文献［29］取1 250 kg/m3.

3.3 溃坝冲刷形态及误差分析

为验证SPH 法模拟河床冲刷等大变形及强非线性问题的精度优势，本文采用Flow-3D建立相同空间布置网格计算模型，泥沙及水体材料参数设置与SPH模型相同，顶面为压力边界，其余为壁面，采用LES湍流模型，网格尺寸为0.002 m，模型如图7所示.

图7 网格模型示意图Fig.7 Diagram of mesh-model

本次SPH 计算平台为Intel i5-12600KF+NIVIDA 3080Ti，模拟时长为1 s，初始状态模型如图8 所示，求解时间为2 h 22 min.图9、图10 展示了SPH 模型、网格模型与Louvain 溃坝试验在0.25 s、0.50 s、0.75 s、1.00 s 时剖面比较结果，其中：图9（a）为Fraccarollo 物理试验剖面图；图9（b）为本文模拟结果，其中蓝色表示水体，红色表示沉积物；图9（c）为Flow-3D 网格模型模拟结果，其中蓝色为水体，灰色为沉积物.由于篇幅限制，本文仅展示0.25 s 时刻试验及各模型结果.图10 展示了Louvain 试验结果、Fourtakas 模拟结果、本文模拟结果以及网格模型模拟结果的水、沙表面高程对比图，通过计算同一时刻试验与模拟结果液面曲线竖直方向高程均方根误差（ERMS），量化比较两者轮廓线吻合程度.需要注意，在试验与各数值模拟中，水与沉积物均置于三维水槽中，图中展示仅为水槽侧面视图；同时，由于粒子总数量庞大造成其分辨率较高，部分悬疑质粒子紧邻水-沙交界面，影响到真实河床表面高程观测，因此实际河床冲刷后高程应以图10为准.

图8 数值模型示意图Fig.8 Diagram of the numerical model

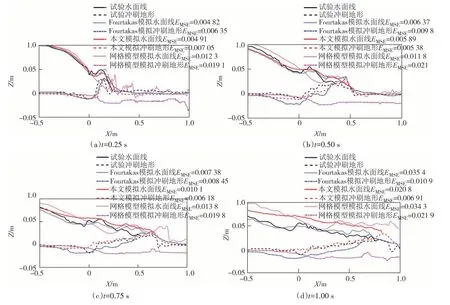
图10 水面及冲刷地形轮廓线对比Fig.10 Comparison of free surface and scour morphology profile

由图9 可知，在t=0.25 s 时刻，本文模型和Fourtakas 模型均能较好地再现Louvain 试验中水头行进位置与形状；水-沙交界面处均较为准确地再现了最大冲刷坑深度与位置.从图9（b）局部放大图中可以看出，交界面处漂移泥沙粒子较多，且受到水流冲击和裹挟作用于近床处发生悬移，河床真实冲刷位置应位于该类粒子下方.本文模型较好地模拟出沉积物泥沙受水体冲蚀发生状态转化，并在水流裹挟下推移、输送，最终沉降、堆积.图9（c）网格模型中河床在水流侵蚀下形成冲刷坑，未再现交界面处水-沙裹挟及水头后方位置泥沙堆积行为，其冲刷坑位置更为靠后，水头模拟误差较大.图10（a）反映出本文模型与Fourtakas 模型总体均方根误差相近，但本文水头行进位置与试验结果更为相符，而网格模型水面线及冲刷地形均方根误差均为SPH模型数倍以上.

在t=0.50 s 时刻［图10（b）］，本文与Fourtakas 模型水头与推移质行进长度均大于试验结果，而本文所得最大冲刷深度相较于Fourtakas模型更为贴近试验结果；网格模型中仍未出现泥沙堆积，仅有冲蚀作用；由高程对比可知，针对自由液面与床沙表面整体形态模拟，本文模型均方根误差均优于Fourtakas 模型，网格模型模拟误差最大.

在t=0.75 s 时刻［图10（c）］和t=1.00 s 时刻［图10（d）］，本文模型自由液面均方根误差略大于Fourtakas 模型，而水沙交界面显著优于Fourtakas 模型，网格模型误差最大.本文模型所得最大冲刷深度略小于试验值.总体上看，相较于SPH 模型，网格模型难以精准捕捉水沙交界面处大变形、强非线性行为，水面及冲刷地形模拟误差均较大.

为进一步对SPH 数值仿真结果的局部误差进行分析，选取坝内断面（S1）、最大冲深位置断面（S2）、Louvain 试验水头处断面（S3）共3处断面对本文模型与Fourtakas 模型模拟误差进行比较，各断面分布汇总如图11 所示.分别提取各时刻两种模型所有断面的自由液面高程及泥沙界面高程，并计算局部误差率绘制成图12.由图12（a）可知，两种模型在水头处（S3）液面模拟误差相比于其他断面均偏大，这与水头推移位置模拟略远于试验结果相关.Fourtakas 模型液面高程整体上略低于本文模型，此种现象是由其河床冲蚀深度整体大于试验结果造成的，河床冲蚀越深使得水位高程相应地沉降越多.本文模型河床冲蚀趋势与试验结果更为贴近，但液面整体上略高于试验结果，推测原因可能为：Louvain 溃坝侵蚀试验采用PVC 塑料颗粒模拟泥沙，而颗粒间存在间隙，随着试验的进行，水流会发生渗流，导致水位下降；Fourtakas 模型与本文模型均采用SPH 方法模拟溃坝冲刷，未能考虑水流向下渗透作用，最终造成本文模型冲刷结果相近而水位偏高的情况，此亦能较好地解释Fourtakas模型冲蚀大于试验结果而水位几乎与试验持平的现象.

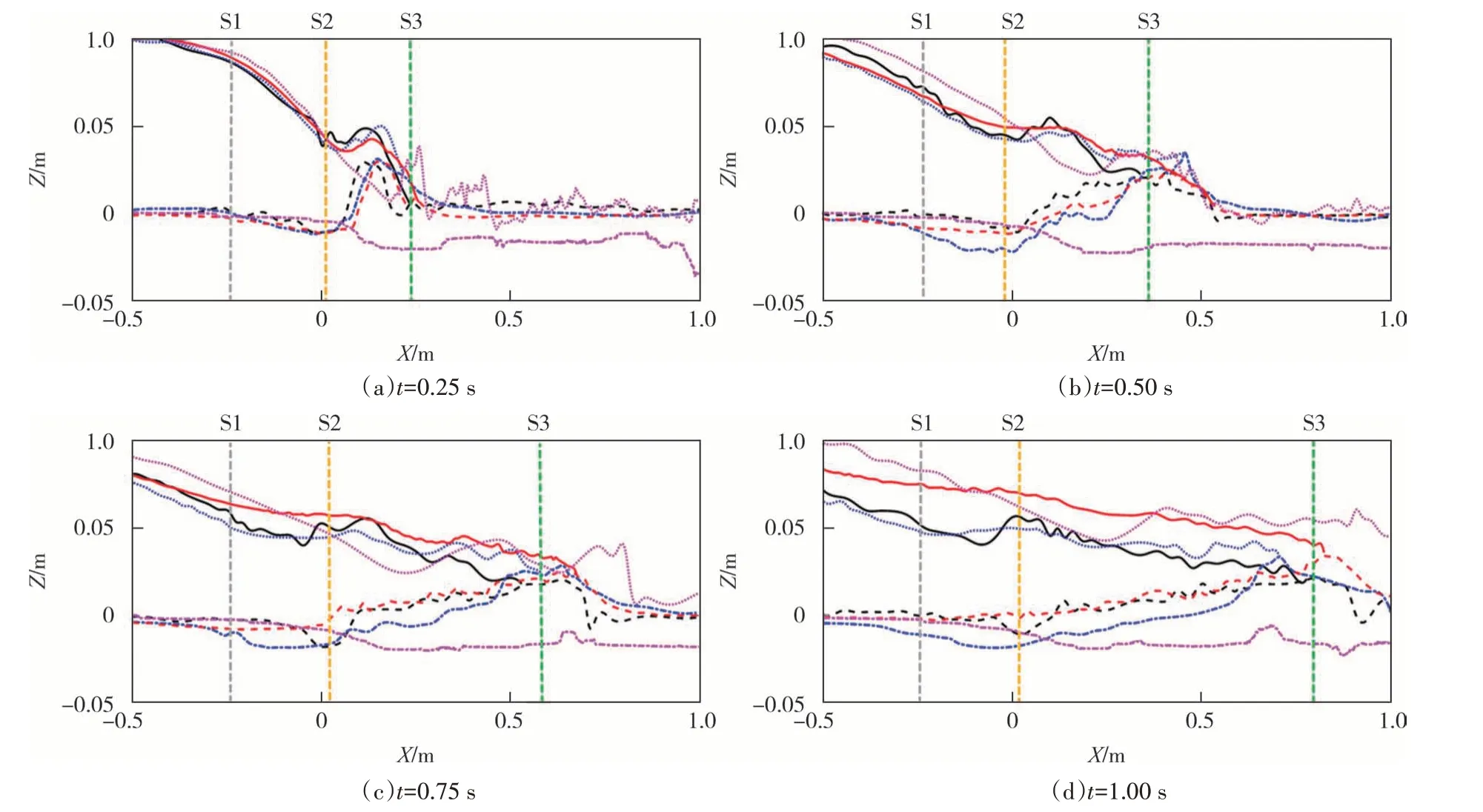
图11 对比断面分布示意图Fig.11 Configuration of the compared sections

图12 误差率变化图Fig.12 Development of percentage of error

图12（b）中S1、S3 断面处泥沙高程模拟，本文模型明显优于Fourtakas 模型，Fourtakas 模型在最大冲深位置前后的模拟误差较大，本文模型改进了这一不足；而各个时刻最大冲深结果，两模型各有优劣.图13 给出了Louvain 试验、Fourtakas 模型以及本文模型最大冲深处高程随时间变化趋势图.由图13 可知，在0.50 s 前，本文模型可以较为精准地预测最大冲刷深度.本文模型和Fourtakas 模型模拟的最大冲刷深度均出现在0.50 s 时刻，而实际最大冲深出现在 0.75 s 时刻；自0.50 s 后，本文模型和Fourtakas 模型最大冲刷深度均出现回升，推测原因为冲刷坑周围泥沙随水流回填至最大冲深处，造成高程回升，而此现象亦在原试验0.75 s 之后发生.整体上看，本文模型所得全过程最大冲深略小于试验值，而Fourtakas 模型略大于试验值.另外，泥沙回填与其流动性相关，最终由其黏度决定，本文泥沙采用HBP 模型，其黏度受m、n值控制，为统一变量从而进行冲刷精度验证，本文参数取值参照了Fourtakas 模型；然而，在本文模型中由于引入了Shields准则作为屈服泥沙强度计算依据，原有模型参数取值可能造成黏度计算误差，从而加剧了冲刷坑泥沙回填现象.事实上，Louvain 溃坝侵蚀试验对照研究中［9，11，13，28］，即使采用相同泥沙本构，也未出现模型参数取值统一，基于SPH 法溃坝冲刷最大深度的精确模拟，仍需在后续研究工作中对泥沙模型及参其数取值深入研究.

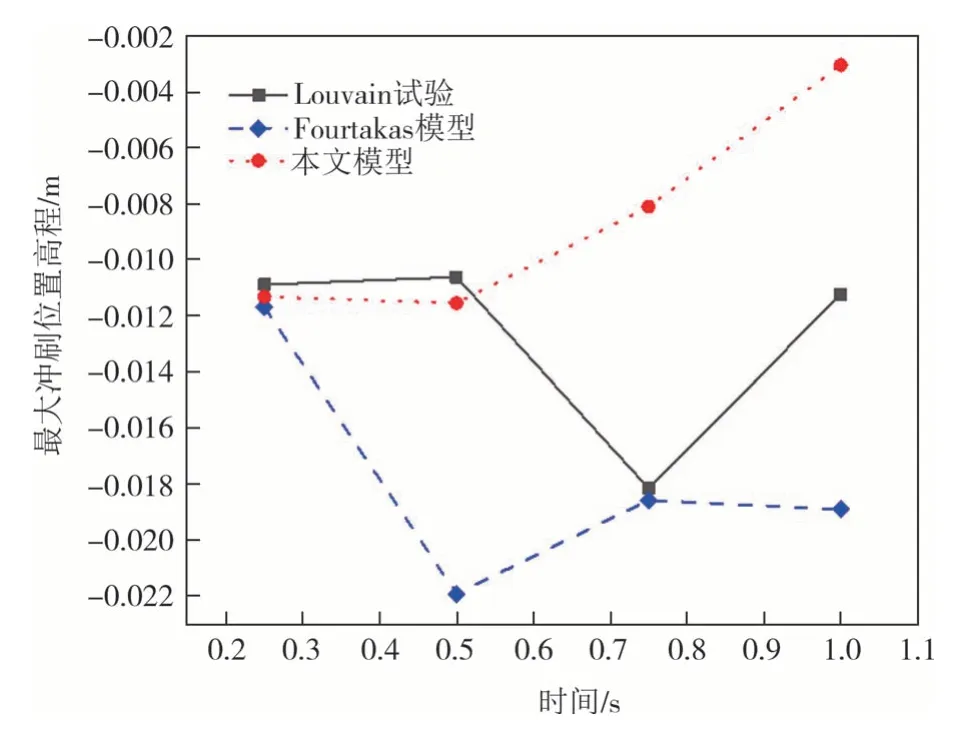
图13 最大冲深位置高程对比Fig.13 Comparison of the elevation of maximum scour position

综上，相比于Fourtakas模型，本文建立的改进模型能够对试验河床整体冲刷形态、演变及推进过程进行更为精确地模拟；两种模型最大冲刷深度与真实结果均存在一定误差.总体上看，使用本文提出的两相流SPH改进算法，仿真计算结果较为可信.

4 结论与展望

1）提出一种基于光滑粒子元的水-沙两相流冲刷数值仿真改进方法.将泥沙视为一种非牛顿流体，引入HBP 模型描述其非牛顿流体行为.根据泥沙运动状态将其划分为沉积物、推移质、悬移质三种类型，引入上升与沉降流速模型作为三种不同状态泥沙转化判断依据.应用Drucker-Prager 与Shields 侵蚀准则计算泥沙起动临界切应力，并为不同状态泥沙粒子赋予不同流变特性.

2）考虑水流升力与水流拖曳力，推导了在三维斜坡床面上泥沙起动临界切应力修正系数，作为水平床面泥沙侵蚀准则的补充.

3）基于所提出的SPH 多相流模型河床冲刷数值仿真改进算法，采用三维溃坝冲刷算例与试验结果以及其他同类仿真结果对比验证模型精度.结果表明，相比于其他同类模型，本文建立的改进模型能高精度模拟试验河床整体冲刷形态、演变及推进过程.

4）当前模型最大冲深与试验结果仍存在一定误差，模型中亦未能考虑水体渗透影响，后续工作将针对上述问题开展进一步研究.