一种结合MADDPG和对比学习的无人机追逃博弈方法

王若冰，王晓芳

（北京理工大学宇航学院，北京 100081）

0 引言

现代无人机体型小，隐蔽性强，大量应用于现代空战。无人机追逃博弈问题成为当前竞相研究的热点。为了提高无人机的自主博弈能力，亟需研究使无人机空战对抗更加智能化的追逃博弈方法［1］。

求解飞行器追逃问题的方法主要有基于蒙特卡洛法的数值求解方法［2］、采用最优控制理论［3-4］和微分对策理论［5-6］的方法。采用数值解法的追逃博弈求解方法需要进行大量仿真，求解成本过高，不满足当前快速求博弈均衡解的需求。文献［3-4］在基于最优控制理论的飞行器追逃博弈求解方法中，都假设对方的机动策略已知。这些方法不适用于追逃双方均在自己最大机动能力范围内进行机动，而没有哪方采用固定策略的场景。采用微分对策理论的博弈方法大多是基于精确的追逃双方相对运动模型推导的。而现代战争中，复杂战场环境往往对飞行器形成较大干扰，无法建立其追逃问题的精确数学模型，此时微分对策博弈方法的精度将会下降，甚至不再适用。

近年来发展起来的深度强化学习算法不需要建立飞行器的精确数学模型，而是通过与环境的交互、设定奖励函数来引导飞行器进行自主机动决策。当前，深度强化学习算法在航迹规划［7］、制导律设计［8-10］、姿态控制［11-13］、空战决策［14］等多方面有着较多的应用。近年来，也有学者采用深度强化学习理论研究飞行器追逃博弈问题［15-16］。文献［15］采用基于自博弈架构的PPO 算法，根据CW 方程设计了一种特殊的奖励函数，最终求解得到轨道航天器追逃博弈的均衡解；文献［16］将模糊推理与时序误差评价相结合，对经验回放池进行分类后，采用深度强化学习算法求解了高速飞行器的攻防博弈。

当前采用深度强化学习算法的追逃博弈求解方法，大多采用了多阶段交替训练（自博弈）的方式，也就是固定一方的策略同时训练另一方的策略直至收敛，并进行多次交替训练。但实际博弈过程中，追逃双方同时机动，上述方法求得的解并不一定是最优解，且该方法中网络的训练时间比较长。本文将复杂作战环境中变速飞行的飞行器追逃博弈问题看作多智能体博弈对抗问题，采用多智能体强化学习与博弈论相结合的方法，通过“集中式训练、分布式执行”［17］的方式，实现训练过程中无人机追逃双方的同时机动博弈，在追逃双方奖励函数收敛时求得双方的最优解（纳什均衡解）。

在追逃博弈问题中，捕获域和逃逸域是非常重要的概念。所谓捕获域是指追击方成功情况下追逃双方初始态势的集合，逃逸域定义类似。目前求解捕获域（逃逸域）的方法，大多数是在定性或定量微分对策的基础上，对微分对策问题进行简化，最后求得捕获域［18-19］。文献［18］采用微分博弈理论研究了捕获域的存在条件，并给出了近地轨道飞行器追逃博弈中关于偏心率的捕获域边界；文献［19］提出了一种基于定性微分博弈的数值方法，对轨道追逃问题中的三维界栅轨迹和捕获域进行转化并求解。

以上求解捕获域的方法都是在精确数学模型基础上进行的，当飞行器处于复杂干扰环境而无法获得精确数学模型，求解捕获域非常困难，目前还未见到此方面的文献。事实上，影响博弈结果的初始因素很多，例如初始位置、初始速度方向等，故表征捕获域的是一个高维状态向量域，此时捕获域的求解会更加复杂。深度对比学习方法是一种考察样本之间差异信息的监督学习方法［20-21］，通过构建孪生神经网络，采用引导样本进行分类的损失函数训练出一种可以稳定有效提取特征的深度神经网络。而捕获域和逃逸域实际上是两种不同类别的高维向量域，因此本文采用深度对比学习的方法，对高维初始状态向量进行区分学习，进而实现对复杂环境中高维捕获域（逃逸域）的间接表征。

1 问题描述与建模

1.1 无人机运动建模

假设两架无人机在水平面内进行博弈对抗，其相对运动关系如图1所示。

图1 无人机二维追逃博弈几何模型Fig.1 Geometric model of UAVs two-dimensional pursuit-evasion game

图1 中，OXZ为地面坐标系。P、E 分别代表追击方无人机（以下简称“追击方”）和逃逸方无人机（以下简称“逃逸方”）。vP、vE分别为追击方和逃逸方的速度矢量，速度矢量与OX轴的夹角为速度方向角ψ，若由OX轴逆时针旋转至速度矢量，则ψ为正，反之为负。ηPE为追击方速度矢量前置角，即vP与目标视线之间的夹角，若由速度矢量逆时针旋转到目标视线，则ηPE为正，反之为负。分别为追击方和逃逸方的切向加速度大小则为双方的法向加速度大小。qPE为追击方-逃逸方无人机视线角。

考虑扰动的无人机运动模型为：

式中：xi，zi(i=P，E)为无人机i的质心坐标和为复杂环境中的等效有界扰动。考虑到无人机机动能力的有限性，其控制量须满足：

在无人机追逃博弈问题中，无人机i可通过携带的惯导、雷达探测器等装置获得自身与对手的位置以及自身的速度信息，故可得双方之间的距离rPE及追击方速度矢量前置角ηPE为：

式中：vP、rPE分别为追击方速度大小与追逃双方相对距离大小。

假设ra为追击无人机的毁伤半径，Tmax为考虑燃油等因素的无人机允许飞行最长时间。当满足以下不等式时，认为追击方成功捕获逃逸方，否则认为逃逸方成功逃逸。

式中：TPE为追逃博弈的实际时间。

1.2 无人机追逃博弈数学建模

对于无人机追逃博弈问题，追击方与逃逸方是非合作目标，双方的博弈目的完全冲突，此问题实质上是一种完全竞争的零和博弈（Zero-sum game，ZSG）问题。二维平面内运动的无人机通过调整切向加速度和法向加速度来实现对运动的控制，即无人机i的控制量ui=

追逃博弈过程中，追击方（逃逸方）在考虑对方的前提下，不断调整自身的策略以缩短（增加）相对距离来实现捕获（逃逸）。根据追逃双方上述博弈目标，构建t时刻基于相对距离的博弈效能微分函数jP(uP，uE)、jE(uP，uE)，考虑总博弈时间为TPE，则时间-控制量效能目标函数为：

式中：λi(i=P，E)为加权系数。

综上，本文的无人机追逃博弈三要素为：博弈者集合{P，E}、动作集合U={uP，uE}、效能函 数{JP，JE}。

在无人机追逃博弈过程中，追逃双方分别根据当前的状态调整策略，独立优化各自的效能函数JP，JE，并得到各自的最优策略。假设目标函数JP，JE：uP×uE→R在uP×uE上连续，则根据博弈论中的纳什均衡理论，双方的策略满足如下不等式时，零和博弈存在纳什均衡态：

式中：J=JP。对于零和博弈，博弈均衡态是博弈系统的稳定状态。本文采用的基于多智能体强化学习算法的无人机追逃博弈求解框架，在“集中式训练”中，追逃双方的博弈能力不断提升，最终双方的效能函数均达到考虑对手策略与状态下的最优，系统到达博弈纳什均衡态。采用“分布式执行”的方式，追逃双方可根据自身状态执行将所有对手的状态与动作考虑在内的纳什均衡策略，得到在不同初始条件下的纳什均衡解。

2 采用MADDPG算法的追逃双方纳什均衡解求解

MADDPG 算法基于多个智能体之间的博弈关系，采用全局观测信息与策略不断评估各个智能体的决策。本节首先介绍多智能体马尔科夫决策过程与MADDPG 算法理论，最后给出了采用MADDPG 算法的无人机追逃博弈纳什均衡解求解流程。

2.1 追逃双方多智能体马尔科夫决策过程

2.1.1 追逃双方的状态空间与动作空间

对于多智能体强化学习，其采用的马尔科夫决策过程可以看作一种随机博弈（Stochastic games，SG）框架，具体可以表示为：

式中：S为包含环境中所有智能体的所有状态的空间集合，在无人机博弈问题中，观测量S为：

设N为参与博弈的智能体数量，A1，A2，…，AN表示各智能体的动作，则多智能体的联合动作A可表示为A=A1×A2× …×AN，对于无人机追逃博弈，无人机i(i∈{P，E})的动作为其切向加速度大小ati和法向加速度大小ani，则联合动作A为：

式（8）中的P：S×A×S→[0，1]为状态转移矩阵，γ∈[0，1]为奖励期望中的衰减因子。

2.1.2 追逃双方的奖励函数

式（8）中，R1，R2，…，RN为智能体的即时奖励。奖励函数的设置对于MADDPG 算法的收敛性具有重要影响。追逃博弈过程中，式（3）中的相对距离rPE与追击方速度矢量前置角ηPE对追逃双方的博弈态势有着至关重要的作用，因此可根据这2 项设定奖励函数。

式（14）中：ηa为追击方期望的速度矢量前置角，为了有利于追击目标并且网络不至于太难收敛，其一般设为一个较小的值，本文设为15°。

为了避免常值奖励函数带来的奖励稀疏问题，式（11）～（14）中，在常值奖励函数的基础上增加了随时间变化的项（式（12）和（14）的常值奖励函数可看作0）。

综上，对于第m步，追击方奖励函数RP为：

类似地，逃逸方的奖励函数RE也由4 部分组成：

考虑到逃逸方目标与追击方相反且采用零和马尔科夫博弈的前提，式（16）中4 部分奖励函数分别为：

2.1.3 无人机追逃博弈的纳什均衡态表征

追逃双方无人机智能体i(i∈{P，E})的状态值函数为：

式中：πi为智能体i的策略，π-i为除去智能体i以外其他智能体的策略；Ei表示智能体i的累计回报在联合状态St=T=s处的期望值为智能体i在t=T+1 时刻获得的奖励；St=T+1为所有智能体在t=T+1时刻的联合状态集；γ仍然为折扣系数。

对于无人机追逃博弈这个零和博弈问题，所有智能体i(i∈{P，E})都在最大化各自的策略价值函数，其纳什均衡态可表示为：

式中：πi，∗、π-i，∗分别为智能体i与除去i外的其他智能体的纳什均衡策略；∏i为智能体i的策略集。

2.2 MADDPG算法框架

MADDPG 算法的网络结构分为Actor 网络与Critic 网络，其采用“集中式训练，分布式执行”的框架进行训练，意义在于：在训练过程中，通过全局集中式的Critic 网络对各个独立的agent 进行训练，使得每个agent 都在考虑全局信息的前提下对自身的局部策略进行调整，避免了单智能体算法无法解决的环境不平稳问题；在分布式应用时，每个Actor 网络仅需根据自身的观测信息便可得出策略。

采用MADDPG 算法的无人机追逃博弈求解算法架构如图2所示。

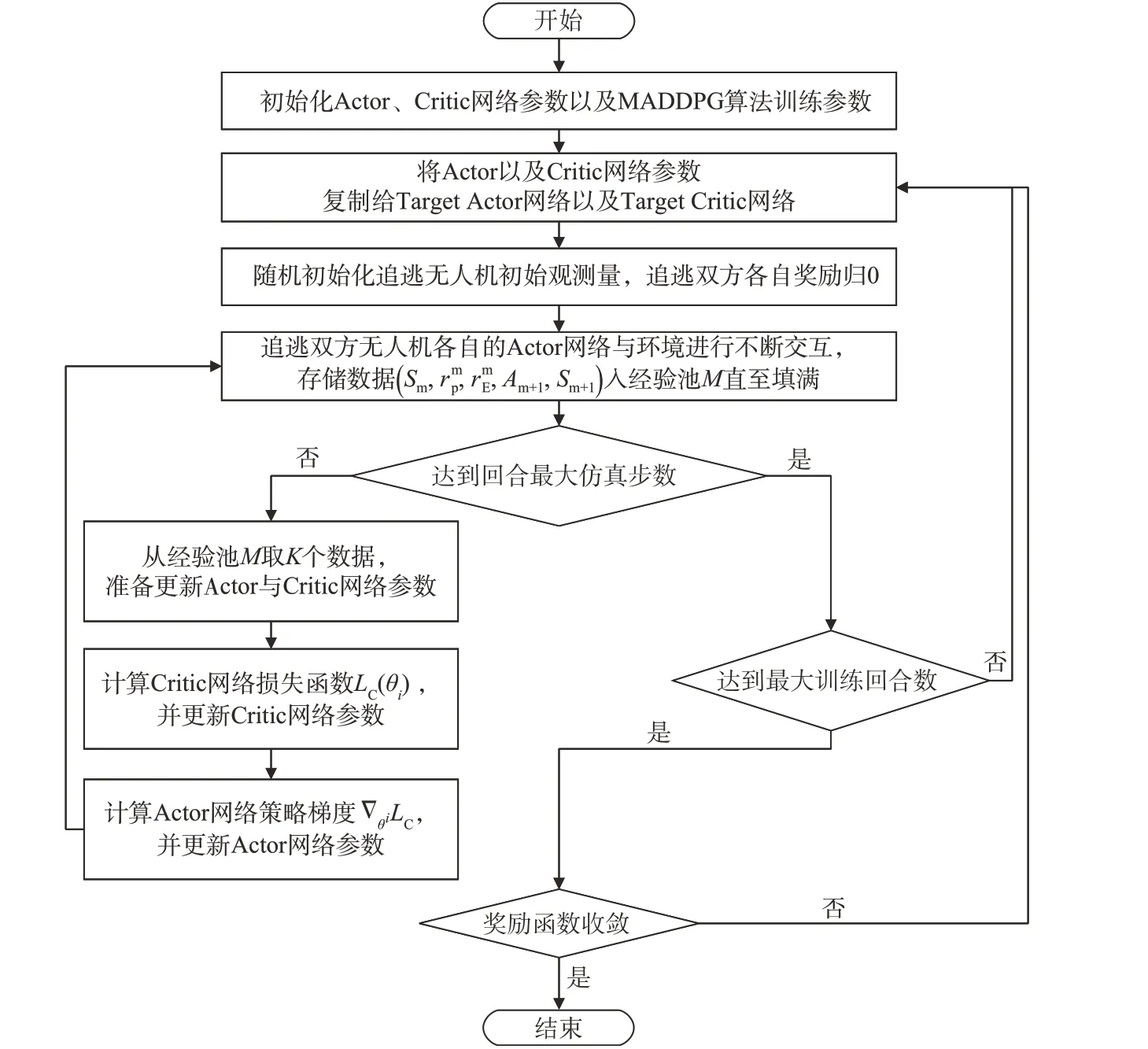
图2 采用MADDPG算法的无人机追逃博弈求解算法架构Fig.2 Framework of the MADDPG algorithm solving the pursuit-evasion game between UAVs

多智能体追逃博弈网络中，每个智能体的Critic网络的输入包括所有智能体的全局信息，网络损失函数为：

Critic 网络通过最小化式（20）来实现自身网络参数的更新。

追逃双方智能体的Actor 网络则采用梯度下降法进行参数更新，每个智能体的Actor网络仅需要局部信息，以此实现后续的分布式执行。

智能体(i∈{P，E})的Actor 网络梯度的计算公式为：

式（20）～（21）中，参数上下标t代表更新网络参数的第t个数据，其中t=1，2，…，K。

追逃双方的Actor网络参数的更新公式为：

式中：η为学习率，θi为Actor网络参数。

在MADDPG 集中式训练过程中，追逃双方智能体i(i∈{P，E})的策略梯度均按照式（20）～（22）进行更新。当每个智能体的奖励函数都趋于收敛时，双方的奖励均为考虑对手策略下的最优，根据1.2小节以及式（6）可知，此时便得到了多智能体追逃博弈的纳什均衡解。

2.3 对比学习下的追逃双方捕获域和逃逸域求解

2.3.1 无人机捕获域和逃逸域的表征

对于无人机追逃博弈，双方的博弈结果取决于博弈的初始态势，即不同的初始状态对应的双方博弈结果不同。本文中，定义追击方成功捕获所对应的追逃双方初始条件的集合为捕获域；逃逸方成功逃逸所对应的初始条件的集合称为逃逸域。

若对抗开始时，追逃双方的位置、速度大小已定，则表示初始速度方向的速度方向角组合(ψP0，ψE0)可表征捕获域和逃逸域；若对抗开始时，追逃双方的速度大小和方向已定，则双方的初始位置XPE=(xP0，zP0，xE0，zE0)T可表征捕获域和逃逸域。

以(ψP0，ψE0)表征的捕获域（由于逃逸域也类似，以下均不再写逃逸域）是二维平面内的点集，因此可较容易地直观表征。而以(xP0，zP0，xE0，zE0)T表示的捕获域为四维点集，其表征比较困难。如果对抗开始时双方的位置和速度均未定，则表征捕获域的向量维度更高。本文采用对比学习的方法来求取高维捕获域。

对比学习通过让孪生神经网络学习数据点之间的相似或不同的关系，来获得区分数据点类别的能力［21］。对于高维度的向量，孪生神经网络将其映射为一个具有区分度的低维向量，并通过衡量低维向量之间的相似度来衡量高维向量之间的相似度。

对于本文中的高维捕获域与逃逸域，两者互不相容，故可采用对比学习的方法，利用孪生神经网络将高维初始条件映射为具有区分度的低维特征向量，并衡量低维特征向量的相似程度，进而对高维的捕获域和逃逸域进行间接表征。

2.3.2 深度对比学习的样本集获取

给定典型攻防对抗场景下的初始条件，采用收敛的MADDPG 博弈网络获得不同初始态势下的博弈结果，从而获得捕获成功样本点集和逃逸成功样本点集。之后，采用先随机打乱、后随机取样的方式获得具有相同分布且互不相容的训练样本集、验证样本集与测试样本集，用于孪生神经网络的训练和测试。

2.3.3 采用深度对比学习的捕获域求解

孪生神经网络的2 个输入为追逃博弈的2 个初始条件X1，X2，以Y来表示X1，X2的差异 度。若X1，X2对应的博弈结果相同，称其为同类样本对，则Y=0；若不同，则为异类样本对，同时Y=1。孪生神经网络由2 个共享权重的深度神经网络构成，输入为高维的向量样本对X1，X2，输出为具有可提取特征的低维样本对G(X1)，G(X2)。X1，X2之间的相似程度用映射后的低维向量之间的欧氏距离D来衡量，即：

设定欧氏距离阈值ε，当D(X1，X2) ≤ε时，认为X1，X2相似；反之，则认为X1，X2相异。对比学习算法通过低维样本的相似度衡量高维向量的相似度，具体见文献［21］。

孪生神经网络的损失函数为对比损失函数L，其表达式为［21］：

基于训练集中的同类样本对与异类样本对，通过最小化L来不断更新网络参数，最终可训练出使异类样本对相互远离，同类样本对相互靠近的孪生神经网络。当L趋于0 并稳定后，认为孪生神经网络收敛，此时网络便具有了稳定地提取特征的能力。

设孪生神经网络提取特征能力的强弱由区分正确率ζ来表示：

式中：N为总样本数，M为孪生神经网络区分正确的样本数。

本文采用对比学习算法，在训练过程中通过L来调整网络参数，直到验证集与训练集的ζ均不低于95%且L收敛时，停止训练。再应用测试集对该网络的区分效果进行非重复试验，进而验证网络对样本区分的有效性与鲁棒性。

3 仿真校验及分析

3.1 仿真条件

本仿真在CPU 为i5-6500 CPU@3.20 GHz、内存为12 GB 的PC 机上进行，基于Pycharm Community 2022.03.22 平台、采用Python 3.7 语言进行程序编写，深度学习环境采用Pytorch 1.13.1。

追逃双方无人机的初始位置、初始速度大小及方向范围、双方的切向和法向加速度范围，以及扰动见表1。表中dti与dni在扰动范围内均匀分布。

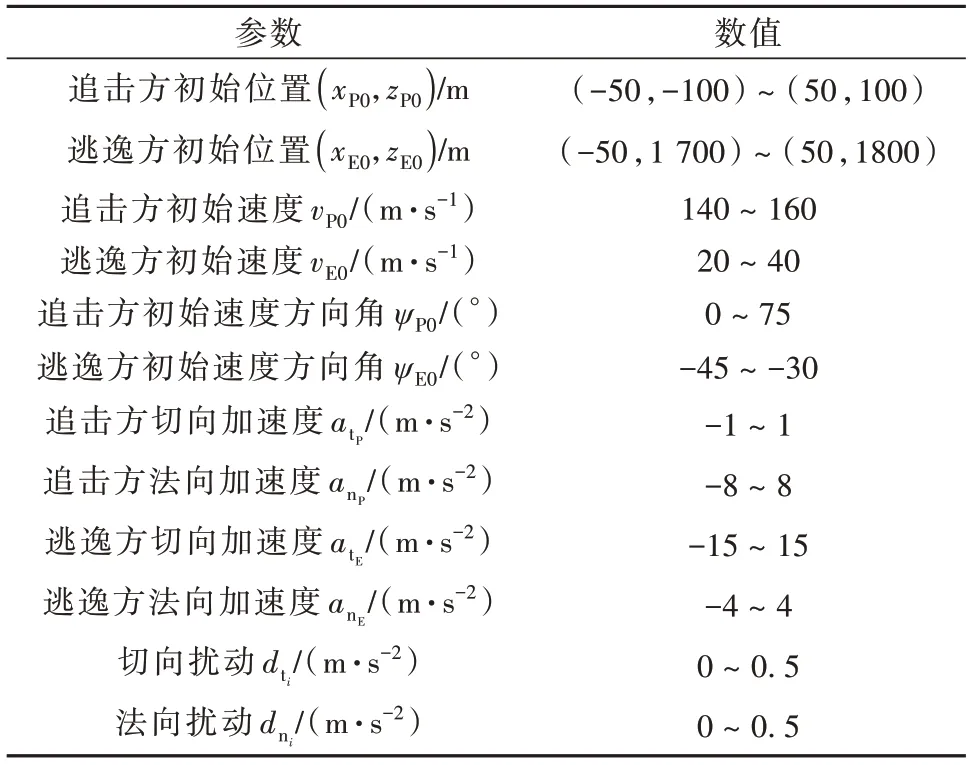
表1 追逃双方初始参数、加速度及扰动Table 1 The initial parameters，accelerations of the pursuer and escaper and the disturbances

假设追击方无人机毁伤半径ra=15 m。MADDPG 算法中的Actor 网络与Critic 网络的参数设置见表2。

表2 MADDPG网络参数Table 2 Network parameters of MADDPG

MADDPG算法训练参数设置见表3。

3.2 无人机博弈对抗纳什均衡解求解分析

采用表2～3 的网络与算法参数，对处于表1 随机场景中的追逃双方无人机进行集中式训练，得到的追逃双方平均回合奖励如图3所示。

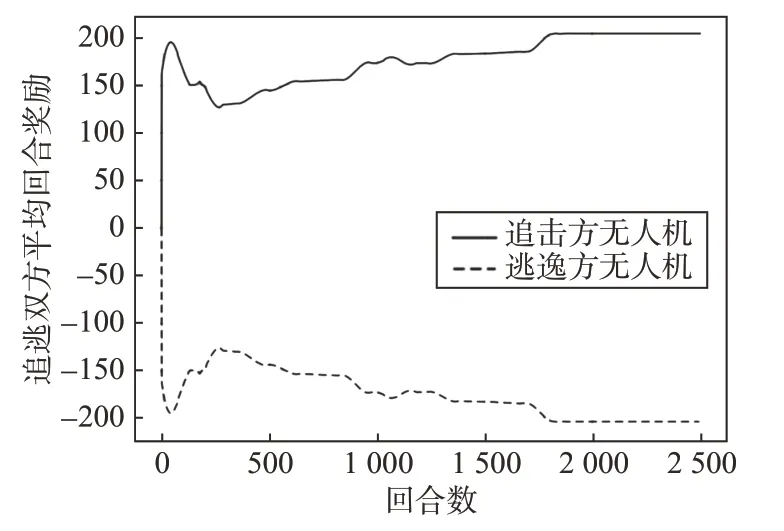
图3 追逃双方平均回合奖励Fig.3 Average episode reward of the pursuer and escaper

由图3可知，博弈对抗网络在经过1 849回合的集中式训练后，追逃双方平均回合奖励趋于收敛，此时双方的奖励函数都在考虑对方策略的前提下趋于收敛稳定，系统达到了均衡状态，此时博弈对抗网络即为纳什均衡网络。

采用收敛的MADDPG 博弈对抗网络作为策略生成网络，对给定追逃双方初始条件的场景进行“分布式执行”，实现双方无人机的博弈对抗。假设某作战场景中，追击方的初始位置(xP0，zP0)为（-30.84，24.42）m，初始速度大小vP0=148.75 m/s，初始发射方向ψP0=69.13°；逃逸方初始位置(xE0，zE0)为（27.99，1 727.25）m，初始速度大小为vE0=24.42 m/s，初始发射方向ψE0=-34.68°。追逃双方切向、法向加速度范围与训练时相同，见表1。

采用MADDPG 决策网络得到追逃双方的飞行轨迹（包含第20、30、40步的追逃双方实时位置和视线）如图4所示。

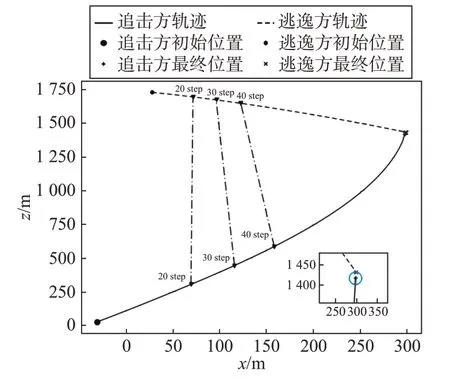
图4 追逃双方运动轨迹Fig.4 The trajectory of the pursuer and the escaper

由图4可知，在给定场景中，追击方在t=9.809 s时与逃逸方的相对距离rPE达到15 m，实现了对逃逸方的捕获。

追击方和逃逸方的切向加速度、法向加速度变化如图5～8所示。

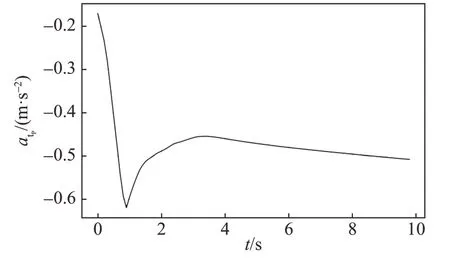
图5 追击方切向加速度Fig.5 The tangential acceleration of the pursuer

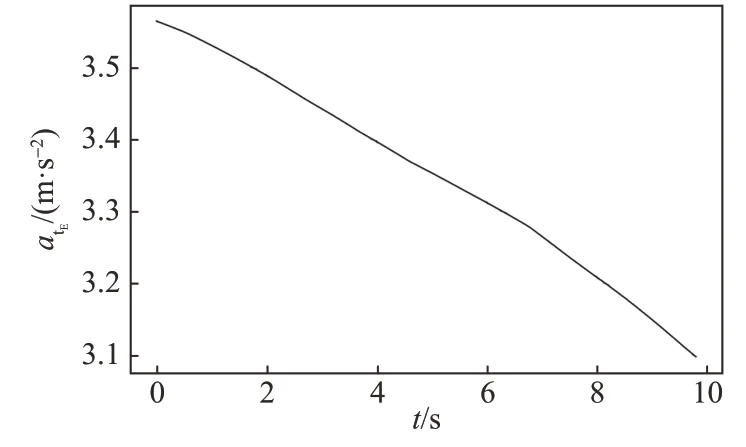
图6 逃逸方切向加速度Fig.6 The tangential acceleration of the escaper

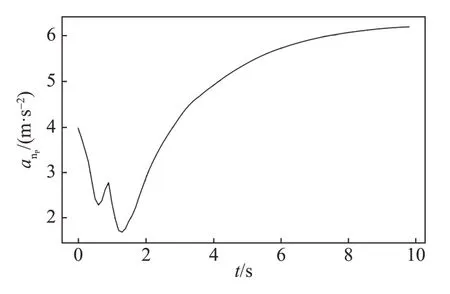
图7 追击方法向加速度Fig.7 The centripetal acceleration of the pursuer

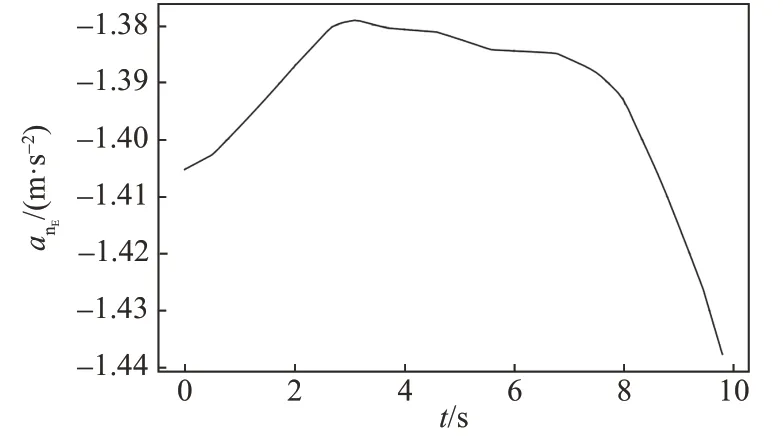
图8 逃逸方法向加速度Fig.8 The centripetal acceleration of the escaper

由图5～8可知，追击方的切向加速度较小且其变化也较小，而其法向加速度变化较大；逃逸方的法向加速度较小且其变化也较小，但其切向加速度较大，因此追击方主要通过法向机动进行追击而逃逸方主要通过切向机动进行逃逸。

对于无人机追逃博弈，不同的初始条件下，追逃双方的博弈结果也不同，接下来求解以初始发射方向、初始位置表征的捕获域和逃逸域。

3.3 无人机追逃博弈捕获域与逃逸域求解

1) (ψP0，ψE0)表征的捕获域与逃逸域

假设追逃双方的初始位置、速度大小以及加速度范围与3.2 中的仿真场景一致，追击方、逃逸方的初始速度方向角ψP0与ψE0分别在[60°，75°]和[ -45°，-15°]内采样。采用收敛的MADDPG 决策网络作为无人机的控制网络，根据博弈结果，可直接通过蒙特卡洛打靶的方式得到以(ψP0，ψE0)表征的捕获域和逃逸域，具体如图9所示。

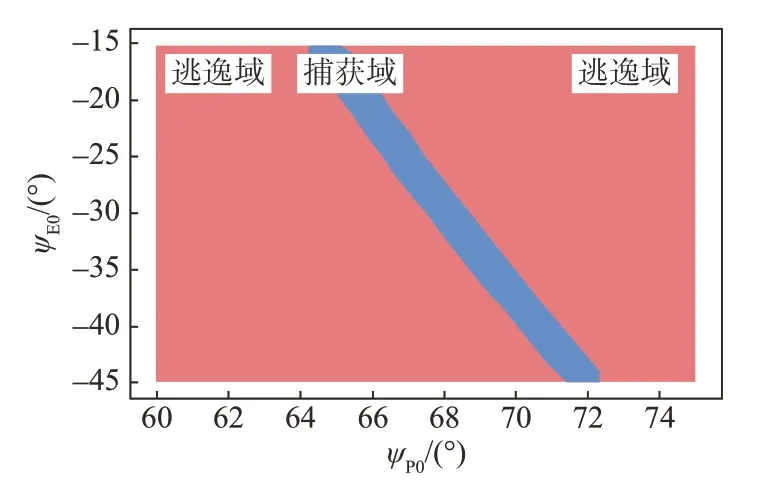
图9 捕获域与逃逸域的划分Fig.9 Division of capture region and escape region

图中，蓝色区域为捕获域，红色区域为逃逸域，分别表征追击方成功捕获与逃逸方成功逃逸的(ψP0，ψE0)。

2) (xP0，zP0，xE0，zE0)表征的捕获域与逃逸域

假设追逃双方无人机初始速度大小及加速度范围同3.1 中的仿真场景，本部分设双方的初始发射方向分别为ψP0=60°，ψE0=-30°。追击方初始位置的xP0、zP0分别在（-100，0）m 和(0，100) m 内均匀采样，逃逸方初始位置的xE0、zE0分别在(0，100) m 和(1 700，1 800) m内均匀采样。将四维向量XPE=[xP0，zP0，xE0，zE0]T输入MADDPG 博弈对抗网络，根据博弈结果，划分同类样本对与异类样本对，2类样本对的数量基本符合1∶1 的比例。2 类样本对混合得到总样本对集合W。基于W按照8∶2∶2的比例划分训练集T、验证集V和测试集J，各样本集中同类、异类样本对的数量也基本符合1∶1的比例，具体见表4。

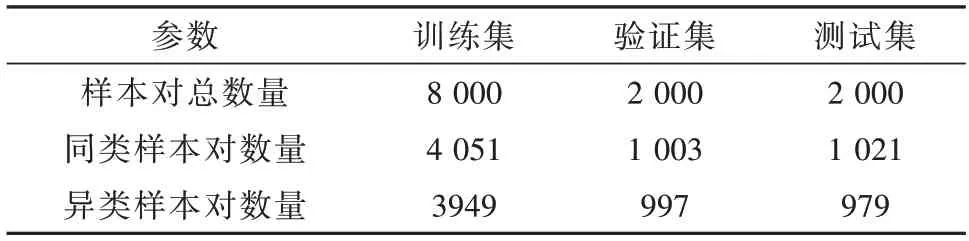
表4 训练集、验证集和测试集参数Table 4 The parameters of the training set、validation set and test set

对比学习训练参数以及孪生神经网络结构参数设置见表5。

表5 对比学习训练参数和孪生神经网络参数Table 5 The training parameters of contrastive learning and parameters of the Siamese Network

在计算区分正确率的式（25）中，设N=100。在表4和表5的基础上，得到孪生神经网络的L随回合数变化曲线如图10所示；训练集与验证集的区分正确率随回合数变化的曲线如图11所示。

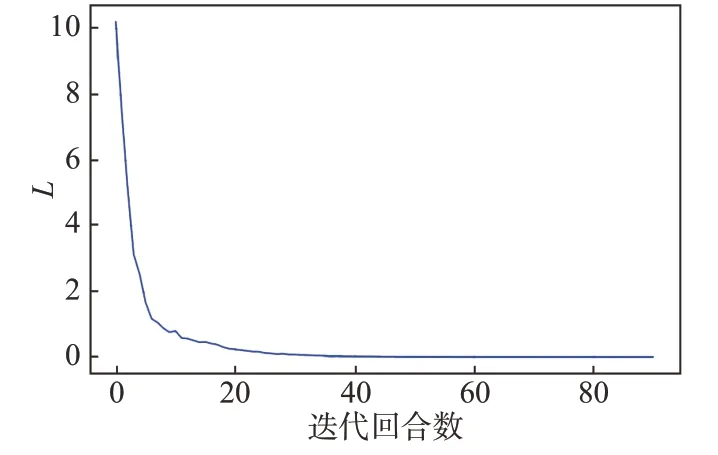
图10 孪生神经网络的损失函数图Fig.10 The loss of the Siamese Network

图11 训练集与验证集的区分正确率Fig.11 The distinguish accuracy rate of the training and validation set

由图10 可知，经过40 回合的训练后，孪生神经网络的L逐渐收敛至0附近；由图11可知，随着回合数的增多，训练集和验证集的区分正确率呈现振荡上升趋势，当回合数为90 时，测试集和验证集的区分正确率均达到96%，此时满足算法终止条件（区分正确率大于95%），停止训练。

从测试集中随机抽取100 个样本对，采用第90 回合的孪生神经网络对其进行判别，重复进行30 次。在30 次的测试结果中，最低的ζ为88%，最高的ζ达99%，平均ζ为94.8%，说明训练出的孪生神经网络对于追击成功与逃逸成功对应的高维初始条件有着较强的区分能力。

随机从W中抽取1 414 个高维样本（追击成功、逃逸成功样本分别为621、793个），将其输入至孪生神经网络，根据深度对比学习算法的原理，网络将输出具有可区分特征的低维向量，其空间分布如图12所示。

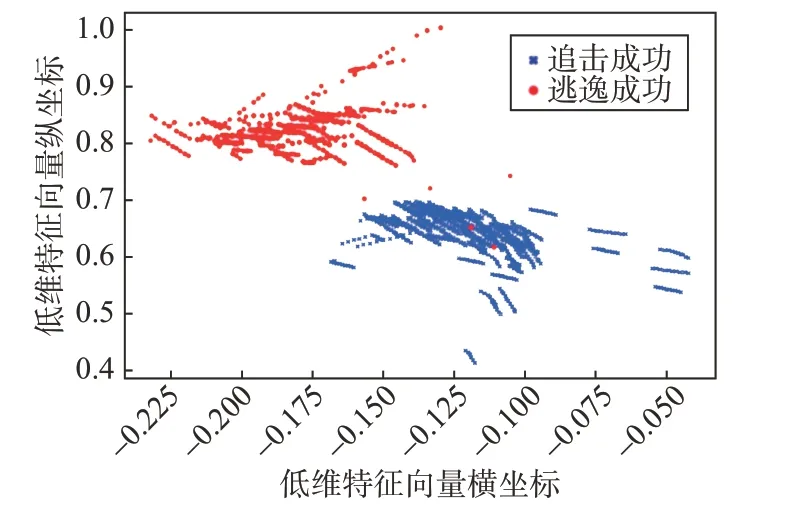
图12 追击成功与逃逸成功的低维可提取特征向量分布Fig.12 Low-dimensional extractable feature vector distribution of successful pursuit and successful escape

由图12可知在绝大多数情况下，经由对比学习得到的孪生神经网络可将追击成功与逃逸成功的高维向量对应的低维特征向量明显地区分开，即：同类样本点的低维特征向量之间的距离大部分小于欧氏距离阈值0.1，异类样本点的低维特征向量之间距离则大部分大于0.1。结合式（24）可知，孪生神经网络使同类样本点相互靠近而异类样本点相互远离，以此实现了对于高维初始条件的区分，进而间接表征了高维捕获域。

在实际应用时，令孪生神经网络的其中一个输入为捕获成功的某初始条件向量(xP0，zP0，xE0，zE0)T=（-50，40，90，1 790）Tm，另一个输入是需判别的20个初始条件向量，得到的对比学习分类与实际分类结果如表6所示（为了节省篇幅，只给出其中10个的结果）。表中P和E分别表示捕获成功和逃逸成功。

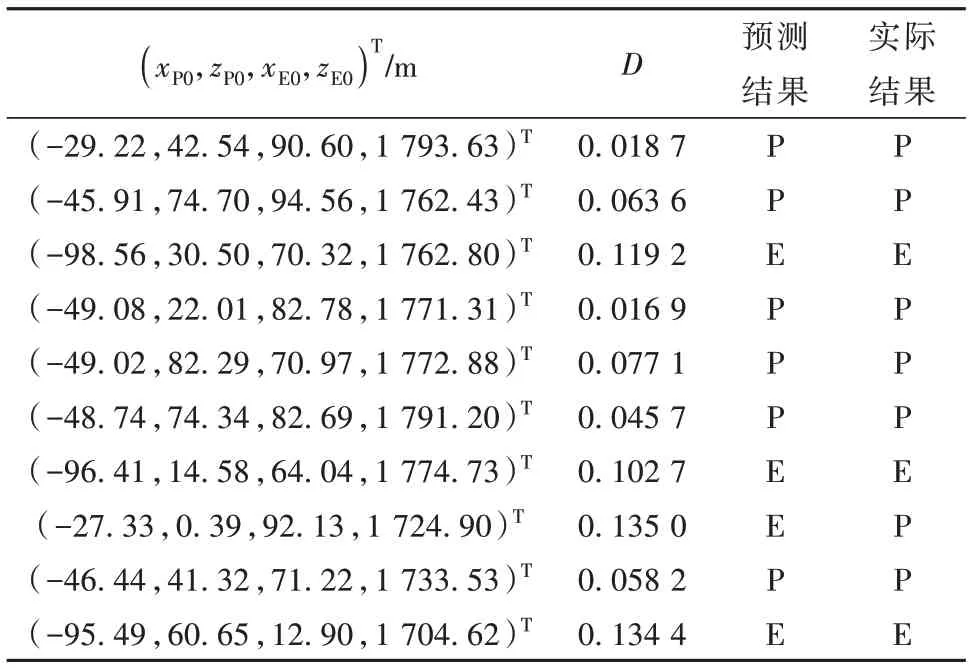
表6 采用孪生神经网络的捕获与逃逸预测Table 6 The predictions of the pursuit and escape success by using Siamese Network

由表6 可知，对比学习网络的区分正确率为95%，说明了此对比学习的孪生神经网络对于捕获域（逃逸域）表征的有效性。

4 结论

本文针对二维平面内无人机追逃博弈问题，研究了博弈均衡解的求取以及捕获域（逃逸域）的表征问题。主要结论有：提出了一种考虑零和博弈的无人机追逃博弈奖励函数设计方法，并建立了多智能体追逃博弈马尔科夫模型；构建了采用MADDPG算法的追逃博弈策略求解框架，并求得了博弈均衡解；提出了一种采用深度对比学习理论和孪生神经网络的捕获域（逃逸域）求解方法，实现了对2 个高维区域的有效区分和间接表征。