大质量比滚控式变质心飞行器动力学特性分析

孙佳慧，胡玉东，高长生，荆武兴

（哈尔滨工业大学航天学院，哈尔滨 150001）

0 引言

再入飞行器的常规姿态驱动采用气动舵控制［1-2］和喷气推力控制［3-4］两种方式。对于气动舵控制，在再入段高超声速飞行环境下存在舵面烧蚀问题［5-6］；而对于喷气推力控制，燃料作为额外负荷会降低再入飞行器的承载能力［7］。为弥补两种传统控制技术在再入飞行器应用方面的不足，近年来，变质心控制技术被提出。变质心控制通过移动安装在飞行器内部的质量块来改变系统质心的位置，气动力臂便随之改变，从而产生附加气动力矩来实现飞行器的姿态机动。相比于气动舵控制，变质心控制的执行机构安装在飞行器内部，从而保证了飞行器良好的气动外形，在减小飞行阻力的同时避免了舵面烧蚀问题；相比于喷气推力控制，变质心控制利用再入阶段所受气动力矩来改变姿态而无需消耗额外燃料。

1996 年，Petsopoulos等［8-9］首次将变质心控制应用于再入飞行器滚转控制中。该飞行器采用固定配平倾斜转弯（BTT）的机动方式，通过单活动体的运动来改变飞行器的滚转姿态。所设计的滚控式变质心再入飞行器在最大程度上减少了控制通道，并且避免了过于复杂的气动外形，为飞行器结构设计及控制系统设计带来便利，因此该构型一经提出，便受到广泛的关注与研究。文献［10］进一步讨论了该滚控式变质心再入飞行器的控制机理，并给出了3种提高飞行器机动能力的途径。文献［11］针对该构型存在的欠驱动控制问题设计了一种改进的欠驱动自抗扰控制器，该控制器充分利用了单个活动体的控制能力，提高了飞行器系统的抗干扰能力。近年来，为了提高飞行器的机动能力并优化飞行器内部空间，文献［12］提出了一种改进的大质量比滚控式变质心再入飞行器构型，并初步验证了该构型的有效性。然而，这一改进带来了两个亟需解决问题：首先由于活动体质量增加，其转动惯量不可忽略，文献［8-9］中将活动体视为质点的假设不再成立，需要单独建立活动体运动学模型。此外，固定配平BTT 控制模式下的滚转-偏航耦合问题在大质量活动体的影响下更加明显，这会增加飞行轨迹与预设轨迹的偏差，甚至产生不稳定的飞行状态。因此有必要进行系统动力学分析，以探究系统参数和偏航运动之间的关系，通过优化设计飞行器系统参数来减轻滚转机动对偏航运动造成的耦合影响。

传统变质心飞行器动力学分析将系统简化为线性模型并应用线性微分方程理论进行处理。例如，文献［13-14］将系统模型在平衡点处线性化，然而这一方法对于大质量比变质心飞行器这一强耦合、强非线性系统显然不再适用。在活动体运动的影响下，飞行器姿态响应存在多频振动现象，而不同的系统参数亦会引起状态响应的多值现象。故而有必要对活动体运动学与飞行器姿态动力学构成的非线性自治系统的解定量分析。多尺度法作为一种可以直观给出系统参数和运动规律之间关系的手段，被广泛应用于建筑工程［15-16］，材料科学［17-18］，电力工业［19-20］等领域。在飞行器性能及动力学行为分析领域，文献［21］研究了无人机大迎角飞行的纵向动力学，并通过多尺度法获得的近似解确定了影响稳定性的关键参数。文献［22］将马格努斯力矩假设为攻角的三次函数，并用多尺度法分别分析了对称和非对称再入飞行器的滚转运动响应。文献［23］通过飞行器俯仰姿态动力学方程揭示了多尺度法如何分离飞行器运动相关的各种特征时间。

本文建立了包含活动体偏转运动的完整飞行器姿态伺服动力学模型并对其进行非线性动力学分析，以此来优化飞行器的结构设计。

1 动力学模型

如图1 所示，本文的研究对象大质量比滚控式变质心再入飞行器主要由面对称载体B和内部大质量比活动体P组成，P的一端O1与载体铰接，另一端O2可在伺服机构作用下沿固定在xbO1zb平面的横向导轨移动。活动体的偏转会导致系统质心S偏移，在稳定的飞行条件下，载体的面对称气动外形会在纵对称面内产生固定配平攻角和作用在压心上的升力。由于气动力臂由S的位置决定，因此改变S的位置可控制滚转力矩，以实现飞行器的滚转机动。此外，由于缺乏俯仰姿态的控制输入，载体的非轴对称外形产生的固定配平攻角并不能被主动控制。为了描述变质心飞行器的动力学模型，定义惯性坐标系OXYZ，载体坐标系O1xbybzb和活动体固连坐标系O1xpypzp分别如图所示。其中O1xpypzp可由O1xbybzb绕二者公共轴线O1yb(yp)逆时针旋转δ角度得到，其中δ为活动体偏转角。因此从O1xbybzb到O1xpypzp的转换关系为：

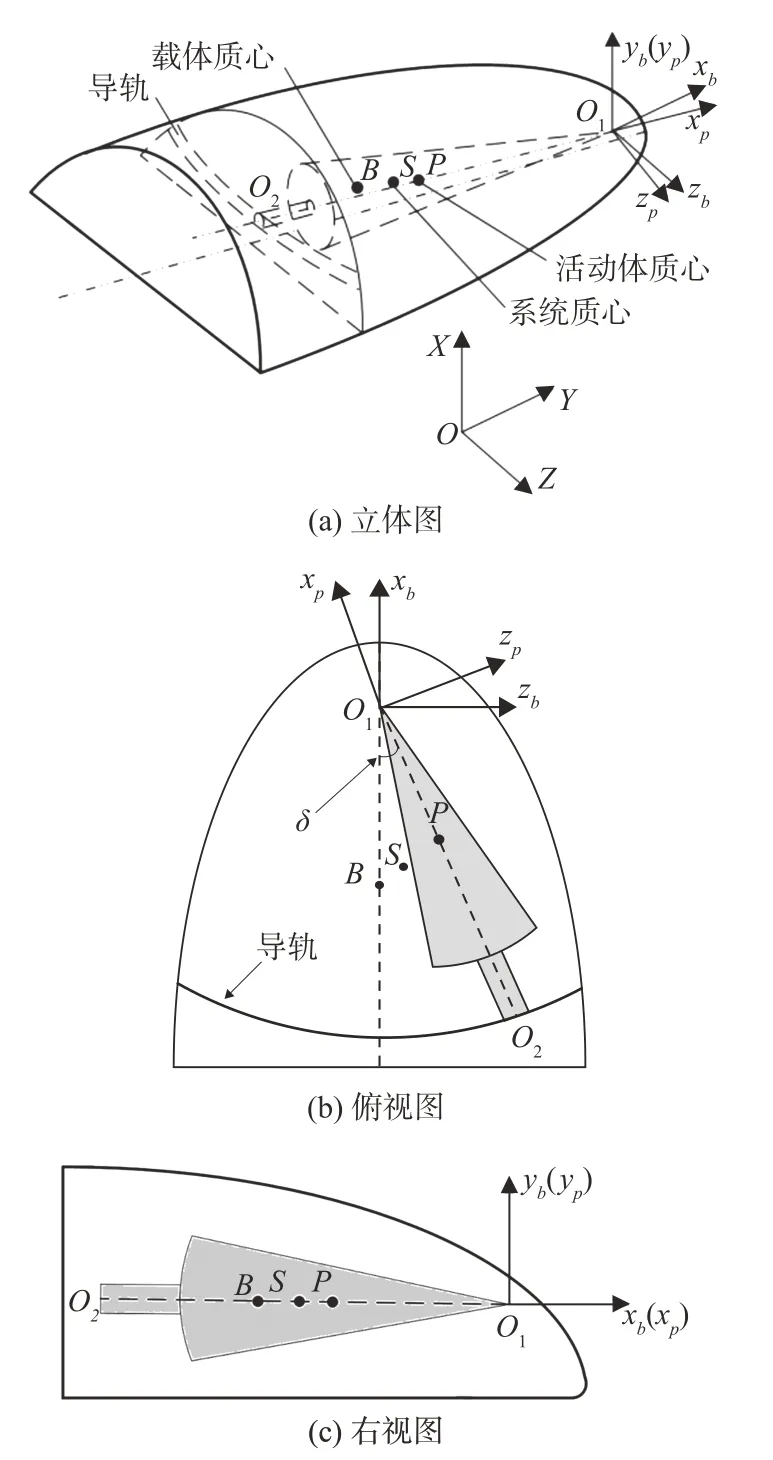
图1 大质量比变质心再入飞行器示意图Fig.1 Sketch of high-mass-ratio moving mass reentry vehicle

变质心飞行器动力学模型推导所涉及的符号定义如下：

1)mP和mB分别为活动体质量和载体质量，mS=mB+mP为系统总质量。活动体占系统的质量比为μP=mP/mS。

2) 载体坐标系下P和B相对O1点的位置分别为=[-LPcosδ0LPsinδ]T和=[-LB0 0]T，其中LP和LB分别表示P和B到O1的距离，活动体安装位置参数可表示为ΔBP=LP-LB。S相对O1点的位置为=+(1 -μP)。

3) 在载体坐标系下，载体的惯性角速度表示为ωB/I=[ωx ωy ωz]T，活动体相对载体的转动角速度表示为ωP/B=[00]T，活动体的惯性角速度为ωP/I=ωP/B+ωB/I。

4)IB=diag(IBx，IBy，IBz)表示载体坐标系下载体绕O1的惯性张量，IP=diag(IPx，IPy，IPz)表示活动体固连坐标系下活动体绕O1的惯性张量。

5)q=ρV2/2 为动压，其中ρ为大气密度，V为飞行器飞行速度大小。

6)S和L分别为飞行器特征面积和特征长度。

7)α，β和γ分别表示攻角，侧滑角和滚转角。

9) (⋅)′表示载体坐标系下的时间导数。

10) 矩阵a=[a1，a2，a3]T的叉乘算子表示为

1.1 系统动力学模型

根据动量定理，系统相对于质心S的动量矩惯性导数为：

式 中：rSP=MB和Faero分别为作用在系统压心上的气动力矩和气动力，分别在载体坐标系和速度系（x轴与飞行器速度矢量重合，y轴位于飞行器纵对称面内指向上，z轴与x，y轴构成右手直角坐标系）下表示为：

最后，将式（5）～（6）代入式（3）可得载体坐标系下系统姿态动力学方程：

式中：

从式（7）中可看出，对于大质量比变质心再入飞行器，活动体的惯性张量IP在载体坐标系下的投影JP不可忽略，这导致了和的增大，从而分别使得飞行器姿态间的耦合以及活动体偏转运动与飞行器姿态运动间的耦合增强。

1.2 活动体动力学模型

鉴于大质量比活动体的运动对系统动态特性影响显著，因此有必要建立活动体偏转的动力学模型。根据动量定理，活动体相对于质心P 的动量矩在惯性系下的导数可表示为

根据牛顿第二定律，活动体质心P和系统质心S的平动动力学为

式（7）和式（12）构成了大质量比滚控式变质心飞行器的完整姿态伺服动力学模型。从式（12）中可看出，由于活动体的转动惯量和质量不可忽略，其偏转运动使飞行器的滚转-偏航姿态耦合更加明显。由于滚转通道为主控姿态，但滚转-偏航耦合会导致在控制滚转机动的同时对偏航造成干扰，进而使飞行器飞行轨迹出现偏差。上述问题对飞行器的构型设计提出要求，即如何优化设计变质心飞行器的构型参数来降低控制输入对飞行器偏航通道的影响。

2 飞行器姿态动力学分析

对于固定配平BTT 控制模式，欠驱动俯仰通道的稳定性是获得有效滚转控制的前提，而对于所提出的滚控式大质量比变质心再入飞行器，讨论俯仰稳定性与活动体配置参数之间的关系具有重要意义。此外，从上一节的完整姿态伺服动力学模型简要分析中可看出，大质量活动体势必会加剧飞行器滚转-偏航姿态耦合及活动体偏转运动与飞行器姿态运动之间的耦合。因此，本节首先分析了所提出的滚控式大质量比变质心飞行器的纵向静态稳定性和耦合特性。

为了定量分析，作如下假设：

1) 纵向静稳定性分析中，侧滑角β在原点处稳定，侧滑角速度ωy可忽略；

2) 活动体偏转角δ为小量（cosδ≈1，sinδ≈δ），其高阶项可忽略。

2.1 纵向静稳定性分析

本节考察活动体配置参数，即质量比μP和安装位置ΔBP=LP-LB对飞行器纵向静稳定性和固定配平攻角的影响，据此来设计活动体的配置参数。

根据假设1），攻角α的导数可简化为：

俯仰姿态动力学可简化为：

式 中：Ix=JPx+(1 -μP)mPLPδ(LP-LB)，Iz=IBz+JPz+(1 -μP)mP(LB-LP)2。

联立式（12）～（13）可得攻角的微分方程：

式中：

由式（15）知，A1，A2和B0取决于飞行器的气动参数、构型参数和速度，B表示由不可忽略的附加相对转动惯量引起的俯仰通道和滚转通道耦合项。

根据Routh 准则构造Routh 判据，可以得到系统的纵向静态稳定条件为A1>0，A2>0。根据>0，Cx>0,<0，可知A1>0 成立。A2>0 可由以下不等式给出：

给定气动参数Cx=0.110 7，=0.1，=-0.005 5，=-2.682，飞行器参数S=1.5 m2，L=5.3 m，V=3 400 m/s，飞行器纵向静态稳定性区域由图2 给出。由图可知在纵向静稳定区域内，不同活动体质量比μP给定，其安装位置参数ΔBP将会受到限制。因此，为了保证俯仰姿态稳定，应合理地选择活动体质量比及其安装位置。图3给出了在滚转稳定和零初始条件下，依据图2 选择不同活动体配置参数的攻角动态响应，从中可以看出，攻角在气动配平力矩下快速收敛。

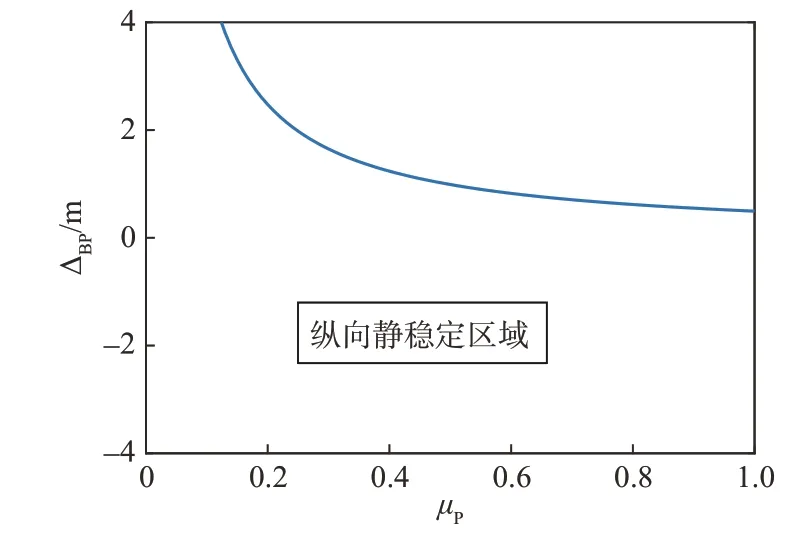
图2 纵向静稳定区域Fig.2 Longitudinal static stable region

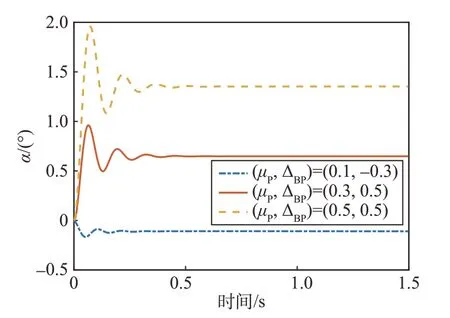
图3 静稳定参数下攻角响应Fig.3 Angle of attack under static stability parameters

显然，配平攻角随活动体配置参数μP和ΔBP而变化，因为这些参数影响决定气动力臂的系统质心位置，进而产生不同的气动配平力矩和不同的配平攻角。因此，变质心再入飞行器的构型参数不仅要保证纵向静态稳定性，还要根据给定飞行条件下的预期配平攻角进行选择。

2.2 姿态耦合分析

本节将对大质量比滚控式变质心飞行器姿态耦合及活动体偏转运动对飞行器姿态运动的耦合影响进行初步定量分析。由式（7）可知，飞行器姿态角加速度和滑块偏转角加速度通过惯量矩阵和耦合，这种耦合关系可以通过改写式（7）表示如下：

显然Φ=[f1f2f3]反映了飞行器姿态角加速度与滑块偏转角加速度之间的耦合关系。由于=[00]T，为了测量这一关系，定义耦合指数σ(δ)=‖‖f22，其与活动体的质量比μP和活动体偏转角δ密切相关。图4为不同μP下耦合指数随δ变化曲线。从图中可以看出，耦合随活动体质量比的增加而增大，当μP=0.24 时，耦合指数曲线近似为直线，耦合不受活动体位置的影响；当μP<0.24时，曲线为凹形，此时δ接近0 时耦合减至最小；当μP>0.24时，曲线为凸形，此时δ接近0时耦合最大。

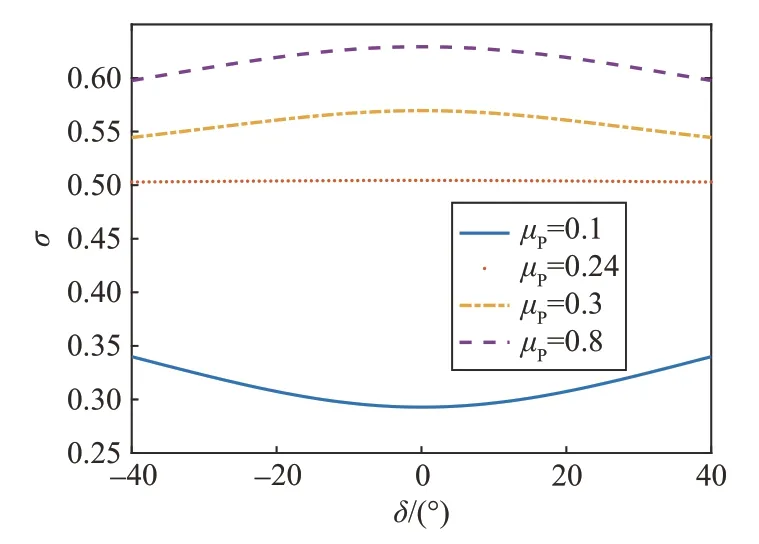
图4 耦合指数曲线Fig.4 Coupling index curve

式（20）从系统整体姿态动力学的角度分析了活动体偏转与飞行器姿态间的耦合程度，为了充分考虑飞行器各姿态间的耦合，将式（7）改写为滚转、偏航、俯仰3通道姿态动力学形式：

从式（23）可以看出俯仰姿态动力学只有由惯性张量Izx和Ixy引起的角速度耦合项，并不受活动体偏转的影响，可由第2.1节的分析保证其稳定性。然而根据式（21）～（22），除角速度耦合项外，滚转通道的控制输入δ也作用于偏航通道，说明在活动体偏转进行滚转机动时，偏航通道将不可避免地产生耦合效应。给定气动参数Cx=0.110 7，=-0.005 5，=0.1，=-2.682；飞行器参数V=3 400 m/s，S=1.5 m2，L=5.3 m，IB=diag(100，500，500) kg·m2；活动体构型参数IP=diag(30，200，200) kg·m2，μP=0.3，ΔBP=0.5 m。图5 给出了当偏航通道受到影响而产生β0=3°的初始偏差后若停止姿态机动，即无控制输入下系统俯仰、偏航、滚转通道的开环响应。由图可知，在无控状态下（δ===0），系统俯仰通道可在气动阻尼力矩下快速达到平衡，偏航通道虽最终稳定在平衡点附近，但依然做小幅震荡。

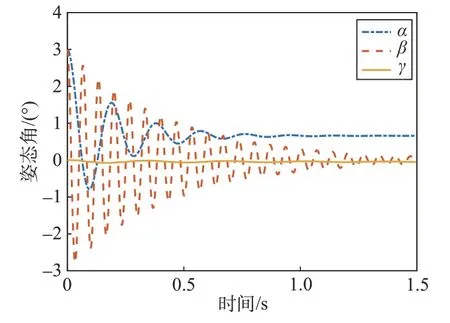
图5 俯仰、偏航、滚转姿态的开环响应Fig.5 Open loop response of pitch，yaw，and roll attitudes

图6给出了零初始攻角和侧滑角在非零活动体偏转角下的响应。如图6（a）所示，活动体连续偏转3°时，攻角和侧滑角首先做减幅振荡。尽管攻角和侧滑角依赖于纵向静稳定性和航向静稳定性在一段时间后趋于稳定，但如果飞行环境需要频繁的活动体偏转，将不可避免地导致耦合系统不稳定。在图6（b）所示的偏转角为7°情况下，侧滑角受到活动体连续偏转的严重影响而快速振荡，同时导致攻角的发散。因此，在前述给定的飞行器及活动体设计参数下，当活动体发生较大的频繁偏转或侧滑角产生较大初始偏差时，侧滑稳定性的假设就不再成立。那么，如何设计大质量比滚控式变质心飞行器的构型参数来使得活动体偏转实现滚转姿态控制时对偏航姿态耦合尽可能小，便能在飞行器结构的优化设计上提高飞行器的可控性能，降低控制器设计的难度。

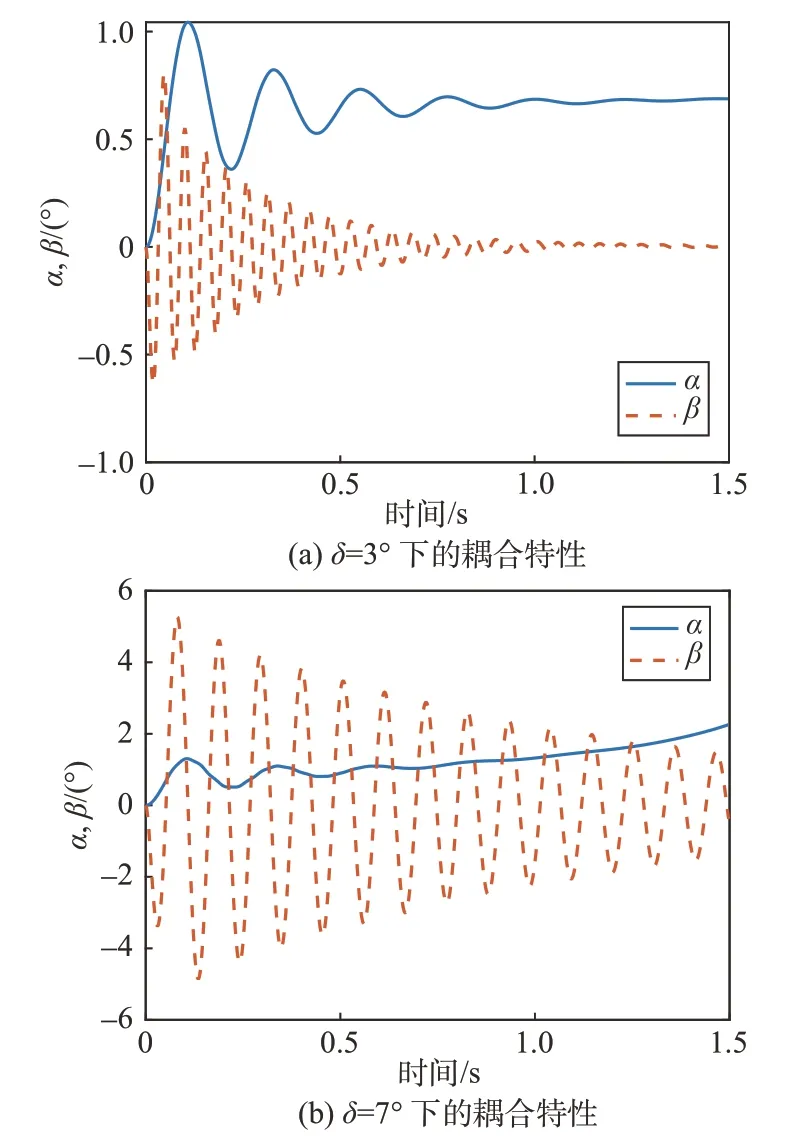
图6 不同δ下的俯仰偏航姿态响应Fig.6 Pitch and yaw attitude response under different δ

3 活动体偏转与偏航姿态耦合振动分析

由前述飞行器姿态耦合分析可知，活动体偏转控制滚转姿态的同时会对偏航通道产生耦合影响。对于偏航姿态动力学和活动体偏转动力学构成的非线性多自由度系统，自由度间的耦合振动不可避免，而该耦合振动会对飞行器的稳定飞行造成不利影响。此外，驱动活动体的伺服力作为耦合系统的外激励，其不同频率可造成耦合系统状态的不同稳态振动。针对上述问题，本文采用多尺度法对活动体偏转角和飞行器侧滑角可能出现的共振情形进一步分析。对于不同外激励频率产生的内共振定常解，探究其幅频特性和系统参数间的关系，以通过设计飞行器构型参数和活动体配置参数来减轻系统耦合振动，进一步优化系统动力学特性。

由式（7）与（12）可得包含活动体偏转动力学的非线性偏航通道动力学：

式 中：Iy2=Iδ1=JPy+mP(1 -μP)LP(LP-LB)，Iδ2=JPy+mP(1 -μP)；F为驱动活动体的伺服力大小；为活动体长度。

侧滑角的变化规律为：

由式（28）知，在伺服力F的激励下，活动体偏转与飞行器偏航姿态耦合系统是立方非线性二自由度受迫系统。系统自然频率可通过求解刚度矩阵的特征值得到：

为探究该非线性动力学响应，采用多尺度法进行摄动分析。在多尺度框架下，将外激励表示成简谐激励形式F=fcos(ωt+φ)，并引入小参数ε，则式（28）可改写为：

式中：Mj=，j=1，2。

设式（31）的解的形式为

式中：T0=t和T2=ε2t分别为多尺度框架下的快时间尺度和慢时间尺度。

将式（32）代入式（31）并引入导算子∂/∂Tj=Dj，j=0，2。按ε与ε3合并同类项，可得：

方程（32）的解可表示为如下复数形式：

式中：ηj=ρ2/(-k2)，j=1，2；fcc代表前面所有项的复共轭。

将式（35）代入式（34）有：

由式（36）知，当变质心飞行器参数和飞行参数使得系统自然频率满足ω1=3ω2时会发生1∶3 内共振，此时作用在活动体偏转模态的外激励会通过能量转化作用到飞行器偏航姿态上。而外激励F的频率与系统自然频率相同时，则又会产生主共振。当ω1≈3ω2时，引入调谐参数σ1：

由系统自然频率可知主共振产生有ω≈ω1和ω≈ω2两种情况，接下来将分别讨论不同主共振情况下系统的一阶近似定常解。

3.1 ω ≈ω1的系统一阶近似定常解

当驱动活动体的外激励频率ω≈ω1时，引入调谐参数σ2：

为消除长期项，设式（36）的特解为：

将式（38）～（39）代入式（36），比较等式两端ω1和ω2的系数，有：

根据式（40）的可解性条件有：

将式（41）代入式（42）得到消除长期项条件：

令Λj=，j=1，2。代入式（43）后分离实部和虚部，则系统一阶近似解的振幅和相位满足：

式中：(⋅)′表示对T2求导；ψ1=3θ2-θ1-σ1T2，ψ2=σ2T2-θ1+φ。

3.2 ω ≈ω2的系统一阶近似定常解

当驱动活动体的外激励频率ω≈ω2时，同样引入调谐参数σ2：

按照与式（36）～（43）相似的步骤求解得到系统一阶近似解的振幅和相位满足：

由式（46）及式（49）可知，飞行器参数、活动体配置参数以及驱动活动体的伺服力均可影响系统的幅频响应，故合理设计变质心飞行器的构型参数对于降低飞行器非线性耦合程度，提高飞行器控制性能尤为重要。

3.3 数值仿真

下面将对式（46）及式（49）表示的系统一阶近似解的稳态幅频特性进行仿真分析。仿真气动参数为Cx=0.110 7，=-2.682，=-0.005 5，=0.1，飞行器参数为V=3 400 m/s，S=1.5 m2，L=5.3 m，IB=diag(100，500，500) kg·m2。根据以上参数求得系统自然频率为ω1≈34.90 rad/s，ω2≈12.42 rad/s。

1)ω≈ω1的主共振

外激励频率接近系统第一自然频率时，图7 给出了不同μP下系统的幅频响应曲线，其中实线代表稳定响应，虚线代表不稳定响应。在非线性影响下，幅频响应曲线向右弯曲并形成多值性，且随着μP的增加右弯明显，最大振幅对应频率更加偏离ω1。

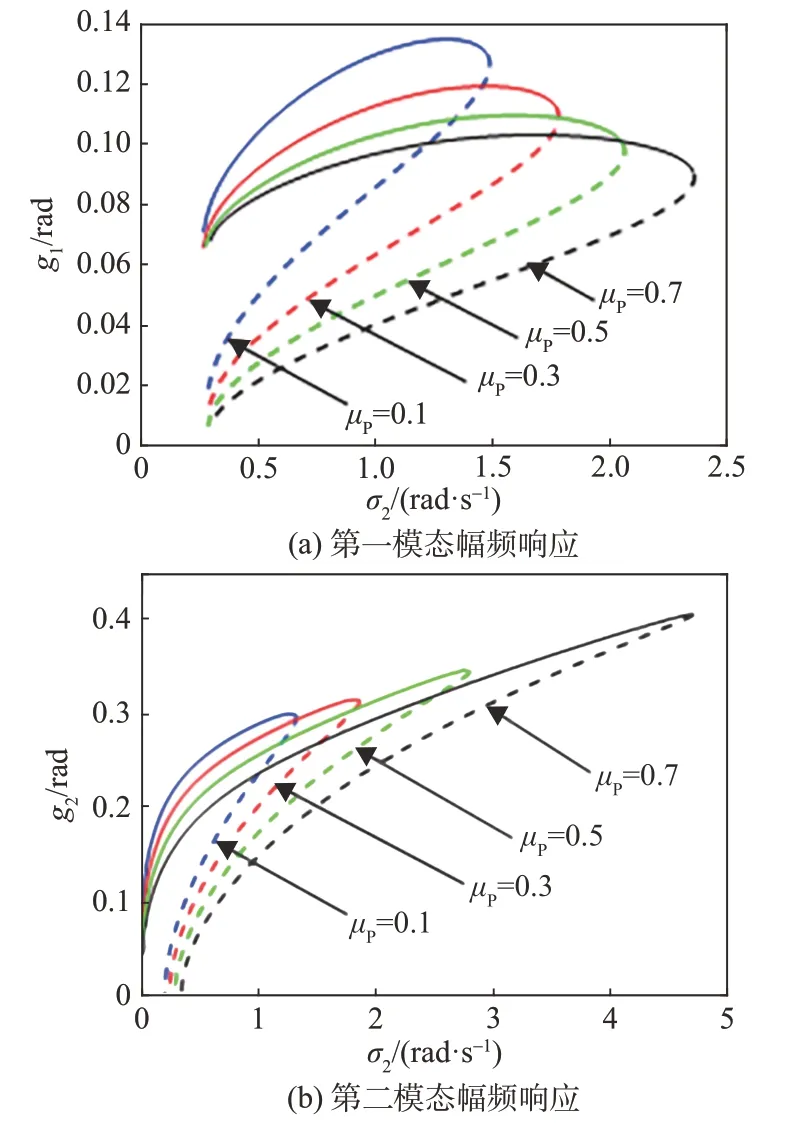
图7 ω ≈ω1时不同质量比下的幅频响应Fig.7 Amplitude frequency response versus different mass ratios under ω ≈ω1

图8 给出了不同活动体安装位置ΔBP对系统幅频响应曲线的影响。根据ΔBP的定义可知ΔBP越大，活动体安装越靠后。与不同活动体质量比对系统幅频响应的影响类似，由图可知幅频响应曲线随活动体安装位置的后移而向右弯曲，且活动体安装位置越靠后，最大振幅越大，其对应频率更加偏离ω1。

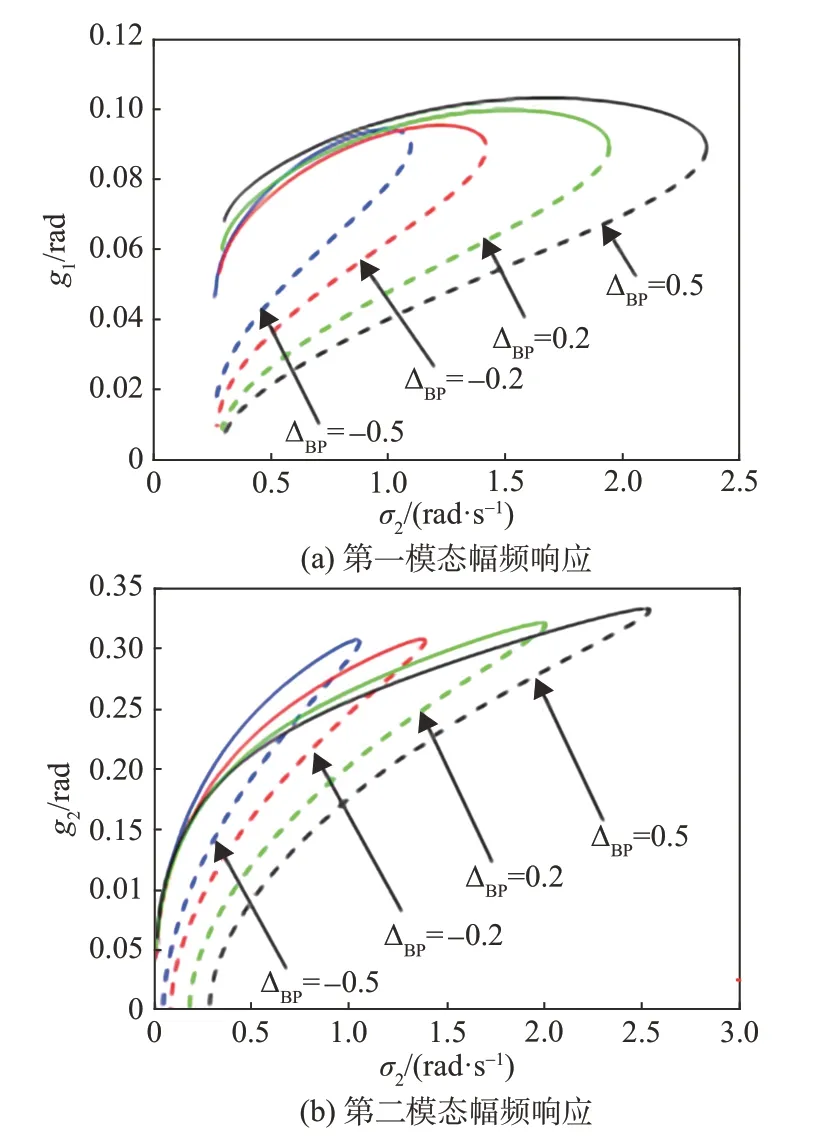
图8 ω ≈ω1时不同安装位置的幅频响应Fig.8 Amplitude frequency response versus different installation positions under ω ≈ω1

2)ω≈ω2的主共振

当ω≈ω2时，类似地，首先给出不同活动体质量比μP下系统幅频响应曲线，如图9 所示。由图可知，系统幅频响应曲线峰值对应的频率随μP增加而右移，且随着μP增大，响应幅值增加明显。为了降低系统的耦合振动，活动体质量不宜过大。但这与增大活动体质量以增强变质心飞行器机动性和控制能力相矛盾。故活动体质量比应结合飞行器的机动能力需求和耦合共振约束来折衷选取。

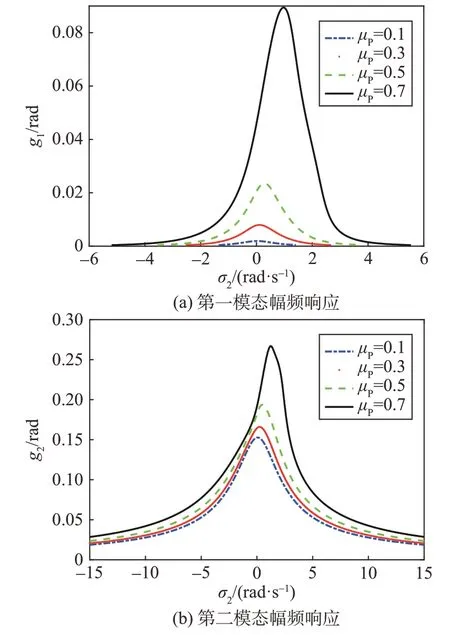
图9 ω ≈ω2时不同质量比下的幅频响应Fig.9 Amplitude frequency response versus different mass ratios under ω ≈ω2

图10给出了活动体不同安装位置ΔBP对系统幅频特性的影响曲线。由图可知，活动体安装越靠前，即ΔBP越小，系统耦合共振幅值越小。故为了减轻活动体偏转对偏航通道的影响，活动体安装位置不宜太靠后。但活动体安装越靠前，配平攻角也越小，这会造成变质心飞行器所受升力减小。而根据滚控式变质心飞行器的控制机理，活动体偏转产生的滚转控制力矩主要由升力提供，这会造成变质心飞行器的控制性能降低。故而活动体安装位置设计需综合考虑飞行器控制性能需求和耦合共振约束。

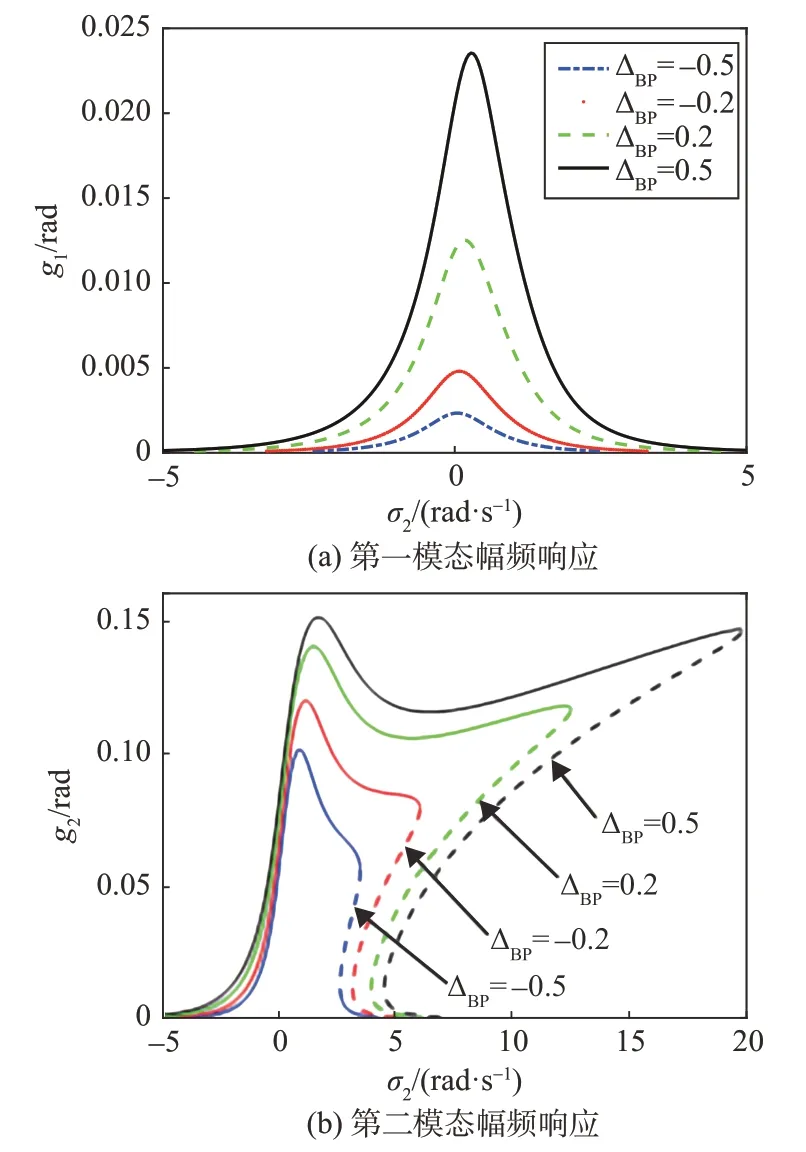
图10 ω ≈ω2时不同安装位置的幅频响应Fig.10 Amplitude frequency response versus different installation positions under ω ≈ω2

4 结论

本文针对大质量比滚控式变质心再入飞行器，建立了包含活动体偏转运动的完整飞行器姿态伺服动力学模型，并探讨了大质量比变质心飞行器与小滑块变质心飞行器相比在动力学上具有更强的非线性和耦合特性的原因。为了减少大质量比变质心飞行器姿态动力学中的耦合效应，避免飞行器出现不稳定的飞行情况，采用多尺度法获得了不同构型参数下活动体偏转和偏航姿态耦合系统的近似解析解，进而提出了考虑滚转-偏航耦合约束的飞行器构型设计方案，以减少对偏航通道的干扰，提高系统性能，并最终通过数值仿真验证了方案的有效性。研究结果揭示了系统耦合特性的机理和变化规律，为面向性能的飞行器构型设计提供了理论依据。