面向天文多普勒差分测速的太阳/行星光谱对生成方法

刘劲，徐玉豪，尤伟，陈晓，张子军，马辛

（1.武汉科技大学信息科学与工程学院，武汉 430081；2.北京航空航天大学仪器科学与光电工程学院，北京 100191；3.上海卫星工程研究所，上海 201109）

0 引言

进入21世纪，航天大国纷纷开启各自的深空探测计划。中国航天筑梦苍穹：“嫦娥”奔月［1］、“祝融”探火［2］、“羲和”追日［3］，这些航天任务的成功实施标志着中国的深空探测技术日趋成熟。导航作为未来深空探测计划必不可少的关键技术，需满足的要求日趋增高。尤其是在行星探测的捕获阶段，航天器与地面站之间的通信延迟长，而捕获期短，地面站无法为航天器提供实时高精度的导航信息。天文导航不依赖地面站，成为解决这一问题的关键技术。

天文导航有测角、测距、测速3种方式。测角导航和测距导航分别以航天器与近天体夹角［4］、脉冲星到达时间［5］作为测量量，通过卡尔曼滤波，间接获得航天器速度。为了直接获得速度信息，测速导航应运而生，它根据多普勒效应，测量天文光谱频移，获得速度信息，弥补了测角与测距导航的不足。通常情况下，测速会与测角或测距相结合［6-8］，以提高组合导航的精度。上海卫星工程研究所和中国科学院研制的太阳原子鉴频器［9］已完成在轨验证，证实了天文组合导航的可行性与精确性［10］。天文多普勒差分导航［11］通过差分技术消除了太阳活动的影响，成为研究热点。其测量量是太阳光谱频移和行星光谱频移之差。

目前，针对天文光谱频移估计方法的研究进行得如火如荼，且已取得了一系列研究成果。欧洲南方天文台（ESO）的高精度径向速度行星搜索器（High accuracy radial velocity planet searcher，HARPS）利用互相关函数算法估计径向速度［12］。模板增强径向速度再分析应用算法比互相关函数算法具有更高的精度［13］。基于最小二乘匹配的光谱径向速度分析仪的径向测速精度［14］可达1 ms-1，用其对HARPS 径向速度数据库的系统误差进行校正［15］。Silva等［16］提出了一种基于模板匹配的半贝叶斯方法。Rajpaul等［17-18］提出了无需高信噪比模板，仅用高斯过程对光谱建模测速的方法。文献［19］通过建立偏移和补偿模型降低太阳自转引起的多普勒偏差给测速造成的影响。文献［20］提出针对边界效应的天文光谱测速方法，解决天文光谱测速中的非线性傅立叶相移问题，使天文测速精度进一步提升。以上方法均是观测同一个天体，其光谱并不会受行星反射，自转等影响。天文差分测速则是利用太阳和行星光谱对比，行星光谱必然受到多种因素干扰。因此，不能照搬传统天文测速方法，而是要根据天文差分测速的特点，研究新的信号处理方法。

太阳是一个宏观稳定，但微观极不稳定的星体。由太阳耀斑等引起的太阳光谱扰动［21-22］、光谱线深度的差异以及行星反射率都会对多普勒差分测速造成影响［23］。通过建立速度误差模型［24］，对太阳多普勒差分导航中直接和反射太阳光源的面积重叠率、时间色散以及太阳自转多普勒误差3 个几何误差源进行分析［25］。多普勒差分测速原理上要求测速光谱产生于同一时刻离开太阳的太阳光子［26］。但目前缺乏时间同步的太阳直射和行星反射实测光谱数据。

在图像生成方面，学者们先后提出变分自编码器（VAE）和生成对抗网络（GAN）。GAN 自2014 年被提出至今，在图像处理、机器视觉等领域被广泛引用，并改进出多个变体，如Wasserstein 生成对抗网络［30-31］、条件对抗生成网络［32］以及双判别器对抗生成网络［33］。按照配对原则可将GAN 分为非配对网络和配对网络，如循环生成对抗网络［34］（Cycle GAN）和对偶生成对抗网络［35-36］（Dual GAN）。由于行星和太阳光谱的轮廓大致相同，仅存在由宇宙中的各种影响因子引起的细节上的不同，符合Dual GAN 的主体不变、细节转换的特点，所以此次实验选用Dual GAN。同时Dual GAN 继承了Wasserstein生成对抗网络损失函数不会梯度消失的优点，这也是选择Dual GAN的主要原因。

为了解决同步光谱对缺失的问题，本文利用Dual GAN 将非同步的太阳/行星光谱对转换为同步的太阳/行星光谱对，用于多普勒差分测速。针对训练集有限，进而导致泛化性差这一问题，本文把Dual GAN 与VAE 结合起来，利用VAE 的数据增强能力增广训练集。解码器与生成器的作用相似，同为生成过程。因此，用Dual GAN 的生成器取代VAE 中的解码器，使VAE 和Dual GAN 融合为VAE-Dual GAN。同时，利用Dual GAN 网络的重建损失约束作用同时训练生成器、判别器和VAE 的编码器。

1 VAE-Dual GAN

为了生成同步的太阳/行星光谱对，考虑到VAE的数据增广能力，本文将VAE 和Dual GAN 结合起来，提出了VAE-Dual GAN，介绍了其网络结构，并从理论上分析了子网络的泛化性。

1.1 网络模型结构

VAE-Dual GAN 结构如图1 所示，模型由编码器、生成器和判别器各2 个组成。生成器重构损失和编码器重构损失分别用虚线和点划线表示。黑色虚线框内为VAE-生成器模块。黄色和蓝色的实线箭头分别表示伪太阳光谱和伪行星光谱生成过程。在伪行星光谱生成过程中，首先，编码器Φsun将真实太阳光谱Ssun映射到太阳光谱隐空间Zsun，并在Zsun内采样得到太阳光谱样本zsun。然后，生成器将zsun转化为与之同步的伪行星光谱。最后，伪行星光谱经过对偶编码器Φplanet和对偶生成器Ψplanetsun生成重构太阳光谱。伪太阳光谱生成过程与之类似。Splanet表示真实行星光谱；和分别表示伪太阳光谱和重构行星光谱；Zplanet和分别代表真实行星光谱和伪太阳光谱经过编码器后的隐空间。

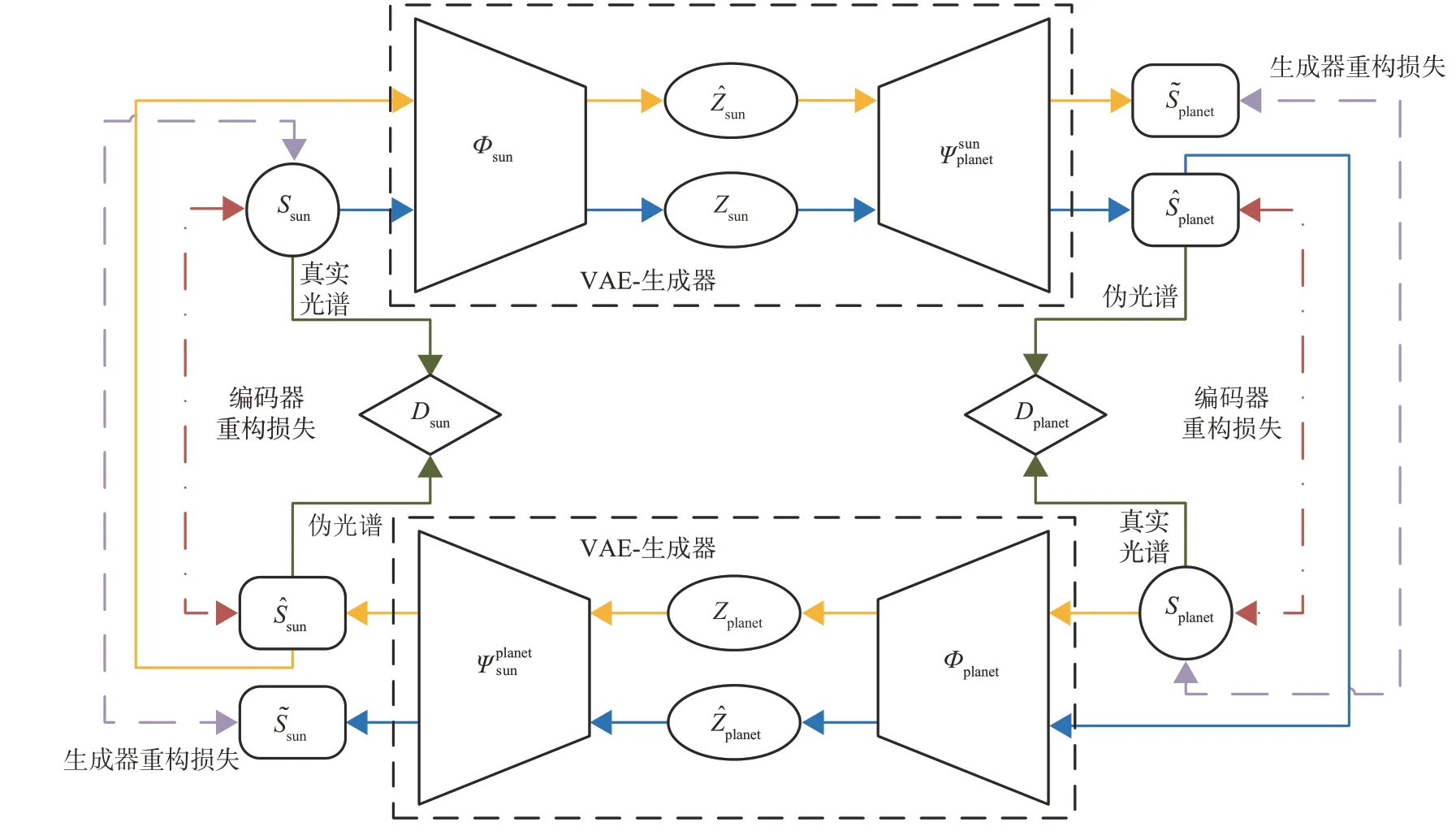
图1 VAE-Dual GAN结构图Fig.1 VAE-Dual GAN structure

图1 中黑色虚线框中的VAE-生成器模块结构如图2所示。该模块利用生成器与VAE网络中的解码器作用相似的原理，用Dual GAN 的生成器代替VAE 解码器，构成VAE-生成器模块。Ssun域中的太阳光谱样本为ssun，隐藏层Hj上方的数字代表神经元数，隐藏层之间的FC 代表全连接，编码器通过采样输出均值μ(i)和方差σ2(i)，编码后的隐空间样本zsun服从正态分布N(μ(i)，σ2(i))，然后通过生成器模块生成Splanet域的伪行星光谱。

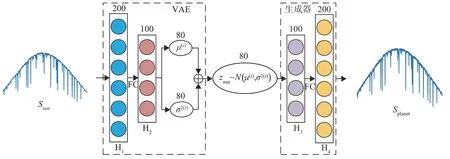
图2 VAE-生成器结构图Fig.2 VAE-generator structure

VAE 损失函数由KL 损失LKL和编码器重构损失构成，其表达式为：

式中：μ1和μ2分别为太阳和行星经过编码器输出的均值；和分别为二者的方差；α∈(0，1)为控制KL散度的约束能力的常数。

判别器损失Ld表达式为：

生成器损失Lg表达式为：

式（1）～（4）构成VAE-Dual GAN 网络的总损失Ltotal，表达式为：

式中：β∈[0，1]为作用于生成器重构损失的常数，用来均衡生成器重构损失对网络的作用力，防止其造成的过拟合现象。

1.2 泛化性分析

VAE-Dual GAN 由2 个互为对偶的子网络模型构成，两个VAE 的作用是增广训练集。因此只需证明Dual GAN 其中一个网络的泛化性即可。要证明泛化性，首先需要Lipschitz连续定义。

定义1.对于任意2 个样本x和y，如果损失函L(x)相对于距离度量Δ满足：

则称L(x) 是Lipschitz 连续。其中，κL是Lipschitz常数。

在Dual GAN的子网络中，分布之间的Wasserstein距离表达式为：

式中：f≤1 为连续函数，f满足1-Lipschitz 连续；x和y分别为服从X和Y分布的样本。

根据定义1，引入判别器函数fω和生成器函数gθ后，由式（7）可以得到目标函数为：

式（8）用来衡量判别器对真实样本和生成样本的区分质量。如果泛化效果好，随着样本数量的不断增加，无限分布与有限分布之间的差异会更小。

利用给定的h个样本Xh={x1，x2，…，xh}和Yh={y1，y2，…，yh}，分别服从分布和（分别是分布X和Y的有限分布），在固定生成器的情况下，式（8）可以重写为：

本文定义无限分布下和有限分布下的目标函数U和Uh为：

如果网络泛化成功，在输入样本增加到一定的数量后，两式的差值|Uh-U|会依概率收敛为0；如果泛化失败，它将不能依概率收敛为0，这也意味着生成的分布过拟合真实分布。

文献［37］受GAN 及其变体用有限的样本最小化真实分布X和生成分布Y的散度或距离的启发，对GAN的泛化性定义如下：

定义2.对于生成分布Y，如果分布之间的距离或散度d(⋅，⋅)用含有h个训练样本的有限分布和进行泛化，大概率式（6）成立，即：

则称GAN具有泛化性。

根据定义1和定义2可以证明以下定理。

定理1.在与有界Lipschitz 常数κL有关的假设条件下［38］：

I.fω(x)在参数ω上是Lipschitz 连续，即对任意ω都有|fω(x) -fω′(x)|≤κL‖ω-ω′‖；

II.fω(x)在样本x上是1-Lipschitz 连续，即对任意x都有|fω(x) -fω(x′)|≤κ‖x-x′‖；

III.两个样本的距离存在边界BΔ，即|Δ(x，x′) |≤BΔ。

式中：a为目标函数的参数数量。

证.将式（10）～（11）代入式（13）得式（14）：

需要说明：

由McDiarmid’s不等式可以得到：

（1）在网络N 内将式（15）表述的变化边界从适用于单个判别器函数fω推广为联合边界，即对于网络N 中的判别器函数fω，总存在一个ω′∈N 有‖ω-ω′‖≤这个网络中所包含的损失函数满足|N|≤其中a表示损失函数中的参数数量。

（2）分析在网络N 之外的 判别器函数fω的情况。

因此，可以得出包括所有损失函数的联合边界：

定理1 得证。这表明了VAE-Dual GAN 有一定的泛化性。

2 天体光谱测速

多普勒效应是由于波源与观测点的相对运动，使观测光谱波长与原波长存在频移。在只考虑多普勒效应下，航天器观测到的行星光谱波长λp与太阳光谱波长λs的关系如下：

式中：c为光速；v为径向速度。

对式（24）取对数，可以得到对数波长偏移τ为：

设太阳光谱ssun(lnλn)和行星光谱splanet(lnλn)的关系表达式为：

式中：ο(lnλn)为未知的反射率函数；λn为离散波长。

由于光谱的波长间隔不均匀，而原离散傅立叶变换无法处理非均匀间隔波长的光谱，所以采用非均匀离散傅立叶变换（NDFT）方法，表达式为：

式中：Lλ=lnλmax-lnλmin为对数波长的长度；k=1，2，…，K。

式（27）经过NDFT后，splanet(lnλn)和ssun(lnλn)的幅值Splanet(k)与Ssun(k)的累积误差为：

式中：ςk为傅立叶频率下噪声振幅的平方根；ϑ(k)和φ(k)分别为splanet(lnλn)和ssun(lnλn)的相位；Ο(k)和ϖ(k)分别为ο(lnλn)经过NDFT的幅值和相位；⊗为循环卷积符号。

当太阳/行星光谱对同步时，行星光谱仅受反射率影响；当太阳/行星光谱对不同步时，除反射率外，行星光谱还受太阳活动、太阳自转等因素影响，ο(lnλn)的表达式复杂。因此，同步的太阳/行星光谱对可有效减小干扰因素的影响，提高测速精度。

3 实验结果与分析

3.1 实验参数

初始学习率设为0.000 1，并且每100 次迭代衰减1.5%。隐藏层使用Leaky ReLUs 作为激活函数，泄露值设为0.2。网络优化器为RMSProp（Root mean square prop），并将每次更新的判别器梯度的绝对值修正到不超过截断常数，其值为0.1，优化器衰减速率为0.9。实验平台为宏碁笔记本，其处理器主频为3.10 GHz，内存为16 GB。

3.2 数据集

本文数据集为ESO的HARPS观测的天文光谱，该仪器覆盖的光谱波长范围为380～690 nm，仪器的探测器由2 个电荷耦合器件（CCD）组成，每个CCD分别可以读取到36个波长区间的光谱，共72段光谱。相较于第2 个CCD，第1 个CCD 读取到的光谱的信噪比较低。在第2 个CCD 的35 个波长区间的光谱中选择光谱进行测速。

实验太阳和月球光谱的4 个波长范围，包括：5 964.872-6 032.103Å；6 337.527-6 408.976Å；6 541.882-6 615.640Å；6 685.603-6 760.982Å。它们各有特点：5 964.872-6 032.103Å 区间信噪比高而RV标准差低；6 337.527-6 408.976Å区间信噪比高且RV 标准差高；6 541.882-6 615.640Å 区间是CHASE 工程的模板光谱；6 685.603-6 760.982Å区间是随机选择的，其信噪比高而RV 标准差介于5 964.872-6 032.103Å 与6 337.527-6 408.976Å之间。

3.3 光谱测速与相似度

为了验证VAE-Dual GAN的可行性，将3种天文光谱的测速结果进行对比，如表1所示。3种天文光谱包括：生成的伪月球光谱，加高斯噪声的月球光谱，加泊松噪声的月球光谱。本文用Evr表示真实月球光谱径向速度标准差；Evp和Evg分别表示引入泊松噪声和高斯噪声的光谱测速标准差。

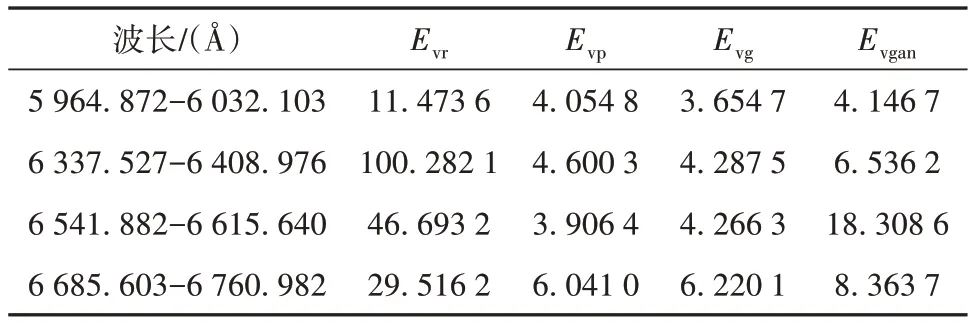
表1 径向速度标准差Table 1 Standard deviation of radial velocity

表1显示，VAE-Dual GAN 生成的伪月球光谱径向速度标准差Evgan低于Evr，高于Evp和Evg，表明噪声不是影响光谱测速精度的唯一因素。生成的同步光谱测速精度高于非同步光谱测速精度。

为了说明真实太阳光谱和生成的伪月球光谱的时间同步性，本文引入了结构相似指标度量［39］（Structure similarity index measure，SSIM）。结构相似指标用来衡量两幅图像的相似度，计算公式为：

式中：μsun和μplanet分别为太阳光谱和行星光谱的均值和分别为二者的方差；σsun_planet为太阳光谱与行星光谱的协方差。VSSIM的取值范围为[0，1]。VSSIM越大，表示二者相似度越高。表2给出了4种天文光谱对的VSSIM值，包括：真实太阳/真实月球光谱对（Real sun/Real moon，Rs/Rm）、真实太阳/伪月球光谱对（Real sun/Fake moon，Rs/Fm）、真实太阳/泊松噪声月球光谱对（Real sun/Poisson noise moon，Rs/Pm）、真实太阳/高斯噪声月球光谱对（Real sun/Gaussian noise moon，Rs/Gm）。

表2 结构相似性（SSIM）Table 2 Structural similarity index measure（SSIM）

表2 可以看出，对于每个波长区间，Rs/Rm 的SSIM 低于Rs/Fm，高于Rs/Pm 和Rs/Gm。这说明伪月球光谱与真实太阳光谱的SSIM 高于真实月球光谱与真实太阳光谱的SSIM。太阳表面活动引起了光谱的变化。时间不同步造成真实月球光谱与真实太阳光谱的SSIM 低。Rs/Fm 的SSIM 高，这说明二者的时间是同步的。此外，引入噪声会降低光谱对的SSIM。这表明加噪方法无法得到高SSIM 的光谱对，不是生成同步光谱对的有效手段。

3.4 网络层数

为了考察网络层数对伪光谱质量的影响，本文在2层全连接层网络的基础上，将VAE编码器和生成器分别增加一层全连接层，并增加二者的神经元数量。VAE 编码器的3层神经元数量分别为500，300，200；生成器的3层神经元数量分别为200，300，500。

本节比较了2 层VAE-Dual GAN 和3 层VAEDual GAN 的Rs/Fm的VSSIM值以及训练时间，结果如表3 所示，对于每个波长区间，3 层VAE-Dual GAN的Rs/Fm 高于Rs/Rm，但低于2 层VAE-Dual GAN 的Rs/Fm。这说明2 层VAE-Dual GAN 模型生成的伪月球光谱质量高于3 层的VAE-Dual GAN 模型。究其原因，过多的全连接层和神经元数将造成过拟合，进而导致伪光谱质量的下降。此外，表3 显示，2 层VAE-Dual GAN 模型的训练时间比3 层VAE-Dual GAN 模型短约10 000 s。这说明增加全连接层数和神经元数均会使训练时间延长。

表3 网络层数Table 3 The number of network layers

3.5 卷积层与全连接层的对比

为了体现全连接层的优越性，本文将其与卷积层进行对比。基于卷积层的VAE-Dual GAN 的网络结构具体如下：VAE编码器为2层卷积层，生成器为5层转置卷积层和1层卷积层；卷积核大小为3 × 3，通道数为32，步幅为2。

表4给出了2种VAE-Dual GAN 的Rs/Fm的VSSIM值以及伪光谱的径向速度标准差。卷积层VAEDual GAN 的Rs/Fm 略高于Rs/Rm 和全 连接层VAEDual GAN 的Rs/Fm。卷积层VAE-Dual GAN 的径向速度标准差高于全连接VAE-Dual GAN 的径向速度标准差。究其原因，卷积层VAE-Dual GAN 仅关注光谱特征，而非相位。这导致卷积层VAE-Dual GAN Rs/Fm 的结构相似度高于全连接层VAE-Dual GAN，测速精度却低于全连接层VAE-Dual GAN。

表4 卷积层与全连接层Table 4 Convolution layer and fully connection layer

3.6 网络指标对比

为了验证VAE-Dual GAN优于Dual GAN和VAECycle GAN，本文采用SSIM和标准化相对鉴别分数［40］（Normalized relative discriminative score，NRDS）作为对比指标。光谱波长为5 964.872-6 032.103Å。表5 给出了生成的伪行星光谱与真实行星光谱的结构相似度。

表5 GAN模型的VSSIMTable 5 VSSIM of GAN models

VAE-Dual GAN 生成的伪月球光谱与真实太阳光谱的相似度最高，Rs/Rm 最低，这说明3 个模型的伪光谱对在相似度上都有不同程度的提升，并且VAE-Dual GAN 的伪光谱优于VAE-Cycle GAN 和Dual GAN。

NRDS是评判GAN模型优劣的指标。将相同个数的真实光谱和多个GAN 模型生成的伪光谱混合投入一个分类器。经过足够多的训练迭代次数，使分类器可以完全区分出2类光谱样本。当生成伪光谱的概率分布与真实分布高度接近时，分类器很难完全区分。NRDS计算公式为：

式中：A（Ci）为第i个GAN 模型输出曲线Ci围成的面积。TNRDS越高，对应的GAN模型越好。

下 面，考 察VAE-Dual GAN 与Dual GAN 和VAE-Cycle GAN的TNRDS，光谱波长为5 964.872-6 032.103Å。图3给出了各种GAN模型生成的错误率曲线，表6 给出了其对应的TNRDS。从以上结果可以看出，VAE-Dual GAN 的错误率曲线高于另2 个GAN 模型，且VAE-Dual GAN的TNRDS最 大。VAEDual GAN 的伪光谱的区分难度最高，即该模型生成的光谱对质量优于Dual GAN和VAE-Cycle GAN。

表6 GAN模型的TNRDSTable 6 TNRDS of GAN models

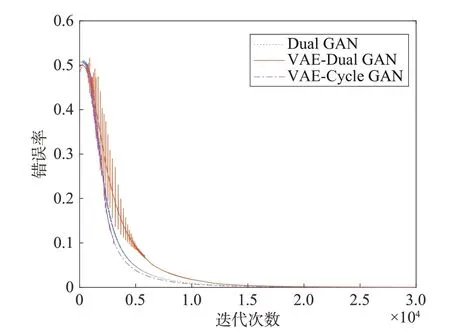
图3 GAN模型的错误率曲线Fig.3 Error rate curves of GAN models

4 结论

天文多普勒差分导航需要同步的太阳光谱和行星光谱，但目前无法满足要求。为此，本文提出一种基于深度学习的太阳/行星光谱对生成方法。为充分利用VAE 的数据增强能力和Dual GAN 的转换学习能力，将二者融合，以生成同步的太阳/伪行星光谱对。实验结果表明，VAE 具有数据增强能力，解决了小样本情况下约束能力较弱的问题。VAE-Dual GAN 的太阳/伪行星光谱对的测速精度和结构相似度均优于真实光谱对、含噪光谱对以及其他GAN生成的光谱对。这说明了VAE-Dual GAN的太阳/伪行星光谱对的质量高。