感应电能传输系统多并联拾取模块电流和输出功率均衡方法

杨继鑫，史黎明，殷正刚，范满义，李耀华

（1.中国科学院电力电子与电气驱动重点实验室（中国科学院电工研究所）,北京市 100190；2.中国科学院大学,北京市 100049）

0 引言

感应电能传输（inductive power transfer,IPT）系统具有安全、方便、可靠性高以及维修费用少等优势［1-2］。国内外对应用于便携式电子设备［3-4］、电动汽车［5-7］以及轨道交通［8-10］等场合的IPT 系统进行了深入的研究。

不同于中小功率的IPT 系统,应用于轨道交通的IPT 系统可达兆瓦级别［11］。受限于功率半导体器件的容量,传统单个拾取模块难以满足轨道交通等大功率应用场合的需求。因此,大功率IPT 系统常采用多拾取模块并联的方法［12］。

理想情况下,发射线圈与各个拾取线圈之间的互感、各个拾取线圈的自感以及拾取线圈的内阻均相同。因此,各个拾取模块的电流与输出功率相同。然而,由于实际中不可避免的制作误差和安装误差以及列车运行过程中的转弯、晃动等因素,拾取线圈的自感、内阻以及发射线圈与拾取线圈之间的互感将产生相对差异,会导致各个拾取模块的电流和输出功率不均衡,从而降低系统效率,严重时甚至会导致某个拾取模块过流而造成系统故障。因此,有必要对多并联拾取模块的IPT 系统的电流和输出功率均衡方法进行研究。

文献［13］提出在拾取侧采用半控整流器替代不控整流器,或者在拾取侧增加Buck/Boost 变换器。通过控制半控整流器或者Buck/Boost 变换器实现各个拾取模块交流侧的等效电阻变换,从而实现各个拾取模块的电流均衡。但是,该方法并没有实现各个拾取模块的输出功率均衡,会造成各个拾取模块的功率半导体器件的使用寿命不一致。同时,采用半控整流器或者增加Buck/Boost 变换器会提高系统造价和控制复杂性。文献［14］提出采用全控整流器替代不控整流器,从而实现了多并联拾取模块的电流和输出功率均衡。但是,系统造价和控制复杂性将会显著提高。文献［15-16］提出通过调整拾取线圈之间的互感以实现各个拾取模块的电流和输出功率均衡。该方法简单,无须添加任何额外的设备。但是,当互感变化时,需要重新调节拾取模块之间的互感。此外,文献［16］提出可通过调节拾取模块的补偿电容器,使拾取模块失谐,从而实现电流和输出功率均衡。但是,该方法会增加系统的无功分量,从而降低系统效率。文献［17］提出一种实时调节拾取模块补偿电容器的方法。但是,该方法调节时间较长,并且同样会降低系统效率。

为实现多并联拾取模块的电流和输出功率均衡,降低拾取模块过流甚至系统故障的风险,本文提出一种基于并联拾取模块补偿电容器的多并联拾取模块电流和输出功率均衡方法。首先,分析了传统IPT 系统和所提IPT 系统拓扑的特性；然后,进一步研究了互感、拾取线圈自感以及拾取线圈内阻对电流分布以及系统效率的影响；最后,通过4 个并联拾取模块的IPT 系统实验平台验证了所提方法的有效性。

1 IPT 系统拓扑

传统具有多并联拾取模块的IPT 系统拓扑如图1 所示［8］。图中：Vdc为直流电压源：vab为高频逆变器的输出电压：ip为发射线圈电流：isi为第i个拾取模块的电流,i=1,2,…,n,其中,n为拾取模块数量；vcdi为第i个不控整流器的输入电压；Vo为输出直流电压；Lp、Cp、rp分别为发射线圈、补偿电容器和发射线圈 内 阻；Lsi、Csi、rsi分 别 为 第i个 拾 取 模 块 的 拾 取 线圈、补偿电容器和拾取线圈内阻；Mi为发射线圈与第i个拾取线圈之间的互感；Coi为第i个拾取模块的输出直流电容器；R为负载；S1、S2、S3、S4为绝缘栅双极型晶体管（insulated gate bipolar transistor,IGBT）；Di1、Di2、Di3、Di4为 第i个 不 控 整 流 器 的 二极管。

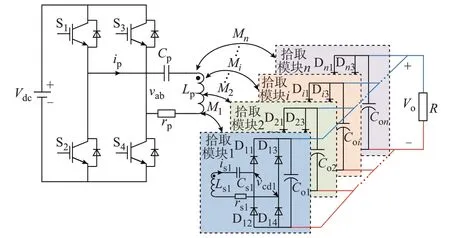
图1 传统具有多并联拾取模块的IPT 系统拓扑Fig.1 Topology of conventional IPT system with multiple parallel pickup modules

轨道交通应用场合中,拾取模块沿导轨方向依次排列,拾取线圈之间的距离较长,故拾取线圈之间的互感较小。同时,文献［18-19］指出,拾取线圈之间的互感可以等效为拾取线圈自感的增量,可通过拾取侧补偿电容进行补偿。因此,文中忽略拾取线圈之间的互感。

IPT 系统的自然谐振角频率ω［20-21］满足：

式中：f为系统的自然谐振频率。

为实现多并联拾取模块的电流和输出功率均衡,本文所提多并联拾取模块拓扑如附录A 图A1所示。各个拾取模块的补偿电容器两端通过导线并联连接在一起,即所有拾取模块共用一个补偿电容器,该补偿电容器的容值为所有补偿电容器容值之和。

本文采用基波等效法［22-23］进行分析。因此,提出的多并联拾取模块的基波等效电路如图2 所示。图 中：İp为 发 射 线 圈 电 流ip的 基 波 相 量；İsi为 第i个 拾取模块电流isi的基波相量；İoi为不控整流器的输入电流ioi的基波相量；Re为交流等效电阻,Re=（8/π2）R。

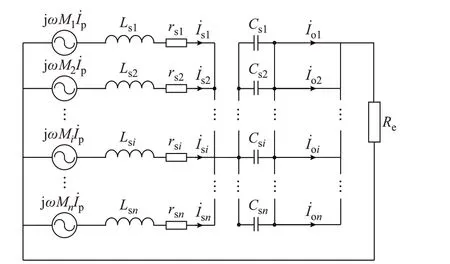
图2 本文所提多并联拾取模块等效电路Fig.2 Equivalent circuit of proposed multiple parallel pickup modules

忽略不控整流器的损耗,由图2 可知,所有补偿电容器的输出电流相当于流经n条并联导线。因此,不控整流器的输入电流可实现自动均衡,即İo1=İo2=…=İoi=…=İon。由 于 各 个 拾 取 模 块的输出端并联连接,不控整流器的输入电压相等。于是,各个拾取模块的输出功率实现自动均衡。

本文通过叠加原理求解İsi。由图2 可知,当jωMi İp单 独 作 用 时,所 提 多 并 联 拾 取 模 块 的 自 阻抗为：

因 此,可 得İsi的 表 达 式 为：

其中,Ziq（i≠q）为第i个与第q个拾取模块之间的互阻抗,其表达式如下：

式中：

2 电流比与系统效率分析

2.1 电流比分析

本文提出的两并联拾取模块的IPT 系统的基波等效电路如图3 所示。图中：V̇ab为高频逆变器输出电压vab的基波相量。

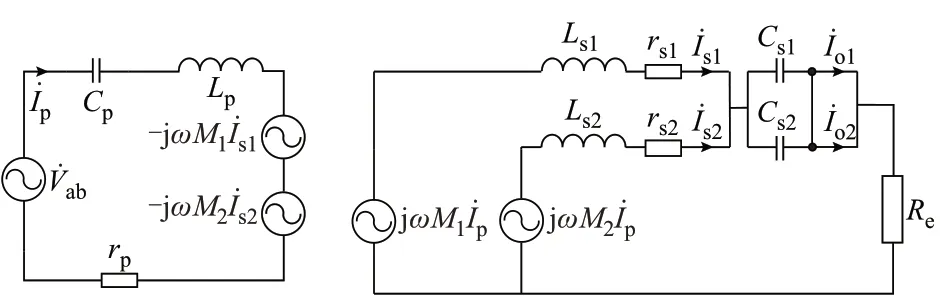
图3 本文所提两并联拾取模块的IPT 系统等效电路Fig.3 Equivalent circuit of proposed IPT system with two parallel pickup modules

根据图3 及式（2）,Z1、Z2、Z12、Z21可以表示为：

根据式（5）—式（8）,可得İs1、İs2的表达式为：

传统两并联拾取模块的IPT 系统的基波等效电路如图4 所示［13］。图中：蓝色虚线框中的等效电路可由红色虚线框的等效电路演变而来；İpt为发射线圈 电 流 的 基 波 相 量；İs1t、İs2t分 别 为 传 统IPT 系 统 第1和第2 拾取模块的电流的基波相量；Re1、Re2分别为传统IPT 系统第1 和第2 拾取模块的交流等效电阻。

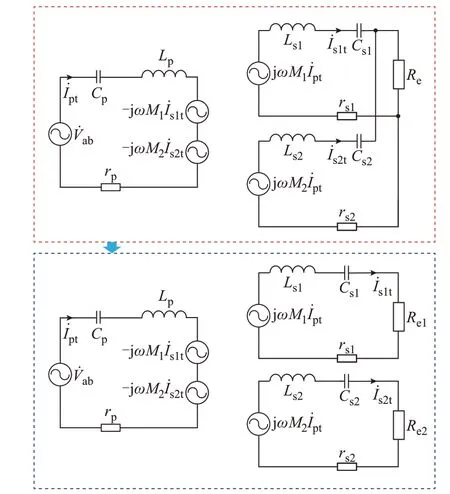
图4 传统两并联拾取模块的IPT 系统等效电路Fig.4 Equivalent circuit of conventional IPT system with two parallel pickup modules

根据基尔霍夫电压定律,传统IPT 系统可表示为：

由于2 个拾取模块的输出端并联,不控整流器的输入电压满足如下关系：

根据式（12）、式（13）,Re1、Re2可以表示为：

于 是,可得İs1t、İs2t的表 达式为：

式中：g1、g2为常系数。

本文定义k为两个互感之比,即k=M1/M2；α为两个拾取线圈自感之比,即α=Ls2/Ls1；δ为两个拾取线圈内阻之比,即δ=rs2/rs1。

根据式（9）、式（10）,可得本文所提IPT 系统的电流比β的表达式为：

根据式（15）、式（16）,可得传统IPT 系统的电流比β′的表达式为：

第1 拾取模块的参数如表1 所示。

表1 第1 拾取模块参数Table 1 Parameters of the first pickup module

首先,假设α=1、δ=1,不同负载下传统IPT 系统和本文所提IPT 系统的电流比随k变化的曲线分别如图5（a）和（b）所示。由图5 可知,互感不一致时,传统IPT 系统中各个拾取模块的电流不均衡,并且随着负载增加,电流不均衡情况会更加严重,甚至会导致某个拾取模块过流而造成系统故障。然而,采用本文所提IPT 系统时,各个拾取模块的电流可实现均衡,电流比为1,故拾取模块过流的风险可以显著降低。

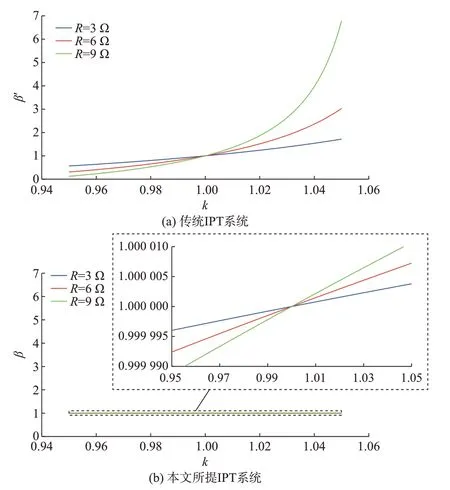
图5 不同负载下不同IPT 系统的电流比随互感比k 变化的曲线Fig.5 Curves of current ratio of different IPT systems varying with mutual inductance ratio k under different loads

由式（18）可知,谐振状态下,传统IPT 系统中拾取线圈自感的差异不会影响电流均衡。因此,文中只对拾取线圈自感差异对所提IPT 系统的电流比的影响进行分析。

假设k=1、δ=1,不同负载下本文所提IPT 系统的电流比随α变化的曲线如附录A 图A2 所示。由图A2 可知,β与α近似呈线性关系。实际中,拾取线圈自感之间的差异不会超过5%,甚至更小。因此,采用本文所提方法时,拾取线圈自感之间的差异对电流均衡的影响很小。

假设k=1、α=1,不同负载下传统IPT 系统和本文所提IPT 系统的电流比随δ变化的曲线分别如附录A 图A3（a）和（b）所示。由图可知,当采用传统IPT 系统时,β′与δ近似呈线性关系。采用本文所提方法时,电流比β为1,内阻不一致不会影响电流的均衡。

由上述分析可知,采用本文所提方法时,可以较好地解决由于各个拾取模块之间参数不一致造成的电流不均衡现象,从而减小拾取模块过流甚至系统故障的风险。

对于本文所提IPT 系统而言,根据式（17）推导可知,当（ωLs1/rs1）≤（2β/|1-β2|）时,k有解,否则k无解。实际中,为减小线圈损耗,发射线圈和拾取线圈均采用利兹线进行绕制,所以,ωLs1≫rs1,一般（ωLs1/rs1）>100。因此,只有当电流比β趋于1 时,k才有解,否则k无解,即互感参数不一致并不会影响多并联拾取模块电流和输出功率均衡的实现。由表1 可知,假设可接受的电流比β的取值范围为0.9～1.1,则拾取线圈自感比α的取值范围为0.9～1.1；拾取线圈内阻差异需满足|rs2-rs1|≤84.16。

综上,当采用本文所提方法时,无须考虑互感参数差异对多并联拾取模块电流和输出功率均衡的影响,并且拾取线圈自感以及内阻的误差范围在实际制作中很容易满足。因此,可有效减小系统设计制造难度,进一步提高系统可靠性。

2.2 系统效率分析

效率是衡量IPT 系统性能的重要指标［24-26］。由图3 可得,本文所提IPT 系统的效率为：

式中：Po、Pi分别为本文所提IPT 系统的输出功率和输入功率。

由图4 可得,传统IPT 系统的效率为：

式中：Pot、Pit分别为传统IPT 系统的输出功率和输入功率。

定义系统效率比e为：

假设α=1、δ=1,不同负载下效率比e随互感之比k变化的曲线如图6（a）所示。由图可知,互感不一致时,本文所提IPT 系统的效率高于传统IPT 系统,并且随着负载的增加,所提IPT 系统的效率提升会更加明显。

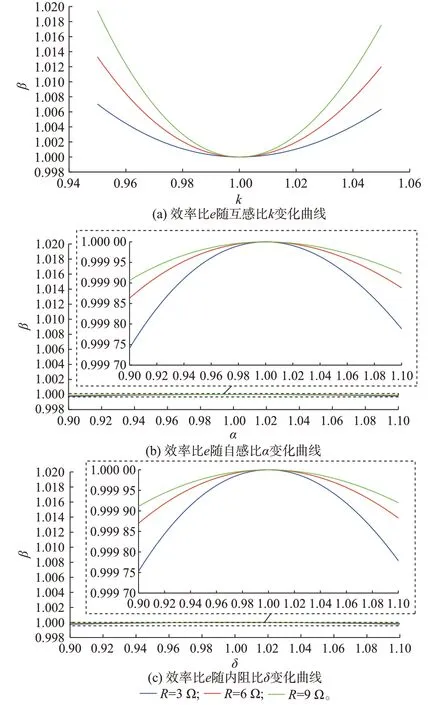
图6 不同负载下效率比e 随互感比k、自感比α 和内阻比δ 变化的曲线Fig.6 Curves of efficiency ratio e varying with mutual inductance ratio k, self-inductance ratio α and internal resistance ratio δ under different loads

假设k=1、δ=1,不同负载下效率比e随自感之比α和内阻之比δ变化的曲线如图6（b）和（c）所示。由图可知,当拾取线圈自感以及拾取线圈内阻不一致时,本文所提IPT 系统的效率略低于传统IPT 系统。但是,随着负载增加,本文所提IPT 系统效率与传统IPT 系统效率趋于一致,效率比e几乎为1。

综合以上分析,采用本文所提方法时,可以实现各个拾取模块的电流和输出功率均衡,从而降低拾取模块过流甚至系统故障的风险,并且可以有效提高系统的效率。

3 实验验证

本文分别采用传统IPT 系统和所提IPT 系统进行实验验证,并分别对比了拾取模块电流和输出功率均衡性能以及系统效率。

附录B 图B1 所示为中速磁浮列车IPT 系统实验装置。实验装置结构图如附录B 图B2 所示,耦合机构原理图如附录B 图B3 所示。由图可知,原边侧包括三相不控整流器以及3 套高频逆变器,高频逆变器的输出端通过匹配变压器串联,然后与发射线圈和补偿电容器连接；副边侧包含4 个拾取模块。发射线圈匝数为2 匝,且不铺设铁氧体；为获得期望的输出电压,拾取线圈绕制匝数较多,为34 匝,且拾取线圈上方铺设铁氧体以减少漏磁,进一步提高输出电压。IPT 系统参数如表2 所示。高频逆变器采用移相控制,且移相角为0°,高频逆变器工作频率为29.1 kHz。

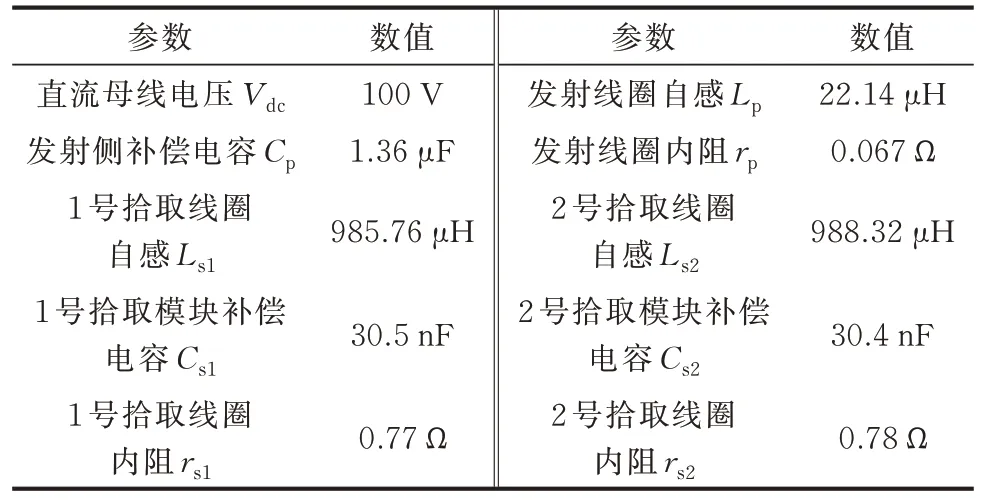
表2 IPT 系统参数Table 2 Parameters of IPT system

首先,选取1 号拾取模块和2 号拾取模块以验证本文所提方法的有效性。 当k=M1/M2=16.73 μH /16.05 μH=1.04 时,不 同 负 载 下,传 统IPT 系统和本文所提IPT 系统实验波形分别如附录B 图B4、图B5 所示。

传统IPT 系统和本文所提IPT 系统的拾取模块电流的有效值和系统效率实验数据如表3 所示。表中：Is1t、Is2t、Is1、Is2分别为İs1t、İs2t、İs1、İs2的有效值。

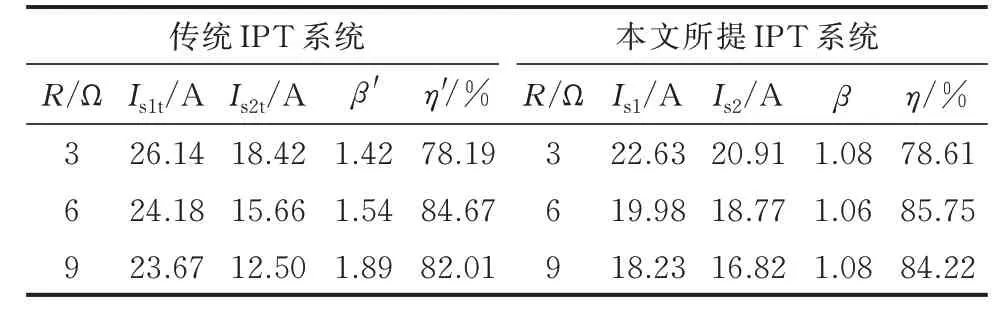
表3 不同IPT 系统的拾取模块电流和系统效率Table 3 Pickup module currents and system efficiencies of different IPT systems

由附录B 图B4、图B5 以及表3 可知,由于参数不一致,传统IPT 系统中2 个并联拾取模块的电流并不相同。然而,本文所提IPT 系统中2 个并联拾取模块的电流和输出功率可实现基本一致。电流比最大减少了81%,效率最高提升了2.21%。

不同负载下,系统效率比e随k变化的实验结果如图7 所示。由图可知,本文所提IPT 系统效率高于传统IPT 系统,随着负载增加,系统效率的提升更加明显。当R=9 Ω 时,系统效率最高提升了2.21%。

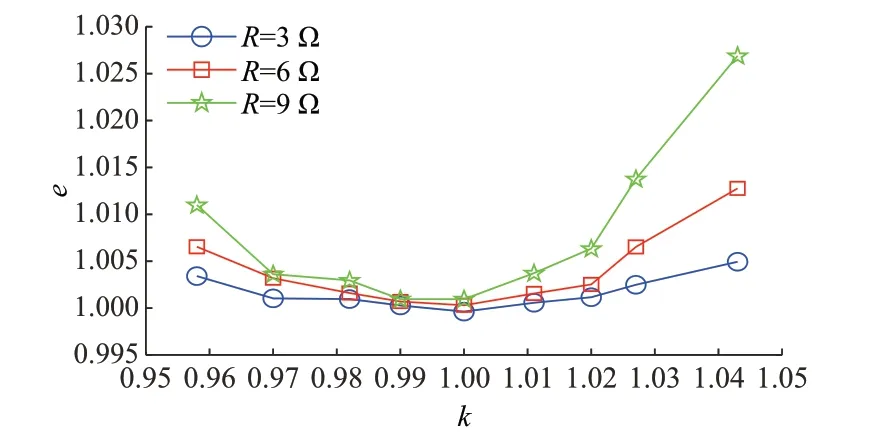
图7 不同负载下效率比e 随互感比k 变化的实验结果Fig.7 Experimental results of efficiency ratio e varied with mutual inductance ratio k under different loads

当R=9 Ω,副边侧采用4 个并联拾取模块时,传统IPT 系统和本文所提IPT 系统的实验波形如图8所示。由图可知,传统IPT 系统4 个拾取模块的电流有效值分别为21.21、7.58、1.10、0.29 A；本文所提IPT 系统4 个拾取模块的电流有效值分别为7.79、7.66、7.83、7.79 A,拾取模块电流和输出功率基本一致。

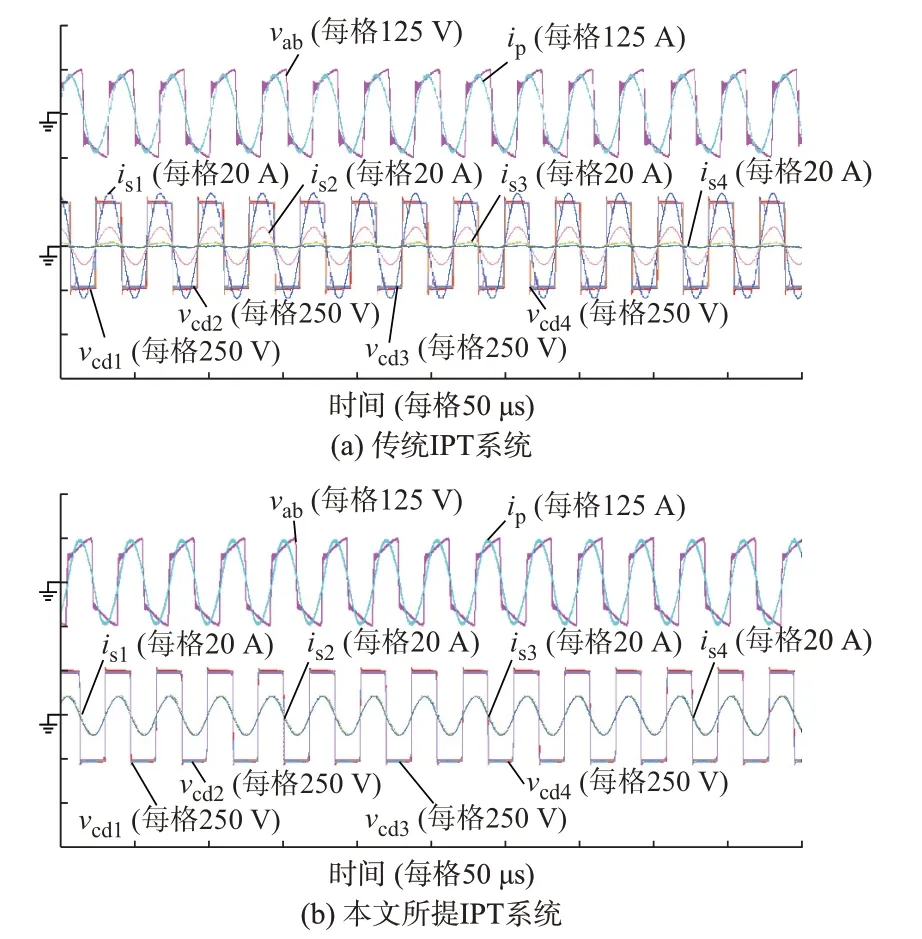
图8 副边侧采用4 个并联拾取模块时不同IPT 系统的实验波形Fig.8 Experimental waveforms of different IPT systems with four parallel pickup modules on secondary side

实验结果与理论分析一致,由此可证明本文所提方法的有效性。

4 结语

针对参数不一致造成的多并联拾取模块电流和输出功率不均衡的问题,本文提出一种基于并联拾取模块补偿电容器的电流和输出功率均衡方法,无须增加任何硬件电路以及复杂的控制策略。通过理论分析与实验验证,得到如下结论：

1）采用本文所提方法时,可实现多并联拾取模块的电流和输出功率均衡,降低因参数不一致而导致的模块过流甚至系统故障的风险,提高系统可靠性；

2）相比传统IPT 系统,本文所提方法可以有效提高系统效率。当R=9 Ω 时,系统效率最高提升了2.21%。

本文所提多并联拾取模块电流与输出功率均衡方法可为大功率轨道交通IPT 系统设计提供一定的借鉴。此外,某一拾取模块的补偿电容器发生故障后,对系统进行相应的容错运行控制将是下一步的研究方向。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。