考虑不同需求弹性的爬坡辅助服务市场出清模型
赵 越,蔡秋娜,王 龙,戴晓娟,王泽林,邹文滔
(1.广东电网有限责任公司电力调度控制中心,广东省广州市 510600;2.北京清能互联科技有限公司,北京市 100080)
0 引言
随着新能源在电力系统中的渗透率不断提高,电力系统净负荷急剧拉升或下降的情况愈加明显,如 美 国 加 州 净 负 荷 所 呈 现 的“鸭 型 曲 线”[1]。“十 三五”期间,中国新能源装机占比提升了13%,而抽水蓄能、调峰气电等传统调节电源占比却维持不变[2]。新型电力系统背景下,中国灵活性资源的建设愈加迫切。
现阶段,部分新能源发展较快的国外电力市场已建设爬坡辅助服务市场品种,如美国加州的灵活性爬坡产品(flexible ramping product,FRP)[3-4]、美国中部电力市场的爬坡能力产品(ramping capability product,RCP)[5]、英 国 的 快 速 备 用(fast reserve,FR)等。美国加州电力市场在爬坡市场中只采购不确定爬坡需求量,并已从之前采用概率密度分布转变到如今采用概率密度和分位数回归结合方法计算多段未采购弹性爬坡需求价格曲线[6]。美国中部电力市场在爬坡市场中采购确定性与不确定性爬坡需求,从刚开始的单段需求曲线改进到现阶段的多段弹性爬坡需求曲线[7],在需求价格确定时主要考虑不同爬坡需求曲线对市场价格及主体利益的影响。美国加州和中部电力市场均采用爬坡与电能量、调频、备用联合出清方式。英国在月度市场中主要按投标价格排序开展快速备用品种的出清。
现阶段,中国以试点方式发展电力现货市场,已有多个省份开展电力现货市场结算试运行[8]。中国在最新印发的《电力辅助服务管理办法》[9]中已将爬坡纳入辅助服务品种体系,但各省尚无针对爬坡辅助服务品种的市场出清、补偿等机制或方法。文献[10]介绍了美国加州应对新能源出力不确定性的FRP;文献[11]介绍了FRP 的优化调度与市场机制;文献[12]通过介绍国外电力系统RCP 的市场设计方式及运用效果,对比总结灵活性爬坡能力的不同获取方式。文献[13]提出在日前市场采购FRP的方法,采用随机机组组合模型最优解设定爬坡需求,在日前市场出清环节进行市场出清得到电能量和爬坡价格。文献[14]提出一种基于惩罚因子的方法以缓解因采购爬坡容量导致的电力成本上涨情况。文献[15]为实时市场出清模型设计了激励相容的定价方法以满足净负荷变动需求,但未解决净负荷不确定问题。
上述文献着重从工业界的角度研究爬坡算法、优化问题,较少结合市场环境发展的实际情况来研究。同时在实践中,美国加州和中部电力爬坡市场的爬坡需求弹性都较大,可保证较高的市场整体经济性,但给电网运行安全带来了更大的挑战。针对要求市场平稳起步的中国电力市场,本文从中国现阶段电力市场实际情况出发,考虑爬坡需求弹性,对爬坡辅助服务市场的分阶段出清模型、发展路径进行了研究。
1 爬坡需求曲线计算方法
1.1 确定性与不确定性爬坡需求
FRP 旨在解决由预测的净负荷变动和负荷预测误差导致的电力不平衡问题。因此,采购的FRP总需求分为确定性爬坡需求和不确定性爬坡需求2 部分,其组成分别如式(1)、式(2)所示。
式 中:t为 当 前 时 段;RFRU,t和RFRD,t分 别 为 系 统 上 爬坡和下爬坡总需求量;RFRU,D,t和RFRD,D,t分别为确定性上爬坡和下爬坡需求;RFRU,U,t和RFRD,U,t分别为不确定性上爬坡和下爬坡需求。
RFRU,D,t和RFRD,D,t由系统内的净负荷变化造成,RFRU,U,t和RFRD,U,t由在特定置信区间内系统净负荷预测误差造成。RFRU,D,t和RFRD,D,t的计算如式(3)至式(5)所示。
式中:Dt和Dt+1分别为当前时段t和时段t+1 的系统净负荷预测值;ΔDt为时段t至t+1 间的系统净负荷预测变动值。
系统净负荷预测的误差值与典型日(工作日、星期六、星期日、节假日)、具体时段紧密相关。因此,以某一固定的系统净负荷预测偏差率为间隔,统计相同典型日、相同时段在各系统净负荷预测偏差率间隔范围内出现的频率。该频率可作为概率使用。将系统净负荷预测偏差率乘以时段t的净负荷预测值,得到该时段负荷预测误差的概率密度分布函数。若系统净负荷预测值为1 000 MW,以2%的系统净负荷预测偏差率为间隔,则预测误差概率直方分布如图1 所示。

图1 系统净负荷预测误差概率直方分布Fig.1 Probability histogram distribution of system net load forecasting error
不确定性爬坡需求按式(6)至式(11)计算。
式中:e为系统净负荷预测误差,其等于实际值减去预测值;pt(e)为基于概率直方分布图得到的系统净负荷预测误差概率密度分布函数;PUP,t和PDN,t分别为对应置信区间上限和下限的负荷预测误差(可能为正值或负值);λCLU为概率密度分布函数从负无穷积分到PUP,t的值,即为置信区间上限,例如,99%;PUP,P,t为对应置信区间上限的负荷预测正误差(正值);λCLD为概率密度分布函数从负无穷积分到PDN,t的值,即为置信区间下限,例如,1%;PDN,N,t为对应置信区间下限的负荷预测负误差(负值)。
1.2 多段弹性爬坡需求价格曲线
根据上述爬坡需求确定规则和系统净负荷预测误差概率直方分布图,制定出爬坡需求曲线,曲线上的任一点均表示在不采购一定数量上爬坡或下爬坡容量(RFRU,S,t或RFRD,S,t)的情况下会造成的期望损失,其中,RFRU,S,t为未采购的上爬坡容量,RFRD,S,t为未采购的下爬坡容量。根据图1 的组距(区间距离)对需求价格曲线进行分段划分,当爬坡未采购容量等于需求价格曲线的同一区间内任意值时,其所造成损失的概率相同。
以上爬坡为例,当RFRU,S,t在0 至RFRU,U,t时,根据图1 的各区间系统净负荷预测误差的概率密度分布函数计算其在需求价格曲线的不同区间内所造成损失的概率,再乘以电能量市场投标价格上限,得到因上爬坡不足而可能损失的电能量市场价值,并将爬坡不足时的参考价格作为需求曲线的价格上限。未采购一定数量上爬坡的期望损失为各分段RFRU,S,t对应的爬坡需求价格。 当RFRU,S,t大于RFRU,U,t时,无法满足确定性爬坡需求,必然造成负荷不平衡损失,故将需求价格设置为爬坡不足时的参考价格。
由于PUP,P,t不一定可以被区间距离d整除,故需求价格曲线首段的区间长度不一定为d。根据式(12)计算该需求价格曲线首段长度。
式中:dFRU,t为不考虑RFRU,U,t的上爬坡需求价格曲线的首段长度,且0 因此,需求价格曲线的首段起点为0,终点为dFRU,t,而该段的需求曲线价格则按式(13)计算。 式中:CFRU,t(RFRU,S,t) 为上爬坡需求价格曲线;CFRU,max为上爬坡不足时的参考价格,即上爬坡需求价格上限;Cenergy,max为电能量现货市场投标价格上限。 CFRU,max同时也是爬坡出清价格上限,表示若增加额外1 MW 爬坡需求的成本大于爬坡需求价格上限,则系统将不会额外采购1 MW 的爬坡容量以满足更多的爬坡需求。CFRU,max会影响爬坡出清价格及出清容量,若其值越大,则出清价格和出清容量也越大。在各类辅助服务未与电能量联合出清的电力市场建设初期,可采用市场模拟方法计算不同CFRU,max设置值对应的市场成本及用户分摊费用。考虑市场主体接受程度,设置合适的CFRU,max取值。在调频、备用、爬坡和电能量等各品种采用联合出清方式后,增加考虑各辅助服务之间的重要程度与其需求价格上限的关系,以设置CFRU,max取值,如按重要性排序为向上调频≻正备用≻上爬坡,则存在式(14)的关系。 式中:CResP,max和CRegU,max分别为正备用和向上调频的需求价格上限,也为容量不足时的松弛价格。 各类品种需求价格上限表征各类品种的重要程度。在各品种联合出清方式下,可在电力资源紧张时期决定市场在各品种间的取舍顺序,需求价格上限越低的品种,越先被削减出清量。在dFRU,t≤RFRU,S,t 采用式(13)、式(15)计算RFRU,S,t所在区间的概率密度分布函数积分时会乘0.5,这是因为RFRU,S,t可能等于该区间内的任意值,而令RFRU,S,t等于该区间中间值时计算出的期望损失整体误差最小。因为系统净负荷预测误差概率密度分布函数为直方分布图,所以在同一预测误差区间内,发生不同水平预测误差的概率是相同的,从而可取该区间预测误差概率的一半。 与上爬坡需求价格曲线的计算方法相同,下爬坡需求价格曲线的首段长度计算如式(17)所示。 式中:dFRD,t为下爬坡产品需求价格曲线的首段长度,且-d≤dFRD,t<0;rFRD,t为图1 中负误差区间终点不小于PUP,P,t的区间数量。 需求价格曲线的首段起点为0,终点为dFRD,t,而该段的需求曲线价格则按式(18)计算。 式中:CFRD,t(RFRD,S,t) 为下爬坡需求价格曲线;CFRD,max为下爬坡不足时的参考价格,即下爬坡需求价格上限;Cenergy,min为负的深度调峰辅助服务市场价格上限或负的深度调峰补偿价格上限。 在电力市场发展后期,若电能量现货市场允许申报负电价,则Cenergy,min可取电能量现货市场投标价格下限。CFRD,max的具体设置方式可参考CFRU,max的设置方法,在各类辅助服务未与电能量联合出清的电力市场初期,采用市场模拟方法计算不同CFRD,max设置值对应的市场成本及用户分摊费用,考虑市场主体接受程度,设置合适的CFRD,max取值。在电力市场机制逐步完善,调频、备用、爬坡和电能量等各品种采用联合出清方式后,增加考虑下爬坡与调频、深度调峰等产品的重要度与其需求价格上限的关系,设置CFRD,max的值,如按重要性排序为向下调频≻负备用≻下爬坡,则存在式(19)的关系。 式中:CResN,max和CRegD,max分别为负备用和向下调频的需求价格上限,也为容量不足时的松弛价格。 在dFRD,t≥RFRD,S,t>RFRD,U,t区间内,除首段外,其余每段的需求价格曲线起点为dFRD,t-d(nFRD,t-2),终 点 为dFRD,t-d(nFRD,t-1);在RFRD,U,t≥RFRD,S,t区间内,需求价格曲线起点为RFRD,U,t,终点为RFRD,t。其中,nFRD,t为在RFRD,S,t>RFRD,U,t区间内除首段外需求价格曲线的每段序号,且2 ≤nFRD,t≤rFRD,t+1。后续几段爬坡需求曲线的价格计算如式(20)、式(21)所示。 绘制上爬坡和下爬坡需求价格曲线,如图2 所示。随着未被采购的上爬坡容量增加,计划采购的上爬坡容量被压减,其无法覆盖的系统净负荷预测误差增大。由于系统净负荷预测误差造成负荷不平衡的概率越来越大,故表征在需求曲线上有可能造成的负荷不平衡损失(由需求曲线价格表示)也不断增长。 图2 多段爬坡需求价格曲线Fig.2 Ramping demand-price curve of multiple segments 单段弹性爬坡需求价格曲线只考虑爬坡采购量大于确定性爬坡需求与一定置信水平下不确定性爬坡需求加和后的价值。 上爬坡和下爬坡的需求价格曲线的计算方式分别如式(22)、式(23)所示。 式中:RFRU,A,t和RFRD,A,t分别为出清的上爬坡、下爬坡容量;CFRU,A,t(RFRU,A,t)和CFRD,A,t(RFRD,A,t)分别为单段上、下爬坡需求价格曲线。 爬坡需求的单段爬坡需求价格曲线如图3所示。 图3 单段爬坡需求价格曲线Fig.3 Ramping demand-price curve of single segment 采用快速爬坡辅助服务市场与电能量市场、调频辅助服务市场联合出清方式,实现系统总体成本最小化。为简化表述,下述模型只考虑与电能量市场的联合优化。 1)模型1 模型1 的目标函数不考虑爬坡需求价值,约束条件考虑爬坡最小需求,其数学描述如式(24)和式(25)所示。 式 中:Ek,i,t和θk,i,t分 别 为 机 组i在 时 段t的 第k段 电能量市场中标量和报价;Ei,t为机组i在时段t的电能量市场中标量;RFRD,A,i,t和RFRU,A,i,t分别为机组i在时段t的下爬坡和上爬坡中标量;Emax,i,t和Emin,i,t分别为机组i在时段t的容量上限和容量下限;ρUpR,i和ρDnR,i分别为机组i的上爬坡和下爬坡速率;l为优化时段长度,一般为15 min。 该模型的RFRU,t和RFRD,t均考虑了确定性爬坡需求和一定置信水平下的不确定性爬坡需求。置信水平越高,系统防范不确定风险的能力越大。 2)模型2 模型2 的目标函数考虑单段爬坡需求价值,约束条件考虑爬坡最小需求,其数学描述如式(25)至式(27)所示。 模型2 的最小爬坡约束值可设置为确定性爬坡需求与一定置信水平下的不确定性爬坡需求的加和,且置信水平一般可取比模型1 计算最小爬坡需求时考虑的置信水平更小的数值。 3)模型3 模型3 的目标函数考虑多段爬坡需求价值,约束条件考虑爬坡最小需求,其数学描述如式(26)和式(28)所示。 在充分竞争的市场中,一般会以商品的价值来定价。价值定价模式下爬坡辅助服务市场一般不考虑爬坡成本,而以系统爬坡边际价格作为爬坡统一出清价格,在出清模型中体现为爬坡需求约束的影子价格。只有模型中的爬坡需求约束达界时,爬坡出清价格才不为零。以边际定价方式得到系统统一的爬坡价格,更能反映爬坡的供需紧张程度,激励市场主体在电力供应紧张时积极提供爬坡容量,对市场的适应性较强。 模型1 和模型2 的爬坡价格为其最小爬坡需求的影子价格,模型3 的爬坡价格为爬坡采购量与未采购量大于或等于爬坡需求(可取与模型1 最小爬坡需求相等的值)的影子价格。 1)对于模型1,爬坡价格为增加单位爬坡需求增加的电能量市场成本。在爬坡需求不紧张时,增加爬坡需求不需调整电能量市场机组出力,此时,系统将相比最小爬坡需求多采购爬坡容量,即最小爬坡需求约束未达界,爬坡价格为零;在爬坡需求较为紧张时期,增加爬坡需求需增加高价机组出力和降低低价机组出力,此时,爬坡价格为增加电能量出力机组的电能量市场报价与压减电能量出力机组电能量市场报价的差值。 2)对于模型2,若增加单位爬坡需求无需调整机组电能量市场出力,或所增加的电能量市场成本(即增加出力的高价机组报价与减少出力的低价机组报价之差)不大于爬坡需求价格,则系统将相比最小爬坡需求多采购爬坡容量,即最小爬坡需求约束未达界,爬坡价格为零;反之,最小爬坡约束将达界,爬坡价格为增加单位爬坡需求时,增加电能量出力机组的电能量市场报价与压减电能量出力机组电能量市场报价、爬坡需求价格的差值。 3)对于模型3,未对爬坡采购量直接限制最小需求量,电能量市场采用多时段联合优化隐含了各时段爬坡采购量需不小于确定性爬坡需求的限制。爬坡价格只有在爬坡采购量与未采购量之和大于爬坡需求(与模型1 爬坡需求相同),即爬坡采购量大于爬坡需求时,爬坡价格才为零。当爬坡采购量与未采购量之和约束达界时,若增加单位爬坡需求,则系统可采用2 种方式实现:一是调整电能量市场机组出力方式,即增加高价机组出力而降低低价机组出力,进而增加电能量市场发电成本;二是不调整电能量市场机组出力,增加的爬坡需求作为未采购量,进而增加对应爬坡损失成本(弹性需求曲线对应段的价格)。对比2 种方式的系统成本增加量,并选择其中一种系统成本最低的方式来出清市场。爬坡采购量与未采购量之和约束达界时,爬坡价格取增加电能量出力机组的电能量市场报价与压减电能量出力机组电能量市场报价、相应爬坡需求价格的最小值。 考虑到单段爬坡弹性需求曲线绘制是多段爬坡弹性需求曲线绘制方法的简化,故只考虑多段爬坡弹性需求曲线的绘制。 t时段和t+1 时段系统净负荷预测值分别为1 000 MW 和1 150 MW。电能量现货市场投标价格上限为1 000 元/(MW∙h)。上爬坡和下爬坡不足时的参考价格分别为200 元/(MW∙h)和100 元/(MW∙h)。 统计历史2 年内相同典型日、小时时段下的系统净负荷预测误差率在2%区间距离下的出现频次,如表1 所示。计算得到系统净负荷预测误差概率值如表2 所示。 表1 系统净负荷预测误差率的频次分布数据Table 1 Frequency distribution data of system net load forecasting error rate 表2 系统净负荷预测误差的概率分布数据Table 2 Probability distribution data of system net load forecasting error 根据表1 和表2,RFRU,D,t=150 MW,RFRD,D,t=0 MW,设置置信区间为[2%,98%],得到PUP,t=72.23 MW,PUP,P,t= max (0,PUP,t) = 72.23 MW,RFRU,U,t= max (0,PUP,P,t+RFRD,D,t)= 72.23 MW,PDN,t= -70.29 MW,PDN,N,t= min (0,PDN,t) =-70.29 MW,RFRD,U,t=min (0,PDN,N,t+RFRU,D,t)=0 MW。 因确定性和不确定性下爬坡需求均为0 MW,所以系统无下爬坡需求,即无须计算下爬坡需求曲线。上爬坡需求曲线的计算过程如下。 1)当0 MW ≤RFRU,S,t≤72.23 MW时,爬 坡 采购量大于系统确定性上爬坡需求,但小于系统总上爬坡需求。根据系统净负荷预测误差概率直方分布图计算不同上爬坡未采购量范围内的系统损失,即爬坡价值。 当0 MW ≤RFRU,S,t≤12.23 MW 时,RFRU,A,t≥210 MW,则 有CFRU,t(RFRU,S,t)=17 元/(MW∙h);当12.23 MW 2)当72.23 MW 绘制弹性需求价格曲线,如图4 所示。从上述爬坡需求价格曲线的计算方法可以得到以下结果。 图4 上爬坡需求价格曲线Fig.4 Up ramping demand-price curve 1)置信水平下系统净负荷预测误差的前几个预测误差区间的概率加和等于Cenergy,max与CFRU,max的比值时,需求价格达到上限值CFRU,max。因此,爬坡需求价格曲线的分段区间数量与置信水平下系统净负荷预测误差的前几个预测误差区间的概率分布及Cenergy,max与CFRU,max的 比 值 相 关。 2)该方法根据分时段历史系统净负荷预测误差的概率密度分布函数计算爬坡需求价格曲线,考虑了不同时段下系统净负荷预测误差水平有所不同的时段特征。 以IEEE 39 节点系统为例进行分析。时段数设置为1 日96 个时段,系统各时段净负荷、98% 和96%置信水平的各时段不确定爬坡需求如附录A所示,各时段的上爬坡、下爬坡出清价格及系统采购量如附录B 所示。 4.2.1 爬坡出清容量分析 当模型1 价格为0 元/(MW∙h)时,可认为此时爬坡容量较为充足;当模型2 价格不为0 元/(MW∙h)时,可认为此时爬坡容量不足。针对爬坡容量充足和不足2 种情况,3 种模型的爬坡出清结果分别如图5 和 图6 所 示。 从图5 和图6 可以看出,在爬坡充足时,模型1和模型3 的爬坡出清量曲线几乎重合,爬坡出清价格和容量整体关系为模型2>模型1=模型3。主要原因为模型1 和模型3 在98%置信水平的不确定性爬坡需求容量外,均未考虑需求价格或爬坡损失成本,而模型2 在96%置信水平的不确定性爬坡需求容量外,还有一定的爬坡需求价值。在爬坡较为紧张时,爬坡出清价格和容量的整体关系为模型1>模型2>模型3,体现了需求弹性关系为模型3>模型2>模型1。 图5 爬坡容量充足时爬坡出清结果Fig.5 Ramping clearing results with sufficient ramping capacity 图6 爬坡容量不足时爬坡出清结果Fig.6 Ramping clearing results with insufficient ramping capacity 在爬坡容量不足时期,上爬坡容量不足将增大系统失负荷风险,下爬坡容量不足将增加新能源弃电风险。考虑到市场起步阶段,应尽量降低因市场原因造成的系统失负荷和新能源弃电风险,以实现市场平稳起步,在市场起步阶段可应用模型1,保证市场在爬坡紧张时期也能出清足额的爬坡容量,保障用户用电可靠性和新能源消纳。在市场逐步发展成熟后,再逐步过渡采用模型2、模型3。 4.2.2 爬坡出清价格分析 3 种模型的爬坡出清价格如图7 所示。 图7 爬坡出清价格Fig.7 Ramping clearing prices 从图7 可看出,爬坡尖峰价格整体呈现模型1>模型3>模型2 的关系,主要因为在爬坡容量极为紧张时,模型1 无爬坡需求弹性,系统必须高价购买98%置信水平的不确定爬坡容量,爬坡尖峰价格最高;模型2 在96%至98%置信水平的不确定爬坡需求之间存在需求弹性,系统可无代价地直接选择不购买这部分爬坡需求;模型2 在0 至98%置信水平的不确定爬坡需求之间存在需求弹性,系统可选择不购买这部分爬坡需求,但需付出爬坡损失成本,即为采购爬坡容量的价格。 爬坡尖峰价格主要反映爬坡紧张时期系统爬坡资源提供爬坡辅助服务的价值,并作为爬坡结算的依据,进而影响市场主体分摊的爬坡费用。在新能源渗透率不是特别高时,爬坡不足时期的爬坡价格整体也不会太高,可采用模型1 以凸显爬坡价格信号,进而提高爬坡市场对爬坡资源建设的引导作用,同时不会给市场主体增加太大的爬坡费用分摊成本。在新能源渗透率提高后,再考虑采用模型2 和3,以降低爬坡市场出清价格,减少市场主体爬坡费用分摊成本。 4.2.3 电能量市场价格和各市场费用分析及应用建议 对3 种模型的电能量市场价格和各市场费用进行对比的结果分别如表3 和表4 所示。 表3 电能量市场价格对比结果Table 3 Comparative results of electric energy market prices 表4 市场费用对比结果Table 4 Comparative results of market costs 从表3 可以看出,电能量市场平均价格关系为模型1>模型2>模型3,说明爬坡需求弹性越大,在降低电能尖峰价格、防止电能价格多时段过低方面的效果越显著。从表4 可以看出,单从爬坡费用看,模型1>模型3>模型2,但从电能量市场与爬坡市场总费用看,模型1>模型2>模型3,说明爬坡需求弹性越大,采用电能量和爬坡联合优化出清越有利于提高系统整体经济性。 综合表3 和表4 可知,在联合优化电能量与爬坡市场、提高市场整体经济性、降低电能量市场尖峰价格方面,出清模型的爬坡需求弹性越高,相应市场效果越佳。因此,在市场发展成熟阶段,可采用模型2或模型3,以提高市场整体经济效益,适当降低电能量市场的尖峰价格。上述3 种爬坡市场出清模型的优缺点如表5 所示。从模型的复杂度看,模型3>模型2>模型1;从模型的需求弹性看,模型3>模型2>模型1。需求弹性越高,越有利于系统运行经济性的提高。 表5 3 种模型的优缺点Table 5 Advantages and disadvantages of three models 因此,国内爬坡辅助服务市场建设应考虑新能源和电力市场发展阶段,在不同阶段采用不同的爬坡辅助服务市场出清模型,机制设计由简单到复杂。在新能源装机和发电量占比不高、电力现货市场起步阶段,爬坡需求并不明显,为简化市场模式和出清模型,降低爬坡市场总费用,可考虑采用模型1进行电能量市场出清,并计算各机组因提供预留爬坡容量而损失的机会成本作为机组爬坡中标容量的结算价格。在新能源装机和发电量占比达到一定程度,爬坡资源供应在部分时段出现不足,电力现货市场进入稳定运行期时,可考虑采用模型2 进行电能量市场出清,根据市场整体供需情况,弹性出清系统总的爬坡容量,并将爬坡约束影子价格作为爬坡统一出清价格,对机组所提供的爬坡容量进行补偿,激励机组按调度指令执行发电计划。在新能源渗透率较高、爬坡资源供应呈现常态化紧张形势的时期,电力现货市场也发展得比较成熟时,可采用模型3 进行电能量市场出清,并以爬坡约束的影子价格作为爬坡市场边际出清价格,使得爬坡市场出清结果能够最大程度地反映需求弹性,实现系统综合成本最小,并以统一的爬坡市场边际价格激励市场主体提高自身爬坡能力,从而增加系统灵活性。 为提升电力系统灵活爬坡能力,促进新型电力系统安全运行,对电力爬坡辅助服务市场出清模型和定价方法进行了研究,并构建算例对弹性爬坡需求曲线计算流程进行展示。在此基础上,提出考虑不同爬坡需求弹性的3 种爬坡辅助服务市场出清模型,通过IEEE 39 节点算例对3 种爬坡辅助服务市场出清模型的爬坡出清量、价格和市场总费用进行对比分析,验证了增加爬坡需求弹性可提高市场整体经济性。同时,结合中国实际,提出在新能源和电力市场发展不同阶段的爬坡辅助服务市场建设建议。后续将在以下方面对爬坡辅助服务市场进行探索。 1)本文在构建弹性爬坡需求曲线时只考虑了净负荷时段特征,未考虑季节、天气、典型日等对净负荷预测结果的影响,可能会降低系统净负荷预测误差的计算准确度,进而难以准确评估不同容量段的爬坡价值。下一步可分析新能源、电力负荷预测误差的特征和影响因素,采用分位回归、概率预测、机器学习等方法提高净负荷预测误差的预测准确度,从而更加准确评估不同区间爬坡容量的价值。 2)本文在出清模型中未考虑爬坡资源受网络阻塞的影响,不能保证系统预留爬坡资源在系统中的有效性。后续可研究计及通道传输能力的有效爬坡建模与配置方法,如分区设置爬坡容量需求或在出清模型中计算并扣除受网络约束的无效爬坡容量。 本文研究受广东电网有限责任公司科技项目(适应碳达峰目标的广东电力市场关键技术研究,036000KK52220009)资助,谨此致谢! 附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx),扫英文摘要后二维码可以阅读网络全文。
1.3 单段弹性爬坡需求价格曲线
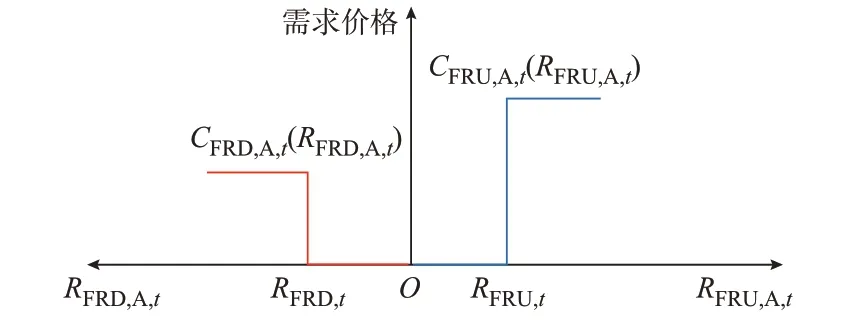
2 快速爬坡辅助服务市场出清模型
3 出清结果分析
4 算例分析
4.1 多段爬坡弹性需求曲线绘制


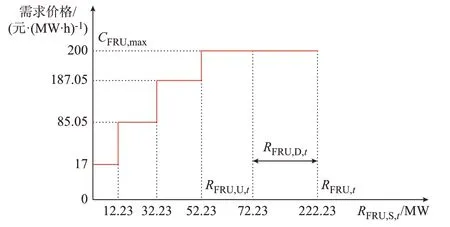
4.2 不同出清模型的仿真分析


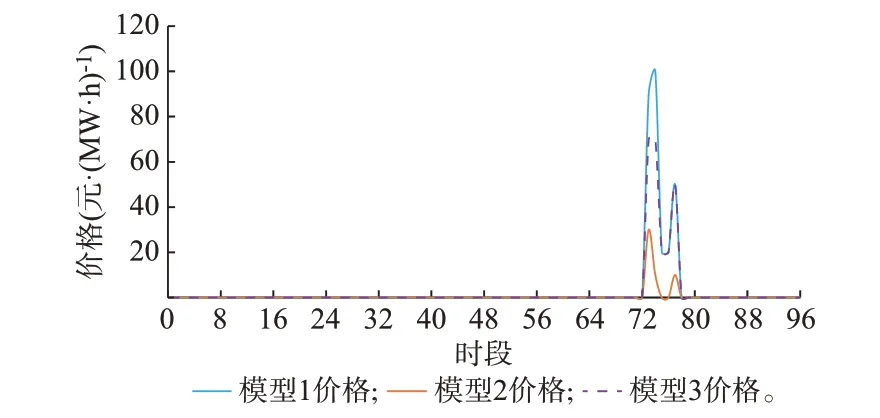
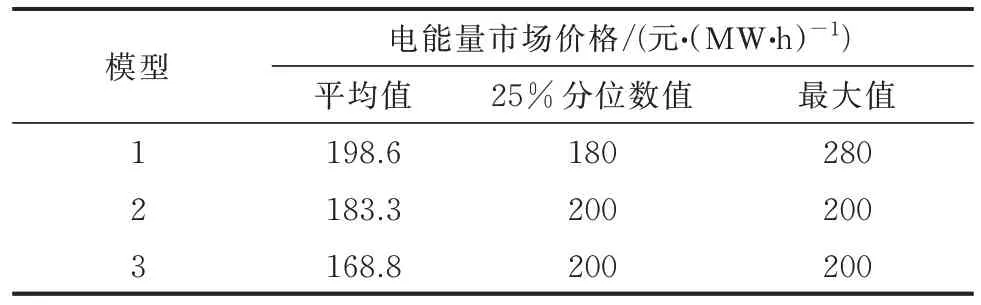


5 结语

