基于BP 神经网络-时间序列模型的中期负荷预测
李梓萍,李校良
(辽宁工程技术大学电气与控制工程学院 辽宁 葫芦岛 125000)
0 引言
电力负荷预测在电力系统中至关重要,分为短期、中期和长期预测,涉及实时运行、规划和决策。 短期预测涵盖数小时至数天,支持实时调度。 中期预测覆盖数周到数月,用于设备维护和容量规划。 长期预测关注一年到数年,影响系统规模和配置。 在之前的研究中,程红利等[1]提出了变分模态分解的中期负荷预测(medium-term load forecasting,MTLF)模型,将负荷序列分解成模态分量,用长短时记忆神经网络建模。 杨洋等[2]提出了极限梯度提升算法(eXtreme gradient boosting,XGBoost)与深度神经网络(deep neural network,DNN)相结合的MTLF 算法,充分利用树模型和深度神经网络,处理交叉特征。 王军[3]则提出了基于深度神经网络的MTLF 方法,强调数据处理。
本研究以BP 神经网络(back propagation neural network,BPNN)模型为基础,处理12 个月的负荷数据,预测次月负荷。 引入时间序列分析,以月为单位处理数据,捕捉短期周期性规律。 通过Matlab 仿真验证,结果表明时间序列分析提升了BP 神经网络的预测准确性,有助于提高电力系统运行效率和决策准确性。
1 基于时间序列分析的算法实现
该模型包括三个核心组成部分:自回归(auto regressive,AR)、差分(irregular,I) 和滑动平均(moving average,MA)。 每个部分都有与之相关的参数,分别是AR阶数(p)、积分阶数(d)和MA 阶数(q)。 这些参数决定了模型考虑的过去观测值数量、差分操作次数以及白噪声误差数量。 AR 部分描述了当前观测值与过去观测值之间的相关性。 AR 阶数(p)指定了要考虑的过去观测值的数量,考虑它们对当前值的影响。 I(差分)部分用于处理时间序列的非稳定性。 积分阶数(d)表示进行的差分操作次数,以使时间序列变得稳定。 MA 部分描述了当前观测值与过去观测值的白噪声误差之间的关系。 MA 阶数(q)决定了要考虑的白噪声误差数量。
2 算法分析
2.1 BP 神经网络模型
BP 神经网络,又称反向传播神经网络,是深度学习中的关键算法。 它包括输入、隐含和输出层,通过梯度下降调整权重和偏差[4],见图1。 输入通过神经元传递,激活函数产生输出。 核心在于反向传播误差,通过计算实际输出与目标输出的误差,逐层反向传播误差,更新权重和偏差,以减小误差并提高性能。 梯度下降用于权重和偏差的调整,最小化误差函数。 通过多次前向传播、反向传播和权重更新迭代,BP 神经网络逐渐适应训练数据,提高泛化能力。

图1 BP 神经网络拓扑结构
参考图1,ωi、ωj代表输入层与隐含层间的权重、隐含层与输出层间的权重,X 代表输入量,y代表神经网络输出量,Y 代表数据实际值,E代表实际值与输出值之间的差值[5]。
2.2 数据处理
先用一定的样本数据对其进行训练,确定合理的权重和阈值,输入层向隐含层的信息传递如式(4)所示
隐含层第j个神经元输出如式(5)所示:
激励函数如式(6)所示:
只有通过对网络各层次间的权重和阈值进行不断的学习优化,才能得到最理想的输出值。 以神经网络第p 个训练样本为例,其输出误差EP如式(7)所示:
对于整个样本,神经网络总的累计误差可以表示为式(8):式(8)中,P为训练样本总个数。
3 中期电力负荷预测
3.1 时间序列优化算法
式(9)表述t时刻采样点的值会受到前期n个点时刻值的影响,所以将前面n时刻的初始输出值作为输入量代入神经网络分析模型f中,推出t时刻输出值y(t)。 研究人员将表1 中第2 列前3 个值作为表中第1 行输入值X1,X2,X3,第2 列第4 个值作为第1 行输出量Y;将第2 列中第2个值到第4 个值作为第2 行输入值X1,X2,X3,第2 列第5个值作为第2 行输出量Y,以此类推,用来表示每个月总用电量受前3 个月影响[6]。

表1 电力负荷数据统计
3.2 BP 神经网络-时间序列预测模型仿真对比
在本次预测中,研究人员选用了表1 中的Y 值作为样本数据,并采用了BP 神经网络模型进行预测。 选择BP神经网络的原因是它具备出色的非线性建模能力,能够更好地捕捉复杂数据背后的关联关系。 不仅如此,研究人员还引入了气象和节假日两个关键因素作为网络的训练样本。 气象因素包括温度、湿度等气象数据,而节假日因素包括传统节假日、特殊事件等时间相关的信息,这些因素的引入可以提高模型的预测精度。 研究人员的目标是对未来一个月的用电量数据进行预测,并与实际数据进行对比。 见图2、图3、图4。

图2 无影响因子

图3 考虑气象因子
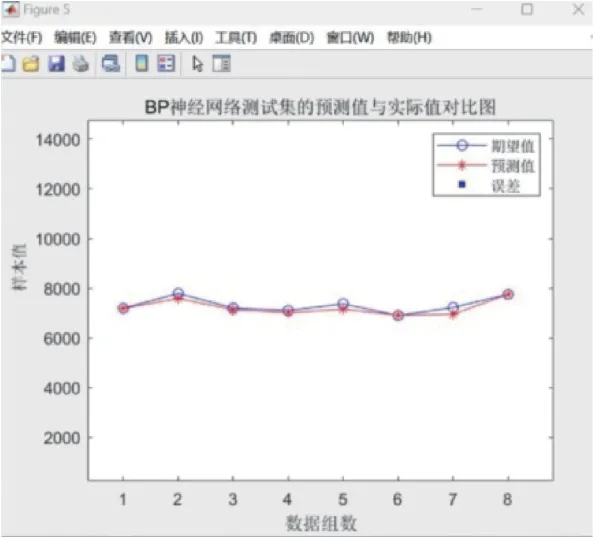
图4 考虑气象、节假日因子

图5 预测一均方误差图
预测一(如图2 所示):在不考虑影响因子的情况下,只根据实际用电负荷进行网络训练。 从图3 中可以看出,实际值与预测值存在较大误差。
预测二(如图3 所示):考虑气象影响因素,由于我国7 月、8 月两个月份受极端天气影响,出现高温和强降水,用电负荷增加,出现周期性波峰。 考虑气象因素后,神经网络自动调节训练值,使结果更加准确。
预测三(如图4 所示):综合考虑气象、节假日两个因素,再次进行自动调节训练,使误差进一步缩小。
3.3 BP 神经网络-时间序列模型在电力负荷中期预测中的表现
本文引入了三组实验数据的均方误差图,即预测一(图5)、预测二(图6)和预测三(图7),其中均方误差(mean square error, MSE)越小表示预测模型的拟合效果越好。首先,让研究人员关注预测一,根据给出的数据,预测一中的均方误差为0.587 6。 此值相对较大,可能数据之间的关联性较弱,考虑是否有其他影响因素未被纳入模型[7-8]。 其次,预测二中的均方误差为0.424 8。 说明模型在预测二的情境下拥有更好的拟合效果,可能是因为在预测二的场景中引入了气象相关因素,使得模型能够更准确地捕捉到电力负荷变化的规律。 最后,预测三中的均方误差为0.013 3。 这个极小的误差表明,在预测三的情境下,模型的拟合效果非常好,在预测二的基础上又加入了节假日因素影响分析,使得预测结果非常接近实际观测值。

图6 预测二均方误差图

图7 预测三均方误差图
综合前文分析可以看出,BP 神经网络-时间序列模型相比于时间序列模型对中期负荷的预测更为准确,尤其是神经网络模型中在引入影响因子后预测结果更加趋近于真实值。
4 结语
本文结合了BP 神经网络和时间序列分析的优化模型有效地弥补了它们各自的不足之处,并且在多个方面表现出色。 首先,该模型适用于处理大规模或小规模的数据集,具备广泛的适用性。 其次,该模型能够出色地捕捉数据的周期性特征,对于分析和预测具有明显周期性变化的数据非常有效。 再次,它具有快速适应性,能够在短时间内应对负荷快速变化,提高了实时性。 最后,经过优化后,该结合模型的预测精度显著提升,提供了更可靠的结果,适用于各种应用场景。 综上所述,本研究具有重要的应用和学术价值,值得相关领域参考和借鉴。

