基于多元线性回归的空气质量指数预测模型
王凯文,李宏滨
(太原师范学院计算机科学与技术学院 山西 晋中 030600)
0 引言
中国是世界上的人口大国,也是世界上最大的制造业和工业生产国之一。 一直以来,空气污染问题的解决面临着严峻考验,尤其是在城市地区,PM10、O3、SO2、PM2.5、N02、CO 等污染物对人体健康和环境的影响非常严重。 建立空气质量指数(air quality index, AQI)与不同污染物浓度之间的模型有多重意义。 首先,AQI 是一个用于评估空气质量的标准化指数,建立AQI 与不同污染物浓度之间的模型可以帮助政府相关部门准确地评估空气质量,从而采取更有效的措施保护公众健康。 其次,AQI 与不同污染物浓度之间的模型可以帮助政策制定者了解不同污染物的影响程度,从而制定相应的环境政策。 最后,AQI 是一个国际标准化指数,可以用来比较不同地区的空气质量,与不同污染物浓度之间的模型可以帮助不同地区使用相同的指数来评估和比较空气质量,从而更好地了解不同地区的环境状况。 因此,建立AQI 与不同污染物浓度[1]之间的模型对于环境保护和公众健康有着重要的意义。
1 相关概念
1.1 AQI
AQI[2]是一项关键的环境指标,旨在向公众传递有关空气质量状况的信息。 该指数在计算过程中综合考虑了颗粒物(PM10和PM2.5)、臭氧(O3)、二氧化硫(SO2)、一氧化碳(CO)、氮氧化物(NO2)等多种空气污染物[3]。 AQI的计算方式也由于地区的不同存在一定的差异,计算结果按照不同的数值范围进行划分,不同范围代表空气质量的不同等级,例如:0~50 代表当前地区的空气质量为优等。
1.2 皮尔逊相关系数
皮尔逊相关系数(Pearson correlation coefficient)是一种用来计算两组变量之间线性关系强弱和方向的量。 在具体应用过程中通常使用字母“r” 表示,它的取值范围是[-1,1]。 r 的计算结果为1 时代表完全正相关;r 的计算结果为-1 时表示完全负相关。 r =0 表示无相关性:两个变量之间没有线性关系。
皮尔逊相关系数的值不仅表示线性关系的强度,还可以用来表明两组变量关系的方向。 呈正相关时,其值为正;呈负相关时,其值为负。
1.3 多元线性回归模型
多元线性回归是一种统计模型,用于建立多个自变量与一个因变量之间的关系。 这个模型可以用于预测和解释变量之间的复杂关系。 多元线性回归的目标是找到合适的回归系数,使得模型对观测数据的预测误差最小化。这通常通过最小二乘法来实现,即通过最小化观测值与模型预测值之间的残差平方和。
建立多元线性回归模型的主要步骤包括数据收集、变量选择、模型拟合、模型评估和预测。 多元线性回归模型的解释性较强,能够同时考虑多个自变量对因变量的影响。 与此同时,该模型也存在一些缺点,例如,模型的有效性依赖于一些假设,如误差项的正态性和方差齐性。 在应用中,还需要注意避免过拟合(模型过度复杂,对训练数据过于敏感)。
2 问题分析
首先,模型的建立需要通过《中国统计年鉴2022》完成对某城市全年空气污染物浓度数据的采集,同时对采集到的数据进行统计分析,对数据异常值、缺失值进行预处理工作;其次,通过建立相关性分析模型,计算AQI 与这些污染物之间相关性的强弱[4],并根据污染物在空气中的浓度值、影响范围以及对人体是否有害等因素,确定对空气质量有影响的污染物主要有六种;最后,将六种污染物浓度作为自变量,AQI 作为因变量,建立多元线性回归模型,根据模型预测的AQI 与真实AQI 进行比较,确定该模型的实用性和精确度。
3 数据处理
本文主要探究AQI 与各污染物浓度之间的数学模型,因此不受城市变化的影响。 从中挑选了某城市2022年的空气质量指数与空气污染物浓度的数值。 数据的内容如表1 所示。
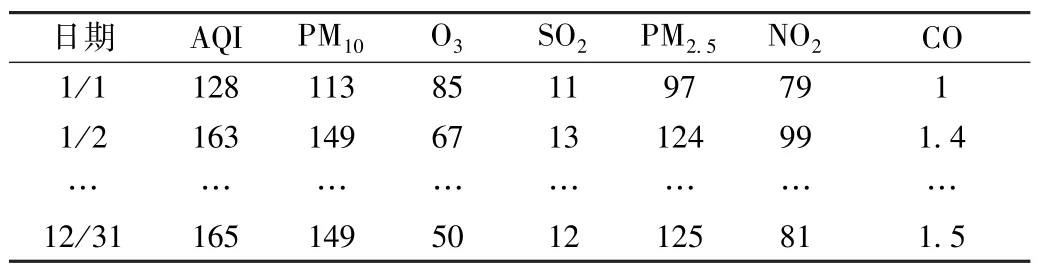
表1 2022 年某城市AQI 与空气污染物浓度数据
3.1 缺失值处理
在对数据进行统计分析时发现数据是不连续的,为了满足时间序列本身是连续、平滑的特性,对数据中的缺失值进行填充。 常用的缺失值填充方法有随机填补法、均值法、中位数法、众数法等。 此外,K-最近邻(K-nearest neighbor, KNN)、回归预测、期望最大化(expectation maximization, EM)等建模方法也可用来进行数据填充。由于数据集缺失值比重低,且构成的时间序列的周期长,因此采用对应污染物的平均浓度限值作为缺失数据进行填充。
3.2 数据有效性处理
首先,确定CO 数据允许保留三位小数,其他污染物的数据允许保留两位小数;其次,对数据进行更详细的判断:将值按小数点进行分割,如果分割后的部分不是两部分,或者小数部分的长度超过3 位,则数据无效;最后,对于无效的数据也采用对应污染物的平均浓度限值进行修改。
4 模型建立
4.1 相关性检验
从《中国统计年鉴2022》以及某些地方政府网站发布的监测得知,我国空气污染物主要的监测指标主要有六项,分别是PM10(粗颗粒物)、PM2.5(细颗粒物)、SO2、NO2、CO 和O3。 AQI 是用来评价空气质量情况的无量纲相对数值。
设空气质量指数为因变量Y,各污染物浓度为Xi(i =1,2,3,…,n) ,其中n为对AQI 有影响的污染物种类数。通过使用皮尔逊相关系数进行相关性分析[3],分析空气质量指数与各污染物浓度之间的相关性。 具体的步骤如下所示:
以AQI 与NO2之间的相关性计算[4]为例,假设AQI的样本数据为Y:{Y1,Y2,Y3,…,Yn} ,污染物NO2浓度的样本数据为X:{X1,X2,X3,…,Xn}。
步骤1:用公式(1)、(2)计算样本均值:
步骤2:用公式(3)、(4)计算样本的标准差:
步骤3:用公式(5)计算样本的协方差:
步骤4:用公式(6)计算皮尔逊相关系数:
其中,相关系数r的数值越趋近于1 或-1,相关性越强;趋近于0 时,相关性越弱。 通过上述求解,可以得出AQI 与各个污染物浓度之间的相关系数,如表2 所示。 对各相关系数进行分析,确定收集数据中的六项指标都与空气质量指数有较强的相关性。

表2 AQI 与各污染物浓度相关系数
4.2 多元线性回归模型建立
4.2.1 转化分指数
因为不同污染物的浓度单位和浓度范围不同,直接使用浓度值来计算AQI 可能会出现不公平或不准确的情况,所以将空气污染物的浓度转化为分指数可以更准确地评价空气质量,反应不同污染物对人体健康和环境的影响程度,避免了不公平或不准确的情况。
同时,分指数的计算也考虑了不同级别的污染物标准限值,以及不同污染物的影响程度,可以更加客观地评价空气质量,避免了过度关注某一种污染物而忽略其他污染物对空气质量的影响。 各污染物浓度区间值如表3 所示。

表3 污染物浓度区间值
分指数计算公式如式(7)所示。
转化后AQI 部分数据的分指数如表4 所示。
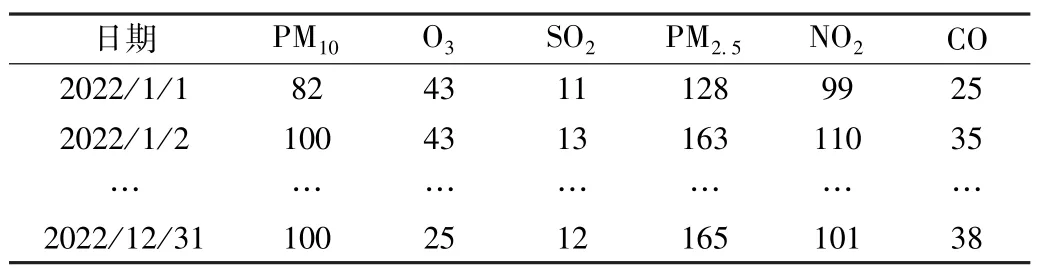
表4 转化后AQI 部分数据的分指数
4.2.2 多元线性回归模型
假设上述处理过的数据为D,一条样本数据中有d条影响AQI 的空气污染物属性指标。 通过多元线性回归模型[5-6],最终目标是寻找d维列向量ω与常数b,使模型为式(8)所示。
目的是使预测值尽可能接近真实值yi。 使用Python中的Numpy、Pandas 等库对上述模型进行求解,得到各个指标分量的系数ω以及偏移量b[7],进而得到空气质量指数与各污染物浓度的关系表达式如式(9)所示。
将数据中的各污染物浓度数值分别代入上述公式,计算出每天空气质量指数的预测值y^。
5 结果分析
使用上述建立的AQI 与不同污染物浓度之间的数学模型[8],对该城市AQI 进行计算得到预测值,并与真实值进行比较,其部分结果如表5 所示。

表5 AQI 预测值与真实值对比
最后,通过皮尔逊相关系数计算真实值与预测值的相关性,计算结果为0.928。 经过验证,上述函数y =-1.134x1+0.793x2+0.729x3+1.287x4+0.100x5+0.387x6+4.104 预测结果较为准确。
6 结语
首先,本文对收集到的各空气污染物浓度进行统计分析,使用各污染物的平均浓度限值对缺失数据进行填充;其次,将空气污染物浓度转化为分指数,解决了直接使用浓度值来计算空气质量指数可能会出现不公平或不准确的情况;最后,使用多元线性回归对问题进行建模,最终得到的模型可以将多种污染物的浓度综合考虑,AQI 预测准确率达到了0.928,能够反映空气质量的总状况。 但是,该模型并没有考虑季节等相关因素的影响,因此可以考虑将各城市每年的数据按照季节[9]进行划分,分别进行构建AQI 与各影响指标之间的关系模型,进一步提高模型的精确率。

