基于自适应多保真度Co-Kriging 代理模型的地下水污染源反演识别

安永凯,张岩祥,闫雪嫚(1.长安大学水利与环境学院,陕西 西安 710054；2.长安大学旱区地下水文与生态效应教育部重点实验室,陕西 西安 710054；.中国电建集团西北勘测设计研究院有限公司,陕西 西安 710065；4.西北大学城市与环境学院,陕西 西安 710127)

地下水污染具有存在的隐蔽性和发现的滞后性等特点,致使人们难以直接了解和掌握地下水污染的相关状况(如污染源的空间位置和释放历史),这对地下水污染修复方案合理制定、风险评估以及责任认定带来极大的困难[1-2].地下水污染源反演识别能够根据污染场地地下水水位和污染质浓度监测数据,结合现场调查、动态试验、专业知识和专家经验等辅助信息,对描述地下水污染的数值模拟模型进行反演求解,从而识别确定含水层中污染源个数、位置和释放历史等地下水污染源参数[3-4].

现有地下水污染源反演识别方法主要可分为以下几类:解析法、直接法、模拟优化法以及随机统计法[5-6].其中,模拟优化法是地下水污染源反演识别研究中应用最广泛的方法[7-8].但模拟优化法只能给出污染源参数的“最优解”,无法充分描述其不确定性[9].与模拟优化法不同,应用随机统计法开展地下水污染源反演识别研究可获得未知污染源参数的后验分布,不仅可充分描述其不确定性,且所得到的信息量更大从而能够为地下水污染修复治理、风险评估等提供更多的参考信息[10-11].然而,应用随机统计法进行地下水污染源反演识别需成千上万次地运行地下水溶质运移数值模拟模型,由此产生了庞大的计算负荷及冗长的计算时间[10].建立模拟模型的代理模型是解决该问题的有效途径[12-13].

代理模型可以用非常低的计算代价对复杂模拟模型的输入输出关系进行近似代理[14],根据其构建方式,代理模型可分为两大类:第一类是响应面代理模型,第二类是多保真度(MF)代理模型[15].前者是仅利用高保真度(HF)模型(即原始模拟模型)输入输出样本构造的数据驱动代理模型,具有易于实施的优点,在水文地质领域得到了广泛应用[2,16].HF 模型精度高但计算成本也高,导致第一类代理模型的构建仍需昂贵的计算成本,因此学者们提出综合运用HF模型信息和低保真度(LF)模型信息来构建MF代理模型.其中,LF 模型可通过离散网格粗化、模型降阶等简化方式得到,相比于HF 模型,LF 模型精度较差但计算成本也低,可以提供充足的样本[17].MF 代理模型旨在通过MF 模拟框架充分挖掘HF 模型和LF 模型之间的相关关系,进而用少量HF 模型样本和大量LF 模型样本构建兼顾HF 模型精度与LF 模型效率的代理模型[18].相比于常用的响应面代理模型,MF 代理模型能够进一步提高计算效率且对模拟模型的逼近精度更高[19-20].但在地下水污染源反演识别研究中,MF 代理模型却鲜有报道.同时,采用自适应更新多保真度代理模型策略,即将每一轮地下水污染源反演识别结果带入HF 模型,获得新的训练样本,进而重新构建MF 代理模型,可以有效进一步提升MF 代理模型对模拟模型的逼近精度,以此重新进行地下水污染源反演识别,能够极大地提高地下水污染源反演识别精度.

基于此,本文研究应用集成差分进化算法的Co-Kriging 方法建立地下水数值模拟模型的MF 代理模型,在此基础上,耦合多保真度Co-Kriging 代理模型和MCMC-DREAM(D)算法,并采用自适应更新多保真度代理模型策略进行地下水污染源反演识别,旨在为地下水污染修复治理提供参考.

1 研究方法

技术路线如图1 所示.

图1 技术路线Fig.1 Technology roadmap

1.1 Co-Kriging 代理模型

Co-Kriging 代理模型是Kriging 代理模型的一种扩展性形式,由两组互不干扰的高、低保真度样本共同构建而成的MF 代理模型[21].相比于只用高保真度样本建立的Kriging 代理模型,Co-Kriging 代理模型在保持非常高的代理精度的同时,能够有效降低获取高保真度样本所需的时间和计算代价[22].

假设有两组高、低保真度样本,分别为{Xh,Yh}和{Xl,Yl}, 其中Xh和Xl为样本输入,且Xh⊆Xl, Yh和 Yl为样本输出.这些样本集合起来表示如下:

式中:nh和nl分别为高、低保真度样本数量.

使用Zh和Zl分别表示高、低保真度样本的高斯过程,两者之间的关系可以使用式(3)表示:

式中:ρ为缩放因子,Zd表示Zh与ρZl之间差异的高斯过程.

参照 Kriging 代理模型中协方差矩阵的结构,Co-Kriging 代理模型的完整协方差结构如式(4)所示[23]:

式中:ψl和ψd为相关矩阵,和可以参照Kriging代理模型求解.

协方差矩阵C中有5个超参数需要优化,分别为θl、θd、pl、pd和ρ.可以使用极大似然估计(Maximum Likelihood Estimate, MLE)获取上述超参数.

通过使式(5)取得最大值求得θl和pl:

通过使式(6)取得最大值求得θd、pd和ρ:

在获得超参数之后,可以使用式(7)预测任意一点在高保真度的高斯过程中的响应值.

1.2 差分进化算法

上述Co-Kriging 代理模型的超参数往往需要配合优化算法方可求得,优化算法—差分进化算法(DE).DE 是一种高效的全局优化算法,与遗传算法的进化流程非常相似,都包括变异、交叉和选择操作,但这些操作具体定义与遗传算法有所不同[24].如图2 所示,DE 的进化流程如下:(1)确定适应度函数、种群大小、缩放因子、交叉概率和进化代数.(2)随机产生初始种群.(3)计算初始种群的适应度值.(4)对初始种群进行变异和交叉,得到中间种群.(5)计算中间种群的适应度值.(6)在初始种群和中间种群中选择个体,更新初始种群.(7)判断是否达到终止条件或最大进化代数,若是,则终止,若否,转步骤(4).

图2 差分进化算法的进化流程Fig.2 Process of differential evolution algorithm

1.3 贝叶斯推理

贝叶斯推理源于贝叶斯理论.贝叶斯公式是贝叶斯推理的数学表达,用于表达先验分布和后验分布的关系,目前贝叶斯推理被广泛应用于模型参数识别及不确定性分析[25].贝叶斯公式根据先验知识设置参数的初始分布,通过分析样本的概率后,得到参数的后验分布[26],如式(8)所示:

在实际应用中,除了极个别特别简单的模型可以通过解析解推断参数的后验分布,对于绝大多数的复杂模型,只能通过采样的方式获取参数的后验分布[27-28].马尔科夫链蒙特卡洛(MCMC)能够从后验分布采样并进行统计分析,从而得到后验分布的统计特征[29-30].目前,MCMC 方法已经开发出了众多采样算法.其中,DREAM(D)是在DREAM算法的基础上改进而来的,与原始DREAM 算法不同的是,它在处理连续型变量的同时能够有效处理离散型变量,并且能够保持细致的平衡性和遍历性[31].

然后进行马尔科夫链进化:

(2)对于第i(i=1,2, …,N)条马尔科夫链,产生候选种群的公式(9)如下所示:

(3)定义CR(0 ≤CR ≤ 1)为进行子空间演化的交叉概率,进而决定候选种群是否取代初始种群:

式中:U 为随机数,从均匀分布 U( 0,1)采样得到.

(4)计算似然度 p( zi),并进而计算接受率α(θi, zi):

根据接受率 α(θi,zi)的计算结果,判断是否接受zi.

(5)应用Gelman-Rubin 收敛诊断方法[32]判断收敛性,计算收敛性判断指标R:

式中:g 为DREAM(D)算法中的马尔科夫链长度;q 为MC 数目;B 表示q 条马尔科夫链平均值的方差;W 为q 条马尔科夫链内方差的平均值.若R≤12,则认为采样过程已收敛,结束计算,统计分析待求变量θ的后验分布;否则重复步骤.

2 数值试验

2.1 数值算例概述

本文针对2 个数值算例开展研究.算例1:考虑一个二维均质各向同性承压含水层,该含水层东西长为300L,南北宽为240L,东、西两侧边界(Γ1和Γ3)均为线性变化的定水头边界,南、北边界(Γ2和Γ4)均为零通量边界,如图3(a)所示.算例2:考虑一个二维非均质各向同性承压水层,该含水层划分为3 个参数分区,仅对渗透系数进行分区,东西长为300L,南北宽为200L,西北、东南边界(Γ1和Γ3)均为定水头边界,其余(Γ2和Γ4)均为零通量边界,如图3(b)所示.2 个算例的模拟期均为900T,模拟区内有1 个地下水污染源,3 个地下水污染观测井.

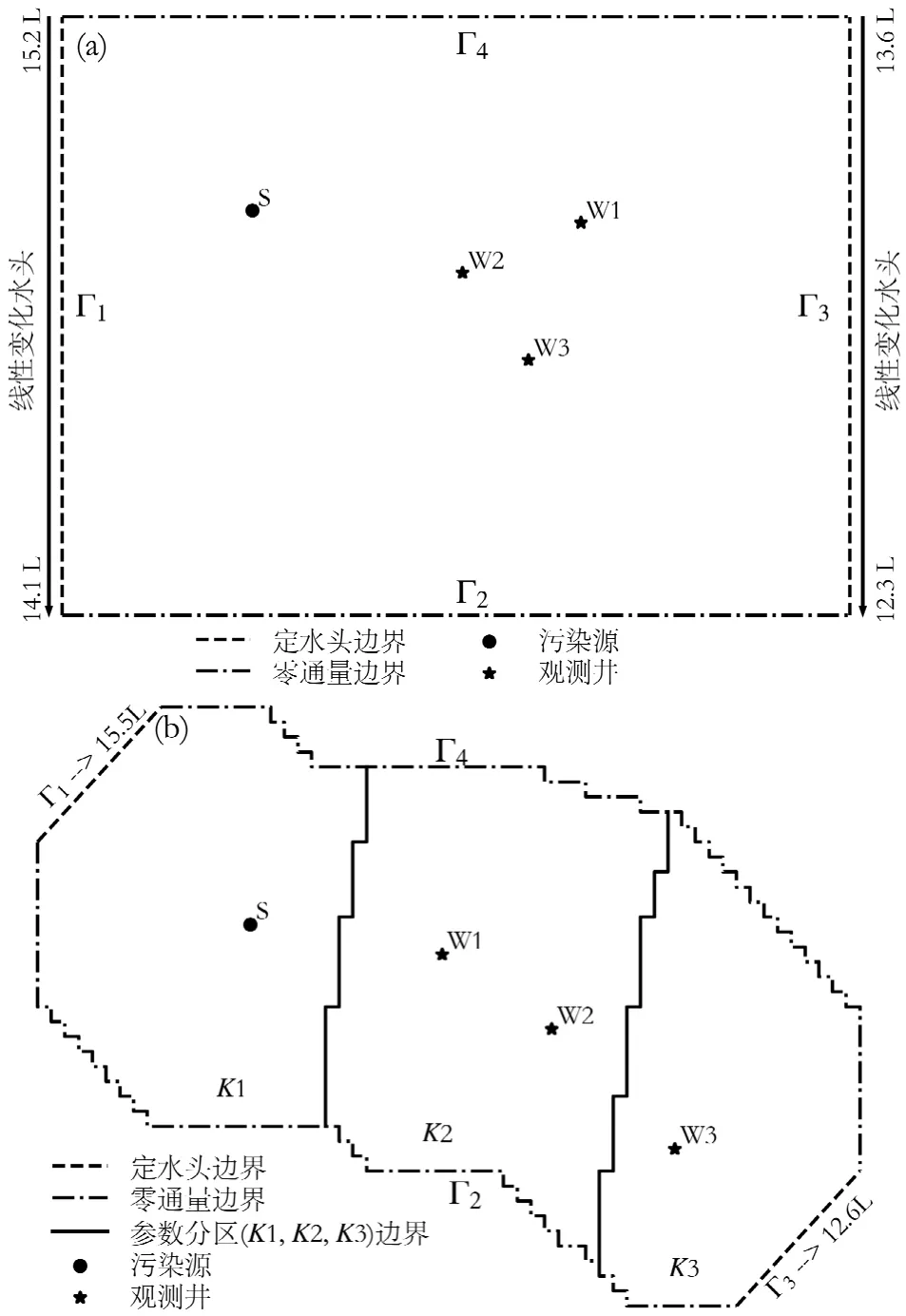
图3 算例含水层平面示意Fig.3 Aquifer plan schematic diagram

本研究假设污染物不会发生化学反应和生物降解作用.算例1:假设污染源初始释放时间(τ)和释放强度(q)未知,并作为待识别变量,渗透系数(K)、纵向弥散度(D)、横向弥散度与纵向弥散度比值(α)和孔隙度(n)等水文地质参数均质且已知,待识别变量先验分布和水文地质参数取值如表1 所示.算例2:假设污染源初始释放时间(τ)、释放强度(q)、3 个分区渗透系数(K1,K2,K3)和纵向弥散度(D)未知,并作为待识别变量,横向弥散度与纵向弥散度比值(α)和孔隙度(n)等水文地质参数已知,待识别变量先验分布和水文地质参数取值如表2 所示.

表1 算例1 待识别变量先验分布和水文地质参数值Table 1 Prior distribution of unknown variables and hydrogeological parameter values for case 1

表2 算例2 待识别变量先验分布和水文地质参数值Table 2 Prior distribution of unknown variables and hydrogeological parameter values for case 2

根据上述设定的水文地质条件,模拟区地下水流运动数学模型如式(13)所示:

式中:H 为地下水水头[L];K 为渗透系数[L/T];M 为含水层厚度[L];S 为贮水系数[-];H0和H1为已知函数[L];Γ1、Γ3为第一类边界条件; Γ2、Γ4为第二类边界条件.为边界上某点外法线方向上的单位向量.

模拟区地下水溶质运移数学模型如式(14)所示:

式中:c 为污染质浓度[ M / L3];Dxx和Dyy分别为x、y方向上的水动力弥散系数[ L2/ T ];ux和uy分别为x、y 方向上的实际平均水流速度[ L / T ];f 为源汇项[ M /( L3T )];c0为已知浓度函数[ M / L3];c1为已知对流-弥散通量函数[ M /(L2T )];Γ1、Γ3为第三类边界条件; Γ2、Γ4为第二类边界条件.

分别对模拟区进行精细离散和粗化离散,建立HF 模型和LF 模型,然后应用MODFLOW 和MT3D分别求解HF 模型和LF 模型.其中,算例1 的HF 模型将模拟区剖分为 800000 个网格(长 1000×宽800),LF 模型将模拟区剖分为2880 个网格(长60×宽48);算例2 的HF 模型将模拟区剖分为375000 个网格(长750×宽500),LF 模型将模拟区剖分为2400 个网格(长60×宽40).

2.2 Co-Kriging 代理模型的建立

本文算例1 待反演识别变量包括污染源初始释放时间(τ)和释放强度(q),相应的代理模型输入则为上述的2 个待识别变量,输出为3 口监测井在3 个时刻(t=780T ,840T ,900T )监测到的污染物浓度值,共9 个变量;算例2 待反演识别变量包括污染源初始释放时间(τ)、释放强度(q)、3 个分区渗透系数(K 1, K 2, K 3)和纵向弥散度(D),相应的代理模型输入则为上述的6 个待求变量,输出为3 口监测井在3个时刻(t=780T ,840T ,900T )监测到的污染物浓度值,共9 个变量.

Co-Kriging 代理模型的构建步骤如下:首先,采用拉丁超立方抽样方法在待识别变量的先验分布内分别抽取5 个和200 个训练样本,将抽取的5 个训练样本代入精细离散的HF 模型,同时将抽取的200个训练样本代入粗化离散的LF 模型;然后,运转HF模型和LF 模型,分别得到对应的模型输出;接下来,基于5 组HF 模型输入-输出样本构建Kriging 代理模型,基于5 组HF 模型和200 组LF 模型输入-输出样本构建Co-Kriging 代理模型,即MF 代理模型;最后,重新采用拉丁超立方抽样方法在待识别变量的先验分布内抽取 5 个检验样本,将其分别代入Kriging 模型和MF 代理模型,运转模型,得到相应的模型输出,并将它们与HF 模型的输出结果进行对比分析,从而评估Kriging 代理模型和MF 代理模型的精度.整体的MF 代理模型构建流程如图4 所示.

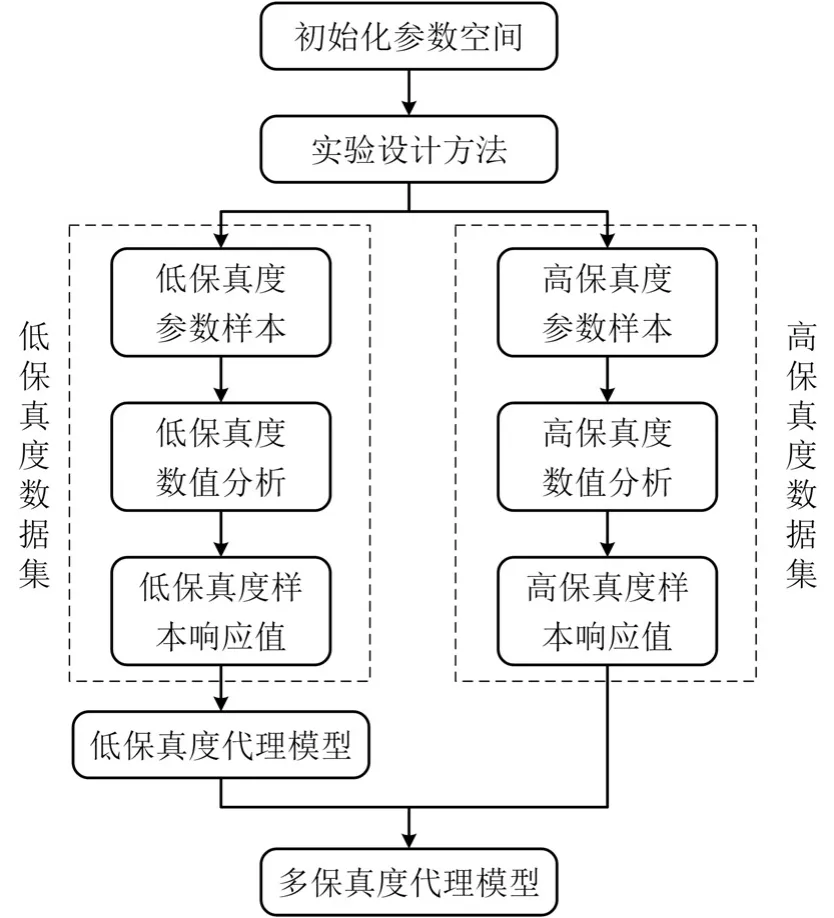
图4 Co-Kriging 代理模型的构建流程[18]Fig.4 Construction process of Co-Kriging surrogate model[18]

由图5 可以看出,MF 代理模型平均相对误差均小于Kriging 代理模型,这说明对于相同的输入,MF 代理模型对HF 模型的逼近精度更高,MF 代理模型比Kriging 代理模型更适合后续地下水污染源反演识别.

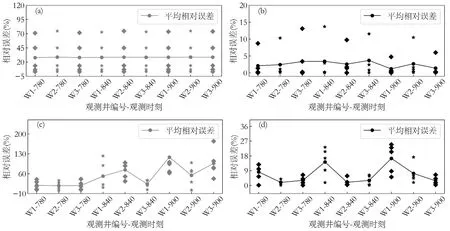
图5 Kriging 代理模型与MF 代理模型精度Fig.5 Accuracy of Kriging surrogate model and MF surrogate model

对于算例1,HF 模型和MF 模型单次运行时间分别为1964.747s 和0.016s;对于算例2,HF 模型和MF 模型单次运行时间分别为2013.366s 和0.018s.HF 模型单次运行时间较长,在地下水污染源反演识别过程中成千上万次调用HF 模型,需要数月才能识别完毕,因此,不合适用于地下水污染源反演识别;MF 代理模型单次运行时间十分短,在地下水污染源反演识别过程中需要成千上万次调用MF 模型,仅需数分钟便能识别完毕,且对HF 模型的逼近精度很高,十分适合用于地下水污染源反演识别.使用MF 代理模型进行地下水污染源反演还需要考虑构建MF 代理模型的时间,构建MF 代理模型时间花费主要来自运行HF 模型,在本研究中需要运行5 次HF 模型,需要数小时便能完成.总而言之,在地下水污染源反演识别过程中直接调用MF 代理模型所需时间远远小于调用HF 模型,更适合用于地下水污染源反演识别.

2.3 污染源反演识别

在构建Co-Kriging 代理模型的基础上,研究应用DREAM(D)算法分别对两个算例的待识别变量进行反演识别.为保证待识别变量均收敛于稳定的后验分布采样过程的收敛性,本文采用Gelman-Rubin收敛诊断方法对DREAM(D)算法采样过程的收敛性进行检验.对于算例1,DREAM(D)算法的采样过程如图6(a)和图6(b)所示.污染源初始释放时间(τ)和释放强度(q)这2个待识别变量均能收敛于稳定的后验分布.对于算例2,DREAM(D)算法的采样过程如图7(a)、(b)、(e)、(f)、(i)、(j)所示.污染源初始释放时间(τ)、释放强度(q)、3 个分区渗透系数(K 1, K 2, K 3)、和纵向弥散度(D)这6 个待识别变量均能收敛于稳定的后验分布.

图6 算例1 待识别变量的采样迭代过程及其反演识别结果Fig.6 Sampling iteration process and identification results of unknown variables for case 1

在确保采样过程收敛性后,算例1 选取后1000组样本进行统计分析,获得2 个待识别变量的反演识别结果;包括其后验分布及统计特征值.算例2 选取后10000 组样本进行统计分析,获得6 个待求变量的反演识别结果,包括其后验分布及统计特征值.

由图6 和图7 可知,待识别变量后验分布均存在明显的峰值,这说明DREAM(D)算法能够实现对待求变量的有效反演识别.此外,可以明显看出,算例1的2 个待识别变量的真实值均落在其后验分布的高密度区域;同时,待识别变量后验分布的最大后验概率(MAP)值与其真实值很接近.这说明,DREAM(D)算法能够得到较高精度的反演识别结果.算例2 的污染源初始释放时间(τ)和 3 个分区渗透系数(K 1, K 2, K 3)这4 个待识别变量的真实值均落在其后验分布的高密度区域;同时,待识别变量的后验分布的MAP 值与其真实值很接近,这说明,DREAM(D)算法对这4 个变量得到良好识别.污染源释放强度(q)和纵向弥散度(D)这4 个待识别变量的真实值落在其后验分布的低密度区域,这2 个变量未能得到良好识别.

图7 算例2 待识别变量的采样迭代过程及其反演识别结果Fig.7 Sampling iteration process and identification results of unknown variables for case 2

为了进一步提高污染源反演识别精度,采用自适应更新多保真度代理模型策略,即将上一轮污染源反演结果后验分布的MAP 值代入HF 模型,获得新的输入-输出训练样本,训练新的多保真度Co-Kriging 模型,进而进行下一轮污染源反演识别.分别对算例1 和算例2 进行2 次和3 次自适应更新,待识别变量反演结果如图8 和图9 所示.

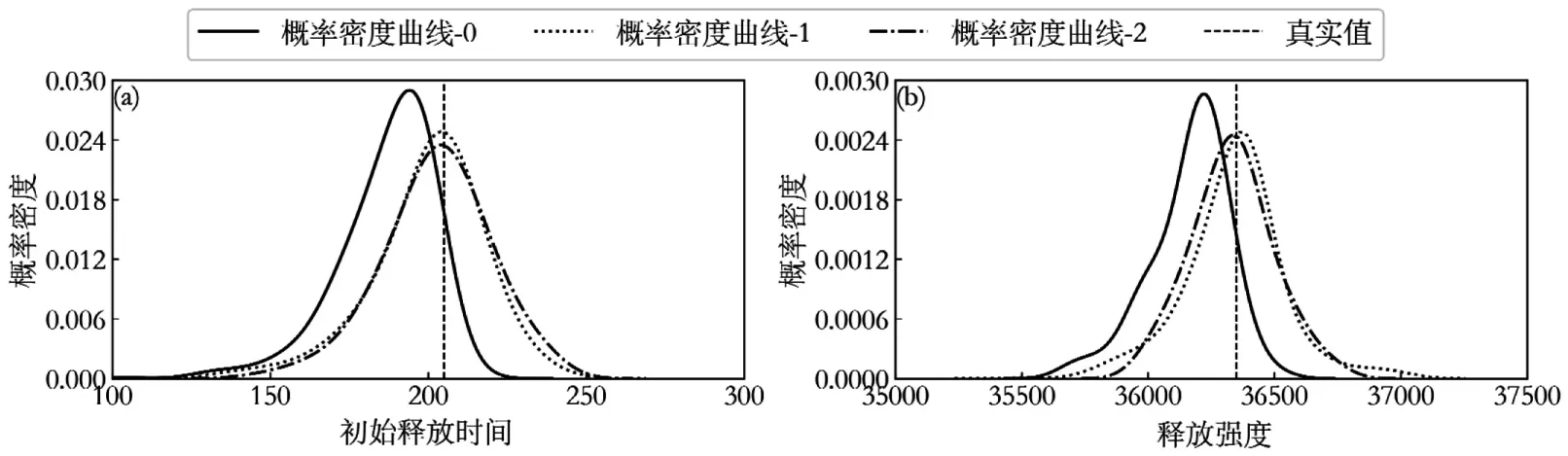
图8 算例1 待识别变量反演识别结果Fig.8 Identification results of unknown variables for case 1

概率密度曲线的MAP 值越靠近真实值,说明反演识别结果越好.由图8 可以看出,经过1 次自适应更新后,待识别变量的MAP 值与其真实值更加接近,表明自适应更新策略能够显著提升污染源反演精度.经过2 次自适应更新后的污染源反演结果与经过1 次自适应更新后基本一样,没有显著差别,表明自适应更新策略有助于得到高精度且稳定的污染源反演结果.由图9可以看出,经过3次自适应更新后,污染源释放强度(q)、渗透系数(K2)和纵向弥散度(D)的MAP值与其真实值更加接近,表明自适应更新策略能够显著提升反演精度.渗透系数(K1,K2)的MAP 值与更新前无明显差别,初始释放时间(τ)的MAP 值稍微远离其真实值,表明自适应更新策略未能够提升反演精度,原因在于模型输出值(污染物浓度)对初始释放时间(τ)不敏感和DREAM(D)算法进行参数识别本身存在一定随机性,故而难以提升反演识别精度.综合算例1和算例2,采用自适应更新多保真度代理模型策略能够进一步提升污染源反演识别精度.

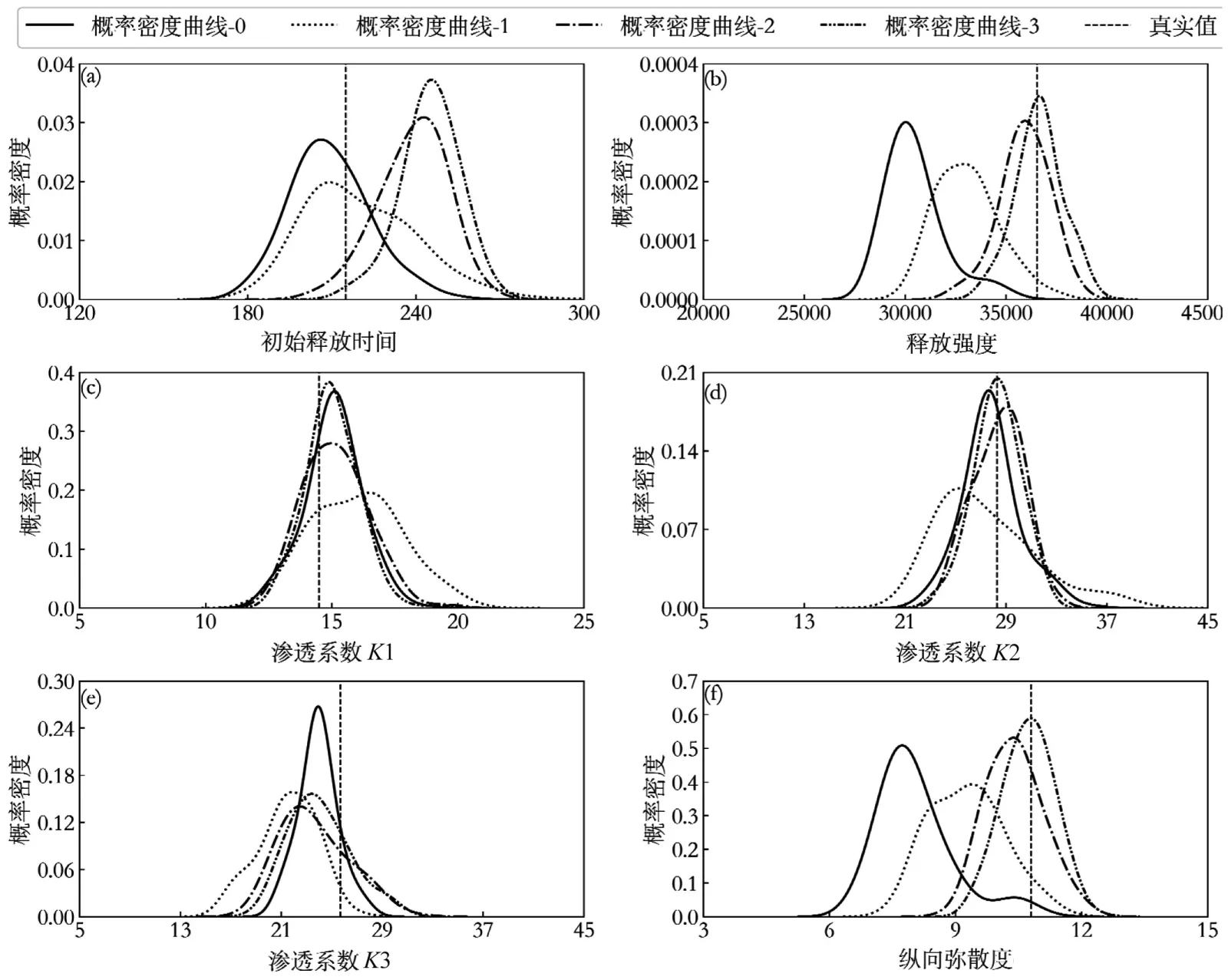
图9 算例2 待识别变量反演识别结果Fig.9 Identification results of unknown variables for case 2

因此,基于Co-Kriging 代理模型和DREAM(D)算法的地下水污染源反演识别是可行有效的.然而,本文构建的Co-Kriging 代理模型只适合于当前水文地质条件和模型时空离散,当水文地质条件和模型时空离散变化时,需要重新构建Co-Kriging 代理模型.

3 结论

3.1 相比仅基于高保真度模型输入-输出样本构建的Kriging 代理模型,联合运用高保真度和低保真度模型输入-输出样本构建的Co-Kriging 代理模型对模拟模型的逼近精度更高.

3.2 耦合多保真度 Co-Kriging 代理模型和MCMC-DREAM(D)算法能够得到较高精度的污染源反演结果,且能够大幅度减小计算负荷;同时,采用自适应更新多保真度代理模型策略能够进一步提升污染源反演识别精度.