基于联合GLMB滤波器的可分辨群目标跟踪

齐美彬, 庄 硕,*, 胡晶晶, 杨艳芳, 胡元奎

(1. 合肥工业大学计算机与信息学院, 安徽 合肥 230009; 2. 合肥工业大学物理学院,安徽 合肥 230009; 3. 中国电子科技集团第38研究所, 安徽 合肥 230088)

0 引 言

在雷达领域,多目标跟踪是指跟踪区域显示多条目标轨迹,通常假设目标为点目标。而随着新型传感器技术的发展,高分辨率雷达、远程探测雷达等传感器能收集到更加丰富的目标信息,传感器可以从一个目标中获得多个量测值,称为扩展目标。同时,高分辨率雷达可以分辨多个目标聚集运动的目标,也就是多个目标之间距离相近,形成了一个运动状态相同的编队,称之为群目标。当群目标的量测位于传感器的不同分辨率单元时,群内成员之间能较好分离,传感器可以获取每个目标成员的运动信息,称为可分辨群目标。

扩展目标和群目标分别针对单个目标和多个独立子目标产生量测值,但是在运动模型、状态估计和形状估计等方面具有相似性,例如都具有特定的形状并且产生多个量测值;其次,量测点之间的距离较近,这使得传统数据关联算法[1-4]难以实现跟踪。群内目标的运动受到其他成员的影响,在运动过程中还会存在目标分离、合并等情况,导致群内目标数量的不确定性较大,随机有限集(random finite sets, RFS)[5-6]方法可以处理时变目标数,为群目标跟踪问题提供可行的解决方案。为便于描述,本文对扩展目标与群目标不作区分,将目标统称为群目标。

2007年,Mahler[7]基于RFS框架提出了群目标跟踪算法,该算法将概率假设密度(probability hypothesis density, PHD)滤波器应用于扩展目标,可以同时估计目标状态和个数,实现扩展目标PHD(extend target PHD, ET-PHD),并且文献[8]在扩展多目标中应用了势PHD(cardinality PHD, CPHD)滤波器。2015年,文献[9]将广义标签多伯努利(generalized labeled multi-Bernoulli, GLMB)滤波算法引入多扩展目标估计目标状态,但是该算法没有估计群结构问题。文献[10]将图理论与蒙特卡罗方法结合,提出群演化模型估计群目标结构与状态,该方法局限于目标为个数的场景。随后,文献[11]结合图理论,引入邻接矩阵建立动态群模型,并在给定群动态模型的基础上采用GLMB算法,推导出目标估计状态和目标数目,最后利用邻接矩阵估计群结构和子群个数。文献[12]构建了群结构连接信息并将其用于估计协作噪声方差和校正目标预测状态。文献[13]针对可分辨群目标引入了群目标模型,来描述群内目标之间的依赖关系,并且采用Gibbs-GLMB滤波器[14-17]进行状态估计。

超图是图的一种推广,能够表示顶点之间的关系。在计算机视觉、模式识别以及机器学习等领域,超图匹配[18-19](hypergraph matching, HGM)被广泛用于特征点的匹配。近年来,HGM被引入群目标跟踪领域,文献[20]在超图理论的框架下描述群结构,将传统的多目标跟踪(multiple target tracking, MTT)数据关联问题表述为轨迹与量测生成的超图之间的匹配问题,提升显式数据关联的性能。文献[21]在高斯混合实现的标签多伯努利(labeled multi-Bernoulli, LMB)滤波中引入HGM方法,将目标间的位置建模为超图,以提升滤波过程的数据关联性能。

受此启发,本文在联合GLMB(joint GLMB, J-GLMB)滤波器的基础上,结合图论和HGM研究可分辨群目标跟踪算法。由于J-GLMB滤波基于量测与预测状态的关联概率来生成高斯假设的权重,为提升假设中量测-预测状态的关联性能,引入HGM方法将量测-预测表示为两个超图,进而求解点对点的匹配问题。本文提出的算法首先采用改进的J-GLMB滤波器估计目标状态和数目,其次通过图理论估计可分辨群目标结构与子群数目,并通过邻接矩阵估计协作噪声,以此来校正目标的预测状态;最后通过线性仿真实验证明所提改进算法在跟踪精度和子群数目估计方面均优于原始滤波算法。

1 群目标运动模型

群目标由多个目标组成,同一组群目标内的目标保持一定的依赖结构进行运动,包含父节点目标和子节点目标,子节点目标运动受到父节点目标的影响,而父节点目标的运动不依赖于任何目标[22]。因此,对于群内的每个可分辨群目标,当目标只拥有一个父节点时,可以将运动模型建模为

xk+1,i=Fk,lxk,l+bk(l,i)+Γk,iωk,i

(1)

zk+1,i=Hk+1xk+1,i+vk+1,i

(2)

式中:xk+1,i表示目标i在k+1时刻的运动状态;zk+1,i表示目标i在k+1时刻的量测状态;Fk,l和Hk+1分别表示线性系统的状态转移矩阵和观测矩阵;Γk,i表示状态噪声系数矩阵;ωk,i和vk+1,i分别表示过程噪声与量测噪声;bk(l,i)表示目标l与目标i之间的偏移矢量,目标l是目标i的父节点。

当一个目标具有多个父节点时,目标运动会受到父节点的影响,线性系统的运动模型为

(3)

(4)

式中:ωk(l,i)表示加权系数;偏移向量bk(l,i)包含了父节点l与其子节点i之间的位置偏移和方向偏移;P(i)表示目标i的所有父节点;ωk,i～N(0,Qk,i),Qk,i表示过程噪声协方差矩阵。

假设所有目标具有相同的转移状态,即Fk,l=Fk,式(3)可以简写为

xk+1,i=Fkxk,i+Δbk(l,i)+Γk,iωk,i

(5)

(6)

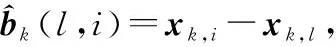
(7)

本文假设群目标做简单运动[12],并且位移向量bk(l,i)满足高斯分布,目标动态模型如式(1)与式(2)所示,则协作噪声满足:

(8)

(9)

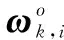
2 图理论

2.1 邻接矩阵

图G由顶点集合V和边集合E组成,假设k时刻的Gk=(Vk,Ek),其中Ek=Vk·Vk,Vk={vk,1,vk,2,…,vk,N},Vk和Ek均为非空集合。图分为无向图和有向图,区分依据是图的边是否有指定方向,有向图中的边由父节点指向子节点。

邻接矩阵用来描述顶点之间的关系,该矩阵不仅包含了图的连接关系,而且给出了图的连接方向。由于群结构与图结构的相似性,可以通过邻接矩阵来描述群的结构信息,采用非对称有向邻接矩阵描述群内相互联系的目标之间的关系如下:

(10)

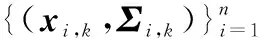
(11)

(12)

由式(12)可以看出,邻接矩阵基于两个目标之间的马氏距离进行计算,因此ak(i,j)=ak(j,i)。由于对称邻接矩阵只能获得节点之间是否有连接而不能获得节点之间的父子关系,为了判断相互连接的节点是否为父节点,可以假设在两个相互协作运动的目标中,位置靠前的节点为父节点。

2.2 HGM方法

超图是图的一种推广,与传统图一条边只能连接两个顶点不同,超图的边可以连接任意数量的顶点。超图G可以表示为G=(V,E),其中V={v1,v2,…,vp}是顶点元素的集合,E是连接一定数量顶点的超边集。一个d元组超图是所有超边连接d个顶点的超图。因此,1元组超图是顶点的集合,2元组超图是图,3元组超图是三元组的集合。图1展示了在多目标跟踪中由量测和预测点迹生成的两个超图。

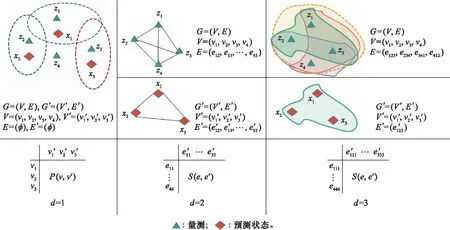
图1 量测与预测状态生成超图Fig.1 Supergraph of measurement and prediction state generation

两个超图G和G′之间的匹配是指一个顶点到另一个顶点之间的映射:V→V′,顶点匹配引入边匹配:E→E′。基于上述理论,采用HGM优化数据关联算法[20]将量测与预测状态表示为超图形式,进而通过计算顶点-顶点或超边-超边的匹配概率解决数据关联问题,具体定义如下。

(1) 顶点-顶点:当元组数d=1时,顶点之间的匹配概率根据两个顶点之间的距离来确定:

(13)

式中:v=(zk,j-h(xk∣k-1,i));Σ是v的协方差矩阵;nz是量测值数目,匹配概率表示了zk,j与xk∣k-1,i之间的相似性。

(2) 超边-超边:超边可以由相邻时刻运动矢量信息来表示,例如在二维平面跟踪问题中,2个顶点之间的欧式距离、3个顶点表示的三角形区域和4个顶点形成的2个三角形面积比分别对应d为2、3、4的超边。

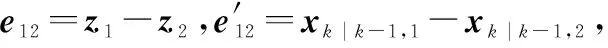
(14)

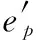
2.3 群目标估计

群的数目估计等价于子群个数的划分。文献[12]采用连通图的概念来估计子群数目,定义一个拉普拉斯矩阵:

Lk=Dk-Ak

(15)

式中:Dk表示维度的对角矩阵;dk,nk表示顶点连接的边数;Ak为邻接矩阵。拉普拉斯矩阵具有以下性质:矩阵特征值中0出现的次数就是图连通区域的个数。

在基于RFS的多目标跟踪中,滤波器的输出目标状态是随机无序的集合,而最优子模式分配(optimal subpattern assignment, OSPA)距离[24-25]可以用来表征两个集合之间的差异程度,是目前最常用的性能评价标准,并且本文采用OSPA势估计分量评估子群数目估计。

3 标签RFS与联合GLMB

标签RFS[26-29]在RFS的基础上为集合中的每个元素x∈X都分配了相应的标签l∈L,即每个目标状态用(x,l)表示,其中l=(k,i),索引i可以区分同一时刻的不同目标。则标签RFS的随机变量空间可以表示为X×L,X表示状态空间,L表示标签空间。

对所有点(x,l)∈X×L,假设其标签映射L:X×L→L为投影L(x,l)=l,有限子集X仅在X与其标签L(X)={L(x)∶x∈X}有相同基数时具有不同的标签,标签指示函数Δ(X)可表示为

(16)

3.1 联合GLMB滤波器

标准δ-GLMB[14]多目标密度先验分布具有如下形式:

(17)

式中:Ξ为给定的离散集,F(L)为标签空间子集构成的集合;I为目标轨迹标签的集合;ξ为Ξ的集合元素;(I,ξ)∈F(L)×Ξ表示δ-GLMB的一组假设分量;非负权重ω(I,ξ)=ω(ξ)(I)表示假设的可能性;p(ξ)是单概率密度。假设k-1时刻GLMB的密度如式(17)所示,则k时刻联合预测更新的GLMB[15]滤波密度表达式为

πZ+(X)∝Δ(X)·

(18)

式(18)可以看作是新生、消亡和存活的所有可能组合的枚举,以及新量测与假设标签的关联,式中I∈F(L),ξ∈Ξ,I+∈F(L+),θ+∈Θ+,并且:

(19)

(20)

(21)

(22)

(23)

(24)

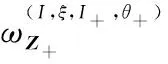
3.2 群结构的HGM应用

J-GLMB滤波算法以滤波过程中生成的假设为基础,将数据关联集成到滤波阶段,并在更新伯努利分量参数的同时基于量测位置与预测位置之间的关联概率计算假设权重,算法在具有最佳基数的假设中选取权值最高的假设提取状态。而群目标成员之间距离较近,量测和预测状态容易出现关联错误的情况,如图2(a)所示。xk∣k-1,1更接近量测zk,4,因此xk|k-1,1与zk,4的关联概率会高于其与zk,1的关联概率,出现将zk,4与xk|k-1,1错误关联的情况。

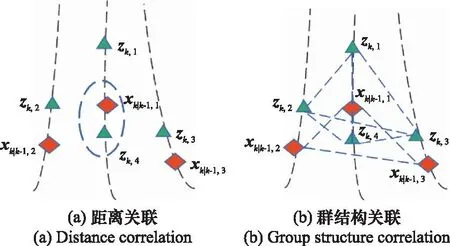
图2 距离关联与群结构关联Fig.2 Distance correlation and group structure correlation

针对上述问题,本文将HGM算法应用到J-GLMB滤波算法中,提出一种基于HGM的J-GLMB可分辨群目标跟踪算法,通过HGM、使用结构信息提升滤波阶段的隐式数据关联性能。如在图2(b)中,将量测与预测状态看作具有固定结构的群体,可以更准确地实现关联。算法将量测与预测状态以超图的形式表示,生成两个超图G=(V,E)和G′=(V′,E′),如表1所示。

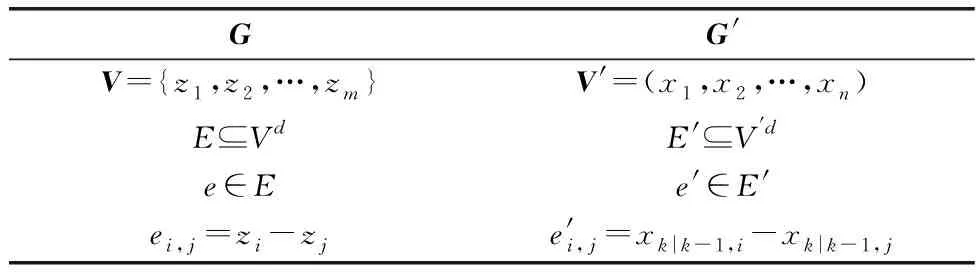
表1 超图生成Table 1 Supergraph generation

群目标跟踪中的关联问题被转化为了两个超图之间点到点的匹配问题,在J-GLMB滤波算法中,联合代价矩阵Ci,j的计算公式如下:

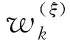
q(zj;i)=N(zj;Hmli,HPiH+R)

(26)

式中:1≤i≤I,1≤j≤J,I为k-1时刻的轨迹数,J为k-1时刻的量测数目,mli和Pi表示标签为i的目标的均值和协方差;H表示线性观测模型;R是量测噪声协方差。

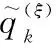
(27)

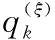
3.3 平滑算法

平滑算法利用传感器观测和滤波结果对状态向量作进一步处理,进而达到提高跟踪精度的目的。本文在需要进行状态估计的时间步,将状态提取结果传递给平滑器,即根据P1∶N对k-1时刻的状态进行平滑。同时,在前向GLMB滤波阶段之后,执行一个预平滑[30-31]阶段,设置轨迹长度阈值以消除通常由假出生引起的短期轨迹,轨迹阈值因跟踪场景而异。本文设置了线性系统场景的仿真实验,下面给出线性系统的Rauch-Tung-Striebel(RTS)平滑算法的步骤。

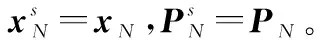
步骤 2前向滤波:计算预测值、预测协方差。

xk|k+1=Fxk

(28)

Pk|k+1=FPkFT+Q

(29)

步骤 3后向平滑:计算平滑增益、平滑状态和平滑协方差。

D=Pk+1F(Pk|k+1)-1

(30)

(31)

(32)

4 仿真实验及结果分析

仿真实验设置线性系统,通过J-GLMB、HGM-J-GLMB以及经过平滑的HGM-J-GLMB(简称为HGM-J-GLMB+平滑)3种滤波器进行实验来验证本文算法,并且对比分析OSPA距离、OSPA位置估计以及OSPA势估计。

实验在[-1 500,1 500]m×[0,3 000]m的二维区域内采用匀速(constant velocity, CV)运动模型和坐标转弯(coordinate turn, CT)运动模型对目标进行建模,杂波均匀分布在观测区域内。各个目标对应的运动状态、起始时刻和结束时刻如表2所示。

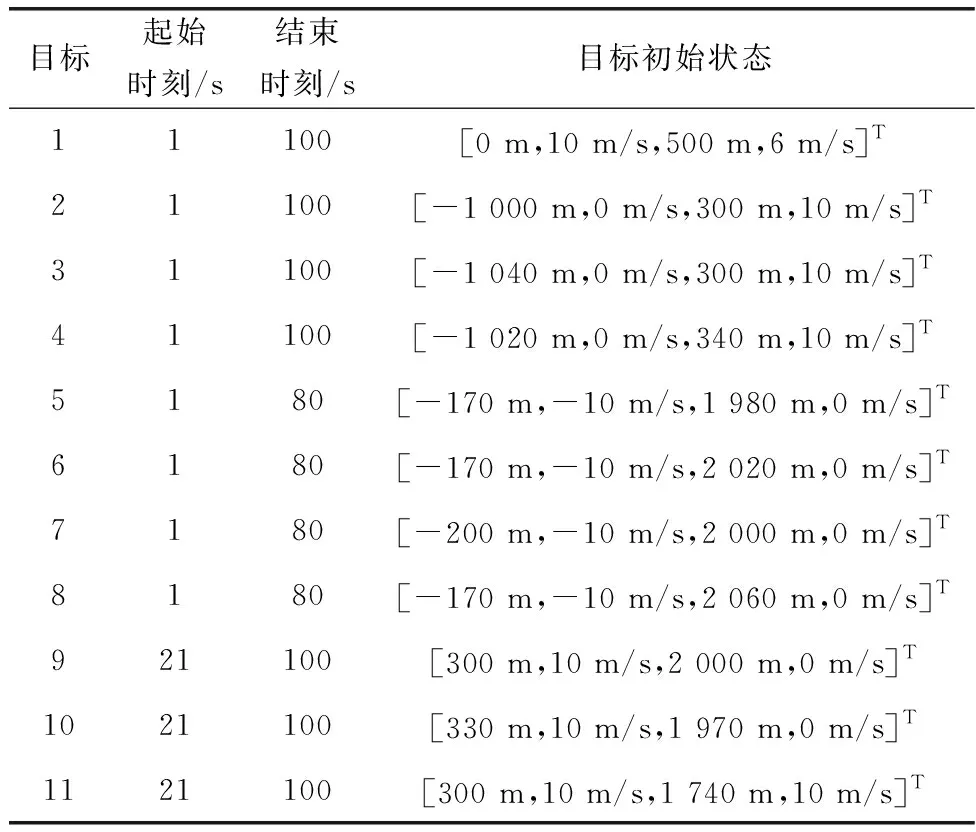
表2 各目标运动起止时刻及初始状态Table 2 Starting and ending time and initial state of each target movement

设置实验持续时间为100 s,采样周期T为1 s,根据目标的初始状态设置新生模型,假设目标的存活概率pS=0.99,检测概率pD=0.99,杂波λ=20。线性系统的状态和观测可表示为

(33)

F1和F2分别表示CV模型和CT模型的状态转移矩阵。过程噪声协方差矩阵Qk和观测噪声协方差矩阵Rk可分别表示为

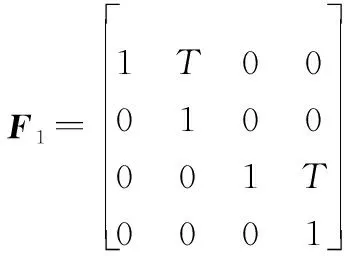
(34)

式中:σw=3 m,Mmax=1 000为仿真中伯努利分量的数量上限;Jmax=100为每个目标的高斯分量的数量上限;Tmax=10-15为剪枝阈值设置;Tlen=3为平滑阶段轨迹长度阈值。实验采用OSPA距离度量滤波性能,其参数设置为p=1、c=100。

仿真实验模拟了11个运动目标,目标运动轨迹如图3(a)所示。仿真设置目标1独立运动;目标2～目标4构成子群1;目标5～目标8构成子群2,目标5与子群2在65 s左右分离;目标9和目标10构成子群3,目标11在大约40 s时与子群3合并。图3(b)为本文滤波算法HGM-J-GLMB的估计轨迹。从轨迹可以看出,GLMB滤波算法采用标签作为目标索引区分出了目标航迹。对比图3(a)和图3(b)可以看出,估计轨迹与真实轨迹几乎重合,可知滤波器能较好地估计目标状态。

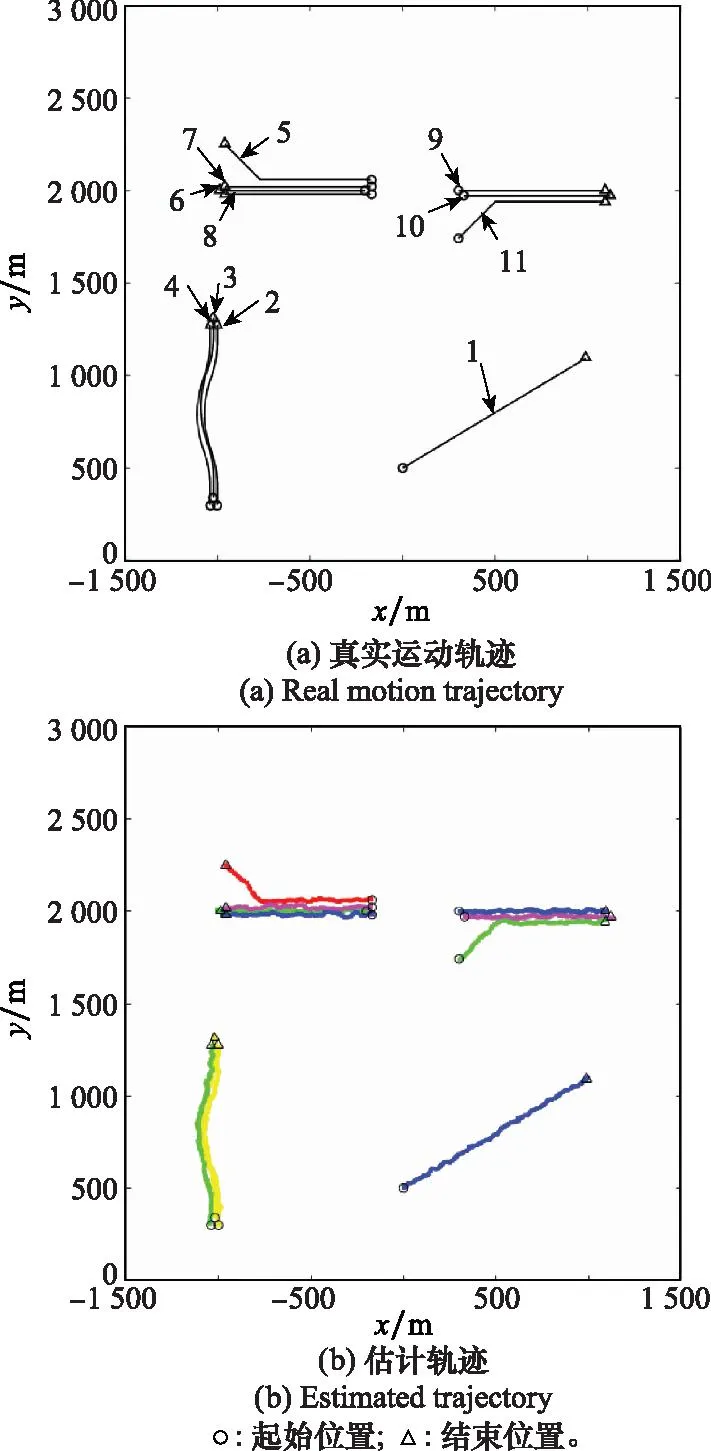
图3 真实运动轨迹与估计轨迹Fig.3 Real motion trajectory and estimated trajectory

本文结合HGM算法与J-GLMB滤波算法,将量测-预测表示为两个超图,通过HGM、使用结构信息提升滤波阶段的隐式数据关联性能。图4展示了群结构关联错误的示例。从图4可以看出,HGM-J-GLMB方法采用群结构关联,避免了关联错误的情况。相较于原有方法,HGM-J-GLMB方法对于目标估计的性能更优。

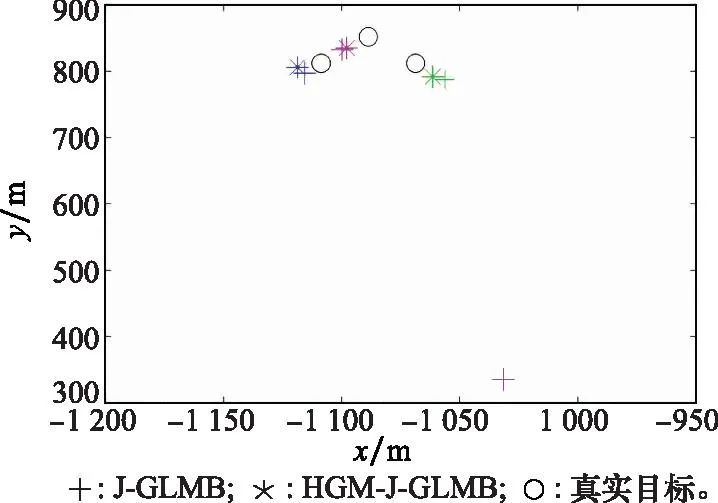
图4 群结构关联错误示例Fig.4 Example of group structure association error

本文采用OSPA距离综合评价跟踪性能,由于蒙特卡罗实验平均势估计相差太小,为便于分析,本文选取单次实验结果图分析改进的效果。单次实验的OSPA距离如图5所示,从图5的OSPA距离可以看出,在群目标跟踪场景中,HGM-GLMB滤波器的OSPA距离误差明显小于原始的J-GLMB滤波器,这意味着HGM方法可以提升目标量测与预测状态之间的关联性能,进而改善滤波效果。此外,与上述两种方法相比,经过平滑的HGM-J-GLMB滤波算法具有最优的滤波性能,并且从图5可以看出,经过平滑的滤波算法性能更加稳定,曲线更加平缓。但是,在图5中大约80 s的位置,OSPA距离出现较大的峰值,原因是滤波器对于目标死亡和目标数目下降的情况反应较慢,势估计误差增大。

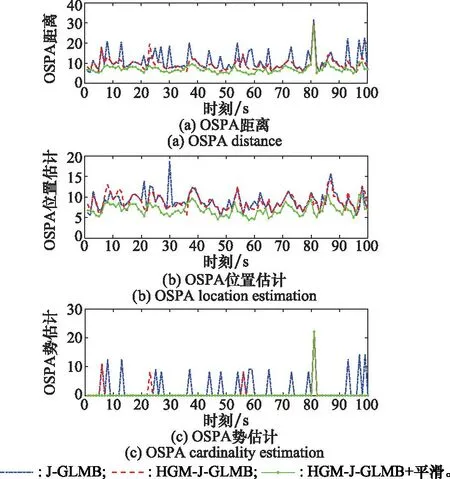
图5 OSPA距离Fig.5 OSPA distance

图5的OSPA位置估计和OSPA势估计分别显示了目标OSPA位置估计分量和OSPA势估计分量,可以看出相比于原始J-GLMB滤波器,改进的HGM-J-GLMB在OSPA位置估计出现峰值时刻曲线明显平缓,而经过平滑的HGM-J-GLMB滤波器的位置估计和势估计分量均减小,验证了本文所提算法的有效性。

图6显示了3种滤波方法的目标势估计。从图6可以看出,本文改进的滤波算法能更准确地估计出目标个数,尤其是采用平滑的HGM-J-GLMB滤波算法的势估计几乎与真实目标数重合。

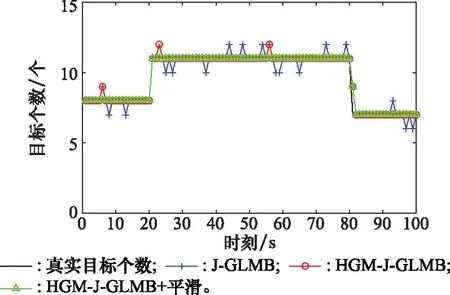
图6 势估计Fig.6 Cardinality estimation

图7为单次子群势估计。从图7可以看出3种滤波器能较为准确地估计出子群个数,但是在子群数变化的时刻,群目标势估计出现不能及时估计的情况。

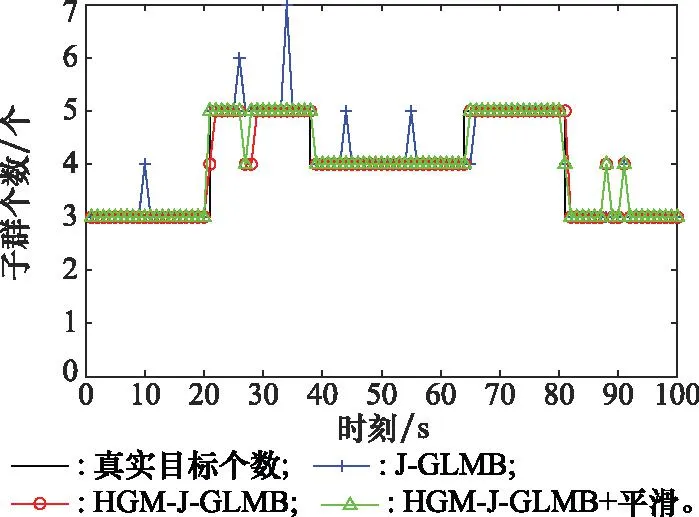
图7 子群势估计Fig.7 Subgroup cardinality estimation

本文采用OSPA势估计分量评价子群势估计,群OSPA势估计分量如图8所示。从图8可以看出,HGM-J-GLMB算法采用了HGM算法关联量测与预测状态,提升了滤波性能。而经过平滑估计的HGM-J-GLMB算法进一步提高了跟踪精度,群势估计误差明显小于另外两种滤波器。

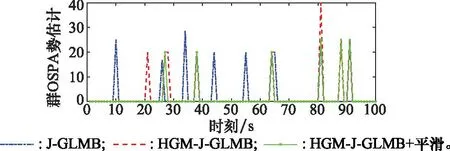
图8 群OSPA势估计Fig.8 Group OSPA cardinality estimation

表3显示了采用3种滤波器的仿真实验结果数据,包括OSPA距离、OSPA位置估计、OSPA势估计和群OSPA势估计数据。为减少数据随机性,数据为30次蒙特卡罗实验的平均结果。从表3中的数据可以看出,对比原始的J-GLMB算法,改进算法HGM-J-GLMB和经过平滑估计的HGM-J-GLMB算法在OSPA距离、OSPA势估计和群OSPA势估计上均有明显改善。其中,HGM-J-GLMB在OSPA距离上减少了6.32%,OSPA势估计减少了22.60%,群OSPA势估计减少了25.70%,验证了本文所提算法可以提升滤波性能,但是在OSPA位置估计上改进不明显。此外,与HGM-J-GLMB算法相比,进行平滑估计的HGM-J-GLMB算法在OSPA距离、OSPA位置估计、OSPA势估计和群OSPA势估计上分别进一步减少了18.35%、23.57%、1.33%以及0.14%,实验数据充分表明HGM方法和平滑估计均能提升跟踪精度。

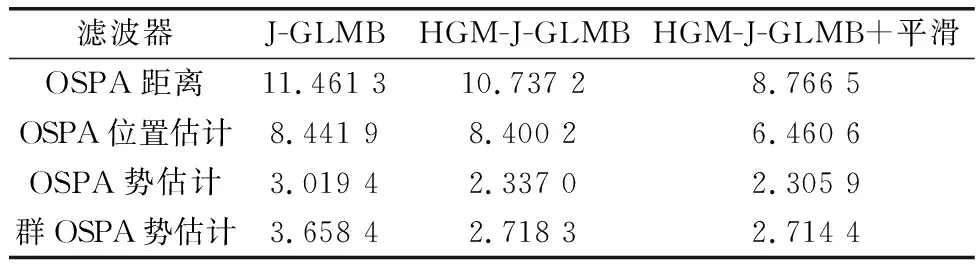
表3 线性系统平均性能Table 3 Average performance of linear system

5 结 论

本文针对距离较近的目标容易导致关联错误的可分辨群目标跟踪问题,研究了滤波算法中量测与预测状态之间的关联问题,引入HGM并提出一种HGM-J-GLMB滤波算法,提升了J-GLMB滤波中量测与预测的数据关联性能。该滤波器首先采用改进的J-GLMB滤波算法估计群内目标的状态和数目;然后,通过HGM计算邻接矩阵并估计群目标的结构和子群数目信息,基于群结构信息估计协作噪声,以校正目标状态;最后,利用RTS平滑算法提升滤波效果。在线性系统下进行的仿真实验结果表明,相比J-GLMB滤波器,本文所提算法有效提升了群目标跟踪性能,具有更稳定的目标数目估计性能。