基于注意力机制与XBOA-Bi-LSTM的离心式压缩机故障预警方法*

袁镇华,茅大钧*,李玉珍

(1.上海电力大学 自动化工程学院,上海 200090;2.上海长庚信息技术股份有限公司,上海 201209)

0 引 言

离心式压缩机是一种透平式压缩机,主要采用旋转叶片对气体进行作用,将机械能转变成静压能和动能[1]。离心压缩机在石油化工、钢铁冶炼、金属加工等工业领域发挥着至关重要的作用[2-3]。

为避免离心式压缩机突然发生意外故障和长时间停机,在故障征兆出现的早期就能做到及时发现与预警,对大型工业装备的正常运行有着重大意义[4-6]。

近年来,国内针对离心式压缩机的故障研究主要集中于离心式压缩机的故障诊断与预警方面。

HE Chang-bo等人[7]提出了一种结合多尺度噪声调谐的自适应双稳随机方法,通过双稳态随机共振对数据进行稳态分析;但该研究使用归一化尺度的方法来解决小参数限制问题,存在一定的局限性。QIU Jing-wei等人[8]研究了深度信念网络与隐马尔可夫模型,建立了基于预警系统和设备链特征分析的新型预警模型;但该研究需要完善的预警系统与具体的设备特征,因此该模型无法直接应用于工业现场进行多工况下的故障预警。陈志刚等人[9]提出了一种基于多元支持向量机的离心压缩机转子故障分类方法;但该研究并未涉及支持向量机核函数的选择与超参数的选取,其模型的准确率取决于支持向量机模型的建立情况。KARIM N等人[10]从振动分析、油液分析与运行参数三方面进行了数据融合,建立了一种基于多源信息融合与贝叶斯网络的离心式压缩机故障预警模型;但其需要统一离心式压缩机的各类故障先验概率,计算量相对较大。LI Xiao-chuan等人[11]采用典型变量计算了规范状态和残差空间的残差阈值,提出了一种基于典型变量与长短期记忆网络的动态监控方法;但在该方法的使用过程中,一方面在预测的初期受初始状态影响严重,另一方面要求训练数据量大,计算难度高。

基于以上问题,笔者首先对传统蝴蝶算法进行改建,对双向长短期神经记忆网络进行参数寻优,建立最优的神经网络预警模型;同时,采用灰色关联度结合注意力机制,构建出具有特征信息的参数序列以构建输入序列,完成离心式压缩机多种工况下的故障预警。

1 优化蝴蝶算法

1.1 蝴蝶算法原理

蝴蝶算法(BOA)是ARORA S等人[12]于2019年提出的。蝴蝶利用嗅觉、视觉、味觉、触觉和听觉寻找食物和交配对象,在这些感受器官中,最重要的就是嗅觉感受器官。嗅觉感受器官遍布蝴蝶身体的各个部位,它引导蝴蝶寻找最优的交配对象,以延续种群。

BOA算法的核心在于模仿蝴蝶的觅食和交配行为。在整个搜索空间中,每只蝴蝶都代表了一个搜索粒子。在搜索空间的不同位置,每只蝴蝶散发的香味也不尽相同,蝴蝶在接收到更高的香味浓度信号时,会自发地向香味浓度更高的蝴蝶移动。

当蝴蝶进行移动时,它的适应度函数值也会发生变化,蝴蝶散发的香味信息公式为:

f=cIa

(1)

式中:f为香味的感知强度;c为感觉通道;I为刺激强度;a为依赖于通道的幂指数,取值范围一般为[0,1]。

为了建立数学模型,笔者将蝴蝶的行为特征具体化为以下三点:

1)所有蝴蝶都会散发香味,吸引其他蝴蝶靠近;

2)每只蝴蝶都会自由移动或者朝着香味最强的蝴蝶移动,散发出更浓郁的香味;

3)蝴蝶的香味感知强度受目标函数的影响。

在BOA算法中,蝴蝶个体有两种搜索方式分别为全局搜索与局部搜索,全局搜索公式如下:

(2)

局部搜索公式如下:

(3)

1.2 算法优化

由于蝴蝶的种群初始化是随机初始化,初始解在解空间的分布随机且不均匀。基于上述问题,笔者对蝴蝶算法的初始种群进行混沌初始化,有利于蝴蝶初始种群均匀分布于解空间。常见的混沌序列为Tent映射和Logistic映射,但存在折叠次数受限和含有不动点的问题[13]。

笔者采用无限折叠迭代混沌映射(iterative chaotic map with infinite collapses,ICMIC)混沌序列对初始蝴蝶种群进行优化,ICMIC映射的数学表达式如下:

-1≤Zn≤1,Zn≠0

(4)

经过混沌初始化的种群初始位置为:

(5)

传统蝴蝶算法的全局搜索与局部搜索模式的主次由转换概率p控制,p的初始值固定为0.8,这表示传统蝴蝶算法在迭代过程中有80%的概率进行全局搜索,有20%的概率进行局部搜索。在迭代后期转换概率过高,不利于采用蝴蝶算法寻找全局最优解,无法快速收敛于某个最优解,这影响了传统蝴蝶算法的搜索效率和种群的多样性。

基于该问题,笔者提出以自适应惯性转换概率来替代传统蝴蝶算法的固定转换概率,在算法迭代的前期,较大的转换概率有利于蝴蝶个体进行全局探索,而在算法迭代的后期,将重点放在局部搜索上,这有利于蝴蝶算法进行快速收敛,同时也有利于提高蝴蝶种群的多样性。

(6)

(7)

式中:pmin,pmax为p设置的最大值与最小值;t为当前迭代次数;tmax为最大迭代次数;k(t)为种群离散度参数;aF为种群全部粒子适应度的平均值;gF为全局最优粒子的适应度;b为阻尼因子,取值范围为[0,1]。

2 注意力机制

注意力机制(AM)常被用于机器翻译的研究,其灵感来自于人类注意力机制。该机制通过扫描全局图像,获取需要重点关注的目标地区,对这一地区投入更多的注意力以获取相关细节信息,而忽视其他无关的地区。

笔者将这一思路应用于神经网络,采用AM,在众多的输入信息中聚焦于对当前任务更为影响深远的关键信息,降低对其他信息的关注度,以解决信息过载问题,同时提高任务处理的效率和准确率。

AM结构图如图1所示。

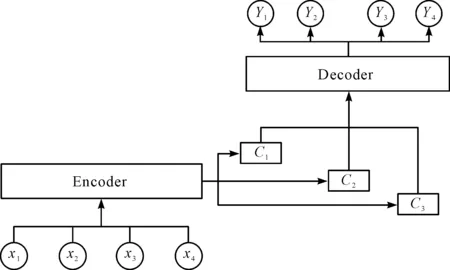
图1 AM结构图

3 双向长短期记忆神经网络

3.1 长短期记忆神经网络原理

长短期记忆神经网络(long short-term memory,LSTM)是循环神经网络(recurrent neural network,RNN)的一种类型,它解决了循环神经网络在数据训练过程中梯度消失或爆炸的问题。

LSTM在主体结构上与RNN相似,其主要的区别是在隐含层中添加了三个门控结构:遗忘门、输入门与输出门,同时也增加了一个隐藏状态[14-17]。

LSTM隐藏层结构图如图2所示。

图2 LSTM隐藏层结构图

其中,具体的计算公式如下:

f(t)=σ(Wfht-1+Ufxt+bf)

(8)

i(t)=σ(Wiht-1+Uixt+bi)

(9)

a(t)=tanh(Waht-1+Uaxt+ba)

(10)

o(t)=σ(Woht-1+Uoxt+bo)

(11)

式中:xt为t时刻的离心式压缩机状态变量;ht-1为t-1时刻的隐层状态值;Wf,Wi,Wo,Wa为遗忘门、输入门、输出门和特征提取过程中ht-1的权重系数;Uf,Ui,Uo,Ua为遗忘门、输入门、输出门和特征提取过程中xt的权重系数;bf,bi,bo,ba为遗忘门、输入门、输出门和特征提取过程中的偏置值[18];tanh为正切双曲函数;σ为激活函数Sigmoid。

经过遗忘门与输入门计算得到t时刻的细胞状态C(t)如下:

C(t)=C(t-1)⊙f(t)+i(t)⊙a(t)

(12)

式中:⊙为Hadamard积。

t时刻的隐藏层状态h(t)由输出门o(t)和当前时刻的细胞状态C(t)得出:

h(t)=o(t)⊙tanh(C(t))

(13)

3.2 双向长短期记忆神经网络原理

双向长短期神经网络(Bi-LSTM)[19]是2个独立的LSTM逆向组合而成的,将输入序列分别以正序与逆序输入至2个LSTM神经网络后进行特征提取,将2个输出向量(即提取后的特征向量)进行拼接后形成的向量作为最终特征表达。这样做不仅改善了由于LSTM前后数据信息重要程度变化而导致预测精度下降的问题,同时也使得t时刻所获得的特征数据同时拥有过去和将来的信息。

Bi-LSTM结构图如图3所示。

图3 Bi-LSTM结构图

4 数据分析与预处理

4.1 灰色关联度分析

为了充分挖掘离心式压缩机运行参数中的隐藏信息,笔者在XBOA-Bi-LSTM模型中引入注意力机制的思想,对模型中的各权重值合理分配,采用LSTM层的输入序列与输出目标之间的相关系数作为注意力系数的分配参考指标。笔者选取灰色关联度相关系数作为输入参数的各个特征,并对其分配合理的注意力系数。

灰色关联度表征数据序列间的相似度,灰色关联度与相似度成正比。假设存在离心式压缩机监控变量组成的输入序列X0={X0(1),X0(2)…X0(n)}与离心式压缩机预测变量序列Xi={Xi(1),Xi(2)…Xi(n)},则监控变量序列X0与预测变量序列Xi间的灰色关联度计算公式如下:

ξi=

(14)

式中:ρ为分辨率系数,一般取0.5。

4.2 数据归一化

由于此处采用的各运行参数间存在量纲差别,为了消除参数间的量纲影响,需要对数据进行归一化处理。

笔者采取Z-score标准化方法,其转化函数如下:

(15)

式中:μ为所有样本的均值;σ为所有样本数据的标准差。

4.3 预警阈值确定

笔者定义状态变量实际值与预测值为残差,残差的大小代表部件偏离正常工况的程度,在发生故障的前一段时刻内,残差值会表现出逐渐升高的趋势。

假设离心式压缩机某预测变量的残差序列如下:[y1,y2,y3…yN]。

在该序列的基础上,笔者选取宽度为n(n≤N)的滑动窗口,计算残差的平均值,表示如下:

(16)

笔者通过分析正常工况下的参数值分布设定预警阈值,利用滑动窗口法消除异常点对预测模型的影响,提升了故障预警模型的精度。

5 基于注意力机制与XBOA-Bi-LSTM的预警模型

基于注意力机制与XBOA-Bi-LSTM预警模型的算法流程图如图4所示。

图4 基于注意力机制与XBOA-Bi-LSTM的预警模型算法流程图

具体步骤如下:

1)从管道机组提取离心式压缩机运行参数相关数据,对数据进行预处理与归一化,将数据分为训练集、验证集、测试集与故障集(其中,归一化处理采用Z-score标准化函数);

2)根据灰色关联度分析得到的关联系数,将关联系数归一化处理后,采用注意力机制给离心式压缩机各监控参数进行赋权;

3)初始化XBOA算法,以均方根误差作为适应度函数,通过迭代获得Bi-LSTM的最优初始学习率与隐含层节点数;

4)采用最优超参数组合建立XOA-Bi-LSTM网络,将赋权后的参数序列输入到神经网络模型,使用平均绝对误差、均方根误差和线性相关系数来验证模型精度是否达到预期目标;

5)采用测试集建立XBOA-Bi-LSTM预警模型,计算并预测离心式压缩机预测变量偏离度与预警阈值;

6)引入故障集验证模型预警效果。

6 压缩机实例分析

6.1 数据分析与预处理

以某天然气长输管道机组的离心式压缩机2020年9月25日19时0分至2020年10月1日23时59分的运行数据作为实验数据。该机组压缩机是6DRSA-1型号离心式压缩机,进气压力为2.0 MPa～4.5 MPa,排气压力为4.0 MPa～6.0 MPa,额定转速为994 r/min,进口温度为10.9 ℃,排气量为151.4 Nm3/d～525.7×104Nm3/d。

离心式压缩机如图5所示。

图5 离心式压缩机

离心式压缩机进气过滤器在维持压缩机稳定运行起到了重要的作用,它一方面保证了压缩机进气的洁净质量,另一方面保障了所生产气体的洁净质量。当进气过滤器压差异常时,说明入口气体出现了严重的问题,会对离心式压缩机本体造成损伤,影响输气管道机组的经济性与安全性。

因此,笔者选择进气过滤器压差异常故障进行离心式压缩机故障预警研究,选取故障相关的测点共16个。

监控变量如表1所示。

表1 监控变量

笔者从管道压缩机组系统采集2021年9月30日01:25至2021年9月30日18:01期间共200个状态的正常历史数据,采样间隔为5 min。由于数据量纲不同,笔者采用Z-score标准化方法对数据进行归一化处理,再使用灰色关联度分析法对历史数据按关联度系数大小进行排列。

灰色关联度系数分析表如表2所示。

表2 灰色关联度系数分析表

由表2数据并结合运行工况与现场实际,笔者选取灰色关联度系数大于0.75的运行参数作为故障预警模型的输入参数,对进气过滤器压差值进行预测。

6.2 XBOA-Bi-LSTM预警模型预测结果

预测模型以进气过滤器压差1为输出结果,Bi-LSTM网络待优化超参数为初始学习率[0.001,1]与隐含层节点数[1,100]。

经过XBOA优化算法迭代可得出Bi-LSTM的最优超参数初始学习率为0.037 6,隐含层节点数为60。

XBOA-Bi-LSTM与Bi-LSTM预测模型图如图6所示。

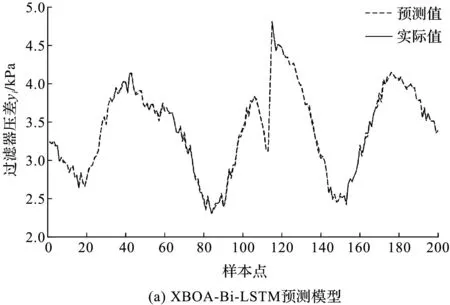
图6 预测模型对比图

预测残差对比图如图7所示。

图7 预测残差对比图

由图6、图7可以发现:XOA-Bi-LSTM预测模型相较于传统Bi-LSTM预测模型更加贴合真实值,预测残差也小于传统Bi-LSTM预测模型。

为合理评价模型预测性能,笔者采用平均绝对误差(mean square error,MAE)、均方根误差(root mean square error,RMSE)与线性相关系数(R2)作为评价标准,其数学表达式如下:

(17)

(18)

(19)

两种模型预测性能如表3所示。

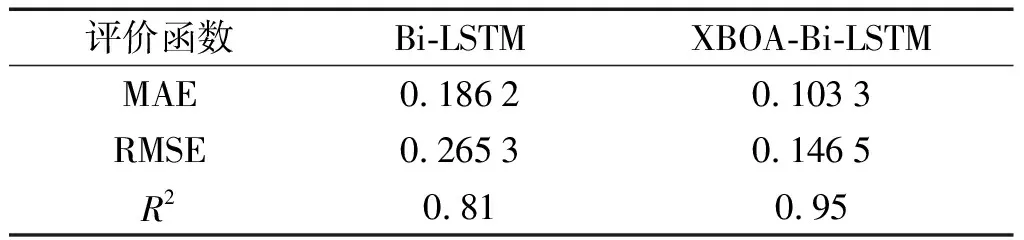
表3 模型预测性能

从表3可以看出:XBOA-Bi-LSTM预测模型性能均优于传统Bi-LSTM预测模型,证明XOBA-Bi-LSTM模型可以用于有效预测离心式压缩机运行工况。

6.3 故障预警模型验证

笔者提取离心式压缩机进气过滤器压差异常故障前后的400条数据,并将其输入到已经建立好的XOA-Bi-LSTM故障预警模型中,对进气过滤器差压2进行预测。

进气过滤器差压预测图如图8所示。

图8 进气过滤器差压预测图

由图8可以发现:通过查看进气过滤器故障记录,该压缩机进气过滤器在第329个样本点时发出压差异常报警,说明该预警模型预测误差在压差异常故障发生前就已经发生明显波动,并逐渐增大。

故障进气过滤器差压残差预测如图9所示。

图9 故障进气过滤器差压残差预测图

由图9可以发现:如果使用残差值设定固定阈值直接进行预警,在运行过程中有多个异常点,预警模型会产生较高的虚警率,导致预警结果不准确。

基于此问题,笔者采用滑动窗口法确定故障预警阈值,选取滑动窗口M=20,设置窗口滑动步长为0.5,残差阈值为0.8。每当残差平均值超过[-0.8,0.8]时,则模型发出预警,可以有效避免异常点对模型预警准确度的影响。

基于滑动窗口法的故障进气过滤器滑动窗口内差压残差平均值如图10所示。

图10 故障进气过滤器滑动窗口内差压残差平均值

由图10可以发现:滑动窗口内的残差平均值在第286个点的时候超过了预警阈值且残差发生明显跳变,说明此时进气过滤器出现故障征兆,离心式压缩机运行工况出现异常,系统发出预警,比实际报警点提前3.5 h。

事后经检查,检修人员发现进气过滤器滤芯表面和过滤网表面附着大量黑色粉尘,替换滤芯后消除了本次故障,系统恢复正常运行。

为了验证该预警模型的泛化能力,笔者选取了离心式压缩机的支撑轴承温度异常这一故障,并对其进行故障预警。笔者使用上述天然气长输管道机组的离心式压缩机2020年10月13日12时00分至2020年10月14日04时40分的运行数据作为实验数据,采样周期为5 min,共200组数据,选取故障相关的测点共12个。

监控测点如表4所示。

表4 监控测点

对数据进行归一化处理后,笔者采用灰色关联度分析法对历史数据进行处理,选取灰色关联度大于0.75的测点建立灰色关联度系数表。

灰色关联度系数表如表5所示。

表5 灰色关联度系数表

笔者以表5中3个运行参数建立XOA-Bi-LSTM故障预警模型,提取离心式压缩机径向轴承温度异常故障前后200条数据,并将其输入到XOA-Bi-LSTM故障预警模型中。

支撑轴承温度预测图如图11所示。

图11 支撑轴承温度预测图

支撑轴承温度预测残差平均值图如图12所示。

图12 支撑轴承温度预测残差平均值

由图11、图12可以发现:支撑轴承温度残差预测平均值在第114个点的时候超过了预警阈值且残差发生明显跳变,说明此时支撑轴承出现故障征兆,系统发出预警,比实际报警点提前了2.1 h。事后经检查,检修人员发现轴瓦表面存在裂纹,需要对巴氏合金进行重新浇筑,更换轴瓦后系统恢复正常运行。

综上可知,采用该方法可以实现对离心式压缩机故障的早期预警目的。

7 结束语

笔者采用注意力机制,并结合灰色关联度分析法和改进的蝴蝶算法,建立了Bi-LSTM神经网络故障预警模型,通过仿真实验,证明了采用该方法可对离心式压缩机的故障进行预警。

研究结果表明:

1)采用灰色关联度法对输入参数进行了分析,筛选出关联度更高的参数,并进行了建模,采用注意力机制对输入参数进行了赋权处理,有效提高了Bi-LSTM模型的预测精度;

2)针对传统蝴蝶算法种群多样化差与寻优能力弱的问题,提出了一种参考迭代次数与种群离散度的自适应惯性转换概率,从而提升了算法的寻优能力;其次,通过引入混沌序列提高了蝴蝶算法的种群多样性;

3)采用改进蝴蝶算法对Bi-LSTM网络超参数进行寻优,寻找最优的超参数组合,建立了Bi-LSTM预警模型。实验结果证明该故障预警方法可以用于有效预测离心式压缩机的运行工况,可以在发生故障前提前发出预警,具有实际应用价值。

目前,采用该方法可对离心式压缩机起到有效的故障预警作用。笔者后续会对离心式压缩机的振动信号处理进行研究,以实现对振动类故障进行故障预警的目的。