反应堆瞬时短周期与反应性引入速率约束问题研究

朱贵凤 严睿 邹杨 郁长清 赵学超 郭建

1（中国科学院上海应用物理研究所 上海 201800）

2（中国科学院大学 北京 100049）

反应堆周期反映了反应堆内核功率的变化速率和反应性状态，是反应堆物理试验和运行过程中需要监测的重要物理量。反应堆通常设有周期保护系统［1-7］，当反应堆周期小于安全限值时，系统将触发紧急落棒操作。

在反应堆中引入正的反应性时，由于瞬变项的影响，初始中子通量急剧上升，初始瞬时周期远低于渐进周期［8］，将可能触发短周期保护，导致一些非必要的停堆操作。目前一些核电厂采用滤波方法对周期计算进行处理［9-14］，尽可能过滤掉瞬时短周期效应。但同一算法很难在不同工况下具有普适性，而且滤波的本质是对不同时刻周期的平均，过滤加强会导致周期判断的延时性。

反应性引入速率对瞬时短周期具有较大影响，限制控制棒的提升速率成为抑制瞬时短周期现象的一些常规手段。然而，反应堆运行工况复杂，瞬时短周期还受当前反应性状态、缓发中子先驱核（Delayed Neutron Precursor，DNP）浓度等影响。从抑制短周期角度来讲，目前还没有一个约束反应性引入速率的一般方法。

本文基于点堆理论公式，推导反应性引入速率与瞬时短周期的关系，给出一个通用的、偏保守的反应性引入速率约束公式，为反应堆物理启动过程中的控制棒提升速率设置提供理论参考。

1 瞬时短周期现象

反应堆周期T(t)定义堆内中子密度增长e倍所需要的时间，计算公式为：

式中：n(t)为堆内中子密度，在实际工程中为核探测器的探测信号值。为了使用的便利性，通常把中子密度增长一倍所需时间定义为倍周期，或者称为倍周期，一般用Td表示：

在阶跃扰动下，点堆方程n(t)的解为7个指数函数的线性组合［8］：

式中：n0为常数；ωj为反应性方程的7个根，也称角频率；Aj为待定常数。当引入正反应性时，ωj中只有一个为正值，其余为负值，且Aj与ωj同号。因此，在阶跃正反应性引入初始时，由于有6组负的数值在迅速衰减，n(t)初始有一个瞬时增长过程。当达到一定时间后，该6组负值衰减殆尽，n(t)的增长由第一组正值贡献，仅与ω1相关。由式（1）和式（3）可知，此时T(t)与1ω1基本接近，称为反应堆渐进周期。

正反应性引入下的典型周期和中子密度变化趋势曲线如图1所示。本例反应性从-1×10-3阶跃引入到1×10-3，反应堆周期首先陡降，达到最低值后，又迅速增长，逐渐稳定在渐进周期。显然，初始的瞬时周期要小于渐进周期，是任何正反应性引入下的正常现象。瞬时短周期持续时间较短，对中子密度的增长推动有限，但因为其数值较小，有可能触发周期保护，而造成非必要的停堆操作。

图1 反应性从-1×10-3阶跃引入到1×10-3下的中子密度和反应堆周期变化曲线Fig.1 Neutron density and reactor period curves during the step insertion of reactivity from -1×10-3 to 1×10-3

在相同反应性引入量下，引入速率对瞬时短周期有较显著的影响。如图2所示，同样引入1×10-3反应性，引入速率越大，初始瞬时周期越小。并且在相同引入速率下，不同反应性状态下的瞬时周期也存在较大不同。因此，如何控制不同工况下的反应性引入速率，确保瞬时短周期大于保护周期限值是反应堆运行过程中一项重要的工作。

图2 不同引入速率下反应性从-5×10-4引入到5×10-4，5×10-4引入到1×10-3的反应堆周期变化曲线（彩图见网络版）Fig.2 Variation curves of reactor period under different insertion rates of reactivity from -5×10-4 to 5×10-4 and from 5×10-4 to 1×10-3 (color online)

2 反应性引入速率与瞬时周期关系推导

本节将从点堆模型推导出反应堆瞬时周期与反应性引入速率的相关性。点堆公式如下：

式中：n为中子密度；ρ为反应性；Λ为中子平均代时间；βeff为总的缓发中子有效份额，βi为第i组缓发中子有效份额；Ci为第i组先驱核浓度；λi为第i组衰变常数；Q为反应堆外源中子源强。

对式（4）两端除以n得到：

式（1）代入式（6）中有：

为了获得反应性变化率，对式（7）两边进行时间求导，得到：

继续对式（8）右边第二项做适当简化，消除Q。注意，同时根据式（7），得到，代入式（8），有：

式（9）初步建立了反应性变化率与反应堆周期的关系，但其中周期的变化率和先驱核的变化率难以观测，受不同瞬时工况影响。本节将开展一些保守假设分析，对式（9）进行简化处理。

首先将每一组先驱核浓度变化转化成指数函数形式，根据式（5）有：

其中：ωc，i为假设的Ci含时角频率，与该组缓发中子先驱核周期对应，则根据式（10）可得到：

将式（11）代入式（9）中，得到：

并简化为：

在正反应性引入过程中，由于瞬变项的影响，通常中子密度的周期要小于先驱核浓度的周期，如图3所示的周期下降段。因此，应大于任何一组ωc，i=1/Tc，i，进一步得到：

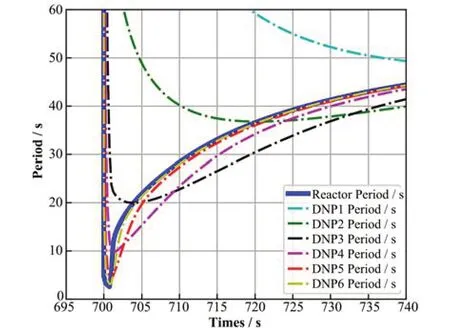
图3 反应性从-1×10-3阶跃引入到1×10-3下的反应堆周期和不同组先驱核浓度增长周期变化曲线（彩图见网络版）Fig.3 Variation curves of reactor period and rising periods of delayed neutron precursors during the step insertion of reactivity from -1×10-3 to 1×10-3 (color online)

将不等式（14）代入式（13）得到：

式（15）中最后两项合并，得到：

根据式（2）可将式（17）中的周期换算成倍周期。中子代时间和缓发中子有效份额均为常数，通过式（17）可以得到目标反应性和目标最短倍周期下的反应性引入速率约束限值。在确定需要控制的最短目标周期情况下，可以根据式（17）获得达到目标反应性需要约束的反应性引入速率。如假设最小倍周期分别为20 s、30 s、40 s、100 s，不同反应性状态下的反应性引入速率约束曲线分别如图4所示。

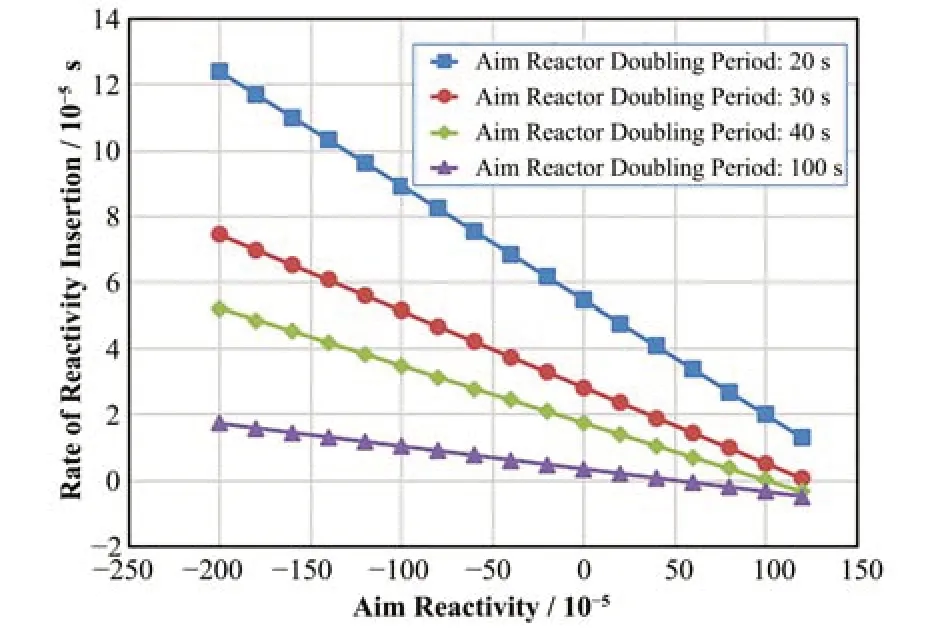
图4 不同目标最短倍周期下的反应性状态与反应性引入速率约束曲线Fig.4 Reactivity state and limit of reactivity insertion rate curve under different aims of shortest reactor double periods

在相同最短周期要求下，反应性引入速率约束值基本与目标反应性状态呈负线性关系。通过观察式（17）可以发现，该线性斜率为，截距为其中，T为目标最短周期。

当反应性引入速率为负值时，与式（14）和式（17）的近似假设不成立，因此无意义，即目标最短周期不能大于目标反应性对应的渐进周期。

当反应性为负值时，只要点堆方程中的外源价值Q、平均中子代时间和缓发中子有效份额不随反应性状态发生变化，上述推导公式依然成立。这表明，在次临界下，允许更大的反应性引入速率，而不突破相同的最短目标周期值。

3 反应性引入速率与短周期关系验证

为了验证反应性约束公式（17）的合理性，本文选取几个典型工况案例进行验证说明。首先模拟假设目标最短倍周期为20 s，反应性从-9×10-3变化到1×10-3，分10次引入，每次增加1×10-3。其中每次引入反应性速率根据式（17）计算得到，依次为33.0×10-5s-1、29.5×10-5s-1、26.1×10-5s-1、22.6×10-5s-1、19.1×10-5s-1、15.7×10-5s-1、12.2×10-5s-1、8.7×10-5s-1、5.3×10-5s-1和1.8×10-5s-1。为了比较先驱核是否平衡对倍周期曲线的影响，在每次完成反应性引入之后，设置等待时间间隔分别为10 s和100 s。据此获得两条反应性含时曲线，将其代入点堆模型中获得中子密度曲线及周期曲线。点堆模型采用python语言中的常微分方程组求解函数odeint进行计算［15-16］，动态参数采用教材［8］中的数据。计算得到的倍周期曲线如图5所示。结果表明：每次反应性引入之后，最短倍周期基本接近，约25 s，大于目标倍周期，说明采用式（17）推算出的反应性引入速率偏保守。此外，图5结果表明，不同反应性、不同等待时间下的最短倍周期变化较小，在临界后最短周期略有变化，说明缓发中子先驱核浓度在次临界下平衡时间很短，对最短倍周期影响不大。

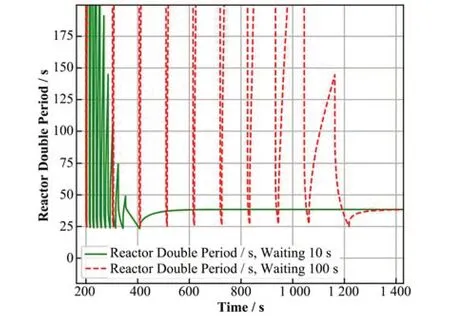
图5 反应性从-9×10-3到1×10-3下反应堆倍周期曲线（分10次引入，每次引入1×10-3，引入速率依次为33.0×10-5 s-1、29.5×10-5 s-1、26.1×10-5 s-1、22.6×10-5 s-1、19.1×10-5 s-1、15.7×10-5 s-1、12.2×10-5 s-1、8.7×10-5 s-1、5.3×10-5 s-1和1.8 ×10-5 s-1，每次间隔时间为10 s和100 s）Fig.5 Reactor double period curves during reactivity change from -9×10-3 to 1×10-3 (each 1×10-3 insertion with speed of 33.0×10-5 s-1, 29.5×10-5 s-1, 26.1×10-5 s-1, 22.6×10-5 s-1, 19.1×10-5 s-1, 15.7×10-5 s-1, 12.2×10-5 s-1, 8.7×10-5 s-1, 5.3×10-5 s-1,and 1.8×10-5 s-1, and interval time of 10 s and 100 s)

图6进一步给出了不同目标最短周期下的反应堆周期曲线，同样是反应性从-9×10-3开始，每1×10-3一个台阶引入。其中目标短倍周期40 s对应的反应性引入速率分别为15.5×10-5s-1、13.8×10-5s-1、12.1×10-5s-1、10.3×10-5s-1、8.6×10-5s-1、6.9×10-5s-1、5.1×10-5s-1、3.4×10-5s-1、1.7×10-5s-1，实际得到的最短倍周期在47～53 s范围；目标短倍周期60 s对应的反应性引入速率分别为10.1×10-5s-1、8.9×10-5s-1、7.8×10-5s-1、6.6×10-5s-1、5.5×10-5s-1、4.3×10-5s-1、3.1×10-5s-1、2.0×10-5s-1、0.84×10-5s-1，实际得到的最短倍周期在70～75 s范围。任何工况下实际最短倍周期均大于目标最短周期。

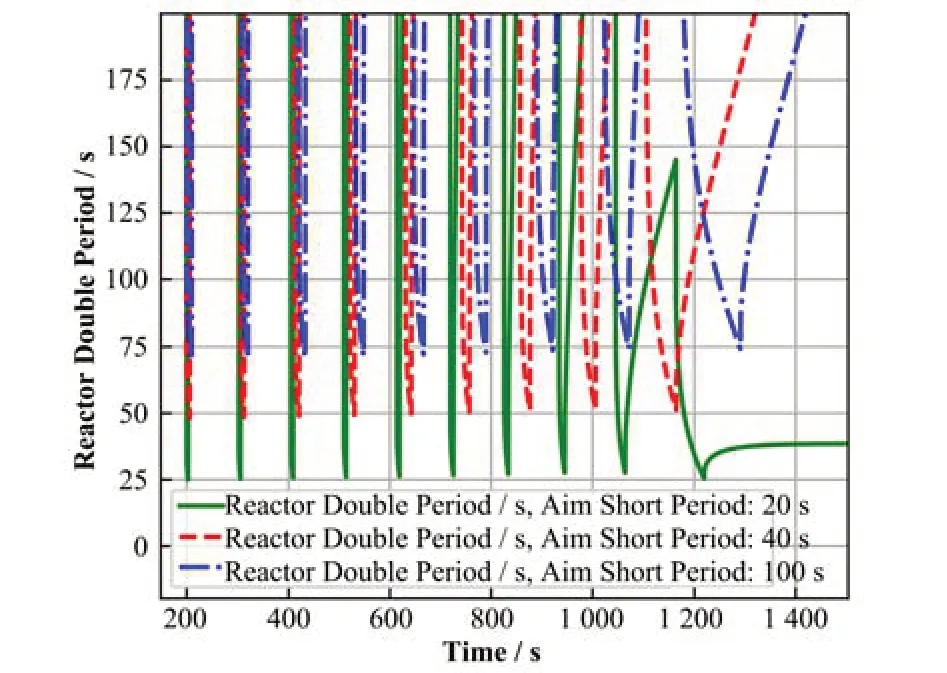
图6 反应性从-9×10-3到1×10-3下反应堆倍周期曲线（分10次引入，每次引入1×10-3，每次间隔时间为100 s，目标倍周期分别为20 s、40 s、60 s）Fig.6 Reactor double period curves during reactivity change from -9×10-3 to 1×10-3 (each 1×10-3 insertion with interval time of 100 s and aim reactor double period of 20 s, 40 s, and 60 s)

为了探明目标倍周期与实际最短周期的差异，进一步分析式（17）推导中近似处理带来的影响。以目标倍周期20 s为例，式（17）右边对反应性速率的贡献仅为0.054×10-5s-1，即使考虑为10，的贡献也仅为0.5×10-5s-1，说明对该项的去除影响可忽略；而对反应性速率的贡献达到了5.2×10-5s-1，并且随着反应性的增大而逐渐占据主导地位，说明项中采用反应堆周期代替先驱核周期的近似处理是造成目标倍周期与实际最短周期差异的主要来源。

图7展示了在缓发超临界阶段引入反应性速率与反应堆/先驱核倍周期的关系曲线，表1给出了不同目标反应性对应的最短周期时刻各先驱核倍周期以及式（14）的近似误差。结果表明，由于在缓发超临界时，先驱核没有稳定值，本身具有一定正增长周期，因此当反应性引入时，其与最短周期之间的差距并不显著，因而采用式（14）的近似处理误差要比在次临界时的小。当然，先驱核增长周期受不同瞬态工况影响，造成的近似误差都将不一样。但无论如何，式（17）保证了计算结果的保守性。

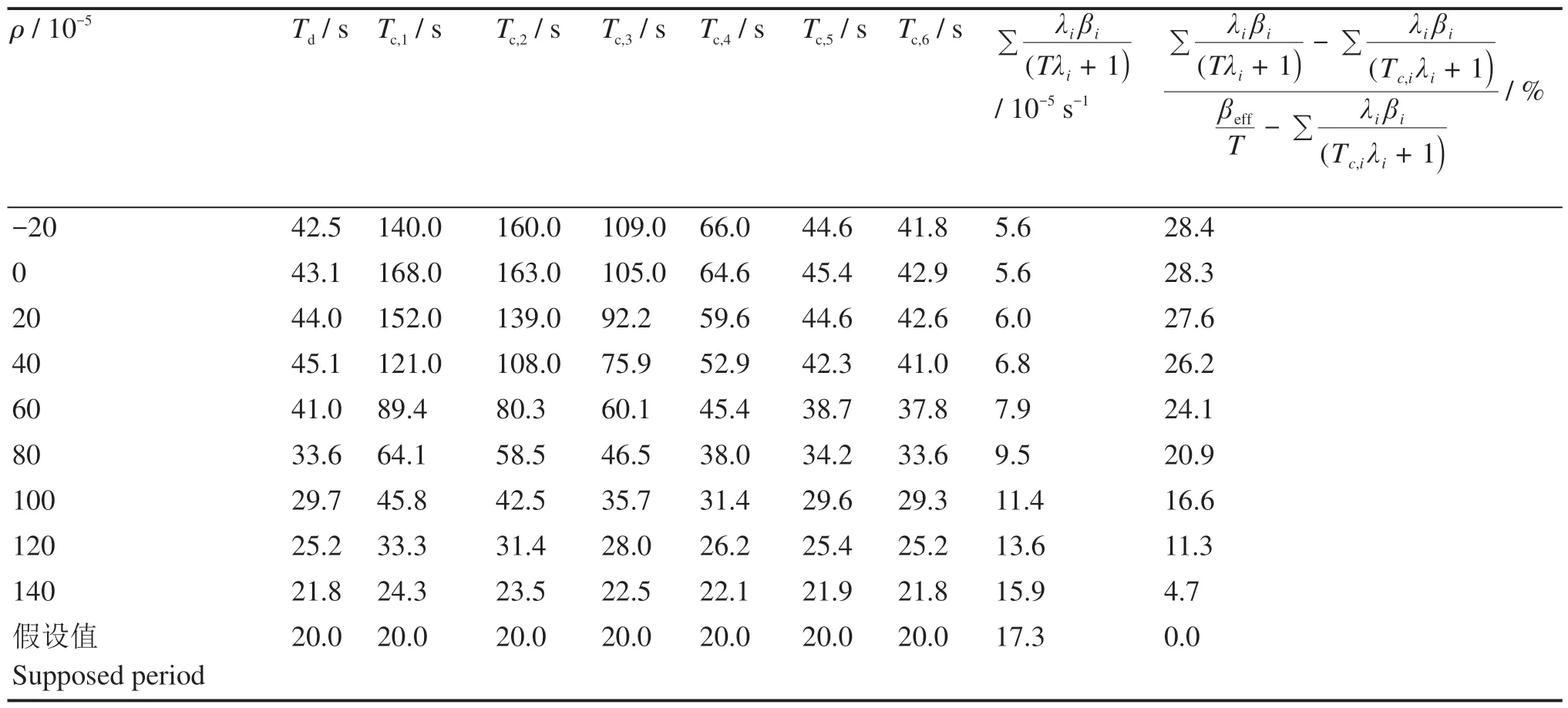
表1 不同目标反应性下最短倍周期时刻的先驱核倍周期和近似处理误差Table 1 DNP double period and processing error for different aimed reactivity cases

图7 反应性从-4×10-4到1.40×10-3下反应堆倍周期和先驱核倍周期曲线（分9次引入，每次引入2.0×10-4，每次间隔时间为100 s，目标倍周期为20 s）Fig.7 Reactor and double period curves of DNPs duringreactivity change from -4.0×10-4 to 1.40×10-3 (each 2.0×10-4 insertion with interval time of 100 s and aim reactor double period of 20 s)

4 结语

本文针对反应堆反应性引入时瞬时短周期过小而可能触发非必要的停堆问题，从点堆模型出发推导出了具有普适性和偏保守的反应性引入速率约束公式，去除了先驱核浓度变化和周期变化等实际难以测量的物理量，使得其在工程应用中具有可实施性。本文采用该公式约束下的反应性引入速率进行点堆模型验证分析，计算得到的任意周期均不会小于目标周期，且适用于次临界和缓发临界等不同工况，检验了公式的可靠性。根据该公式结合控制棒微分价值，在设定的目标周期下可以给出各种反应性工况下的控制棒提升速率约束，为反应堆物理启动中的控制棒速率约束提供了理论指导，同时也可为其他因素导致的瞬时短周期现象提供评估依据。本文对先驱核周期的处理偏保守，使得实际最短周期与目标倍周期存在一定差异，下一步工作将对此进行深入研究。

作者贡献声明朱贵凤负责研究思路、理论推导、分析数据及文章撰写；严睿对文章进行审阅及指导；邹杨提出研究课题并对文章进行指导；郁长清、赵学超、郭建等负责对公式推导复核、文字修改。