用超声衰减谱测量层状双金属氢氧化物粒度分布的方法

张明峰，吴 博，侯光昊，周 蕾，王学重

（北京石油化工学院新材料与化工学院, 恩泽生物质精细化工北京市重点实验室, 北京 102617）

随着对能源需求的提升与环保意识的增强，以氢能为代表的新能源正逐渐引起广泛关注. 利用清洁的绿电实现电化学分解水制氢一直是研究的热点，但析氧反应（OER）的缓慢速率严重制约了氢的产生与技术发展. 层状双金属氢氧化物（LDHs）作为一种非贵金属催化剂，不仅价格低廉、 来源广泛，而且对OER有良好的催化效果［1，2］. 研究发现，粒径大小对LDHs的催化效果有重要影响. 粒度过大使颗粒比表面积较小，颗粒表面活性组分减少，催化效率降低； 粒度过小则易使LDHs颗粒在催化反应过程中发生团聚而失去活性，同样对催化效果产生负面影响［3，4］. 如何快速有效地在线检测其粒度分布对于控制合成精确粒度的LDHs以及分析其电催化反应的构效关系具有重要意义. 目前，对悬浮体系中固体颗粒粒度分布的测量方法主要有以激光衍射法（LD）为代表的离线测量方法和以聚焦光束反射测量法（FBRM）为代表的在线测量方式，但上述方法在测量颗粒粒度分布时均有一定的局限性［5～10］. 离线测量法不能实时反馈颗粒在特定场景或某一时刻下的粒度分布，测量结果受分布模型影响大，且仪器造价高，分辨率低； FBRM主要测量颗粒的弦长分布（CLD），使用时需采取特定方法将CLD转换为粒度分布（PSD），且CLD受固体颗粒形状、 排列方向影响较大，会导致测量结果存在一定误差； 同时FBRM对高浓度样品颗粒的测量效果较好，而LDHs悬浮体系通常浓度较低，也会导致测量结果不准确.

超声波具备介质穿透力强、 频带范围宽、 非浸入式及简单易用等特点，在测量过程中不影响LDHs的颗粒结构和悬浮液固含量等参数特性，是一种理想的粒度测量工具［11，12］. 传统超声衰减谱法（UAS）测量悬浮体系粒度分布的原理与激光衍射法类似，当不同频率的超声波在遇到大小不同的颗粒时会发生不同程度的衰减，根据衰减数据通过模型进行反演推算，最终可得到颗粒的粒度分布［13～15］.Carlos 等［16］基于超声衰减谱实现了乳液的双峰液滴粒度分布测量，Malvern Instruments 公司开发出了UltraSizer MSV超声测量仪. 然而，上述方法和设备在使用时存在一定缺点和限制，首先测量方式为离线测量，无法对颗粒的粒度分布进行实时检测； 其次，传统UAS并不适用所有生产环境或过程中颗粒粒度分布的测量，如湿磨、 结晶和电池浆料生产等，这是由ECAH模型的作用原理决定的. ECAH模型在使用过程中存在如下假设： 分散相颗粒粒度单一且分散相和连续相的共14个物性参数已知［17］. 所需分散相的物性参数有热扩散系数（K-1）、 声衰减系数（Np/m）、 导热系数（W·m-1·K-1）、 压缩波速（m/s）、剪切模量（Pa）、 定压比热（J·kg-1·K-1）和密度（kg/m3）； 所需连续相的物性参数有热扩散系数（K-1）、 声衰减系数（Np/m）、 导热系数（W·m-1·K-1）、 压缩波速（m/s）、 定压比热（J·kg-1·K-1）、 密度（kg/m3）和剪切黏度（Pa·s）［18］. 由于LDHs 悬浮体系中分散相各物性参数未知且难以测量，连续相为水与分散剂的混合溶液，其各物性参数也难以界定，因此通过传统UAS结合ECAH模型来测量其在悬浮体系的粒度分布是不合适的.

在超声衰减谱在线测粒度领域，诸多学者做了大量的研究和工作. Falola［19］通过实验和模型建立了UAS测量体系，实时测量了研磨过程中氧化铝的粒度分布演变. Shulela等［20］基于UAS在线监测了对乙酰氨基酚结晶过程中的粒度分布. 王小康［21］基于在线超声技术对湿法研磨过程中铝碳酸镁的粒度分布变化进行了在线检测. Pertig 等［22］结合超声衰减和速度信息，用单频超声波测量了硫酸铵和尿素的粒径. 基于超声衰减谱的粒度分布在线预测方法，比传统测量方法速度更快，结果更精准，可有效避免测量对象物性参数未知且难以测定的问题，适用范围更广. 为实现对LDHs在悬浮体系中粒度分布的快速、 精准测量，避免ECAH 模型需要体系参数已知的问题，本文基于LDHs 悬浮体系的超声衰减谱，运用BP 神经网络结合主成分分析（PCA）方法建立预测模型，并引入遗传算法（GA）对模型的初始权值和阈值进行优化，通过正向预测得到了LDHs在悬浮体系中的粒度分布. CoFeAl-LDH作为一种性能优异、 结构稳定的廉价OER 催化剂，在电化学领域具备广阔的应用和发展前景，因此实验选择以CoFeAl-LDH 悬浮体系对该方法进行验证，证明了超声衰减在线预测法在LDHs 粒度表征领域的应用性能.

1 实验部分

1.1 试剂与仪器

Co（NO3）2·6H2O（纯度99.99%）、 Al（NO3）3·9H2O（纯度99.0%）和Na4P2O7（纯度99.0%），上海阿拉丁生化科技股份有限公司； FeSO4·7H2O（分析纯），国药集团化学试剂有限公司； 实验用水为去离子水.

用于验证超声衰减在线测量颗粒粒度分布的LDHs悬浮体系如下： 以水热法合成的CoFeAl-LDH为实验对象，以去离子水为溶剂，以焦磷酸钠（Na4P2O7，质量分数0.5%）为分散剂.

NanoSonic 型微纳米超声粒度仪，晶格码（青岛）智能科技有限公司； Mastersizer 3000 型激光粒度仪，马尔文帕纳科（中国）公司； DYNO®-MILL RL 型实验室用研磨机，华尔宝（机械）深圳有限公司；JW-2018H型医用离心机，安徽嘉文仪器装备有限公司.

1.2 实验过程

1.2.1 LDHs悬浮体系的制备 取一定量Co（NO3）2·6H2O，FeSO4·7H2O和Al（NO3）3·9H2O按照2∶1∶1的浓度比置于烧杯中，加入0.15 mol 尿素和300 mL 去离子水，搅拌至充分溶解，将上述溶液移装入反应釜中，在100 ℃下反应24 h. 待上述体系冷却到室温后，倒除上层清液，将固体沉淀离心3 min（转速为10000 r/min），用去离子水洗涤5 次，置于60 ℃环境中干燥24 h，研磨，过100 目筛，得到水热法合成的CoFeAl-LDH固体，其XRD表征结果如图1所示.

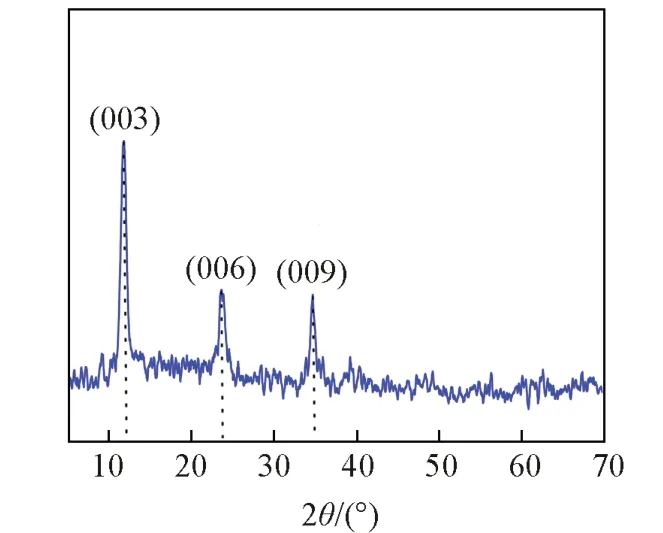
Fig.1 XRD pattern of CoFeAl-LDH

称量3.8 g LDHs固体、 1.9 g Na4P2O7和374.3 mL去离子水置于烧杯中，搅拌至溶解，制成固含量为1%的CoFeAl-LDH悬浮体系作为测量样品，备用.1.2.2 LDHs 的湿法研磨与超声衰减谱采集 湿法研磨技术作为一种自上而下的微纳米颗粒制备方法，主要通过外加应力的方式将大尺寸颗粒破碎到纳米尺寸范围，具备技术参数可控性好及所得产品粒度更小的优点［21，23，24］. 首先对制备的CoFeAl-LDH悬浮体系进行超声处理30 min，去除体系中的气泡并使LDHs颗粒分散更均匀，设置研磨机转速为3000 r/min，将悬浮液缓慢均匀倒入研磨腔，开始研磨.

研磨过程中，随着时间增加悬浮体系中LDHs 颗粒不断减小，通过高频带宽的脉冲探头进行超声波的发射和接收，利用Nanosonic 微纳米超声粒度仪对超声衰减信号进行实时采集与处理，每隔1 min进行一次超声采样，每次采样选取5～21 Hz 范围内17 个数据点进行记录，得到研磨时间分别为0，1，2，3，4，5，6，7，8，9，10 和11 min 的12 组样品的超声衰减谱图. 为减小实验误差，重复实验20 次.经Mastersizer 激光粒度仪取样检测，12组样品粒度分布范围为12～0.6 µm，此后颗粒大小基本不再随时间改变. 实验系统如图2所示.

Fig.2 Device diagram of the ultrasonic attenuation measurement system

CoFeAl-LDH颗粒活性主要由其本身性质和比表面积决定，其活性本质表现为得失电子，测量使用的超声波功率较低（10 W），且超声波的实际影响范围仅为探头间的有效长度（约43 mm），测量过程保持非浸入式，因此并不会影响LDHs颗粒的实际活性.

1.2.3 LDHs在悬浮体系中粒度分布的离线测量 通过Mastersizer 3000型激光粒度仪对每一研磨时间点CoFeAl-LDH 悬浮体系的粒度分布进行离线取样检测，所用分散剂为焦磷酸钠（Na4P2O7），每次检测前对体系进行超声处理30 min以破除颗粒团聚，根据Mie氏理论（适用于非球形颗粒），得到20次实验中不同研磨时间下LDHs悬浮体系粒度分布的离线测量结果.

为进一步确定不同研磨时间CoFeAl-LDH颗粒的粒度大小和分布，验证激光粒度仪测量结果的准确性，选择研磨时间分别为0，3，5，7，9和11 min的6组LDHs悬浮体系进行干燥和普通研磨，对研磨后的样品进行SEM测试，结果如图3所示.

Fig.3 SEM images of CoFeAl-LDH with different grinding time（A） 0 min； （B） 3 min；（C） 5 min； （D） 7 min； （E） 9 min； （F） 11 min.

根据激光粒度仪测量结果，研磨时间为0，3，5，7，9和11 min的CoFeAl-LDH的D50粒度分布结果分别为5.28，1.56，1.18，1.04，1.01和0.87 µm，D90粒度分布结果分别为11.5，3.86，2.59，2.51，2.01和1.81 µm，测量结果与SEM表征结果基本一致，说明了激光粒度仪离线测量结果的准确性，可以作为本文提出的在线测量方法的结果验证方式.

1.2.4 数据预处理 在超声衰减测量过程中，当超声频率较低或较高时均会出现数据波动情况，为取得稳定准确的数据，选择超声频率范围为5～21 MHz 下的17 个数据点构成每组LDHs 悬浮体系的超声衰减数据谱. 由Mastersizer激光粒度仪离线测得的每组LDHs悬浮体系的粒度分布谱均由100个数据点构成，若将全部数据赋值神经网络对其进行训练，会使模型需要优化的权值和阈值维度显著增加，结合数千次训练过程，整个网络将变得臃肿而复杂，造成模型预测时间成本的提升. 主成分分析作为一种高维数据处理方法，在保留数据集绝大部分特征的同时可极大降低数据维度，既简化了网络结构又可提高模型收敛性和鲁棒性，提升预测效率［25］. 因此本文尝试引入PCA 先对LDHs 粒度分布数据进行降维，将降维后的数据作为BP 网络输出对其进行训练. 实测结果表明，引入PCA 后降低了原始数据维度，使模型预测速度显著加快，而预测精度基本未受影响. 根据解释方差，选择粒度分布数据的4 个主成分（该4 个主成分可解释全部粒度分布数据99.80%的信息），作为神经网络训练集的输出值参与训练.

2 结果与讨论

2.1 超声衰减谱在线测量LDHs粒度分布

超声波作为一种经典机械波，具有波长短、 频带宽及易损耗等特点，选择超声衰减谱来测量LDHs悬浮体系中颗粒粒度分布是一种合理且精确的方法. 在实际测量中，当超声波穿过粒度大小不一的颗粒时会发生不同程度的散射和衰减. 如图5所示，超声波从I0到I的衰减程度与颗粒大小、 声波频率、探头反射距离（ΔL）以及悬浮体系的物性参数有关［26］.

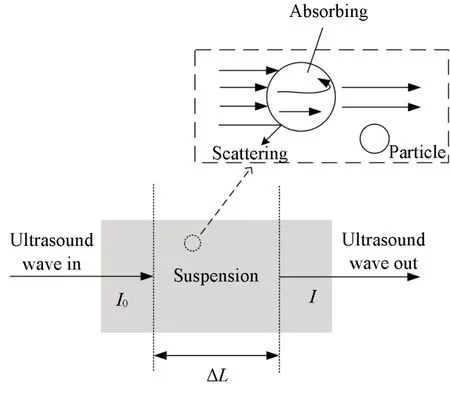
Fig.5 Schematic diagram of ultrasonic attenuation measurement

不同研磨时间下CoFeAl-LDH悬浮体系的超声衰减谱图及粒度分布离线测量结果如图6所示.

Fig.6 Ultrasonic attenuation(A) and PSD(B) of CoFeAl-LDH suspension system with different grinding time

由图6（B）可见，CoFeAl-LDHs悬浮体系的超声衰减和粒度分布随研磨时间变化均呈现一定层次差异. 随着研磨时间增加，每一悬浮体系的衰减图谱随频率变化形式整体大致相同，但不同研磨时间悬浮体系在同一超声频率下的衰减呈现下降的趋势，研磨5 min后下降趋势减缓，基本保持不变. LDHs颗粒随研磨时间增加逐渐减小，平均粒径由5.28 µm 减小到0.87 µm. 当研磨时间为0 和1 min 时，LDHs悬浮体系粒度分布谱图出现了双峰现象，这是因为初始研磨阶段悬浮体系中LDHs颗粒大小不够均匀，随着研磨时间增加，LDHs粒径大小逐渐变得均一，双峰现象消失. 对比两图发现，每一研磨时间下CoFeAl-LDHs悬浮体系的超声衰减谱均可与该体系的粒度分布谱层级对应，再次证明了通过超声衰减谱来直接测量LDHs固体颗粒在悬浮体系中粒度分布的可行性.

2.2 PCA-GA-BP神经网络模型的搭建

为克服超声衰减谱法应用的局限性，采用BP神经网络结合主成分分析的方法建立了预测模型，并引入遗传算法对模型的初始权值和阈值进行优化. BP神经网络作为一种多层前馈神经网络，具备柔性的网络结构和很强的非线性映射能力，目前无论在理论还是性能方面都发展得较为成熟，被广泛应用于分类、 回归和模式识别等工业领域［27］. 本文通过MATLAB R2022a软件实现预测模型的编程.

实验收集了研磨时间分别为0，1，2，3，4，5，6，7，8，9，10和11 min的CoFeAl-LDH 悬浮体系的超声衰减和粒度分布数据，首先利用mapminmax函数对数据进行［-1，1］范围的归一化，避免由于命令输入和权重的两极化引起数值问题，使网络快速收敛，提升预测速度［28］. 以研磨时间分别为0，2，3，5，6，8，9和11 min的8组LDHs悬浮体系超声衰减和粒度分布数据作为网络训练集，引入PCA对粒度分布数据进行降维. 通过tansig 函数构建输入层，以purelin 函数构建输出层，设置不同隐含层数进行仿真测试. 结果表明，随隐含层数增多，BP网络训练时间会极大增加，但预测精度并未出现显著提高或下降，因此最终选择设置隐含层数为1，通过newff函数创建单隐含层BP神经网络.

BP 神经网络输入层和输出层节点的数量均取决于已有的样本数据训练集，本研究中网络输入层节点数等于输入样本（超声衰减数据）所包含的参数个数为17，输出层节点数等于输出样本（粒度分布数据）PCA降维后所包含的参数个数4［29］，隐含层节点数可通过式进行确定，其中m和n分别是网络输入层与输出层节点数，a为调节常数（a∈[1，10]）［30］，设置不同隐含层节点数得到的拟合结果均方误差对比如表1所示：

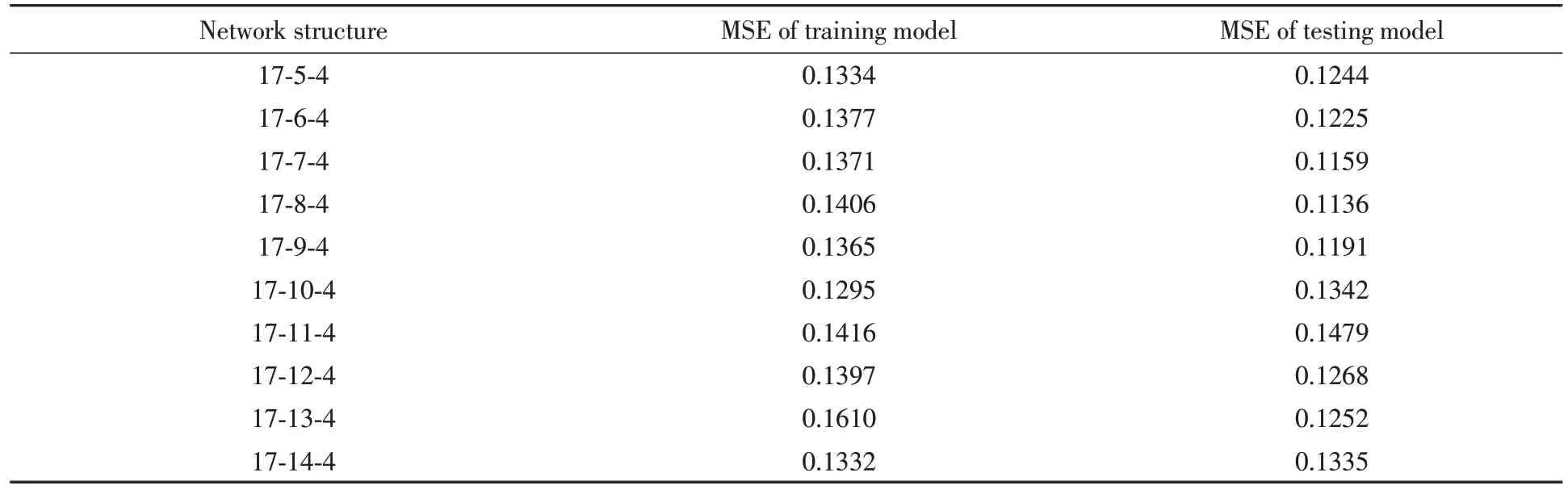
Table 1 Mean square error（MSE) of different network structure models

当隐含层神经元节点数目过少时，神经网络无法拟合复杂的映射关系，过多时又会导致过拟合，使最终预测结果出现较大偏差. 依照同等预测精度下尽可能提升预测效率的原则，通过多次训练对比决定选择“17-5-4”型网络结构搭建PCA-GA-BP 神经网络. BP 神经网络的一个缺点是易将局部最优解选作全局最优解，为解决这一问题引入遗传算法（GA）对模型进行优化. GA作为一种启发式算法，其原理为通过模拟自然进化过程来搜索全局最优解，可同时使用多点搜索信息，具有很好的全局收敛性和搜索能力，可极大增强模型鲁棒性和泛化能力［31，32］. 设置GA的最大遗传代数为250代，种群规模为50，交叉率为0.5，变异率为0.001.

图7呈现了模型的3种主要构成方法即PCA，GA与BP神经网络三者之间的组成联系和作用方式.整个模型作用原理如下： PCA 首先对LDHs 粒度分布数据进行降维，然后用BP 对网络参数（权值和阈值）进行初始化，由GA 对初始参数编码，然后利用样本数据通过轮盘赌算法对网络参数不断进行选择、 交叉和变异，直到找到满足约束条件的最佳参数并将其重新赋值给BP神经网络，BP神经网络以该参数作为最优初始参数开展正式训练，直到预测结果满足最小误差条件.

Fig.7 Structure diagram of PCA-GA-BP neural network model

2.3 PCA-GA-BP神经网络模型的训练

以研磨时间分别为0，2，3，5，6，8，9和11 min的8组LDHs悬浮体系的超声衰减和粒度分布数据作训练集. 首先利用GA对模型的初始权值和阈值进行最优寻值，如图8所示，随遗传代数增加GA不断对网络参数进行迭代与更新，网络最佳适应度Best fitness（训练误差）不断减小，直到达到最小值0.1034 不再发生改变，说明神经网络的权值和阈值已为最优，模型具备了最佳学习效果. 将此时的权值和阈值赋值给BP网络，作为训练的初始参数，设置训练次数为3000，保证训练效果的充分性. 设置学习速率为0.01，最小目标误差为0.001，应用训练集数据对模型开展充分训练. 结果发现： 训练模型拟合优度R2=0.9919，均方误差为0.1334，表明神经网络已经具备良好的学习能力.

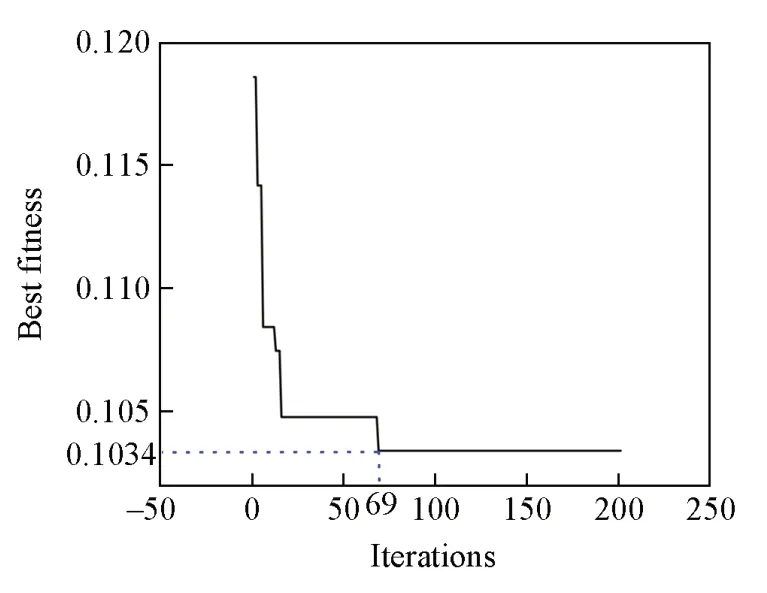
Fig.8 Best fitness varies with iterations

2.4 PCA-GA-BP神经网络模型的验证

将研磨时间分别为1，4，7和10 min的CoFeAl-LDHs悬浮体系超声衰减数据输入模型，模型自动输出4组体系中LDHs的粒度分布. 将模型预测结果与通过Mastersizer 3000型激光粒度仪离线测量的4组LDHs粒度分布结果进行对比验证，得到的相应体系粒度分布和累积粒度分布拟合结果如图9所示.

验证结果表明，对于研磨时间为1，4，7 和10 min 的4 组CoFeAl-LDH 悬浮体系，通过PCA-GA-BP神经网络模型进行预测得到的粒度分布结果与真实结果峰形相似，峰高相近. 通过体积密度累加计算得到了4组LDHs悬浮体系的累积粒度分布，如图10所示，4组验证体系累积粒度分布的体积分率绝对误差最大为0.0746，最小为-0.0218，相对误差最大为0.9640，最小为0.0042，可见绝对误差和相对误差均在可接受范围内. 实验还分别计算出4组验证体系累积体积分率达到D10，D50和D90时粒径的绝对误差与相对误差，绝对误差最大为0.1633 µm，最小为0.0012 µm，相对误差最大为0.2908，最小为0.0034. 为展示模型整体预测效果，实验最终计算出4组验证体系粒度分布的模型预测结果与实际测量结果的总均方误差MSE 为0.1497，模型拟合优度R2=0.9768，说明PCA-GA-BP 神经网络对CoFeAl-LDHs在悬浮体系中的粒度分布具备准确的测量效果.

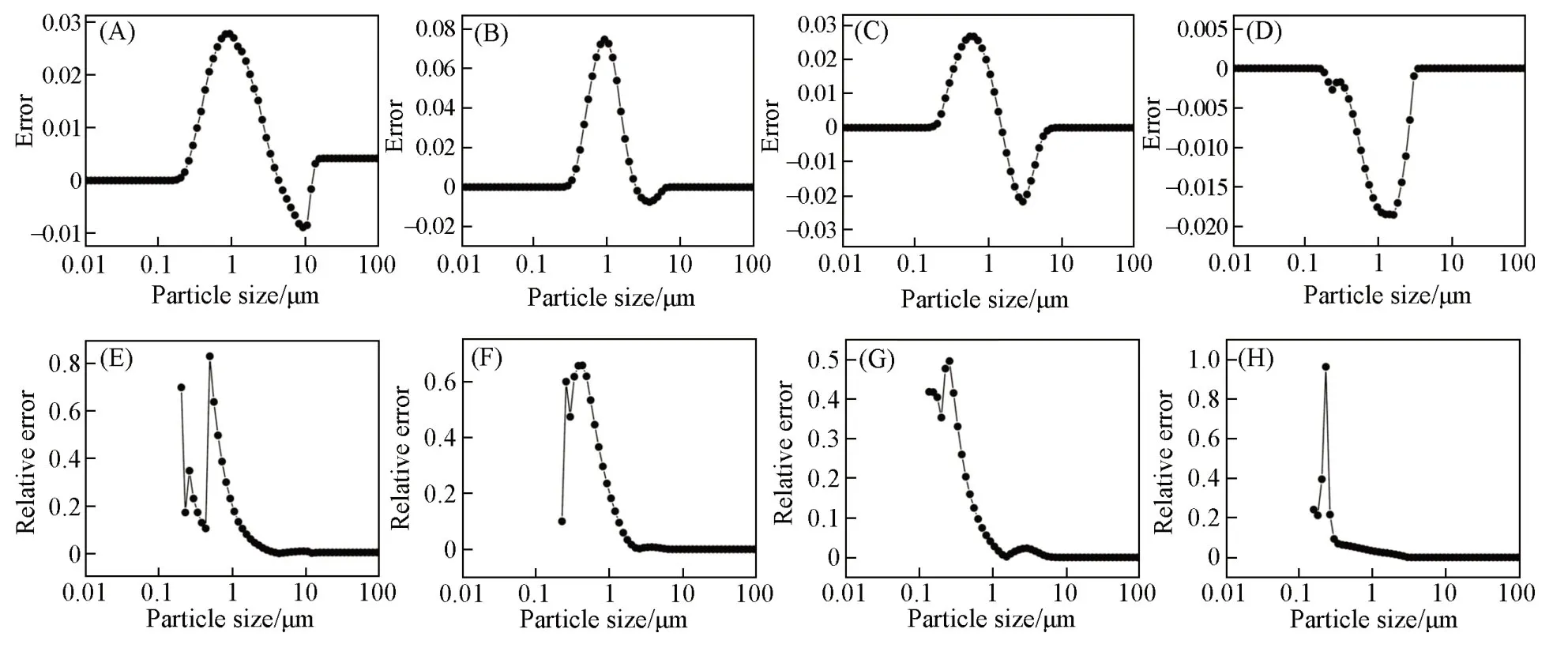
Fig.10 Error(A—D) and relative error(E—H) of the cumulative PSD of CoFeAl-LDH verification system（A，E） 1 min； （B，F） 4 min； （C，G） 7 min； （D，H） 10 min.

本研究通过水热法合成了MgAl-LDH，对其进行了XRD表征，利用湿法研磨技术制备了12组不同研磨时间下的MgAl-LDH 悬浮体系，利用本文方法实现了对不同研磨时间下MgAl-LDH 在悬浮体系中粒度分布的在线检测. 计算出4 组MgAl-LDH 验证体系累积粒度分布的体积分率绝对误差最大为0.0632，最小为-0.0473，相对误差最大为0.8362，最小为0.0050，模型预测结果与实际测量结果的总均方误差MSE 为0.1647，模型拟合优度R2=0.9479，证明该方法具备良好的普适性. 相关分析测试和对比数据结果已列于本文支持信息中.

3 结 论

以不同研磨时间下的CoFeAl-LDH在悬浮体系中的超声衰减谱为基础，结合主成分分析搭建BP神经网络，并引入遗传算法对网络参数进行优化，首次实现了对CoFeAl-LDH和MgAl-LDH在悬浮体系中粒度分布的在线测量. 将PCA-GA-BP 神经网络预测结果与通过Mastersizer 3000 型激光粒度仪离线测量的结果进行了对比分析，预测模型拟合优度R2分别达到0.9768 和0.9479，说明超声衰减谱可以对LDHs 在悬浮体系中的粒度分布实现在线精准测量，解决了传统超声衰减谱法通过ECAH 模型测量颗粒粒径首先需要被测体系物性参数已知的问题，该测量过程快速、 结果精准. 对于分散相为纳米级LDHs或其它微纳米颗粒的悬浮体系，仅需改变部分测量条件，即可用该方法进行测量，结合Boubenia等［33］的研究结果，通过对超声探头的制作材料进行改进，预期可以实现对LDHs等颗粒的合成过程实现在线精准控制. 这为精确粒度大小颗粒的合成检测与过程控制提供了新思路，有利于制氢和颗粒分析表征技术的发展，在光、 电及热催化等领域均有较好的应用前景.

支持信息见http: //www.cjcu.jlu.edu.cn/CN/10.7503/cjcu20230463.