Sliding behaviors of the trapezoidal roof rock block under a lateral dynamic disturbance
Feng Di,Wncheng Zhu,Min Ren,Shunchun Wu,Leilei Niu
a Faculty of Land Resources Engineering, Kunming University of Science and Technology, Kunming, 650093, China
b Center for Rock Instability and Seismicity Research, Department of Mining Engineering, School of Resource and Civil Engineering, Northeastern University,Shenyang,110819, China
Keywords: Lateral dynamic disturbance Trapezoidal rock block system Low-velocity and low-frequency wave Friction reduction effect Instability mode
ABSTRACT The surrounding rock of underground space is always affected by external dynamic disturbance from the side position,such as blasting vibration from a stope at the same level or seismic waves from adjacent strata.A series of laboratory tests,numerical simulations and theoretical analyses were carried out in this study to disclose the sliding mechanism of roof rock blocks under lateral disturbance.Firstly,the experiments on trapezoidal key block under various clamping loads and disturbance were conducted,followed by numerical simulations using the fast Lagrangian analysis of continua (FLAC3D).Then,based on the conventional wave propagation model and the classical shear-slip constitutive model,a theoretical model was proposed to capture the relative displacement between blocks and the sliding displacement of the key block.The results indicate that the sliding displacement of the key block increased linearly with the disturbance energy and decreased exponentially with the clamping load when the key block was disturbed to slide (without instability).Meanwhile,when the key block was disturbed to fall,two types of instability process may appear as immediate type or delayed type.In addition,the propagation of stress waves in the block system exhibited obvious low-velocity and lowfrequency characteristics,resulting in the friction reduction effect appearing at the contact interface,which is the essential reason for the sliding of rock blocks.The results can be applied to practical underground engineering and provide valuable guidance for the early detection and prevention of rockfalling disasters.
1.Introduction
Due to the increasing demand for underground space in mining,subway,tunnel,carbon dioxide storage,nuclear waste storage and other engineering,the geological disasters of underground rock mass,particularly roof rock collapse,are becoming more frequent(Esterhuizen and Streuders,1998).The rock mass is a complex natural material composed of rocks and discontinuities (Hoek and Bieniawski,1984),including flaws,joints,intercalations,material interfaces,faults,and fractures(You et al.,2022).For the intact rock,failure emerges primarily as the commencement and growth of fissures due to stress concentration (Tang,1997).However,the underground rock mass is typically segmented by several discontinuities and can even be considered as a block system composed of separate rock blocks (Goodman and Shi,1985;Shi and Goodman,1989),especially for the surrounding rock in the excavation disturbed area.Since the bearing capacity of discontinuities is much lower than that of an intact rock block,the instability of the jointed rock mass generally manifests as the sliding of rock blocks along the structural planes(Chen et al.,2019).
In underground engineering,the instability of rock block systems is mainly induced by external disturbance (Lu et al.,2013),including static disturbance(e.g.underground water,local tectonic stress,and underground space excavation) and dynamic disturbance(e.g.earthquake,blasting,and mechanical vibration).Among them,external dynamic disturbance is the most direct and dangerous factor(Ma et al.,2009;Liu et al.,2018;You et al.,2022).In addition,the direction of disturbance propagation also plays a key role in the disturbed instability of rock mass.When the spatial position of the disturbance source relative to the disturbed rock mass is different,the dynamic disturbance transmitted in various directions will result in a discernible change in the instability mechanism(Kocharyan et al.,1994).For example,when blasting is carried out in upper-level stopes,the vertically transmitted dynamic disturbance may cause the instability and collapse of jointed rock mass in the roof of the excavation space below(Yi et al.,2017).Based on the laboratory experiments and numerical simulations,Dai et al.(2021) analyzed the instability process of a rock block subjected to a vertically propagated disturbance and concluded that the primary mechanism of its instability is the sliding driving effect of the dynamic disturbance.However,in the underground mining exploitation design,it is more popular for numerous stopes operating at the same depth (Liu et al.,2019).In this case,the blasting operation in the sideway stope may impact the roof stability of the existing excavation space (Liu et al.,2021).Besides,tunnel construction frequently involves double tunnel excavation,and the dynamic disturbance caused by lateral blasting can contribute to the instability of neighboring tunnel roofs (Ye et al.,2011;Oliveira and Diederichs,2017;Wu et al.,2019).
For the lateral dynamic disturbance induced sliding and instability of rock block system,some scholars believed that it is related to the pendulum-type wave and ultra-low friction effect,which was discovered by Kulenya et al.(1996a) during the underground blasting tests.It is found that when the jointed rock mass far away from the blasting source was subjected to the blasting disturbance,the distance between rock blocks presents a positive-negativealternating periodic oscillation,which is called the “pendulumtype wave”(Kurlenya et al.,1996a,b,c).Meanwhile,the friction of the contact surface between rock blocks easily reduces or occasionally disappears,which is called the “ultra-low friction effect”(Kurlenya et al.,1996b).Since this discovery was proposed,many scholars have been researching the pendulum-type waves and the ultra-low friction effect for years.They not only proposed several theoretical models for the dynamic propagation in rock block systems (e.g.the elastic model (Kocharyan and Spivak,2001;Kocharyan et al.,2001),the elastoplastic model (Chanyshev and Efimenko,2003a,b,2004;Chanyshev et al.,2005),the viscoelastic model (Aleksandrova,2003;Aleksandrova et al.,2006,2008),the energy storage considered model(Wang et al.,2005),the second-order frequency considered model (Sher et al.,2007) and the Hertz-contact considered model (Wang et al.,2007)) but also analyzed the impact of numerous parameters on the pendulumtype wave (e.g.the factors of interface friction coefficient (Li et al.,2009),the rock block size (Pan and Wang,2012),the interface viscoelasticity (Wang and Pan,2013;Wang et al.,2013),the weak interlayer (Jiang et al.,2019a),the stress boundary (Li et al.,2014) and others),and even effectively used the pendulum-type wave theory to explain phenomena and solve problems in several domain engineering (e.g.the earthquake and underground explosion hazard assessment (Adushkin and Oparin,2012,2013,2014,2016;Oparin et al.,2018;Wang and Li,2019),the stability analysis of surrounding rock of chamber sidewall (Wu et al.,2009),the roadway support design (Pan et al.,2013;Tang et al.,2015) and other aspects).In general,the invention of pendulum-type wave theory provides a helpful theoretical foundation for understanding the mechanism of jointed roof rock mass caving.
In the conventional pendulum-type wave theory,the formation of pendulum-type waves is subjected to stringent evaluation criteria(Kurlenya et al.,1996b,c,1998;Kurlenya and Oparin,1999,2000).According to the reaction of rock mass remote from the explosion source to blasting disturbance,an energy requirement was established,and it was required that the disturbance energy for creating a pendulum-type wave should be confined to a particular range(Kurlenya et al.,1996c).Therefore,most research on the instability of rock block system under lateral dynamic disturbance was carried out under the low-energy disturbance(i.e.the magnitude of energy is mJ) (Kurlenya et al.,1996b;Deng et al.,2018;Jiang et al.,2019b;Li et al.,2020;Shi et al.,2020).However,the essence of disturbed rock block system instability is the resonant or quasi-resonant response of rock blocks (Kurlenya et al.,1998;Li et al.,2018),and the primary influencing factors should be the frequency distribution of dynamic disturbance and the natural frequency of rock block system.In the same frequency components,the disturbance with higher energy will result in a more pronounced resonance of the rock block system and induce the instability of jointed rock mass more easily.Therefore,the high-energy dynamic disturbance will also impair the stability of the jointed rock mass around the explosion site,even though the subjected stress is lower than the dynamic failure strength.In addition,the conventional research on rock block system stability under dynamic disturbance mainly focused on the rectangular block (Deng et al.,2018;Li et al.,2018,2020,2022;Jiang et al.,2019b;Shi et al.,2020),while disregarded the more prevalent trapezoidal rock block (González-palacio et al.,2005).Thus,studying the sliding mechanism of the trapezoidal rock block system under high-energy lateral dynamic disturbance is necessary.
This study uses laboratory tests,numerical simulations and theoretical analyses to investigate the sliding and instability process of the trapezoidal rock block system under high-energy lateral disturbance and low in situ stress conditions.By using the selfdeveloped dynamic disturbance test equipment,the disturbed tests of the trapezoidal rock block system are conducted under various clamping loads and different disturbance energy levels to observe the sliding process.Then,through utilizing the benefits of the numerical approach,the propagation law of the disturbance stress wave in the block system is examined to disclose the basic mechanism of block sliding and instability.Finally,the relative displacement model between blocks and the sliding displacement model of the trapezoidal key block under lateral dynamic disturbance is developed based on the classical elastic wave propagation model and the sliding friction model.Meanwhile,the reliability of the theoretical model proposed in this study is confirmed by comparing experimental and numerical results.
2.Laboratory experiment
2.1.Experimental preparation
The homogeneous natural sandstones sampled from the same region in Sichuan Province of China are selected for the experiments.The basic mechanical parameters of the sandstone are listed in Table 1,which are obtained by standard laboratory tests (i.e.uniaxial compression tests,Brazilian-splitting tests,and direct shear tests).As can be seen in Fig.1a,the surrounding rock on the left,the key block in the middle,and the surrounding rock on the right are divided using a diamond wire cutter.

Fig.1.Three-dimensional (3D) laser scanning of sandstone cutting surface: (a) Trapezoidal rock blocks and size,and (b) Scanning of cutting surface with 3D laser equipment.

Fig.2.3D scanning results of roughness of rock sample cutting surface:(a)Right surface of the left rock block,(b)Left surface of the middle key rock block,(c)Right surface of the middle key rock block,and (d) Left surface of the right rock block.

Table 1 Basic mechanical parameters of sandstone.
In order to ensure that the cutting surface roughness of each rock block is consistent,the spindle speed and propulsion speed of the wire cutting machine are set to 4 m/s and 0.1 mm/s,respectively.As can be seen in Fig.1b and 2,a 3D laser scanning devicewas used to scan and sample the rock surface to determine the cutting surface roughness.By using a joint roughness coefficient(JRC) calculation method proposed by Liu et al.(2017),the roughnesses of the left block’s right-side surface,the middle block’s biside surfaces and the right block’s left-side surface are 1.7091,1.741,1.223 and 1.3238,respectively.In addition,a series of shearslip tests was conducted on standard-sized sandstone samples,which were cut in the same way as the trapezoidal rock block,to evaluate the uniformity of the friction performance of these surfaces,as shown in Fig.3.According to Table 2,since the roughness of the standard sample is similar to that of the trapezoidal rock block,it can be assumed that the shear and slip performance of the trapezoidal rock block will be roughly identical with that of the standard sample.

Fig.3.Specimen for rock structural plane shear test: (a) Standard specimens for shear-slip test,and (b) Upper and lower surfaces of specimen S-6.
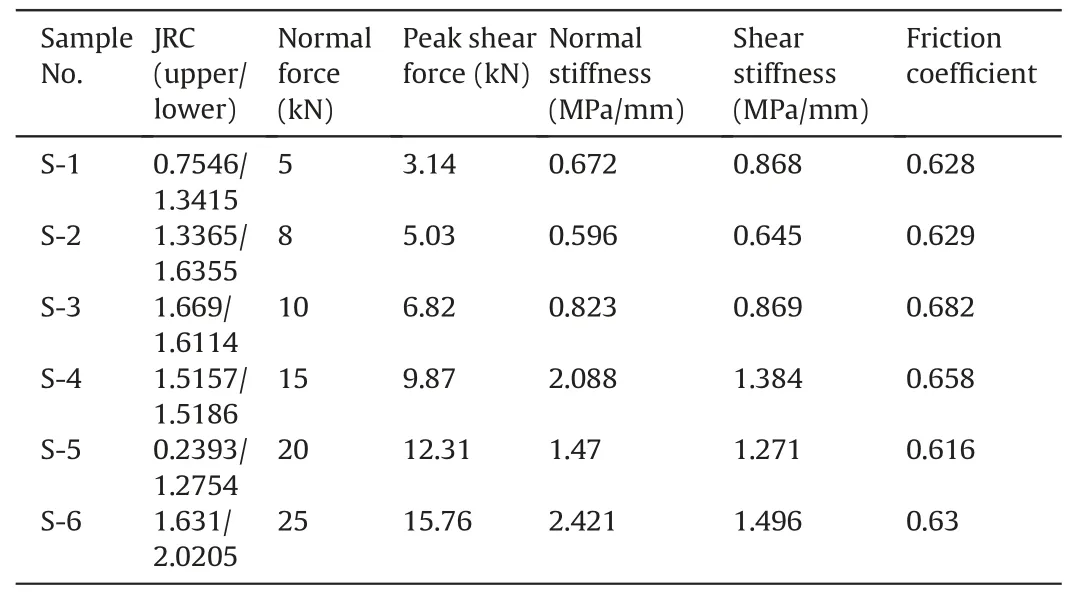
Table 2 Mechanical parameters of rock cutting surface.
2.2.Experimental schemes
The loading process can be divided into two stages.Firstly,the hydraulic cylinder is used to apply the quasi-static lateral clamping force,which is meant to mimic the in situ stress in an underground environment and maintain the initial stability of the rock block system.Next,a swing hammer is used to apply a lateral impact disturbance to the block system for simulating the effect of dynamic disturbance,for example a blasting operation from the sideway.Fig.4 depicts the sample’s boundary conditions and the testing apparatus.The specific test operation steps are as follows:
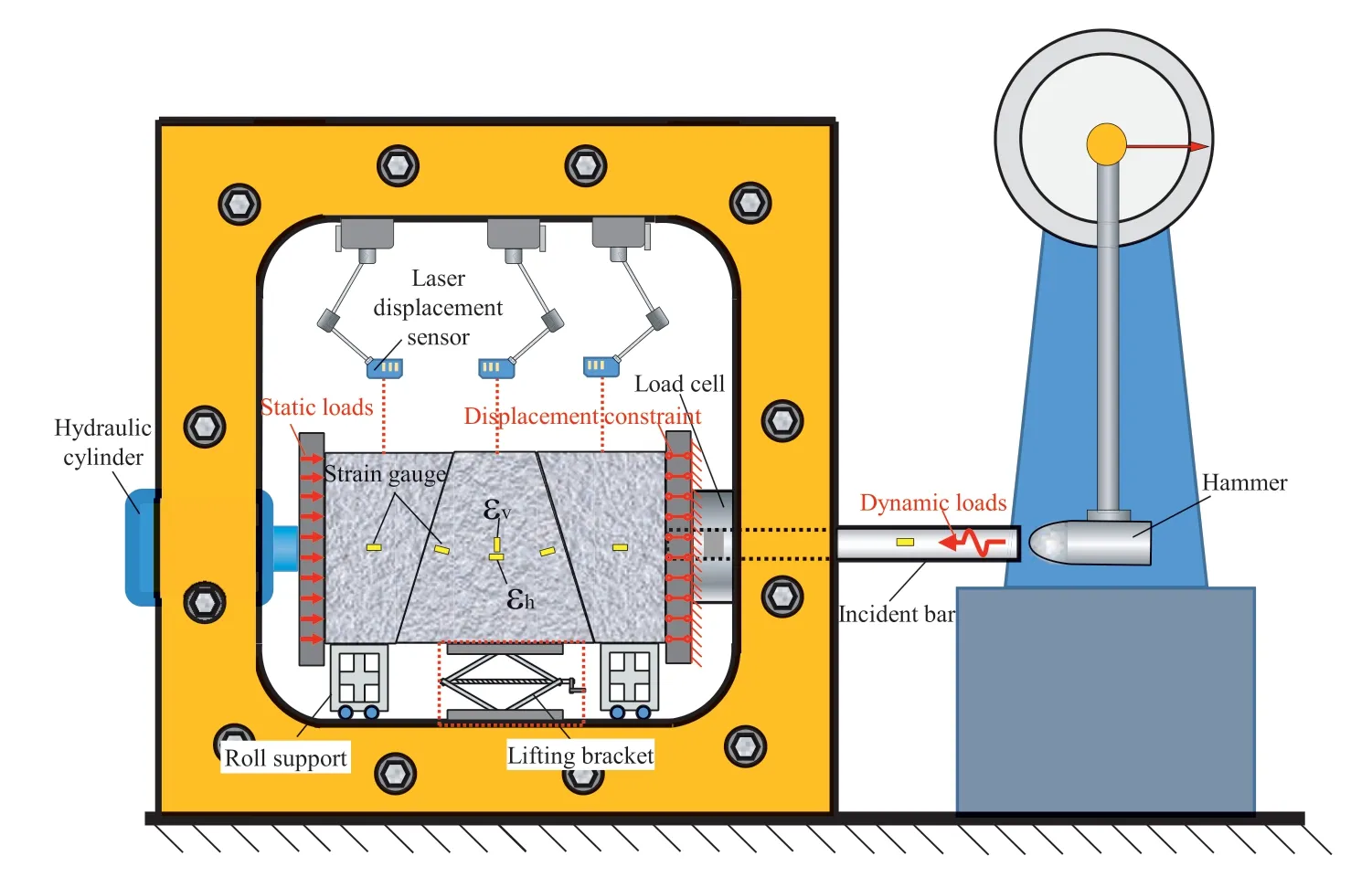
Fig.4.Schematic diagram of test device and boundary conditions of the sample.
(1) Put the left and right rock blocks on the horizontal slide-able supports,respectively.
(2) Lift the middle key block by a lifting bracket(i.e.the device in the red dotted frame in Fig.4) to fit with the bi-side rock blocks.
(3) Apply the clamping load on the block system by a hydraulic cylinder to the predetermined level.
(4) Remove the lifting bracket to suspend the key block.
(5) Pass the incident bar through the reserved hole on the side of the loading chamber and contact the right surface of the sample,then lift and release the swing hammer from a predetermined height to impact the incident bar.
As depicted in Fig.4,load sensors,laser displacement meters,high-speed cameras,and strain gages were utilized to monitor the transverse load,vertical displacement,deformation field of block’s front surface,and dynamic strain of rock blocks during the rock block disturbed sliding process.
2.3.Experimental results
2.3.1.Sliding displacement curve of key block
Under the lateral dynamic disturbance,the middle key block may lose stability and fall or restore its stable state after sliding,depending on the initial clamping load and disturbance energy.The typical sliding displacement curves for the scenario of the key block recovering to stability after sliding are depicted in Fig.5.They exhibit the following noticeable common features:

Fig.5.Typical sliding displacement curves of key block in the case of recovery stability under initial clamping loads of (a) 3 kN and (b) 5 kN.
(1) The lateral dynamic disturbance will cause an irreversible sliding displacement of the key block,which increases with the disturbance energy.
(2) The key block sliding displacement curve fluctuates with the rising wave crest rather than increasing monotonically.Generally,it reaches the peak value after two wave periods.
(3) Before an obvious macroscale displacement,the displacement curve occurred with a “slightly concave” change feature (shown in the red dotted area of Fig.5),indicating that the key block had a short and slight jitter prior to macroscale sliding.
It is also found that the sliding displacement curves of the key block exhibit two distinct development tendencies under different disturbance energy levels.Under the initial clamping load of 5 kN,when the impact energy is at a low level (i.e.4.68 J,9.03 J and 19.72 J),the sliding displacement curves of the key block are relatively consistent,exhibiting a changing trend of“linearly rise,then slightly decrease,then rise to the peak value,and finally fluctuate around the peak value and gradually attenuate”,as shown in Fig.6a.As shown in Fig.6b,when the impact energy is at a high level(i.e.32.83 J,47.78 J and 65.19 J),the key block sliding displacement curves follow the pattern of“linearly rise,then decline to near zero,then rise to the peak value,and finally fluctuate around the peak value and gradually attenuate”.Moreover,it can be observed that when the impact energy level is high,the fluctuation period of the displacement curve is significantly greater than that when the impact energy level is low.For instance,the intervals between the first two peaks of the sliding displacement curve with impact energy levels of 65.19 J and 4.68 J are approximately 0.0272 s and 0.0088 s,respectively.

Fig.6.Sliding displacement curves of the key block under different disturbance energy levels: (a) Low-level disturbance energy,and (b) High-level disturbance energy.
Fig.7 depicts the typical sliding displacement curve for the scenario of a key block falling after being disturbed,and there are two distinct forms of key block instability evolution processes:immediate instability and delayed instability.As illustrated in Fig.7a,the sliding displacement curve of the key block exhibits continuous acceleration features for the first type of disturbed instability,indicating that the key block loses its stability and falls soon after being disturbed.For the second type of disturbed instability,the sliding displacement curve of the key block shows a changing trend of “slowly rise first,then temporarily maintain stable,and finally sharply rise”,indicating that the falling of the key block is delayed for a period (about 0.1 s) after being disturbed,as shown in Fig.7b.

Fig.7.Two different types of disturbed instability processes: (a) Immediate instability,and (b) Delayed instability.
2.3.2.Deformation response of rock blocks
(1) Front surface deformation of rock block
During the sliding process of the key block,a high-speed camera with a shooting frequency of 20,000 frames per second is employed.Then,the digital image correlation (DIC) method is utilized to evaluate the deformation of the front surface.Since the DIC method can only analyze the deformation in horizontal or vertical direction,the monitored picture is rotated (as shown in Fig.8a) to maintain the contact interface vertically to assess the normal deformation near the interface.
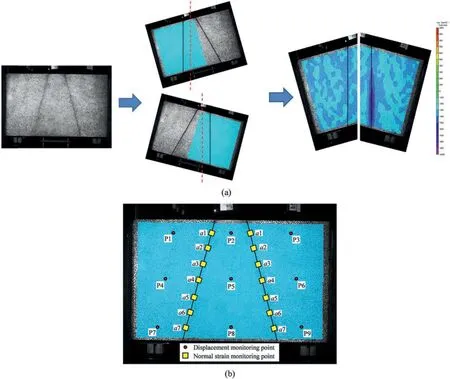
Fig.8.(a) Analysis procedure of normal strain near the interface and (b) distribution of monitoring site.
For an initial clamping load of 3 kN and lateral impact energy of 19.72 J,the horizontal displacement,vertical displacement,and horizontal strain of the front surface are extracted,as shown in Fig.9.As demonstrated in Fig.9a,when the right block is impacted by the incident bar,the middle area deforms first,and then gradually propagates to the top and bottom regions.When propagating to the central key block,the middle region of the key block is first distorted,followed by the top and bottom regions.Conversely,when the deformation reaches the left block,it first deforms in the top and bottom regions and then extends to the central region.As shown in Fig.9b,there is no significant vertical sliding displacement produced during the first time leftwards propagation of the stress wave in the rock block system.Instead,there are some incompatible deformations around the contact interface,indicating that the stress wave propagation causes the rotation of blocks.As shown in Fig.9c,compressive strain firstly appears near the bottom area of the right interface when the stress wave arrives,indicating an increase in contact conditions of this interface.After that,the normal strain near the left interface also exhibits a compressive strain zone.The compressive strain of the left interface continues to grow while the compressive strain of the right interface progressively decreases.

Fig.9.Deformation response of block surface under lateral impact disturbance: (a) Horizontal displacement field (0-0.0004 s),(b) Vertical displacement field (0-0.0004 s),(c)Horizontal strain near the interface(0-0.0004 s),(d)Horizontal displacement field(0-0.04 s),(e)Vertical displacement field(0-0.04 s),and(f)Horizontal strain near the interface(0-0.04 s).
As shown in Fig.9d,the lateral displacement of blocks changes periodically.For example,at 0.01 s,0.02 s and 0.03 s,the lateral displacement shows the same distribution,indicating that the block system regularly extrudes to the left or right during the key block sliding process.After the key block reaches its maximum displacement (about 0.03 s later),the block system provides the displacement distribution of rightward squeezing.In addition,as shown in Fig.9e,the key block does not slide down horizontally but shows a slight deflection during the sliding process.As shown in Fig.9f,the left contact interface of the key block is loosened at some time (i.e.at 0.05 s),and the right contact interface is loosened at another time (i.e.at 0.015 s),during the propagation of the lateral stress wave in the block system.The looseness and tightness of the contact interface on both sides of the key block are not synchronized,which results in an intermittent left or right rotation for the sliding process of the key block.
(2) Displacement and strain at specific locations of the block
To quantitatively analyze the contact degree of the interface,the displacement and strain responses at specific locations (as shown in Fig.8b) are extracted.As shown in Fig.10a (moving right is positive,moving left is negative),their horizontal displacement curves all demonstrate the change features of harmonic waves with gradually decreasing amplitudes.However,the amplitudes of the first wave trough of these curves present a feature of“left rock(P1,P4 and P7) Fig.10.DIC results of the key block under the condition of disturbed sliding without instability:(a)Horizontal displacement of monitoring points,and(b)Vertical displacement of monitoring points. As shown in Fig.10b(upward is positive,downward is negative),the vertical displacement curves all show the change characteristics of fluctuating decline.During the first disturbed phase of the block system,the left block went upward (i.e.the curves of P1,P4 and P7 rise) while the key block and the right block moved downward (i.e.the curves of P2,P5,P8,P3,P6 and P9 decrease).It demonstrates that the left interface slips first during the early phase of disturbance,whereas the right interface has not yet slipped.After that,the vertical displacement of the right block(P3,P6 and P9) and the key block (P2,P5 and P8) began to appear difference.Finally,the key block exhibits a relative sliding displacement with the left and right blocks. As shown in Fig.11a,when the right and left interfaces are under compression at the first stage,the horizontal displacement of the key block decreases linearly,while the vertical displacement curves of the key block exhibit a noticeable upward variation.Then,due to the reflection of the stress wave,the right interface shows a tensile strain,whereas the left interface does not (the tension state is relative to the initial state,and the interface may still be in the extrusion contact).Meanwhile,the lateral displacement of the key block continues to decrease,and the vertical displacement curve shows a clear stage of stability.After that,when the strain of the left interface also becomes tensile,the horizontal displacement curve of the key block drops to its minimum value,and the vertical displacement curve begins to decline nearly linearly. Fig.11.Normal strain at interfaces and displacement of the key block: (a) 0.001-0.008 s after lateral disturbance,and (b) 0-0.05 s after lateral disturbance. As depicted in Fig.11b,when the key block starts to slide,its horizontal displacement curve fluctuates consistently with the fluctuation of normal strain on the left and right interfaces(i.e.the interval time of the blue dotted line in the figure).It implies that the propagation of stress waves will result in the periodic extrusion of the block system,the periodic horizontal displacement of the key block,and the intermittent compression of the interface.As the horizontal displacement of the key block fluctuates,the vertical displacement curve of the key block exhibits an intermittent and progressive drop.However,the change period of the vertical displacement curve of the key block is approximately 0.001 s later than the horizontal displacement response(i.e.the red dotted line in the figure),which may be caused by the hysteresis of interface sliding response. 2.3.3.Influences of initial clamping load and disturbance energy After a dynamic disturbance,the key block may slide to lose stability or slide to restore stability.For the stability restored cases,the sliding distance of the key block increases linearly as disturbance energy rises,and the fitting coefficientR2is greater than 0.88(as shown in Fig.12a).In addition,the increase of the initial clamping load significantly raises the increasing slope of the sliding displacement of key block.As shown in Fig.12b,when the disturbance energy is constant,the disturbed sliding distance of the key block decreases exponentially as the initial clamping load increases,and the fitting coefficientR2exceeds 0.89. Fig.12.Sliding displacement of the key block under different loads and disturbance: (a) Effect of disturbance energy,and (b) Effect of clamping load. For the instability cases,the critical disturbance energy to cause the instability of the key block is statistically analyzed.With the lateral clamping force rises,the critical disturbance energy that triggers the instability and falling of the key block grows exponentially,as shown in Fig.13. Fig.13.Critical disturbance energy to induce the instability of key block. The response of rock blocks to the stress wave cannot be obtained effectively in laboratory tests or on-site engineering,while the numerical simulation method has unique advantages.Therefore,the numerical method can intuitively analyze the propagation of stress waves in the block system to reveal the mechanism of disturbed sliding of key blocks. A 3D numerical model is developed to reproduce the real experimental settings.The dimensions and materials of the numerical models such as rock blocks,baffles,incident bar,and pendulum hammer are all set according to the laboratory condition.Meanwhile,some unique designs in the experiments are adopted in the numerical simulations.For example,a reserved hole is arranged in the center of the right fixed baffle,so that the lateral incident bar can pass through it and directly contact the right rock block surface.However,in order to improve the calculating efficiency and simplify the falling process,the beginning location of the hammer is adjusted to be extremely near to the incident bar(i.e.0.001 m).Then,an initial velocityv0(v0is calculated from the actual drop height of the hammer)is applied to the hammer to impact the incident bar.Thus,it is possible to replicate the dropping of the hammer and the collision with the incident bar.Significantly,the size of the element in this numerical model is limited to less than ΔL(ΔL=λ/10-λ/8,where λ is the wavelength of the disturbance wave) to ensure the effective simulation of the stress wave propagation.The 3D model and the boundary conditions are depicted in Fig.14. The numerical computation process is divided into two stages.The first stage is to apply the lateral static load to the rock block system.Firstly,a uniform horizontal load is applied to the left surface of the left loading plate,and a horizontal displacement constraint is applied to the right surface of the right loading plate.Then,the vertical displacement constraint is removed from the bottom surface of the key block and the computation is performed until the model converges.The second stage is to apply the dynamic disturbance to the block system.The initial velocityv0of the hammer is applied to moving the hammer and hitting the incident bar.Then,a stress wave is produced in the incident bar and propagates to the rock block system. The hammer,incident bar,loading plates and supports are made of#45 carbon steel;hence an elastic constitutive model is utilized.Since the block fragments are composed of sandstone,the Mohr-Coulomb constitutive model is utilized.Table 3 lists the basic mechanical parameters of these materials,with sandstone parameters selected based on laboratory tests and steel parameters provided by the manufacturer. Table 3 Mechanical parameters of steel and sandstone. Contact elements (i.e.interfaces) are set between any two contact objects.The force response of the contact interface obeys the Hertz contact theory,and its friction-slip characteristic obeys the classical linear Coulomb friction criterion.The contact mechanical parameters between rock blocks are selected according to the direct shear test results of standard-size square specimens.It can be seen from Table 2 that the contact interface roughness of S-3 group samples is close to the trapezoidal rock block,hence its contact mechanical parameters can approximately quantify the contact property of trapezoidal rock blocks.The contact mechanical parameters of the interfaces between the hammer,incident bar,and right rock block cannot be measured directly through experiments.Instead,a trial-and-error method based on the comparison of the obtained stress wave with experimental results is used to adjust the parameters.The mechanical parameters of interface element used in the numerical analysis are listed in Table 4. Table 4 Contact mechanical parameters of interface. Consistent with the laboratory test circumstances,the dynamic disturbance is created in the numerical simulation by striking the incident bar with the pendulum,and a monitoring point is positioned 0.7 m from the impact end of the incident bar.Fig.15 depicts the axial stress wave acquired by numerical modeling and laboratory testing in the incident bar for the initial clamping load of 2 kN and impact energy of 9.03 J.The numerical simulation findings are coincident with the experimental data,demonstrating that the numerical model can accurately represent the actual situation. Fig.15.Comparison of simulated incident stress wave and experimental results. In addition,the disturbing sliding process of the key block is simulated under the conditions of restoring stability (initial clamping load of 3 kN and impact energy of 9.03 J) and losing stability(initial clamping load of 2 kN and impact energy of 9.03 J),respectively.Fig.16a and b depicts the sliding displacement curve of the key block derived from numerical modeling and experimental testing.The numerical simulation findings are essentially compatible with the experimental data,demonstrating that the numerical model is suitable for analyzing the disturbed sliding and instability process of the key block. Fig.16.Comparison of numerical simulation results with experimental results: (a) Restoring stability after disturbance,and (b) Losing stability after disturbance. Fig.17 depicts the different response information curves of the key block throughout the disturbed sliding process under an initial clamping force of 3 kN and impact energy of 9.03 J.Except for the initial 0.01 s,the horizontal stress curves of the three rock block center points oscillate in the form of wave packets around the initial value.The normal stress of interfaces on both sides of the key block also fluctuates around the initial value with the same frequency(the wave period is about 0.01 s).It implies that there is not only the propagation of the stress wave inside the rock block but also the movement of blocks when the lateral disturbance is applied to the block system.Therefore,low-frequency,low-velocity and wave packet fluctuation mode is formed.Because of this stress wave propagation mode,the normal stress and sliding resistance on the contact interface on both sides of the key block change periodically. Fig.17.Comparison between the sliding displacement of the key block and normal stress at the interface. By analyzing the normal stress curve of the contact face on both sides and the sliding displacement curve of the key block,an interesting phenomenon was found.In the second and third wave cycles of the stress wave,the displacement curve of the key block continues to rise when the normal force of the interface on both sides is lower than a certain threshold (i.e.the blue dotted line in Fig.17),whereas the displacement curve of the key block keeps constant when the normal force of the interface on both sides is higher than the threshold.It indicates that the disturbed sliding of the key block is caused by the periodic change of the normal force at the interface,which is induced by the propagation of stress wave in the block system. The stress contour plot in Fig.18 shows the first leftward propagation of the stress wave in the block system.When the incident bar hits the right block,the compressive stress wave propagates from the middle area to the left in an arc wavefront(0-0.00003 s).When the stress wave reaches the right interface of the key block,this interface will prevent the stress wave from propagating forward.About 0.0004 s later,the stress wave with the same amplitude successfully travelled through the right interface to the middle key block (0.00009 s),with an arc wavefront and inclined propagation direction (i.e.the direction has changed to perpendicular to the right interface).When the stress wave reaches the interface on the left side of the key block,it is similarly impeded by the interface.A stress wave with the same amplitude propagates to the left block 0.00005 s later.In the left block,the stress wave first appears in the top-right corner (0.00022 s),and gradually extends to the left with a linear wavefront.When it propagates to the left loading plate,the compressive stress wave is completely reflected to a tensile stress wave.It will continue to propagate to the right and overlap with the upcoming compressive stress wave. Fig.18.Horizontal stress of blocks under lateral impact disturbance (0-0.0003 s). The stress contour plot in Fig.19 shows the back-and-forth propagation of stress wave in the block system.The horizontal stress wave propagation process in Fig.19a shows obvious periodicity;that is,the compressive stress wave and tensile stress wave appear alternately.The stress contour plot of the block system at periods of 0.02146 s,0.03296 s and 0.04446 s,for example,is consistent and reveals a wide range of tensile stress zone.In addition,the stress contour plot of the block system at 0.01571 s,0.02721 s and 0.03871 s exhibits a compressive stress buildup zone close to the right contact interface.The alternating period of the tensile and compressive stress zones is about 0.0115 s (i.e.87 Hz,much lower than 2000 Hz of incident stress wave). Fig.19.Horizontal stress and vertical displacement of blocks under lateral impact disturbance (0.01571-0.04446 s): (a) Horizontal stress contour plot of block system,and (b)Vertical displacement contour plot of block system. In addition,the key block cannot maintain a symmetrical and horizontal posture during its disturbed sliding process,as shown in Fig.19b.As indicated by the red arrow in these figures,a clear oscillation occurs during the sliding process,with the arrow’s tip representing a lower position and its tail representing a higher position. Aleksandrova et al.(2008) proposed a dynamic propagation model for the block system,in which the weak connecting medium between blocks is simplified as a Kelvin viscoelastic element and the blocks are simplified as rigid bodies.Due to the rigid assumption of the blocks in this model (i.e.the block only translates but does not rotate),it is also applicable to the trapezoidal block system,as shown in Fig.20.The parameters of this dynamic propagation model include interface elastic coefficientki,interface damping coefficientci,block massmi,external impact disturbancef(t),and the lateral displacement responsexiof thei-th rock block. Fig.20.Dynamic propagation model of the trapezoidal block system. The dynamic response of the block system can be expressed as Eq.(1) can be further transformed as Eq.(2) can be transformed into a system of first-order differential equations: The solution of Eq.(3) is as follows (Pan and Wang,2014): The relative displacement between blockiand adjacent block(i-1) can be expressed as (Pan and Wang,2014): where φi,rψr,n+1=ai,r+bi,rj,λr=αr+ωrj(αr<0),θi,r=arctan(bi,r/ai,r),ai,r,bi,r,αrand ωrare undetermined coefficients,and j is the imaginary number symbol. The relative displacement between blockiand the following block(i-1)is composed of 2ncosine periodic functions,indicating that its variation period is the least common multiple of each cosine function period.Therefore,the change period of relative displacement between two blocks is only related to the distribution matrix of the block system’s stiffness,mass,and viscosity coefficient,but independent of the external disturbance. The isosceles trapezoidal block’s stress condition in a stable state is shown in Fig.21a.In order to analyze the theoretical mechanism of the disturbed sliding process of the trapezoidal key block,the following assumptions are proposed: Fig.21.(a) Force condition of trapezoidal key block and (b) Classical friction-slip constitutive model of interface. (1) Under the effect of stress wave,the normal stress of the block’s left and right interfaces is represented as (2) The maximum static friction coefficient of the contact interface is equal to the sliding friction coefficient,and the friction-slip constitutive relationship of the interface is expressed as where τ,τd,kand δdare the tangential stress,the tangential stress under sliding state,the tangential stiffness,and the critical sliding displacement of the interface,respectively. (3) The shear stress on the contact interface is uniformly distributed,which can be expressed as whereTs,τs,σsand μsare the tangential force,average tangential stress,average normal stress,and friction coefficient at the interface during the static state,respectively;Td,τd,σdand μdare the tangential force,average tangential stress,average normal stress,and friction coefficient at the interface during the sliding state,respectively;andAis the area of the interface. As the block’s weight forceGis unchanged,the slip traction forcePof block stays unaltered.However,when the stress wave propagates,the normal stress and sliding resistance at the block’s interface fluctuate.When the maximum static friction force (i.e.sliding resistance)on the interface is less than the slip traction forcePof the block,the block starts to slide(as the τ*shown in Fig.21b).For a block under the sliding circumstance,when the maximum static friction force of the interface is larger than the sliding traction force owing to an increase in normal stress,the resulting force will cause the block to slow down,or even halt (as the τ′shown in Fig.21b). Prior to being perturbed by an external dynamic disturbance,the key block was exposed to gravity and interfaced friction,with an initial shear deformation of the contact interface produced.Due to the propagation of stress wave in the block system,the normal force of the contact interface will vary.At some point,when the sliding force exceeds the maximum static friction force,the key block will slide.However,its sliding process will skip the shear deformation stage and instantly reach the macroscale sliding stage. Therefore,the motion state of the key block can be divided into three different situations: (1) When the block is initially in an equilibrium condition (i.e.v=0),the sliding criterion of the key block caused by the reduction of the normal force of the interface is as follows: At this time,the initial acceleration of the block is as follows: (2) When the block is sliding (i.e.v>0),the maximum friction may exceed the slip traction force of the key block due to the increase in normal stress of the interface.At this point,the block has an upward acceleration and decelerates till stopping (i.e.v=0).In this case,the acceleration continues to satisfy Eq.(10),but its value is negative. (3) When the block is in the stop state after sliding (i.e.v=0),even if the normal interface stress increases,the maximum static friction force will not be greater than the sliding force caused by block gravity.The key block will continue to be force-balanced and stay static.In this case,the block’s acceleration no longer satisfies Eq.(10),and its value becomes 0. Therefore,when the block is subjected to a changing normal stress on the contact interface,the acceleration of the block can be expressed as the following piecewise function (downwards is positive): Transform Eq.(10) in the form of a differential equation as follows: During this process,the development law of key block sliding displacement is dependent on the change law of normal stress on the interface.Assume that the normal force on the interface at both sides of the key block fluctuates harmonically and attenuates gradually under the influence of the stress wave propagation in the block system. The normal force on the right interface near the incident end can be expressed as The normal force on the left interface far from the incident end can be expressed as where σ0is the normal stress(Pa)on the interface under the initial in situ stress condition,determined by the lateral static load;σpis the maximum amplitude of normal stress fluctuation (Pa) on the interface caused by dynamic disturbance,determined by transverse impact energy;η is the attenuation coefficient of stress wave;ω is the parameter to determine stress wave fluctuation period;θ is the parameter to determine the initial phase of the stress wave;and Δtis the time difference of the stress wave propagating from the left interface to the right interface (i.e.Δt=ΔL/C0,where ΔLis the transverse width of the block andC0is the propagation velocity of the stress wave in the complete rock). Theoretically,when the stress wave is completely attenuated in the block system,the normal stress on the left and right interfaces should be equal,i.e.==σ0=F0/A.Introducing Eqs.(14)and (15) into Eq.(13) results in following equation: Then,the sliding acceleration of the key block can be expressed as By integration of Eq.(17),the sliding velocity of the key block can be expressed as By double integration of Eq.(17),the sliding displacement of the key block can be expressed as Since at the initial time (t0=0),the velocity v(t0)and displacement δ(t0)of the key block are both 0,it can be obtained that The mechanical parameters of the contact interface between blocks(such as stiffness coefficientkand viscosity coefficientc)are extracted from Pan and Wang(2014).The characteristic parameters of the stress wave (such as σ0,σlp,σrp,η,ω,θl,and θr) are taken by reference to the numerical simulation results.According to the theoretical analysis presented in Sections 4.1 and 4.2 of the trapezoidal key block sliding process under the influence of a lateral disturbance,the relative lateral displacement between blocks and the key block’s vertical displacement can be calculated. Fig.22a (initial clamping load of 5 kN and impact energy of 32.82 J)indicates that for the relative lateral displacement between the left block and the middle block,the fluctuation period of the theoretical results and the observed data in the first two cycles are nearly identical.However,the fluctuation period of the test results gradually increases with time after the third cycle,which may be caused by the sliding of the trapezoidal key block and the reduction of the normal force at the interface on both sides,whereas the conventional theoretical model does not account for this. Fig.22.Comparing the theoretical calculation results with experimental and numerical simulation results: (a) Lateral relative displacement between the left block and middle key block,(b) Sliding displacement under restoring stability,and (c) Sliding displacement under losing stability. Fig.22b (initial clamping load of 3 kN and impact energy of 9.03 J) demonstrates that,for the vertical displacement of the key block in the case of restoring stability after disturbance,the theoretical results are highly consistent with the experimental results and the numerical results,exhibiting an obvious stepwise upward characteristic and remaining nearly constant after reaching the maximum value during the second cycle.Meanwhile,it can be seen from Fig.22c (initial clamping load of 2 kN and impact energy of 9.03 J) that,for the vertical displacement of key block under the case of losing stability after disturbed,the theoretical results are also highly consistent with the measured results and numerical results,showing a trend of “gradually accelerating after a slightly rising". In conclusion,the theoretical calculation method of relative displacement between blocks and sliding displacement of the key block described in this research is trustworthy when a lateral dynamic disturbance is applied to a trapezoidal block system. According to the above analysis,the stress waves caused by external dynamic disturbance and propagating in the rock block system are the essential reasons for the slip and instability of the key block.The stress wave must possess some unique characteristics to effectively affect the stability of the key block.These characteristics can be obtained by analyzing the acceleration response of the center point monitored in the experiments.In addition,conventional research on pendulum-type wave theory limits the energy range of incident disturbance,hence it is necessary to explore the impact of high-energy disturbance(i.e.beyond this energy limitation) on the rock block system. 5.1.1.Propagation velocity As shown in Fig.23a,when the clamping stress is fixed,the propagation velocity of the stress wave remains unchanged with the increase of disturbance energy.As shown in Fig.23b,when the clamping stress gradually increases,the average propagation velocity of the stress wave under different disturbance energy levels increases logarithmically with the clamping load and gradually tends to the limit value.It indicates that the increase in disturbance energy will not affect the low-velocity feature of the stress wave in a block system.However,the clamping load may significantly affect the propagation velocity.When the clamping stress exceeds a specific threshold,the stress wave propagation velocity in the block system approaches that in a continuous medium. Fig.23.Propagation velocity of the stress wave under different clamping loads and disturbance energy levels: (a) Variation with disturbance energy,and (b) Variation with clamping load. 5.1.2.Vibration frequency The frequency spectrum of these block’s lateral acceleration was analyzed,and the main vibration range was represented by gravity frequency.As shown in Fig.24(the clamping load is fixed in 3 kN),although the gravity frequencies of the three rock blocks increase slightly with the disturbance energy,the difference between the gravity frequencies of the right and left rock blocks remains constant (i.e.about 800-1000 Hz).It indicates that an increase in disturbance energy will not alter the low-frequency characteristic of stress waves in a block system,i.e.the characteristic of decreasing vibration frequency with passing through rock blocks(Wang and Pan,2013).It is consistent with Wu et al.(2009)’s conclusion that “impact energy only changes the spectral amplitude of acceleration,but has no effect on the extremum frequency distribution". Fig.24.The gravity frequency of three rock block’s lateral acceleration vibration under different disturbance energy levels: (a) Gravity frequency of three blocks,(b) Frequency difference of right block and left block,and (c) Frequency spectrum of three rock block’s lateral acceleration. In addition,it can be seen from Fig.24c that,as the stress wave propagates from right to left in the rock block system,the highfrequency component of the incident stress wave in the right rock block (i.e.the grey shaded part in Fig.24c) is filtered out,resulting in the vibration frequency of the middle key block and the left rock block remaining in the low-frequency range. 5.1.3.Injected energy Kurlenya et al.(1996a,b) proposed a dimensionless energy coefficient (k=aU0/()=θ× 10-β) to judge the occurrence of pendulum-type waves in deep rock mass.Most conventional block system disturbance experiments (such as pendulum-type wave theory researches)limit the disturbance energy within this energy criterion. In this experiment,there is no limit to the energy of incident disturbance.As shown in Fig.25,only when the impact energy(i.e.the potential energy of the hammer)is 0.45 J,the energy coefficient can satisfy the energy criterion of the pendulum-type wave(i.e.thekvalue within the range of 3.55×10-11-3.79×10-9).Although the disturbance energy in most of these experiments is higher than the energy criterion proposed by Kurlenya et al.(1996a,b),they still can generate low-velocity and low-frequency fluctuations in the rock block system and induce the sliding of the key block. Fig.25.The energy coefficient k of the injected energy in the rock block system under different clamping loads and disturbance energy levels. In summary,the stress waves that cause key block slip and instability usually possess low-frequency and low-velocity characteristics,which hardly change with an increase in disturbance energy but change with the increase of clamping load. Because of its low-frequency and low-velocity characteristics,the stress wave in the block system is more likely to cause the low friction effect of the contact interface than that in the continuous medium.When the tensile phase of a low-frequency and lowvelocity stress wave hits the contact interface between blocks,it will remain in a state of looseness (or even separation) for a relatively long period of time,allowing sufficient time for the rock block to slide.The tensile phase of high-velocity and highfrequency stress waves in continuous media or analogous continuous medium may also cause the contact interface to loosen (or separate)for a very short time,but it cannot make any macroscopic response in such a brief time to affect the stability of rock block. Under the influence of low-velocity and low-frequency waves,the key rock block in the middle of the rock block system would regularly move to the right and left,as shown by periodic positive and negative oscillations of relative displacement between rock blocks in the monitoring data (i.e.the pendulum-type wave).As shown in Fig.26b,when the key block travels to the left,the right contact interface opens for a relatively long period.The right part of the key block will descend due to the force of gravity,resulting in a clockwise rotation of the key block,as illustrated in Fig.26c.Similarly,when the key block moves to the right under the influence of a stress wave,the left contact interface becomes accessible.As shown in Fig.26d,the left portion of the key block will descend due to the force of gravity,and the key block will rotate counterclockwise.Overall,the key block demonstrates occasional sliding off to the left and right under the influence of low-velocity and lowfrequency waves,which is consistent with the experimental observation and numerical simulation outcome. Fig.26.The motion of the key block under the low-velocity and low-frequency wave: (a) Before disturbance,(b) Opening of right contact interface,(c) Clockwise rotation of key block,(d) Counter-clockwise rotation of key block,and (e) Key block instability when the sliding distance exceeds the critical value. Due to the trapezoidal shape of the key block in the middle,as the block gradually slides down,there will be gaps between the key block and the rock blocks on both sides,causing the rock blocks on both sides to move towards the middle and experience a decrease in clamping force.The decrease in clamping force is inevitably positively correlated with the sliding displacement of the key block.Under on-site conditions,the specific association rules between them depend on many factors such as block shape,original rock mass properties,and stress distribution,making it difficult to be quantitatively determined.When the sliding distance of the key block exceeds a specific critical value,its clamping force will also decrease to a level that cannot maintain force balance.The key block will experience continuous acceleration sliding and falls ultimately,as shown in Fig.26e. Based on the experimental results,it can be concluded that there is generally an obvious initial sliding stage before the complete instability of the key block,as shown in Fig.27.For the different clamping loads and disturbance conditions,the initial sliding displacement varies.This initial sliding displacement is caused by several initial vibrations with great amplitude of the disturbance wave. Fig.27.Sliding displacement of key block under an instability condition. When the initial sliding displacement is much smaller than the critical sliding distance (such as 5 kN-19.72 J),the key block will undergo a gradually decreasing amplitude of vibration around the equilibrium position under the action of subsequent stress waves after initial sliding,ultimately restoring stability again.When the initial sliding displacement nearly approaches the critical sliding distance (such as 2 kN-9.03 J),some small amplitude intermittent sliding will continue to occur under the action of subsequent stress waves.As the accumulated sliding distance of the key block increases,it may exceed the critical distance after a period of time,leading to the final instability of the key block,known as “delayed instability”.When the initial sliding displacement exceeds the critical sliding distance (such as 1.5 kN-1.44 J),the key block will immediately lose its ability to maintain force balance,and accelerate sliding to instability,known as “immediate instability". Therefore,the critical sliding distance of a trapezoidal key block is crucial for analyzing its disturbed stability.However,as the critical sliding distance is determined by factors such as block shape,initial clamping force level,and the evolution of clamping force with sliding distance,further exploration and research are needed to determine this critical value. In underground excavation,it is inevitable to encounter external dynamic disturbance such as stress waves from blasting operations at the stope with the same depth or transverse seismic waves from the earthquake.When a lateral dynamic disturbance is applied to the roof block system,the stress wave will propagate back and forth in the block system,resulting in periodic loosening and compaction of the rock contact surface.When the contact face between rock blocks is loose or even detached,the ultra-low friction effect (i.e.the interface friction force decreases or disappears) occurs,resulting in the sliding or instability of rock blocks under the influence of gravity or in situ stress.For example,a dynamic disturbance (the maximum vibration is 372.8 mm/s) transmitted to the adjacent Hingir Rampur coal mine in India when conducting a blasting operation in the Samleshwari mine,which caused a roof caving accident in a roadway (Singh,2002;Singh et al.,2005).A similar accident also occurred in China’s Longyun coal mine roadway(Jing et al.,2020).Furthermore,for the tunnel excavation engineering,when a liquefied petroleum gas(LPG)storage cave is excavated by the drilling-blasting method in Sydney,the excavation blasting of the advanced cutting roadway caused a shear-slip failure of the fracture-developed roof rock mass,resulting in a large number of stones falling with a caving thickness of 1.5 m(Ambrosis and Kotze,2004). This study reveals the sliding process of a trapezoidal rock block subjected to a lateral disturbance and proposes a theoretical approach for estimating relative displacement between blocks and the sliding displacement of the trapezoidal key block.It can provide some valuable theoretical guidance for the early-warning,prevention and controlling of the roof block collapse accident.On the one hand,the numerical and experimental results imply that the friction of the interface may decrease or disappear in the block system under the high-energy and low-frequency disturbance,providing a reference for further understanding the mechanism of the disturbed instability of jointed rock masses.On the other hand,the suggested calculation methods for the key block sliding displacement have been validated by the numerical and experimental results.It can be further used to calculate the disturbed sliding process of roof blocks on-site and effectively assist in stability analysis and disaster prevention. For the case of the trapezoidal roof rock block system suffering from a high-energy lateral dynamic disturbance,a series of laboratory experiments and numerical simulations were carried out to study the evolution law of key block sliding displacement and stress wave propagation law in trapezoidal rock block system in this study.Meanwhile,a systematic theoretical analysis was also conducted to establish the calculation model of relative displacement between blocks and sliding displacement of key blocks.The conclusions can be summarized as follows: (1) The trapezoidal key block in the block system may lose or regain stability after sliding under the influence of a highenergy lateral dynamic disturbance (i.e.the magnitude of energy is in J).When its stability is regained,the irreversible sliding distance of the key block rises linearly with disturbance energy and falls rapidly with the clamping load.In the case of stability loss,there are two instability modes (i.e.immediate instability and delayed instability) for different combinations of clamping load and disturbance energy. (2) The results of DIC analysis and numerical simulation demonstrate that the primary cause of the rock block sliding was the spread of stress waves inside the block system,resulting in a periodical normal force decrease of the contact interfaces.The key block will momentarily slip when the friction force generated by the interface on both sides is less than a limit value due to the decreased normal force.On the contrary,the sliding key block will slow down or even stop.Therefore,the disturbed sliding displacement of the key block shows a step-rising characteristic generally,and the movement of the key block shows a shaking feature. (3) Based on the conventional dynamic propagation model of the block system,an analytical solution is derived for the relative displacement between blocks in a trapezoidal block system.Assuming that the stress wave propagating in the block system is harmonic,a computation model for the disturbed sliding displacement of the trapezoidal key block is established.By comparing with the findings of experiment monitoring and numerical simulation,the validity of the theoretical model is confirmed,indicating that it may provide valuable theoretical support for the prevention and control of roof block caving in engineering. (4) The low-frequency and low-velocity stress waves in the rock block system are believed to be the primary cause of the friction-reducing effect of the interface.When the tensile phase of the stress wave reaches the interface,it will remain in a tensile loosening state (or even separation) for a relatively long time,providing sufficient reaction time for the rock block sliding.This perspective can give an advancing reference for exposing the mechanism of rock mass sliding and instability under dynamic disturbance. Declaration of competing interest The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper. Acknowledgments This work was financially supported by National Key Research and Development Program of China(Grant No.2022YFC2903903),National Natural Science Foundation of China(Grant No.52304132)and Yunnan Major Scientific and Technological Projects(Grant No.202202AG050014).These support is gratefully acknowledged.



3.Numerical simulation
3.1.Numerical model and parameters setup


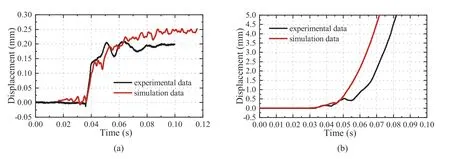
3.2.Calibration of numerical model

3.3.Numerical results



4.Theoretical analysis
4.1.Relative displacement between blocks

4.2.Sliding displacement of trapezoidal key block

4.3.Verification of the theoretical model
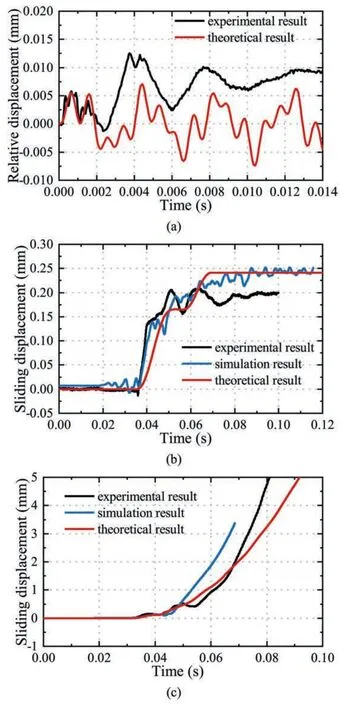
5.Discussion
5.1.Propagation characteristics of stress wave in the block system



5.2.Mechanism of key block sliding induced by lateral disturbance


5.3.Promising application
6.Conclusions
 Journal of Rock Mechanics and Geotechnical Engineering2024年3期
Journal of Rock Mechanics and Geotechnical Engineering2024年3期
- Journal of Rock Mechanics and Geotechnical Engineering的其它文章
- Using deep neural networks coupled with principal component analysis for ore production forecasting at open-pit mines
- Real-time arrival picking of rock microfracture signals based on convolutional-recurrent neural network and its engineering application
- Failure characterization of fully grouted rock bolts under triaxial testing
- Nonlinear constitutive models of rock structural plane and their applications
- Mechanical behaviors of backfill-rock composites:Physical shear test and back-analysis
- Slope stability of reclaimed coal mines through a new water filling index
