Slope stability of reclaimed coal mines through a new water filling index

Antonios Mikroutsikos,Alexndros I.Theochris,Nikolos C.Koukouzs,Ionnis E.Zevgolis

a Chemical Process &Energy Resources Institute, Centre for Research &Technology Hellas, Athens, Greece

b School of Mining and Metallurgical Engineering, National Technical University of Athens, Athens, Greece

Keywords: Post-coal era Open-pit flooding Stability charts Critical level

ABSTRACT A common reclamation practice for closed coal surface mines is filling them with water to form pit lakes.The creation and sustainability of these lakes are significantly affected by the stability of the corresponding slopes.The present study provides a general framework for analyzing the water filling’s effect on slope stability based on a new water filling index,which can indirectly consider the factors affecting the process and efficiently quantify the filling speed’s influence.The assumptions of the proposed approach are thoroughly discussed,and the range of the water filling index is identified.Furthermore,the safety factor is calculated using the finite element method with the shear strength reduction technique during the filling process for various conditions (soil properties,slope geometry,hydraulic conditions,and water filling speed).Results are presented as normalized stability charts for practical use.During the water filling,the stability gradually decreases until the reservoir reaches a critical level of 10%-40%of the total height;it then increases to even more stable conditions than the initial one.Overall,the present analysis allows for the preliminary stability evaluation of a coal mine during the formation of a pit lake and the appropriate quantification of the water filling’s effect.

1.Introduction

Several countries have pledged to cease coal-related activities during the last decade,and many surface mining areas will soon be abandoned.One of the most common reclamation practices of surface coal mines is the formation of pit lakes.This process has been applied in abandoned gold,silver,and diamond mines (e.g.Grenon et al.,2017;McCullough et al.,2020),and several pit lakes have also been formed in old coal mines(e.g.Schultze et al.,2013;Juncosa et al.,2018;Burda and Bajcar,2020;McCullough et al.,2020;Sakellari et al.,2021).

The sustainability of pit lakes is significantly affected by the stability of the slopes at the former mine boundaries.Slope failures could affect the lake’s water quality,as newly mineralized surfaces can be exposed,while pit slope failure incidents could create waves in the lake resulting in catastrophic events(Read and Stacey,2009).During the pit lake’s filling,the groundwater’s rise decreases the effective stresses and might result in failures,damaging nearby infrastructure and setting human lives at risk.

The reservoir’s water level rise has been related to the reactivation of old landslides or the provocation of new ones;this phenomenon has been thoroughly discussed mainly for dams(e.g.Yin et al.,2016;Amaral et al.,2020).Several stability problems have been reported in coal mines during water filling (e.g.Wichter,2007;Burda and Bajcar,2020),while only a few studies have examined this type of slope stability (e.g.Grenon et al.,2017;de Graaf et al.,2019;Desjardins et al.,2020).Generally,even in simplified analysis,a submerged slope’s most critical stability condition is when the submergence is partial and not when the reservoir is filled (e.g.Zevgolis et al.,2021;Kavvadas et al.,2022).

Moreover,the filling method,natural or artificial,is a controlling factor for slope stability.After the mine’s exploitation,the groundwater table’s rebound,the precipitation,and the surface runoff will eventually form a lake in the pit (natural filling).However,the pit void is usually supplied with external water sources to fill the pit rapidly(artificial filling).Diversion of rivers,water supply from nearby lakes,and water transfer from nearby active mines dewatering operations are common techniques to achieve a rapid filling and reduce the required filling period by up to 80%(de Graaf et al.,2019;Desjardins et al.,2020).This method provides several advantages;the area can be exploited faster,and better lake water quality is ensured,while it is presumed to favor stability(Schultze et al.,2011;de Graaf et al.,2019;Dahmen,2020;Desjardins et al.,2020).The role of the water filling speed on the slope stability during reservoir filling has been examined for dams(e.g.Xia et al.,2015;Yin et al.,2016)but has not been systematically quantified for pit lakes.

The present study provides a framework for investigating the water filling’s effect on slope stability.A practical approach is introduced and implemented based on a new water filling index(IWF).This index indirectly considers the factors affecting the water filling and quantifies the filling speed’s effect on stability.The assumptions of the proposed approach are thoroughly discussed,and the range ofIWFis identified.Furthermore,the safety factor is calculated during the filling process using the Finite Element Method combined with the shear strength reduction technique for various soil properties,slope geometries,hydraulic conditions,and water filling speed scenarios for typical coal mines’ slopes.The results are presented in the form of normalized stability charts for practical purposes.Overall,the present analysis allows for the appropriate quantification of the water filling’s effect and the preliminary stability evaluation of a coal mine during the formation of a pit lake.

2.Material properties and numerical method

This work uses a fundamental two-layer geomechanical model to simulate a typical lignite mine slope.The bottom layer is a bedrock-like formation with significantly higher strength and stiffness than the upper layer.This layer usually lies at the bottom of the excavation and can also sometimes be separated by a weak zone from the upper part.This two-layer concept is validated for lignite and coal mines by stability failure mechanisms;these mechanisms typically present a horizontal or sub-horizontal failure surface developing on the interface of the two layers.As a result,a composite failure mechanism (rather than a circular surface) many times represents the failure surface(e.g.Leonardos,2004;Kavvadas et al.,2020),with sliding occurring along this horizontal surface,reaching the top of the slope with a planar or curvilinear transition.This type of failure is encountered in open-pit coal and lignite mining in several countries(Ulusay et al.,2014;Bednarczyk,2017;Zevgolis et al.,2019;Ghadrdan et al.,2020;Kavvadas et al.,2020).

The development and appearance of a weak zone on that interface depend on several factors and are ignored if not specifically identified in the field.In all cases,two separate formations exist;for the purposes of the present study,the existence of a weak zone does not change the concepts of the analysis but might affect the specific quantification of the safety factor.The existence of a weak zone at the interface of the two layers,in any case,demands a specialized analysis.The upper layer can consist of various sublayers of sterile materials and coal seams;these soil formations are frequently characterized by similar shear strength (e.g.Theocharis et al.,2021),and thus,the overburden materials are herein considered a homogeneous layer.The critical parameters (e.g.Rahardjo et al.,2007;Chen et al.,2021;Mikroutsikos et al.,2021)are discussed in the following,and their range used in this work is summarized in Table 1.

Theocharis et al.(2021) presented and analyzed an extensive database with laboratory results from overburden soils from various Greek lignite (brown coal) mines.Overall,the soil’s mean effective friction angle and cohesion were 28.4°and 185 kPa,with standard deviations of 6.8°and 147 kPa,respectively;the baseline values of Table 1 are approximately one standard deviation below the mean values.The friction angle and cohesion were considered to have a broad range of 3°and 12 kPa below and above theirbaseline value,respectively,to obtain a representative range of soil properties for quantifying the overall stability.The mean value of the soil’s moist unit weight was 17.2 kN/m3in Theocharis et al.(2021) and is kept equal with that and constant given that it is a typical value for silts;the saturated unit weight was estimated to be 20 kN/m3.These values are relevant for soils’ shear strength in several other countries’ coal mines,e.g.Turkey (Tutluoglu et al.,2011),Australia (Ghadrdan et al.,2021),the Czech Republic(Vanneschi et al.,2018),and China(Hongze et al.,2020).Notice that the Young’s modulusE,Poisson’s ratio ν and the dilation angle ψ obtained typical values for numerical analysis,and their values do not affect the results of this work but are mentioned only for completeness.

The geometry of the pit lake slopes may vary significantly as it is related to the exploitation method of the former mine,the geology,and the reclamation strategy and plan.Most existing pit lakes in Germany were formed in old mines,resulting in a depth of less than 15 m (Schultze et al.,2013).However,in the last decades,surface coal excavations have often reached up to 200 m in depth(Bednarczyk,2017;Zevgolis et al.,2019) with small inclinations of 8°-14°to ensure stability (e.g.Tutluoglu et al.,2011;Bednarczyk,2017;Kavvadas et al.,2020).For instance,the former Lubstow open-pit in Poland,which has been filled since 2009,will have a maximum depth of 55 m (Burda and Bajcar,2020),while Lake Hambach in Germany,which is planned to be filled after 2050,will have a maximum depth of 170 m and slope of 11°(Dahmen,2020).Based on those considerations,the geometry of the baseline analysis was chosen as a deep slope of 100 m with a medium slope inclination of 14°.This depth was considered the largest for the analysis,with smaller depths also examined,while smaller and larger inclinations were included,as shown in Table 1.

The reservoir’s water level(L)is defined from the bottom of the excavation (Fig.1).At the beginning of the water filling,the reservoir’s level lies at the bottom of the excavation (L0=0),and it gradually rises to the final lake height,assumed to be at the slope’s crest.Steady-state flow conditions are considered for various water filling stages to simulate the groundwater evolution inside the slope.The one boundary of the steady-state flow is always the height of the pit lake,and the second is the groundwater level(Hw)at a 2Hdistance from the slope’s crest (at the left boundary of the numerical model);Hwis measured from the soil’s surface,as presented in Fig.1.

Fig.1.Simplified stratigraphy and critical parameters of a surface mine slope during water filling.

The distance 2His primarily defined on the model for the calculation of slope stability.When slope stability is calculated,the outer boundaries should be defined far enough from the crest not to affect the development of the sliding surface.The distance 2Hwas identified as appropriate for this work’s geometries and soil properties.All sliding surfaces that were examined were systematically not affected by this boundary.This distance can also be inferred as an adequate distance for most slope stability analyses,at least on similar soil properties and geometry,from similar cases in the literature (Viratjandr and Michalowski,2006;Caudal et al.,2017;Das,2021;Mikroutsikos et al.,2021).

The initial groundwater table level (Hw0) depends primarily on its depression caused during the mining process;extended dewatering typically carried around the mining area creates a cone of depression that may extend up to a few kilometers (Panilas et al.,2008;Loupasakis et al.,2014;Louloudis et al.,2022).Therefore,Hw0=0 defines a groundwater table at the soil’s surface,considering a very narrow depression cone,whileHw0=Hdefines a water table at the bottom of the excavation provoked by intense dewatering.Based on the depression cones presented in the literature and the related experience from coal and lignite mines anHw0=7.5-45 m was considered for this work covering a wide range;baseline analysis employed typical valuesHw0of 15 m and 30 m that are not too deep.

As the reservoir’s level gradually increases to reach the slope’s crest,the groundwater level also rises,i.e.asLincreases by ΔL,Hwdecreases by ΔHw(Fig.1).However,there are cases where pumping continues after the end of the exploitation,even during the water filling of the pit lakes,to hinder the groundwater table’s rebound to its pre-mining level (Schultze et al.,2011;Dahmen,2020),indicating cases where ΔHwmay be zero.Consequently,when the reservoir’s level reaches the slope’s crest,Hwcan range betweenHw0and 0 m.

This work numerically investigates the slope stability of openpit mines during the water filling using the Finite Element Method (FEM).The FEM analysis was conducted with wellestablished commercial software adapted to geotechnical engineering (Plaxis,2020) that can perform deformation and stability analysis.Two-dimensional analysis was employed with plane strain and drained conditions due to the nature of the slope stability problem examined in this work.The finite element discretization was implemented in a very fine mesh leading to approximately 5000 15-noded triangular elements,including a refinement at the area of the slope’s toe.Vertical boundaries were at 2Hfrom the slope’s crest and toe and were defined with fixed(zero) horizontal displacement.The horizontal bottom boundary was fixed in both directions (zero displacements) at depthHfrom the slope’s toe(Fig.1).All vertical and horizontal boundaries were positioned in order not to affect the analysis results.

For slope stability analysis,the FEM needs to be combined with an additional technique,the shear strength reduction;this technique is herein used with the Mohr-Coulomb failure criterion.The Strength Reduction Factor (SRF) is equal to the soil’s initial shear strength at equilibrium to the reduced shear strength at the ultimate state.It is calculated by progressively reducing the materials’shear strength to bring the slope to the verge of failure (i.e.until very large deformations or non-convergence of the solution).If φ′-c′andare the initial and the reduced parameters,then the strength reduction factor equals (Griffiths and Lane,1999):

where=c′/SRFand φ′t=arctan(tanφ′/SRF).Several researchers have stated that the above-described factor is equivalent to the well-known engineering safety factor (e.g.Griffiths and Lane,1999).As a result,the SRF calculated and identified in this work from the FEM is identical and will be used as the well-known safety factor (SF).

When employing the finite element method (FEM) for slope stability(with the shear strength reduction technique),the sliding surface arises in the form of extreme deformations.This sliding surface is a shear band,and the final result is mesh-dependent,meaning that the sliding surface’s exact location and thickness and the Safety Factor depend on the mesh density as the conventional FEM may fail to capture the strain localization accurately(e.g.Borja and Lai,2002).Several advanced methods have been proposed to address the mesh dependency problems (e.g.Tang et al.,2023);however,their application falls beyond the scope of this work.

Typically,there is a relation between the level of finite element mesh density and the accuracy of the slope stability analysis.A coarser mesh might oversimplify the geometry and soil behavior,leading to less accurate slope stability SF calculations and,often,higher SFs.On the contrary,a finer mesh can provide more detailed information about stress distributions and deformations.Nevertheless,as the mesh density increases,the results tend to be less accurate again.In this work,the results from the FEM analysis were further validated using the limit equilibrium method;the employed mesh,as decided for the reference analysis,provides identical SF and sliding surface properties for these methods.Given that the results and charts of this work are to be used for preliminary analysis,the accuracy of the FEM results is considered adequate,using a very fine FEM mesh and being identical to limit equilibrium results.

3.Development and validation of the water filling index

3.1.Definition

Pit lakes are usually filled using large amounts of water from external sources to fill the voids rapidly.It is considered that the more rapid the filling of the void,the more slope stability is favored(Schultze et al.,2011;Dahmen,2020).Nevertheless,this influence has not been systematically quantified due to the widely varying contributing factors,e.g.the climatic conditions,the permeability of the aquifers,the discharge of the external water supply,or the volume of the void(e.g.Schultze et al.,2011;de Graaf et al.,2019).

The present work proposes a framework to examine quantitatively and efficiently the direct influence of the water filling speed on the slope stability of pit lakes.When performing a stability analysis related to water filling of an excavation void,the essential information relates to the lake water and groundwater changes.All contributing factors and involved parameters contribute mainly to these two elements,the filling of the lake and the related change of the groundwater level.Following that concept,a new water filling index is introduced that considers exactly the relationship between these elements,the relationship between the groundwater level in the slope(Hw)and the reservoir’s level(L).This index is defined as the ratio of the incremental change of the groundwater level(ΔHw≥0) to the incremental change of the reservoir’s level (ΔL)during a specific period (see also Fig.1):

This ratio is dimensionless and non-negative.Very lowIWFvalues(close to zero)can be used to simulate a rapid filling process,considering that the reservoir’s level increases so rapidly that the groundwater remains practically constant.On the contrary,highIWFvalues indicate that the void’s filling is slower;thus,the groundwater has adequate time to adjust to the reservoir’s level changes.In practice,as long as the filling procedure is artificial and governed by the reservoir’s filling,IWFcannot become very large.A horizontal groundwater table that rises simultaneously with the reservoir’s level yieldsIWF=1,simulating a prolonged filling process (ΔL=ΔHw).Higher values are unrealistic except for specific scenarios.

ThroughIWF,the influence of the factors controlling the water filling speed on the slope stability is indirectly included in the change of parameters ΔLand ΔHw,and principally their ratio.Small void volumes or high discharge rates lead to the rapid increase of the reservoir’s level(large ΔL),while low aquifer permeability leads to a slow groundwater adjustment(small ΔHw);in these cases,IWFwould get values close to zero.On the contrary,large void volumes or low discharge rates indicate slower water filling(small ΔL),while high aquifer permeability leads to a rapid groundwater adjustment(large ΔHw),thus,leading to higherIWFvalues.

Notice that for this work,the groundwater level(Hw)is defined at 2Hdistance from the slope’s crest (at the left boundary of the numerical model,see Fig.1)for purposes of slope stability analysis,as explained in Section 2.In principle,the definition of the water filling index and its concept is general and can be easily adapted in other cases where a different boundary distance should be defined.However,the current definition can be used exactly as is for the purposes described in this work,i.e.water filling of open pit voids for reclamation of coal (and other similar) mines.

The water filling index offers a practical engineering approach to assess the slope stability of mines (coal,lignite and other similar)that are being reclaimed or will be reclaimed by water filling and the creation of pit lakes.Typically,during this procedure,many uncertainties exist on the geotechnical and hydrogeological parameters of the soil,the water filling speed,and the total void volume to be filled with water.These uncertainties are indirectly included in the water filling index,which includes the essence of all of them for the water filling procedure,and the relation between the water filling in the lake and in the ground.The water filling index can be used with minimal information (as many times in practice) and provide insight into the stability during mine reclamation with water filling.Its simplicity and direct engineering approach are the main reasons to use the water filling index instead of more detailed and information-needing computational and numerical procedures.

The main factors affecting the water filling index are the soil stratigraphy and permeability relating to its hydrogeological behavior,the water filling speed,and the total volume of the void to be filled with water,i.e.angles of the surrounding slopes,depth and width of the void.The advantage of the water filling index is that these factors do not need to be precisely examined for each case to calculate slope stability.A range for the water filling index can be identified based on the concepts described in the next section(section 3.2)and on the general information on the area,and based on this range,the stability can be calculated from the charts at the end of this work.This approach significantly simplifies the calculation procedure and can offer at least a preliminary assessment at a quick time and very low cost.Similar approaches have been employed in slope stability,simplifying the analysis and the parameters to obtain very fast results,for example,in the water drawdown analysis of dams(Viratjandr and Michalowski,2006).

3.2.Typical range

The challenge is to obtain the appropriateIWFrange.Transient seepage analyses focused on groundwater evolution to estimate this range for former coal mines.At the initial stage of the analysis(stage 0),steady-state flow conditions were assumed to simulate the state before the water filling.Then,the filling process was simulated considering transient state conditions,as the reservoir’s level changed with time.The filling of the whole lake was separated into four stages;for each stage,the reservoir’s level increased by ΔL=0.25H.

Some basic assumptions are needed to obtain the analysis framework.The artificial filling was considered with the external water being the only source;climatic conditions did not contribute,being insignificant compared to the external water supply.The permeability of the soil layers was 10-6m/s,a typical value for finegrained soils in coal mines (Theocharis et al.,2021).The slope’s height and inclination were 100 m and 14°,respectively,while the excavation’s shape was assumed to be a trapezoidal prism.

The width of the bottom of the excavation was 600 m and its length 1000 m,resulting in a pit volume of 100 million m3.The void was assumed to be filled with aQ=20 million m3/year discharge.These values are typical for large pit lakes and are based on three well-reported cases:lakes Most and Medard in the Czech Republic,with volumes of approximately 70 and 120 million m3filled with a maximum discharge of 20 million m3/year (Burda and Bajcar,2020);lake Meirama in Spain with a volume of 146 million m3filled with a discharge of approximately 18 million m3/year(Juncosa et al.,2018).

The effect of the pit volume on the water filling index is associated with the relation of the pit volume to the discharge rate.The same discharge rate can be high or low,referring to different void volumes.As a result,regarding the water filling index range,changing the volume is identical to changing the discharge rate as the significant element is their relation.However,one volume was assumed for the numerical analysis,as changing the discharge rate was more efficient for computational and analysis reasons.In that way,the effect of the slope angle,height and width,i.e.all affecting the void volume,is included in the final results on the range ofIWF.

The models’ boundaries were impermeable,and with this rate and pit volume,the void would be filled in 5 years.Two additional values were examined for comparison,Q=10 million m3/year andQ=5 million m3/year,that would fill the pit in 10 years and 20 years,respectively.Finally,three cases for the length of the depression cone were considered,R=700 m,1000 m,and 1500 m.Notice that the models’ vertical boundaries were extended accordingly,leading to large meshes and computational times (5-10 times larger).

The fixed water boundaries that define the flow conditions were the height of the pit lake (right boundary) and the end of the depression cone (defined as the left boundary of the numerical model).Therefore,the transient flow analysis can provide the groundwater level position at a 2Hdistance from the crest of the slope.This groundwater level is denoted byHwi,whereidenotes the number of the water filling stage,e.g.Hw0for stage 0 andHw1for stage 1.

Fig.2 illustrates the initial and the final water filling stages forR=700 m andQ=20 million m3/year.At the initial steady-state flow,Hw0=15.5 m (Fig.2a).However,the reservoir recharged the groundwater at the final filling stage,andHw4decreased to 11 m(Fig.2b).Accordingly,R=1000 m providedHw0=31.5 m andHw4=23 m,whileR=1500 m led to larger values,Hw0=45.5 m,andHw4=37 m.

Fig.2.The groundwater table for (a) the initial and (b) the final water filling stages,for R=700 m and Q=20 million m3/year.

The meanIWFcan be calculated by Eq.(2) considering ΔHw=Hw0-Hw4and ΔL=L0-L4=H=100 m and equals 0.05,0.09,and 0.09 forR=700 m,R=1000 m,andR=1500 m,respectively.However,IWFis not constant during the filling process.Fig.3 presents theIWFfor the four sequential filling stages for the transient analysis,where ΔL=0.25H=25 m for variousR(depression cone length) andQ(discharge rate) values;theIWFvaries from almost zero to 0.55.Values close to zero are observed for the first filling stage,where the reservoir’s level rises from 0 m to 25 m (L=25 m in Fig.3);this is reasonable as,in practice,the void’s filling evolves faster at the beginning due to the morphology of the pit.However,IWFincreases as the reservoir’s level rises.The maximum values are encountered when the reservoir’s level rises from 75 m to 100 m(L=100 m in Fig.3),whereIWFreaches values up to 0.55.Notice that additional analyses were conducted simulating the water filling process in more stages,and the overallIWFrange was very similar to Fig.3.

Fig.3.The water filling index IWF for four sequential filling stages,considering various depression cone lengths (R) and discharge rates (Q).

According to Fig.3,IWFis largely non-constant during the rising of the reservoir’s level for a constant inflow.Nevertheless,the water inflow(and thus,the filling speed)is rarely constant in practice;for example,water from external sources is typically not supplied during the summer.Thus,a constant value assumption for theIWFis appropriate because this work aims to examine a general framework.Thus,in the following sections,three constantIWFare systematically considered equal to 0.1,0.3,and 0.5.

4.Water filling effect on slope stability

4.1.Hydraulic conditions

This section investigates the water filling effect on slope stability through the water filling index,using the framework of the previous section.The filling process for a deep excavation slope of heightHwas split into ten stages,and the reservoir’s level increase in each stage was constant and equal to ΔL=10%H.Steady-state flow conditions were considered during each filling stage (rather than transient conditions);this assumption was employed to avoid using large models that transient analysis demands and reduce the required computational time.Moreover,combined withIWF,steady-state analysis demands fewer parameters,as transient flow analysis includes several assumptions about how the filling evolves with time,being case-specific and not necessarily more accurate.Additionally,transient flow is based on the specific period of each filling stage,while steady-state proposes a more general approach.Nevertheless,the steady-state assumption leads to a different shape for the groundwater table and differences in the pore water pressures;therefore,the differences between the two assumptions were quantified.

Various analyses were compared,simulating steady-state flow or transient conditions.Both types considered the baseline slope of 100 m in height and 14°in inclination.The effective friction angle and cohesion were φ′=22°andc′=40 kPa,the moist unit weight was 17 kN/m3,and the saturated unit weight was 20 kN/m3(Theocharis et al.,2021).Furthermore,Young’s modulus,Poisson’s ratio,and dilation angle were 20 MPa,0.3,and 0°,respectively;these values are typical for normally consolidated fine-grained soils and have a minor impact on slope stability.A non-associated flow rule with ψ=0°was employed,and the dilation’s angle impact on the stability calculations would be minor(Tschuchnigg et al.,2015).

Additionally,the bedrock’s friction angle,cohesion,and stiffness were 35°,185 kPa,and 50 MPa,respectively,and do not affect the results.Since its strength is considerably higher than the overburden soil’s parameters,the sliding surface does not cross the bedrock formation.Last,the Mohr-Coulomb elastic-perfectly plastic constitutive model was employed for the soil layers.It is standard in geotechnical engineering practice and research(Ukritchon and Keawsawasvong,2018;Pradhan and Siddique,2020) and has been systematically implemented to consider slope stability on similar occasions (e.g.Viratjandr and Michalowski,2006;Grenon et al.,2017;Wang and Griffiths,2020).Fig.1 presents the geometrical and geotechnical parameters.

For the transient analyses,Rvaried from 700 m to 1500 m,andQfrom 5 million m3/year to 20 million m3/year.The respective steady-state flow analyses were conducted considering equivalentHwvalues in each filling stage.Configurations considering steadystate flow provided similar failure mechanisms and a marginally lowerSFthan configurations considering transient seepage.The highestSFdifference between the various steady-state and transient seepage configurations was encountered forR=1500 m andQ=20 million m3/year.Fig.4 presents the shear strains that denote the failure surface position for this case.The transient analysis results in a deep groundwater level,withHw10=37 m whenL10=100 m.The respectiveSFfrom the steady-state flow analysis consideringHw10=37 m andL10=100 m is higher by approximately 5%.Notice that the steady-state flow case is always conservative with less than 5% error.

Fig.4.Shear strain contours indicating the position of the failure surfaces and SFs,considering (a) steady-state flow and (b) transient conditions.

4.2.Effect of water filling index

Various analyses were conducted considering several values for the critical parameters to investigate the role ofIWFon theSF.The analysis considered two slope heights of 50 m and 100 m and three slope angles of 12°,14°,and 16°.Seven initial groundwater conditions were simulated betweenHw0=7.5 m and 45 m,and four φ′-c′combinations were implemented,with φ′equal to 18.7°and 25.3°,andc′equal to 28 kPa and 52 kPa;overall,more than 100 analyses were carried out for eachIWF.

Fig.5 illustrates the effect of the water filling on theSFfor the various water filling stages(10 stages,as ΔL/H=10%),considering a critical combination (i.e.H=100 m,β=16°,φ′=18.7°,andc′=28 kPa)and twoHw0,at 7.5 m and 45 m.The results for all the other cases present a similar trend.The initialSF(L0=0) depends only onHw0;thus,SF=1.33 forHw0=45 m andSF=1.07 forHw0=7.5 m.A groundwater table lying closer to the soil surface(smallerHw0) provides a lowerSF.As the water filling evolves,SFdecreases until a particularL/Hvalue and then increases;further on,the lake’s reservoir plays the role of a supporting force exceeding the groundwater’s influence and,thus,SFbecomes higher than the initial one.Fig.6 presents the sliding surfaces based on the shear strains for the three stages marked with a circle in Fig.5.Notice that the figure’s legend is qualitative and not quantitative,as implementing the shear strength reduction technique results in immense,unrealistic strains that are not of interest in this analysis.

Fig.5.The safety factor(SF)versus the filling percentage(L/H)for the various Hw0 and IWF.

The value ofL/Hon whichSFbecomes minimum corresponds to the critical level and is a concept frequently encountered,especially in drawdown analysis.For cohesive soils,this level is reported to be below half of the slope height,usually aroundL=H/3 (e.g.Viratjandr and Michalowski,2006;Zhan et al.,2006;Michalowski,2009;Huang et al.,2016;Wang and Griffiths,2020;Zevgolis et al.,2021).In Fig.5,the critical level lies betweenL=20%Hand 30%H.

The results presented herein agree well with the few previous works on pit flooding.TheSFcalculations of Desjardins et al.(2020)and de Graaf et al.(2019) led to similar conclusions regarding the effect of the water filling;as the pit is filled,the water acts as a supporting force enhancing stability at the last filling stages,while the most critical conditions are encountered at the start of the process.Furthermore,Caudal et al.(2017)and Grenon et al.(2017)analyzed a case study illustrating that the failure occurred when the pit was partially filled,particularly whenL/H≈1/6 ≈17%,where the minimumSFwas encountered.Last,the evolution of theSFduring water filling presented in Grenon et al.(2017) shows a very similar evolution to the results presented in Fig.5.

Moreover,theSFs of all cases considering all the examined combinations of the critical parameters denote that the critical level’s position is strongly affected by theIWF.Fig.7a presents the relative frequency of the critical levels’position for all simulations.WhenIWF=0.1,the critical level’s position lies between 10% and 30% of the slope height,with more than 80% atL=30%H.ForIWF=0.3,the levels are in the same range,but they are distributed aroundL=30%H.Similarly,forIWF=0.5,most critical levels are also encountered atL=30%Hbut vary into a broader range,as some critical levels can also be encountered atL=40%H.Overall,for the lowIWF=0.1,the critical level’s position is lower than for the other twoIWFvalues.

Fig.7.The relative frequency of (a) the critical levels’ position and (b) the maximum SF differences for various IWF.

Additionally,Fig.7b shows the difference between the initial and the minimumSFfor eachIWF.WhenIWF=0.1,the maximum difference is 1%-7%,while it increases asIWFbecomes larger;theSFdifference forIWF=0.3 is 4%-9% and forIWF=0.5 is 5%-12%.Overall,theIWFvariation leads to an averageSFdifference of approximately 7% -lower for lowIWFand higher for highIWF-having a noticeable but not crucial effect on the stability.Thus,except for the critical level’s position,IWFalso affects theSFevolution during the water filling.

4.3.Stability charts

In slope stability,it is typical to implement the dimensionless stability factorc′/(γHtanφ′) (c′being the effective cohesion,φ′the effective friction angle,Hthe slope height,and γ the soil unit weight) in slope stability charts as it can be directly related toSF/tanφ′.This representation of stability results was initially proposed by Bell (1966) and allows for a preliminarySFevaluation without any iterative procedure.In that vein,it has frequently been used to illustrate the effect of drawdown on slope stability for the various water conditions(e.g.Viratjandr and Michalowski,2006;Wang and Griffiths,2020) and is similarly implemented in the present case.Figs.8-10 present the evolution ofSF/tanφ′during water filling,considering threeIWFvalues equal to 0.1,0.3,and 0.5,and threeHw0values,at 7.5 m,22.5 m,and 45 m,relating to depression cones from 250 m to 1500 m.The curves in each chart refer to specific water filling stages,fromL=0 toL=H.

Typical geotechnical information,the geometry of the slopes,and an estimation of the water filling index are needed to apply the following charts.This estimation can be obtained based on the previous discussions,focusing on the defined range.Usually,during the water filling procedure,stakeholders estimate the water filling speed with time,and based on this information,an engineering estimation of the water filling index is possible.Then applying stability charts(Figs.8-10)is straightforward,and the Safety Factor can be readily calculated,offering an appropriate estimation of the slopes’ safety.More detailed analysis might be necessary for areas with high risk or areas with major consequences in case of failure.However,even in these cases,a preliminary assessment can be made quickly and efficiently based on the water filling index.

Figs.8-10 denote that the critical level lies betweenL/H=0.2 and 0.4,while the most stable conditions are when the pit is filled(L/H=1).These conclusions,as well as the stability trends,agree with drawdown analysis for similar conditions.For instance,the results forIWF=0.1 in Figs.8-10 can be compared with a very slow drawdown or a drawdown considering a simultaneous alteration of the water levels in the slope and the lake (e.g.Morgenstern,1963;Viratjandr and Michalowski,2006;Lane and Griffiths,2000).However,the present results are quantitatively different due to changes in the sliding surface shape,the slope’s geometrical and geotechnical properties,and the water evolution mechanisms.

The stability charts can also be used to observe further theIWFeffect on the stability during the water filling process.The increase ofIWFfrom 0.1 to 0.5 leads to the increase of the critical level’s position fromL/H=0.2 to 0.4;this is profound in most charts(e.g.see Figs.8c,9b and 10c),where the increase ofIWFleads theL/H=0.4 curve to lowerSF/tanφ′values compared toL/H=0.2.Moreover,the increase ofIWFresults in lower stability conditions.For instance,in Fig.8c and forc′/(γHtanφ′)=0.035,ifIWF=0.1,SF/tanφ′decreases from 4.74 to a minimum of 4.48 (5% reduction)while ifIWF=0.5 minimumSF/tanφ′becomes 4.21(11%reduction),which is a noticeable effect on the slope stability.It should be noted that a groundwater table lying closer to the soil surface (smallerHw0) is less affected by theIWF;thus,a more significantIWFinfluence is observed for deeper water tables.

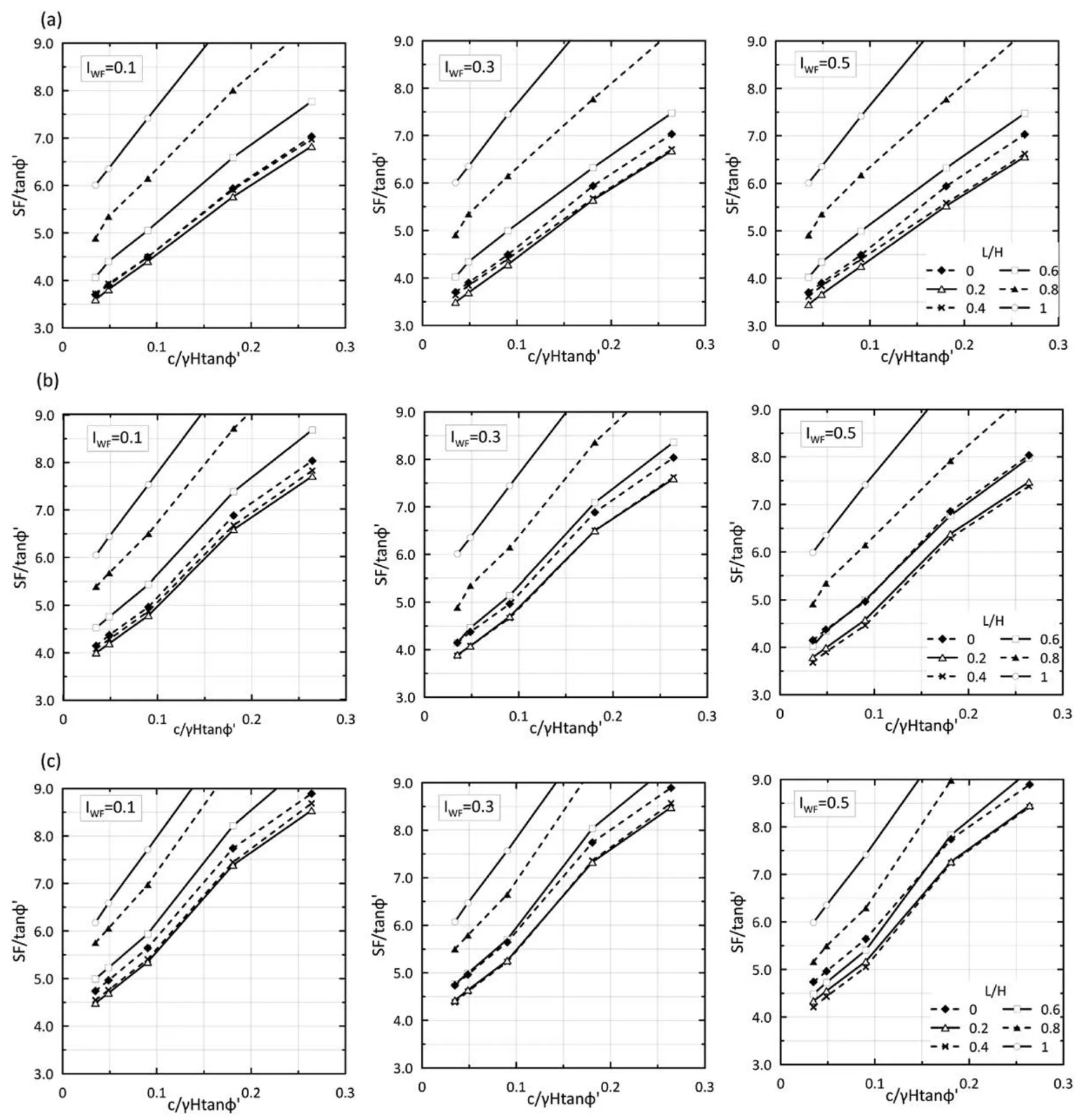
Fig.8.The evolution of SF during water filling for all stages (L/H=0-1),for (a) Hw0=7.5 m,(b) Hw0=22.5 m,and (c) Hw0=45 m,considering β=12°.

Fig.10.The evolution of SF during water filling for all stages (L/H=0-1),for (a) Hw0=7.5 m,(b) Hw0=22.5 m,and (c) Hw0=45 m,considering β=16°.

5.Conclusions

The present work investigates the effect of the water filling on the slope stability of former coal mines.An efficient and practical approach is proposed and implemented based on a new water filling index,namedIWF.The water filling index is a practical approach to assess the slope stability of reclaimed mines by pit lakes.Typically,many uncertainties exist on the geotechnical and hydrogeological parameters of the soil,the water filling speed,and the total void volume.These uncertainties are indirectly included in the water filling index,which includes the essence of all of them for the water filling procedure,and the relation between the water filling in the lake and in the ground.The water filling index can be used with minimal information (as many times in practice) and provide insight into the stability during mine reclamation with water filling.By definition,IWFis a dimensionless,non-negative number that practically varies from 0 to 1.For the stability problem of pit lakes,IWFvaries from 0.1 to 0.5.The low value of 0.1 simulates a very fast filling process,while 0.5 indicates that the void’s filling occurs at a slow rate.

A simplified two-layer stratigraphy was implemented to simulate a representative scenario for coal mines.Steady-state flow conditions were assumed during each filling stage,an assumption further examined by FEM analysis by comparing steady-state flow and transient conditions.Configurations considering steady-state flow provided similar failure mechanisms and a marginally lowerSFthan the simulations with transient seepage.Since the results were on the conservative side and the error was less than 5%,it is concluded that steady-state flow conditions can be considered for modeling and analysis purposes.

Using the proposedIWF,the water filling effect on theSFwas investigated through numerical analysis.For all scenarios,as the water filling evolves,SFdecreases to a minimum at a certain value of the ratioL/Hfor each examined case and then rises to values higher than the initialSF.These very highSFs at the final filling stages are due to the free water surface that poses an immense supporting force.The maximumSFreduction was betweenL=10%Hand 40%H,with most simulations leading to critical levels atL=20%Hand 30%H.The results presented herein also agree with the findings of the few previous works on pit flooding.The water filling’s effect on stability is also similar to drawdown,where the critical level is aroundL=H/3.

Moreover,the critical levels’position is significantly affected byIWF,indicating fast or slow filling;the faster the water filling,the lower their position is encountered.In particular,forIWF=0.1(rapid filling process),the critical levels were mostly encountered atL=20%H,while forIWF=0.3 and 0.5(slower water filling),they were aroundL=30%H.In addition,the minimumSFat the critical levels depends on theIWF;IWF=0.1 reducesSFby 1%-7%,whileIWF=0.5 causes a maximumSFdrop equal to 5%-12%.This reduction is noticeable and might be crucial in practice as mine slopes are designed with lowSFs,close to 1.1-1.2.In such cases,the rapid filling of the lake can improve the stability of the pit during flooding,while a slower filling process might lead to failure.

Safety results were presented in stability charts,implementing the dimensionless stability factorc′/(γHtanφ′).This representation offers the direct calculation of theSFbased on the slope’s geometry and geotechnical properties.The stability trends generally agree with drawdown analysis,although the present results are quantitatively different.

Overall,a general framework for investigating the water filling’s effect on slope stability was established based on a new index,IWF.This practical approach efficiently evaluates the slope stability of open-pit mines during water filling towards forming a lake,avoiding details that are possibly difficult or impossible to identify in engineering practice.Stability charts provide a practical way to evaluate slope stability based on the main parameter andIWF.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgments

This work has received funding from the European Union’s Research Fund for Coal and Steel under the projects RAFF grant agreement No.847299 and POMHAZ grant agreement No.101057326.Financial assistance by the European Commission is much appreciated.