Damage constitutive model of lunar soil simulant geopolymer under impact loading

Hanyan Wang,Qinyong Ma,*,Qianyun Wu

a School of Civil Engineering and Architecture, Anhui University of Science and Technology, Huainan, 232001, China

b Engineering Research Center of Underground Mine Construction, Ministry of Education, Anhui University of Science and Technology, Huainan, 232001, China

Keywords: Lunar soil simulant geopolymer (LSSG) Split hopkinson pressure bar (SHPB) test Constitutive model Energy analysis Failure mode

ABSTRACT Lunar base construction is a crucial component of the lunar exploration program,and considering the dynamic characteristics of lunar soil is important for moon construction.Therefore,investigating the dynamic properties of lunar soil by establishing a constitutive relationship is critical for providing a theoretical basis for its damage evolution.In this paper,a split Hopkinson pressure bar(SHPB)device was used to perform three sets of impact tests under different pressures on a lunar soil simulant geopolymer(LSSG) with sodium silicate (Na2SiO3) contents of 1%,3%,5% and 7%.The dynamic stress-strain curves,failure modes,and energy variation rules of LSSG under different pressures were obtained.The equation was modified based on the ZWT viscoelastic constitutive model and was combined with the damage variable.The damage element obeys the Weibull distribution and the constitutive equation that can describe the mechanical properties of LSSG under dynamic loading was obtained.The results demonstrate that the dynamic compressive strength of LSSG has a marked strain-rate strengthening effect.Na2SiO3 has both strengthening and deterioration effects on the dynamic compressive strength of LSSG.As Na2SiO3 grows,the dynamic compressive strength of LSSG first increases and then decreases.At a fixed air pressure,5%Na2SiO3 had the largest dynamic compressive strength,the largest incident energy,the smallest absorbed energy,and the lightest damage.The ZWT equation was modified according to the stress response properties of LSSG and the range of the SHPB strain rate to obtain the constitutive equation of the LSSG,and the model’s correctness was confirmed.

1.Introduction

With the boom in lunar exploration,an increasing number of countries are exploring lunar resources,which is a significant aspect of human society’s development (Ouyang,2004;Zheng et al.,2008a).Drilling and sampling,surface sampling,and sealing of the lunar surface for China’s Chang’e-5 spacecraft were completed on 2 December 2020,and 1731 lunar samples were obtained(Xu et al.,2018;Qian et al.,2021;Zhang et al.,2022).Space sampling is a significant step in the study of lunar soil resources.The landing of spacecraft and drilling and sampling using a sampler during lunar exploration missions will have certain dynamic effects on lunar soil (Prabu et al.,2022).The dynamic characteristics of lunar soil are crucial for future lunar base construction and should be considered in the design of lunar building load(Ghayoomi et al.,2017;Liu et al.,2020).

Because the sizes of existing lunar soil samples are insufficient for engineering tests,developing a lunar soil simulant material for engineering research is an urgent matter.The JSC series lunar soil simulants developed by the Johnson Space Center of NASA are among the earliest to be developed and applied,and its raw material is volcanic ash (Ray et al.,2010;Song et al.,2019).The strength and deformation characteristics of JSC lunar soil simulants have been measured(Taylor et al.,2016;Wang et al.,2017).Japan’s Shimizu Corporation’s Space and Robotic Systems Division has developed two lunar simulations,i.e.MKS-1 and FMK-1,based on Apollo 14 lunar soil samples.They employ basalt as the raw material,and their main purpose is to meet the needs of in situ resource utilization research on the moon (Kanamori et al.,1998;Uesugi et al.,2009).The CAS-1 lunar soil simulant developed in China employs low-titanium basaltic scoria and has scientific research significance for future moon programs (Zheng et al.,2008b).Table 1 lists the lunar soil simulants from various countries and their uses.

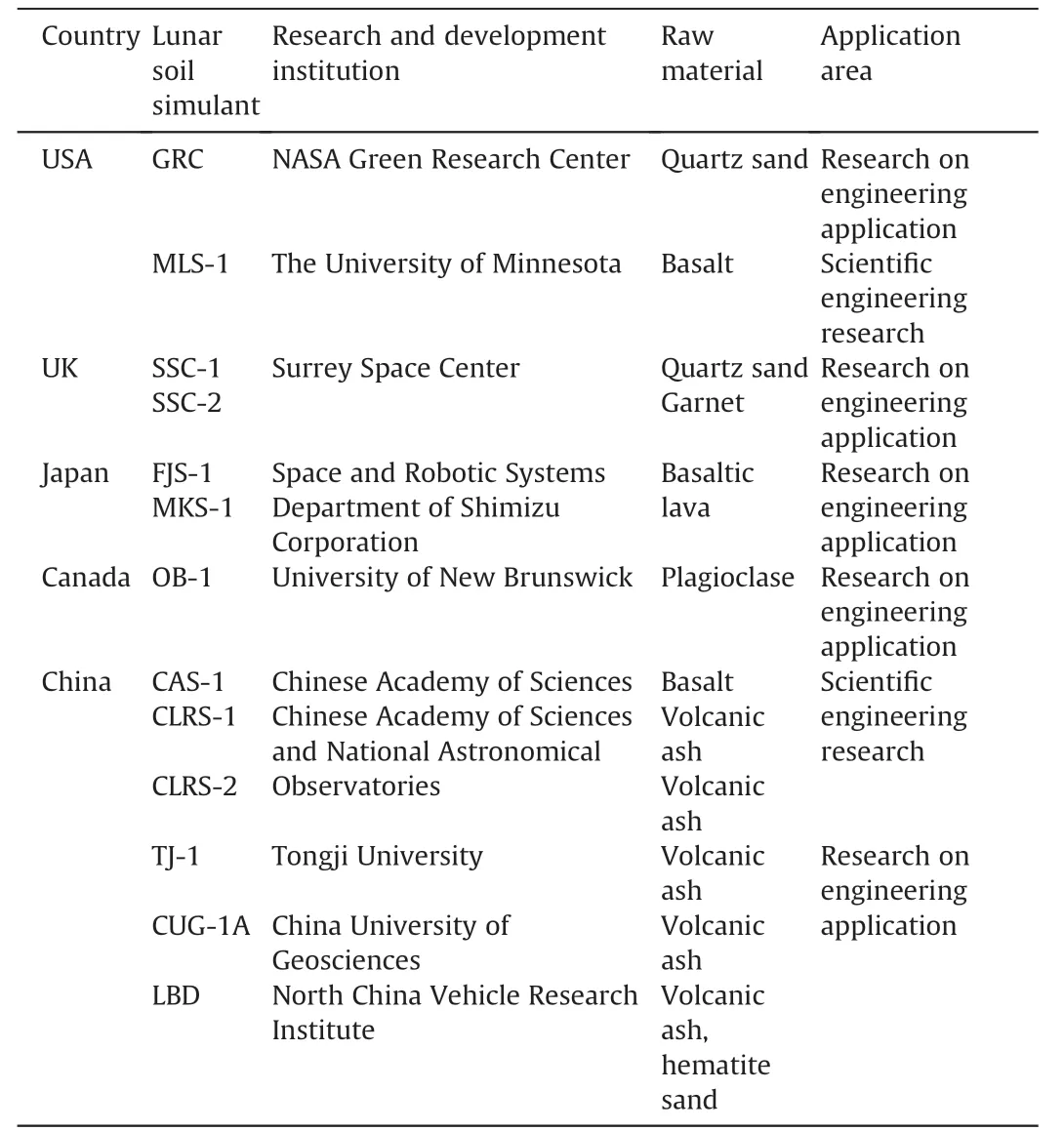
Table 1 Development of lunar soil simulant in different countries.

Lunar soil has a very low density,making it infeasible as a building or foundation material for moon construction and,thus,requires strengthening (Farries et al.,2021;Zhou et al.,2021).Alexiadis et al.(2017)used a lunar soil simulant as the raw material and NaOH as an alkali activator to prepare geopolymers with compressive strength up to 18 MPa.Geopolymers can effectively improve the strength of lunar soil simulants.At present,the literature has focused on the static mechanical properties of lunar soil simulant geopolymers(LSSGs).Montes et al.(2015)first attempted to prepare a geopolymer by using lunar soil simulant as raw material in 2015.They found that the materials with a larger specific surface area and higher content of silicon and aluminum elements were more likely to improve the strength of the geopolymer.Momi et al.(2021) studied the influences of urea and water on the mechanics and rheological properties of geopolymers in a lunar soil simulant under the action of a NaOH alkali initiator.Prabu et al.(2022) studied the dynamic characteristics of a lunar soil analog(LSS-ISAC-1) through a cyclic triaxial test and obtained its shear modulus,damping ratio,and Poisson’s ratio.However,studies on the dynamic properties of LSSG remain scarce.

Accordingly,Na2SiO3was used as an alkali activator in this study to prepare an LSSG.A split Hopkinson pressure bar(SHPB)test was performed as a uniaxial impact compression test.The effects of Na2SiO3content,curing age and impact pressure on the dynamic compressive strength of LSSG were studied.The ZWT constitutive model was simplified by considering the dynamic characteristics of LSSG,and a rate-type damage constitutive equation was derived.Additionally,a viscoelastic constitutive model with nonlinear,Maxwell and damage bodies based on the Weibull distribution was proposed and experimentally verified.

2.Test materials and equipment

2.1.Test materials

The choice of crushed basalt as a lunar soil simulant material in this experiment was informed by similarities in the material composition between basalt and lunar soil (Qian et al.,2020;Ma and Wang,2022),as shown in Fig.1 (Schleppi et al.,2019;Zarzycki and Katzer,2019;Engelschiøn et al.,2020).The collected basalt was dried,crushed,screened and ground to make the lunar soil simulant(Fig.2),and the obtained particle gradation is shown in Fig.3.The grain size of the lunar soil simulant in the literature is shown in Fig.4 (Jiang et al.,2012;Zou et al.,2016;Monkul and Dacic,2017).

Fig.1.Comparison of lunar soil mineral composition.

Fig.2.Photograph of the lunar soil simulant.

Fig.3.Particle size distribuion of the lunar soil simulant.

Fig.4.Lunar soil grain sizes present in the literature.

Dissolving sodium silicate in the water results in a colorless transparent viscous liquid with a pH value of 11-13 and a modulus of 1.2.

2.2.Design of the SHPB test

The effects of curing age(7 d and 28 d),Na2SiO3amount(1%,3%,5%and 7%),and air pressure(0.2 MPa,0.3 MPa and 0.4 MPa)on the dynamic compressive properties of LSSG were analyzed.Table 2 lists the test schemes.

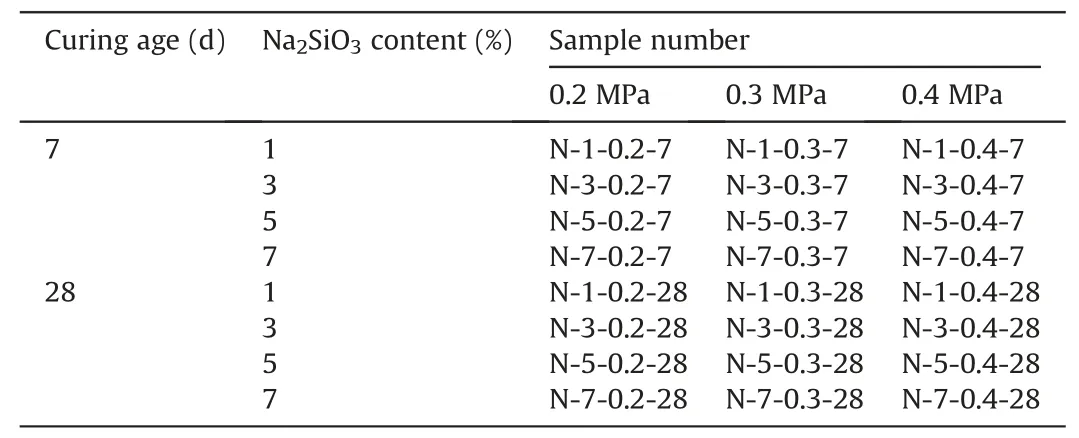
Table 2 Design of the SHPB test with different air pressures.

2.3.SHPB device

A SHPB device mainly includes power launching,pressure bar test,signal receiving and acquisition,and signal processing devices(Ma and Gao,2018).Fig.5 depicts a schematic diagram of the main device.

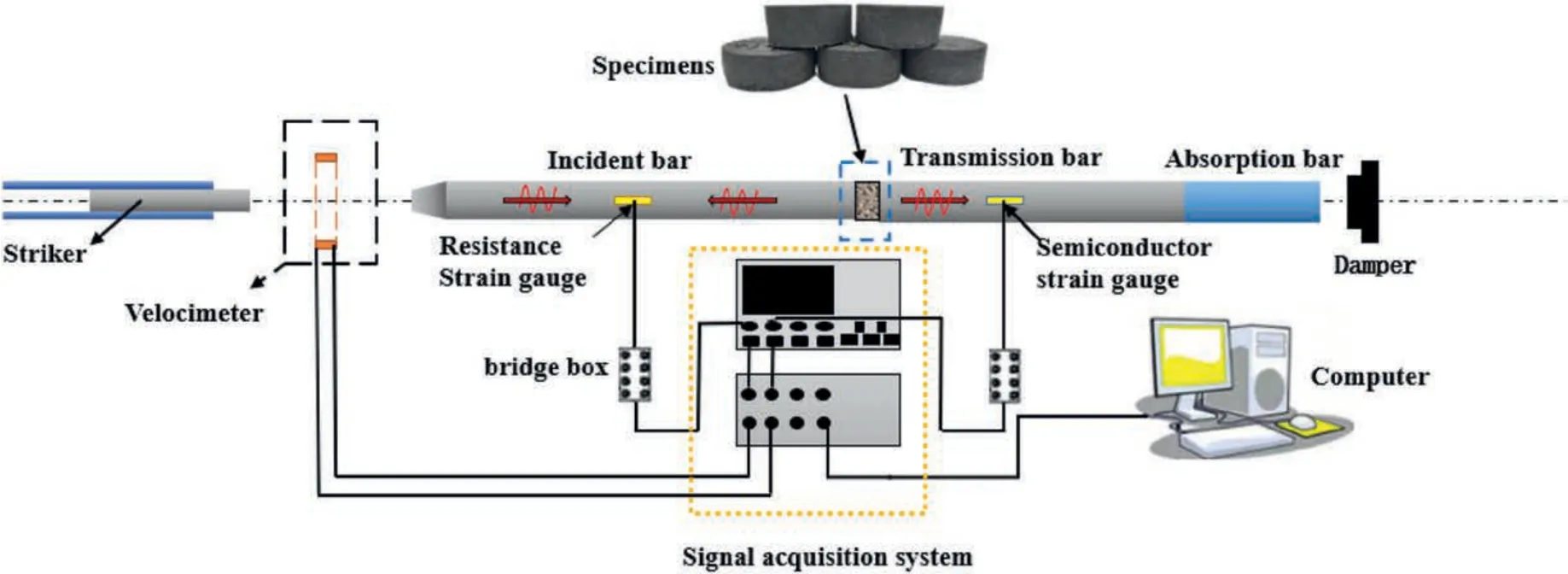
Fig.5.Schematic diagram of the SHPB test device.

The striker,incident bar,and transmission bar used in the test were all made of steel.The diameter of the pressure bar was 50 mm,and its density was 7.8 g/cm3,whereas the elastic modulus of all bars was 210 GPa.The transmission velocity of the stress wave was 5190 m/s.The stress and strain of LSSG were obtained using strain gauges fixed on the incident and transmitted bars and the signal acquisition system.Because the wave impedance of LSSG is small,a sensitivity coefficient of 110%±5%was used in the semiconductor strain gauge fixed to the transmission bar,whereas that of the resistance strain gauge on the incident bar was 2% ± 5%.

SHPB is mainly used for testing the relationship between stress and strain in materials under one-dimensional (1D) stress and strain rates of 100-1000 s-1.To satisfy some test conditions,the following assumptions are made:

(1) The transmission of a stress wave in the bar conforms to 1D stress wave theory.

(2) The inertia effect of samples can be ignored.

(3) The stress and strain in the samples are homogeneous.

(4) The friction effect of the compression surface between the sample and bar can be ignored (Xue et al.,2021;Xiao et al.,2021).

The transmission mode of the stress wave in the bar is shown in Fig.6.

Fig.6.Stress wave transmission in SHPB.

2.4.Test data processing

To ensure stress uniformity during loading in the SHPB test,all bars and specimens were adjusted before the test to ensure collinearity in the pressure bar and sample.In addition,a waveform shaper was used to reduce waveform oscillation and ensure an appropriate rise time of the incident pulse,thus effectively ensuring constant strain rate loading(Xia et al.,2008).The original waveform was obtained by smoothing the wave collected on the oscilloscope and determining the baseline,as shown in Fig.7.The stress,strain and strain rates in the samples were calculated using the three-wave-method formula from the original incident,reflected and transmitted waves collected (Song and Hu,2005).

Fig.7.Original waveform of LSSG.

Balanced stress is necessary to ensure the stress uniformity at both ends of the samples and the test accuracy.The relationships of incident,reflected,transmitted,and incident+reflected stresses with time in the pressure bars at both ends of the sample were obtained,as shown in Fig.8.

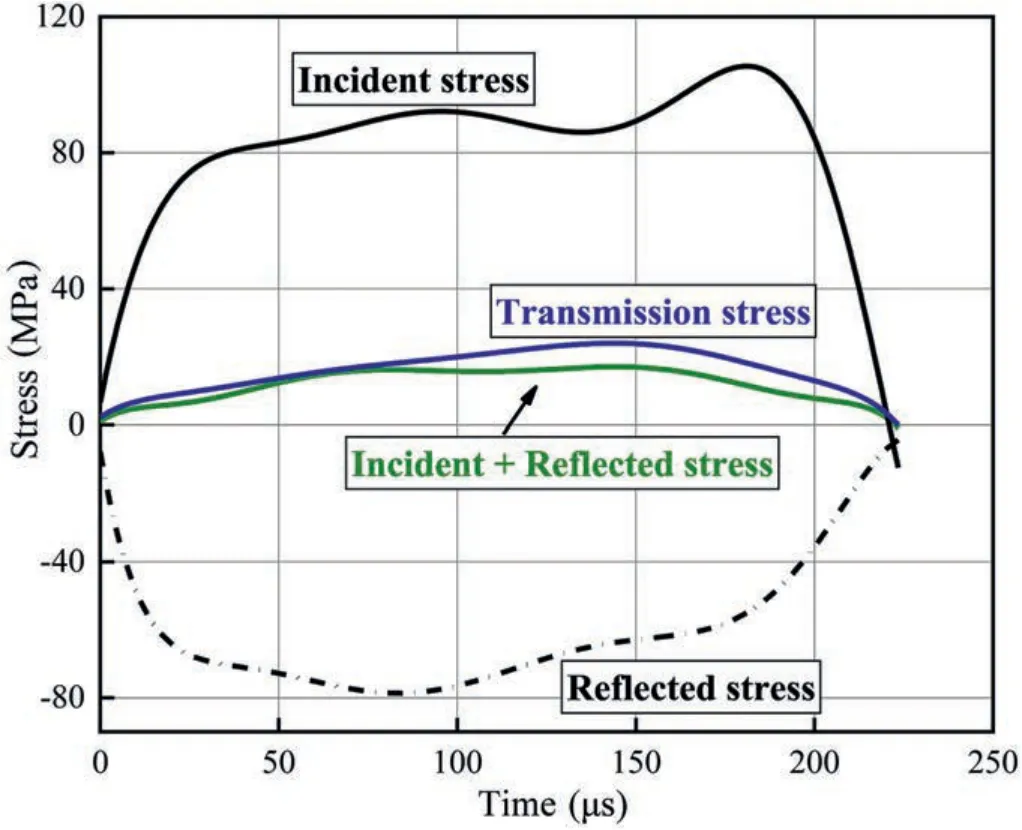
Fig.8.Verification of stress uniformity.

As shown in Fig.8,the waveforms of the transmitted wave and incident+reflected wave are very similar,which suggests that the LSSG sample reached stress equilibrium during the impact process.

Due to the large dispersion during preparation of LSSG samples,four groups of parallel samples were created in the experiment for each group of variables,the dispersion of the LSSG wave velocity was analyzed,and the coefficient of variation was determined to avoid the influence of LSSG defects and ensure the test accuracy.Notably,a larger coefficient of variation results in a greater dispersion.To meet the experimental requirements specified in GB/T23561.1-2009 (2009),a coefficient of variation less than 20% was used,as listed in Table 3.

Table 3 Experimental parameters of the lunar soil simulant.

3.Analysis of dynamic compression performance of LSSG

3.1.Dynamic stress-strain curve

3.1.1.Change in stress-strain curve of LSSG with curing age

Fig.9 shows the dynamic stress-strain curves of LSSG at a strain rate of 57.435 s-1and curing ages of 7 d and 28 d(Ma et al.,2019).As shown in Fig.9a,the linear elastic stage in the stress-strain curve is longer at the curing age of 7 d.When 1% Na2SiO3was used,a prepeak elasto-plastic plateau stage was observed in the stress-strain curve.When the Na2SiO3content was increased from 3% to 7%,the peak stress in the curve first increased and then decreased.The maximum peak stress was achieved by using 5%Na2SiO3.Compared with samples containing 1% Na2SiO3,the peak strain in the samples containing 5%Na2SiO3increased significantly,indicating that the LSSG ductility could be effectively improved by adding Na2SiO3at the early stage (Koohestani et al.,2021).

Fig.9.Dynamic stress-strain curves of LSSG at different curing ages: (a) 7 d,and (b) 28 d.

Fig.9b shows the stress-strain curve of LSSG with a curing age of 28 d.When 1% Na2SiO3was added,the stress-strain curve exhibited prominent brittle failure characteristics;specifically,before peak strength was reached,the stress increased with strain,and after peak stress was reached,the stress decreased to the residual stress with an increase in strain,at which point the samplefailed.When Na2SiO3content was increased from 3% to 7%,the stress-strain curve became steeper and “narrow,” whereas the curve shifted leftward compared to that at a curing age of 7 d.This indicates that with an increase in curing age,the ductility of LSSG decreased,and the brittle failure became more marked(Xiao et al.,2022).

3.1.2.Change in dynamic stress-strain curve of LSSG with strain rate

Fig.10 shows the changes in the dynamic compressive stressstrain curves of LSSG with strain rate.The following findings can be inferred:

Fig.10.LSSG stress-strain curves under different strain rates: (a) 1% Na2SiO3,(b) 3% Na2SiO3,(c) 5% Na2SiO3,and (d) 7% Na2SiO3.

(1) The impact dynamic peak stress of LSSG has a prominent effect on the strain rate,i.e.with increasing strain rate,the peak strength continuously increases,especially when 1%Na2SiO3is used,and the change in peak stress value is more prominent.

(2) Under different strain rates,the dynamic stress-strain curves exhibited the same general trend,which could be divided into pore closure,elastic,plastic yield,and the failure states.

(3) When the strain rate increased,the strain corresponding to the peak stress of the sample also increased,which may be attributable to the pressure increase caused by the gap inside the LSSG being unable to expand and extend over the short duration.On the other hand,the number of cracks in other areas increased,resulting in the increase in peak strain.

(4) When 5% Na2SiO3was added,the curve exhibited almost linear growth before the peak stress was reached.Moreover,the curve exhibited a cliff drop at the final failure stage,indicating that the LSSG with 5% Na2SiO3has good linearly elastic characteristics.

3.1.3.Typical stress-strain curve of LSSG

As shown in Fig.11,the dynamic stress-strain curves of LSSG exhibited similar characteristics under different curing ages and strain rates across the following stages(Gao et al.,2022;Liu and Li,2022):

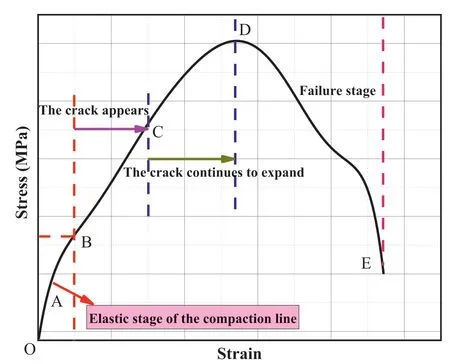
Fig.11.Typical dynamic stress-strain plot of LSSG.

(1) Grain compaction state (OA): Under impact loads,the dynamic stress-strain curve rises rapidly.The impact load results in closely spaced microcracks and improves the compressive and deformation resistance of the LSSG.

(2) Elastic state(AB):Stress and strain increase proportionately.Moreover,the stress wave in the sample reaches stress balance after several reflections.Meanwhile,the external impact load cannot create new cracks in the sample,the sample remains elastic,and the slope of the stress-strain curve remains constant.The slope at this stage is taken as the dynamic elastic modulus of the LSSG.

(3) Crack-appearance state (BC): The slope of the stress-strain curve is smaller,and the stress increases slowly with the increase in strain,changing the state of the specimen from elastic to plastic.

(4) Crack continued propagation state (CD): During this stage,the dynamic stress continues to increase,but the slope of the curve approaches zero.As the load continues to increase,the cracks in the sample expand,and the sample can still bear some load before the peak stress.

(5) Failure state (DE): After the sample reaches the peak stress,the slope of the stress-strain curve becomes negative,and the stress decreases at different rates under different air pressures.Meanwhile,the sample has fully lost its bearing capacity,and severe deformation and failure occur.

3.2.Dynamic compressive strength

The variation law of the dynamic strength of LSSG under different curing ages and Na2SiO3contents is shown in Fig.12.The following rules can be inferred:

(1) After adding Na2SiO3,the dynamic compressive strength of LSSG markedly improves.Their strengths under different curing ages exhibit the same law when the Na2SiO3content increases.It increases slowly and then decreases,and the maximum strength is reached when 5% Na2SiO3is used.

(2) With increasing curing age,the dynamic strength continuously increases.When the strain rate is 57.435 s-1,the 28 d dynamic compressive strength of the sample with 1%Na2SiO3is approximately twice as high as that of the 7 d strength.With the increase in Na2SiO3from 3% to 7%,the 28 d dynamic strength of samples increases by 24.53%,13.11%and 13.9% compared with that of the sample with 7 d of curing.

(3) When the strain rate is 82.516 s-1and the Na2SiO3content increases from 1%to 7%,the 28 d dynamic strength increases by 62.51%,30.4%,20.96% and 29.7%,compared with the 7 d dynamic strength.When the strain rate is 109.825 s-1,with the increase in Na2SiO3content from 1% to 7%,the 28 d dynamic strength of LSSG increases by 78.52%,28.7%,36% and 37.56% compared with the 7 d dynamic strength.

3.3.Variation in dynamic strength with strain rate

To study the change in the LSSG dynamic compressive strength with strain rate,the compressive strength and strain rates of samples with Na2SiO3contents of 1%,3%,5%and 7%were analyzed,as shown in Fig.13.The following rules can be derived:

Fig.13.Relationship between dynamic compressive strength and strain rate.

(1) The strain rates of all samples are in the range of 40-110 s-1.With the increase in strain rate,the dynamic compressive strength of LSSG tends to increase.

(2) The slopes of the fitted curves of the dynamic compressive strength and the average strain rate corresponding to Na2SiO3contents of 1%,3% and 5% are approximately the same.

(3) When the strain rate increases from 50 s-1to 100 s-1,the variation range of dynamic compressive strength of LSSG with 7% Na2SiO3is the largest,indicating that the dynamic compressive strength of LSSG with a higher Na2SiO3content is more strongly affected by the average strain rate.

4.Failure patterns of LSSG

The mechanism by which Na2SiO3improves the lunar soil simulant is by closely joining the particles inside the sample through Na2SiO3cementation.Inevitably,pores and microcracks will form in the internal structure.These defects also deteriorate the mechanical properties.During dynamic tests,the microcracks in the LSSG expanded under increasing impact loads,and the outer part of the samples exhibited macroscopic cracks (Li et al.,2021).The dynamic failure patterns of LSSG are shown in Fig.14.

Fig.14.Failure modes of specimens in dynamic tests.

Fig.14 shows that the Na2SiO3content greatly influences LSSG failure.The main influence rules are described as follows(Han et al.,2022;Song et al.,2022a):

(1) When 1%Na2SiO3was added and the strain rate was 54.069 s-1,the sample was broken.Moreover,the breakage was greater at a strain rate of 62.82 s-1.With the strain rate increasing up to 87.105 s-1,the LSSG sample was crushed,with almost no large fragments remaining.Therefore,with an increase in pressure,the stress wave does not rapidly pass through the existing crack area in the sample.It directly followed the shortest path through the particle,resulting in a relatively large degree of crushing.

(2) When the Na2SiO3content was 3%,the sample breakage became apparent at a strain rate of 54.297 s-1;however,this was observed in only a small portion of the samples.Withthe strain rate increasing from 78.12 s-1to 90.426 s-1,increasingly larger parts of the sample were broken.However,compared with the 1%Na2SiO3samples,the part of the test block that was broken was larger than that which was crushed.

(3) The samples with 5% Na2SiO3,unlike those with 1% and 3%Na2SiO3,maintained integrity under a strain rate of 57.435 s-1.However,only some slight cracking appeared,and the residual strength was relatively large at this time.When the strain rate was 82.516 s-1,large cracks appeared on the LSSG failure surface,and the sample was divided into two parts,which was accompanied by the appearance of small cracks.With the continuous increase in strain rate,more pronounced failure characteristics were observed.LSSG was divided into three parts by additional cracks,and the final failure was crushing along the axial pressure direction (Xue et al.,2021).

(4) For the samples with 7% Na2SiO3,when the strain rate was 57.953 s-1,the failure characteristics observed were minor,with cracks only appearing at the edge of the failure surface without extending further.When the strain rate increased to 97.651 s-1,the cracks appeared on the surface of large fragments.Notably,axial splitting failure was observed.

5.Energy dissipation in SHPB test

5.1.Principle and calculation of energy dissipation

The destruction of the LSSG samples is accompanied by energy dissipation.Moreover,energy conversion is irreversible and results in deformation.The study of energy conversion in LSSG under impact load is beneficial for elucidating the failure mechanism of the samples (Zheng et al.,2021).

According to the energy conversion principle and stress wave transfer rule,the incident energyQI,reflected energyQR,and transmitted energyQTcan be calculated as follows:

The absorbed energy of the sample when failure occurs is written as follows:

In general,the energy absorbed by LSSG is transformed into breaking energy.When the dissipative energy in the sample decreases,the cracks appear,the sample deforms less,and the incidence of failure decreases.

5.2.Energy law in SHPB test

Fig.15 shows the energy changes in LSSG containing 5%Na2SiO3under different strain rates.The incident and absorbed energy in LSSG increases continuously with time,but the increment differs.When the increase rate is slow,it stabilizes after a certain duration.Regarding the incident energy of the sample,however,the change trend is not prominent with the increase in time (Ma et al.,2018).Compared with the incident energy,the value of the absorbed energy was very small.At the strain rates of 57.435 s-1,82.516 s-1and 109.825 s-1,the magnitudes of the incident energy were approximately 9,22 and 16 times that of the absorbed energy.

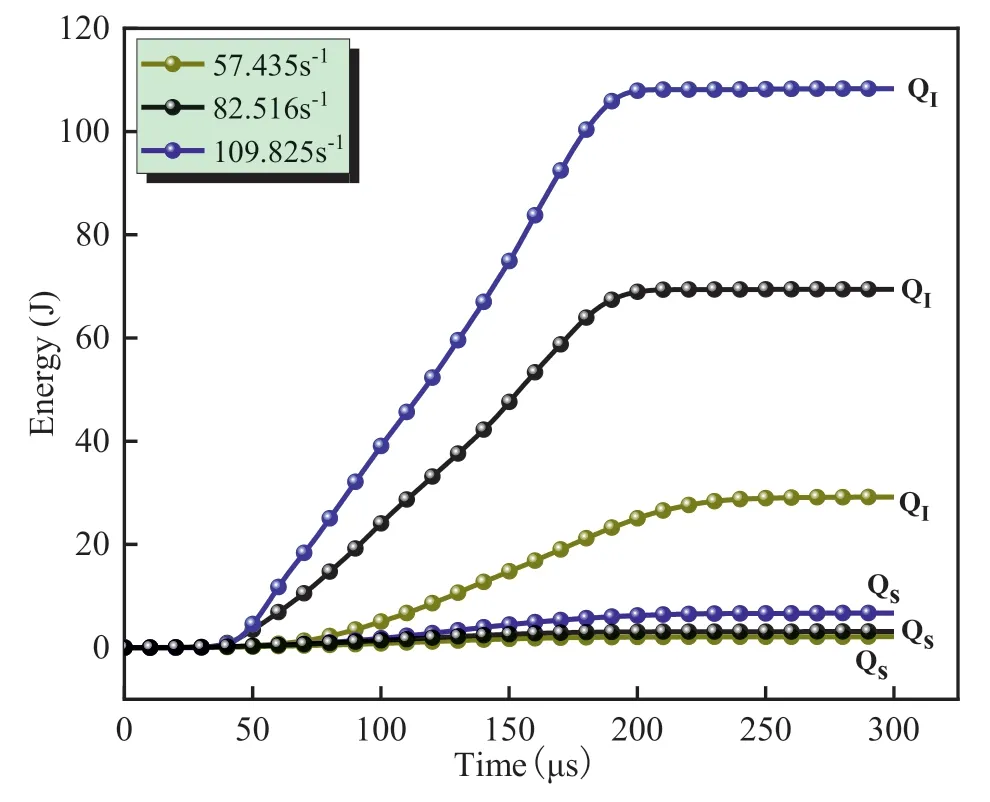
Fig.15.Energy variation curves of LSSG under different air pressures.

Fig.16 shows the influence curve of different Na2SiO3contents(1%,3%,5% and 7%) on the energy variation of LSSG.Noticeably,under the same pressure,LSSG with 5% Na2SiO3had the highest and lowest incident and absorbed energy,respectively.The absorbed energy in the sample with a Na2SiO3content of 1% was significantly higher than that of other samples.The peak values were 1.47,4.5 and 1.92 times the absorbed energy of the samples with Na2SiO3contents of 3%,5% and 7%,respectively.

Fig.16.Energy variation curves of LSSG with Na2SiO3 content.

The aforementioned observation is attributable to a lower Na2SiO3content,resulting in a worse bonding performance between the particles in the sample and the appearance of more cracks.Under axial air pressure,the energy absorbed by the LSSG was manifested in the expansion of external cracks,resulting in the samples entering an unstable state (Fu et al.,2017;Li et al.,2019).

It is important to determine the magnitude of energy absorbed by LSSG under different strain rates.Accordingly,the absorbed energy of LSSG was calculated.Fig.17 presents the relationship among absorbed energy,sodium silicate content and strain rate,which could be written as follows:

Fig.17.Fitting surface among absorbed energy,sodium silicate content and strain rate of LSSG.

whereQsrepresents the absorbed energy(J),ε represents the strain,andNrepresents the Na2SiO3content (%).

Fig.18 depicts the relationship of absorbed energy with air pressure.The absorbed energy (QS) and air pressure (P) have a strong linear relation.The fitting equations are listed in Table 4.

Fig.18.Relationships between absorbed energy and air pressure of LSSG.

Table 4 Fitting equations (QS= aP + b) for describing the relationships between absorbed energy and air pressure.

Fig.18 shows that the absorbed energy of LSSG increases as air pressure increases,and the absorbed energy increases by approximately 1.18,1.21,1.94 and 0.78 times,respectively,when the air pressure increases from 0.2 MPa to 0.4 MPa.This indicates that with the continuous increase in air pressure,the energy absorption ability of the sample is strengthened,as manifested by an increasing number of cracks in the sample.Among them,the absorbed energy of LSSG with 5%Na2SiO3increases,and the sample is less damaged than other samples.

The Samples containing 5%Na2SiO3were analyzed to determine the link between failure mode,absorbed energy per unit volume,and strain rate,and their relationships are shown in Fig.19.

Fig.19.Absorbed energy per unit volume and failure mode of LSSG.

As shown in Fig.19,the absorbed energy per unit volume in LSSG increases with the average strain rate,which indicates the presence of a certain correlation between the absorbed energy of the LSSGs and the average strain rate.When the average strain rate increases,the number of cracks in the sample continuously increases,which results in the increasing absorbed energy per unit volume.Meanwhile,the failure mode of the samples gradually changes from minor failure to partial crushing with increasing strain rate(Song et al.,2022b;Xu et al.,2022).

Therefore,the absorbed energy per unit volume of LSSG can better reflect the failure mode and dynamic strength,and studying the absorbed energy of LSSG is helpful to make full use of its dynamic characteristics.

6.Dynamic damage constitutive model of LSSG

The ZWT model is generally used to describe the mechanical properties of materials.Specifically,it is suitable for elucidating the mechanical properties of geopolymer materials when the strain rate ranges from 10-4s-1to 103s-1.The constitutive model(Fig.20) generally consists of a nonlinear elastic model,lowfrequency Maxwell element,and high-frequency Maxwell element (Can et al.,2015).

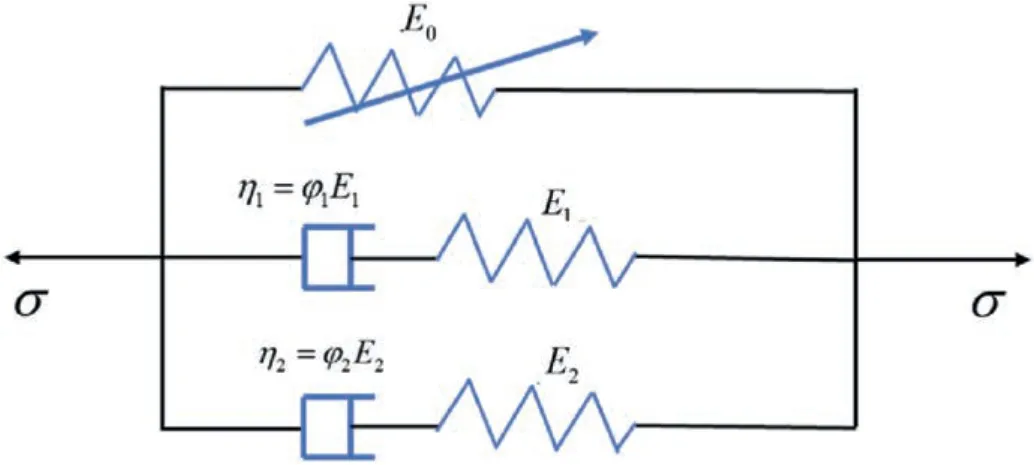
Fig.20.ZWT model.

The φ1and φ2ranges are 10-100 s and 10-4-10-6s,respectively.Generally,φ1mainly controls the low strain rate part,whereas φ2controls the high strain rate part (Dong et al.,2018).

The ZWT model is described as follows:

where σ is the dynamic stress;E0,α and β are the nonlinear elastic constants of the body;E1andE2are the elastic moduli of the Maxwell bodies;φ1and φ2are the low-frequency and highfrequency relaxation times,respectively;and δ is the time,whose value range is [0,t].

Because the time scale of the SHPB test is very short(usually 1-100 μS),the low-frequency Maxwell body does not have enough time to relax.Therefore,it can be regarded as a linear elastic body with an elastic modulus ofE1.Eq.(4) can be rewritten as

Because the first term in Eq.(5)is unrelated to the strain rate,it only represents the equilibrium mechanical effect of samples under impact loads.Moreover,LSSG exhibited the characteristics of small strain during the test,and αε2+βε3is almost negligible (Xie and Yan,2019).Thus,Eq.(5) can be rewritten as

Because the LSSG is a heterogeneous material with numerous internal cracks and holes,it undergoes deformation-induced damage when subjected to impact loads.Therefore,factors such as damage and deformation need to be considered in the constitutive model.The ZWT model is improved,and the continuous damage mechanics model is introduced to obtain the following equation:

where σ*is the effective stress.According to the literature (Wang et al.,2008;Zhou et al.,2022),all microelements in an LSSG obey the Weibull distribution,thus the damage factor of LSSG can be defined as follows:

where εlis the cumulative damage threshold strain of the LSSG,and εl=0.5εmax,in which εmaxis the strain corresponding to the peak stress;and ωandζ are the damage evolution parameters.

Therefore,the dynamic model of LSSG considering the damage can be obtained as follows (Ren et al.,2018),as shown in Fig.21:

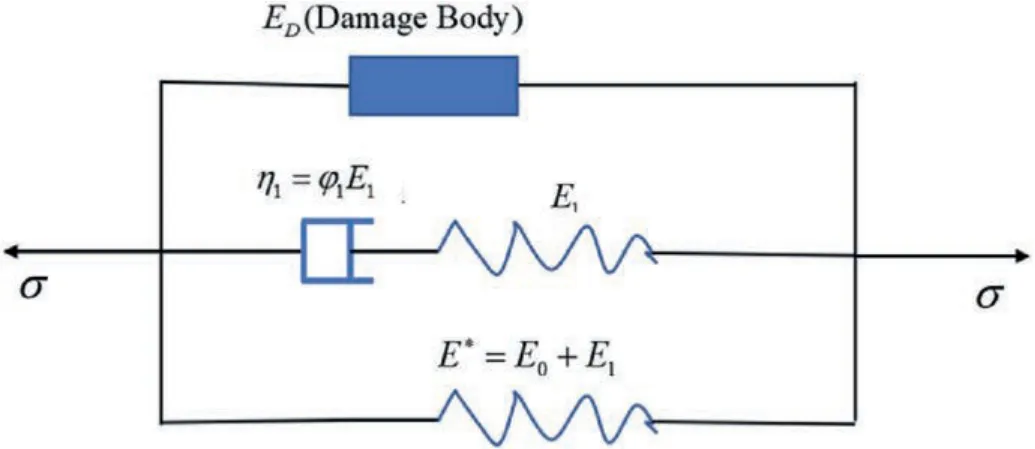
Fig.21.Constitutive model of LSSG considering damage.

The equation fitting diagrams of LSSG with Na2SiO3contents of 1%,3%,5% and 7% are drawn according to the constitutive model equation,and the correlation coefficients are all greater than 0.9,as shown in Fig.22.The fitting results demonstrate that the experimental and theoretical curves are largely consistent,indicating that the constitutive model of the LSSG constructed in this paper considering damage can better reflect its dynamic stress-strain characteristics.

Fig.22.Verification of the LSSG constitutive equation considering damage: (a) 1% Na2SiO3.(b) 3% Na2SiO3(c) 5% Na2SiO3(d) 7% Na2SiO3.

7.Conclusions

The dynamic properties of LSSG are studied through an SHPB uniaxial impact test.The characteristics of the dynamic stressstrain curve are analyzed,and the dynamic compressive strength varies with the Na2SiO3content,curing age and strain rate.

Moreover,the failure mode of LSSG is determined,and a damage constitutive model for LSSG is constructed.The following conclusions are drawn:

(1) The dynamic stress-strain curve of LSSG mainly comprises the following five states: the particle compaction,linear elastic,crack appearance,crack extension,and failure states.The peak stress increases with the increasing strain rate.Under a strain rate of 109.825 s-1,the peak stress can reach 20.03 MPa.

(2) The dynamic compressive strength of LSSG with a curing age of 28 d is significantly higher than that of LSSG with a curing age of 7 d.The dynamic compressive strength of LSSG first increases and then decreases with increasing Na2SiO3content,and the compressive strength is the largest when 5%Na2SiO3is added.

(3) The strain rates of all LSSGs ranges between 40 s-1and 110 s-1.With an increasing average strain rate,the dynamic compressive strength of LSSG exhibits an upward trend.The higher the Na2SiO3content,the greater the influence of the average strain rate on the dynamic compressive strength.

(4) The failure characteristics of LSSG under different strain rates differ under impact loading.The higher the strain rate,the more severe the specimen fracture.When the LSSG with 1%Na2SiO3is damaged,the sample is in a crushed state,with almost no large fragments.With the continuous increase in Na2SiO3,the damage degree of the sample decreases markedly.When the Na2SiO3content is 5%,no crushing is accompanied with damage to the sample.Only the number of cracks increases,and the ultimate failure is through crushing along the axial pressure direction.

(5) A change in energy during impact loading occurs in the impact test on the LSSG.Under the same pressure,the incident energy of LSSG with a Na2SiO3content of 5% is the largest,and the absorbed energy is the smallest;the absorbed energy of the sample with a Na2SiO3content of 1%is the highest.This indicates that the damage to the sample is the severest at this dosage.

(6) The ZWT equation is simplified based on the analysis of the ZWT model and the linear stress-strain curve obtained from the SHPB impact test.Moreover,the dynamic constitutive model of LSSG is established by comparing the stress-strain curves for different strain rates.The results demonstrate that the constitutive model is in a good agreement with the constitutive curve of LSSG obtained from the test.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.