A novel relationship between elastic modulus and void ratio associated with principal stress for coral calcareous sand

Ran Gao,Jianhong Ye,*

a State Key Laboratory of Geomechanics and Geotechnical Engineering,Institute of Rock and Soil Mechanics,Chinese Academy of Sciences, Wuhan,430071,China

b University of Chinese Academy of Sciences, Beijing,100049, China

Keywords: Coral calcareous sand (CCS) Elastic shear modulus Elastic bulk modulus Triaxial test Estimation formulation Ye formulation

ABSTRACT Elastic moduli,e.g.shear modulus G and bulk modulus K,are important parameters of geotechnical materials,which are not only the indices for the evaluation of the deformation ability of soils but also the important basic parameters for the development of the constitutive models of geotechnical materials.In this study,a series of triaxial loading-unloading-reloading shear tests and isotropic loading-unloadingreloading tests are conducted to study several typical mechanical properties of coral calcareous sand(CCS),and the void ratio evolution during loading,unloading and reloading.The test results show that the stress-strain curves during multiple unloading processes are almost parallel,and their slopes are much greater than the deformation modulus at the initial stage of loading.The relationship between the confining pressure and the volumetric strain can be defined approximately by a hyperbolic equation under the condition of monotonic loading of confining pressure.Under the condition of confining pressure unloading,the evolution of void ratio is linear in the e-lnp′ plane,and these lines are a series of almost parallel lines if there are multiple processes of unloading.Based on the experimental results,it is found that the modified Hardin formulae for the elastic modulus estimation have a significant deviation from the tested values for CCS.Based on the experimental results,it is proposed that the elastic modulus of soils should be determined by the intersection line of two spatial surfaces in the G/K-e-p’/pa space(pa:atmosphere pressure).“Ye formulation” is further proposed for the estimation of the elastic modulus of CCS.This new estimation formulation for soil elastic modulus would provide a new method to accurately describe the mechanical behavior of granular soils.

1.Introduction

Elastic shear modulusGand elastic bulk modulusKare well known because they are essential measures of soil deformation ability and the fundamental parameters for the development of soil constitutive models.Numerous studies have been conducted on how these two moduli can be estimated.For example,Hardin and Richart (1963) and Richard et al.(1970) clearly found that the elastic shear modulus of soil was affected by the mean effective stress,void ratio,and the over-consolidation ratio,and they further suggested the earliest estimation formula for the elastic shear modulus as

whereG0,ψ,α andkare the material-related dimensionless parameters;OCRis the over-consolidation ratio;eis the void ratio;andp′is the mean effective principal stress.Hardin and Richart(1963) suggested that ψ=2.17 if the void ratio is in the range of 0.3-0.8 for the sand with rounded granular,and ψ=2.97 if the void ratio is in the range of 0.6-1.3 for angular sand soil.It is easy to notice that the physical dimensions at both sides of Eq.(1) are inconsistent when the material parameter α≠1.This is an obvious defect.

Subsequently,Seed and Shannon (1970) developed another estimation formulation for the elastic shear modulus of soils under small strain condition:

whereKmaxis a dimensionless material parameter,andparepresents the atmospheric pressure.The dimension at both sides in Eq.(2)is matched because of the introduction of atmospheric pressure.However,the effect of the void ratio is not considered in Eq.(2).Later,Iwasaki and Tatsuoka (1977)proposed a similar formula:

In Eq.(3),the introduction of Skempton’s pore pressure coefficientBmeans that soil saturation was taken into consideration.The material parametersAandnare correlated with shear strain γ.Similar to Eq.(1),the physical dimension at both sides of Eq.(3)is not matched whenn(γ)≠1.Furthermore,the specific expressions ofA(γ)andn(γ)are difficult to be explicitly determined,resulting in that Eq.(3)being difficult to be used.Some scholars have also found that the factors,such as the coefficient of uniformityCu(Menq et al.,2003),fine particles contentFc(Wang and Kuwano,1999),mean particle diameterD50(Hardin and Kalinski,2005),and particle shape all have some effect on the elastic shear modulus of soil.However,the key influencing factors are still the void ratioe,as well as the mean effective principal stressp’.Since then,based on the work of Hardin and Richart(1963)and Richard et al.(1970),several scholars have made some minor corrections and improvements to these Hardin formulae.Several formulae for the estimation of elastic shear modulus which could only be applicable to some particular materials or under some special conditions (Wang and Zhang,2007;Sun and Huang,2011;Hu et al.,2011;Gao et al.,2013;Liu et al.,2017;Ovalle and Hicher,2020) were further proposed,the most popular form is

whereG0is a material parameter with the physical unit Pa,and α is a coefficient related to material property.Eq.(4)was referred to as the modified Hardin formula in the literature.

Hardin’s formula actually is only an estimation formulation for the elastic shear modulus under the condition of small strain(generally less than 1%) involved in the resonance column test.Strictly speaking,the estimated results of the above Hardin’s formula cannot be utilized in numerical modeling when a large deformation occurs.However,the elastic modulus of granular materials under large strain condition(>1%,even up to 35%which is impossible to be reached in the resonance column test) is an important parameter when forming the elastic stiffness matrix[De]in numerical modeling under the classical framework of elastoplastic theory,which will directly affect the reliability of computational results.However,there is still a lack of a reliable formula for the estimation of the elastic modulus under the condition of large strain.If Hardin’s formula is used for the estimation of elastic modulus at large strain,it would inevitably lead to a large discrepancy with test results.Therefore,it is necessary to propose some new estimation formulations for the elastic modulus of soils under the condition of large strain.Moreover,these estimation formulae mentioned above are primarily applicable to terrestrial soils,e.g.quartz sand and river sand.It needs to be further explored whether they could be applied to the CCS widely existing in the marine environment.

Coral calcareous sand (CCS),also known as carbonate sand or coral sand(Coop,1990),is composed of marine bioclastic sediments and is widely distributed in the South China Sea (SCS),Southeast Asia,the Middle East,the South Pacific Islands,and other areas,and it is a special geotechnical material with substantial differences from terrestrial soils.CCS has the characteristics of extreme angularity of particles shape,easily crashing,rough particles surface,and great friction angle.Its main mineral composition is calcium carbonate.CCS is the main material for the foundation of structures constructed on the reclaimed lands in the SCS.In recent decades,CCS receives considerable attention largely prompted by the exploitation of oil/gas in the offshore environment,such as the Australian North-West shelf,and by the civil infrastructure construction,e.g.the palm islands at Dubai in the United Arab Emirates,and these reclaimed lands on the top of natural coral reefs in the SCS.Many research works have been carried out on the mechanical properties of CCS,such as the quasi-static mechanical property (Coop,1990;Coop and Atkinson,1993;Porcino et al.,2008;He et al.,2021,2022;Wang et al.,2022),dynamic property and liquefaction (Hyodo et al.,1998;Coop and Qadimi,2007;Lopez-Querol and Coop,2012;Xiao et al.,2018;Gao and Ye,2019;Lv et al.,2019;Ding et al.,2021),bearing capacity (Wang et al.,2009,Wang et al.,2021b;Wan et al.,2021),creep behavior(Wang and Cai,2017;Wang et al.,2018;Cao and Ye,2019;Ye et al.,2019) and particles breakage (Coop et al.,2004;Donohue et al.,2009;Miao and Airey,2013;Yu,2018;Suescun-Florez et al.,2020;Cheng and Wang,2021;Kuang et al.,2021;Lv et al.,2021;Wang et al.,2021a;Chen et al.,2022;Zhou et al.,2022).There are also some studies on the shear modulus of coral sand under small strain condition,such as Shi et al.(2021,2022) and Giang et al.(2017).Furthermore,what they focused on in these previous works is generally the deformation modulus,rather than the elastic modulus.To the best knowledge,there are few studies on the elastic shear and bulk modulus of CCS,and their relationship with the void ratio and applied effective stress under large strain condition so far.At present,Eq.(4)is still occasionally used to estimate the elastic modulus of CCS under large strain condition.Unfortunately,the suitability of Eq.(4) has still not been verified for CCS under large strain condition.A series of triaxial loading-unloadingreloading shear tests and isotropic loading-unloading-reloading tests are performed in this study for the problem of the estimation of the elastic modulus of CCS.The CCS sampled from the SCS is used to prepare the test specimens.The elastic modulus can be measured from the stress-strain curves recorded during the elastic stage in the unloading-reloading process.By comparing the estimated values of the modified Hardin Formulae (Eq.(4) and (12))with the measured results,the suitability of the modified Hardin Formulae for CCS could be checked.

Meanwhile,based on the experimental results,two new formulae are proposed in this study for the estimation of the elastic shear and bulk moduli of CCS.As a consequence,a new group of relationships between the elastic modulus,void ratioe,and the mean effective principal stressp′is successfully established.The comparative study shows that the new formulae established in this study have better estimation accuracy and more explicit physical meaning than the modified Hardin formula.It will offer a new idea for the development of constitutive models to describe the mechanical behavior of soils,especially for the CCS.

2.Materials and test plan

2.1.Material

The samples of CCS used in the test were all sampled from a reclaimed land in the SCS.At the engineering in-site,we performed more than 100 times of particle gradation tests and found that the grain size distribution (GSD) of the CCS varied significantly from place to place on the reclaimed land.The average GSD of these test results at the in-site is selected as the representative in this experiment program,as shown in Fig.1.The coefficient of uniformityCu=6.18 and the coefficient of curvatureCc=1.35.The basic physical parameters of the CCS used in the test are listed in Table 1.

Fig.1.The average GSD curve of the CCS used in this study: (a) Full particle size and (b) Used particle size less than 5 mm.

Table 1 Basic physical parameters of CCS used in the test.

Table 2 Test conditions for the isotropic loading-unloading-reloading tests of confining pressure.

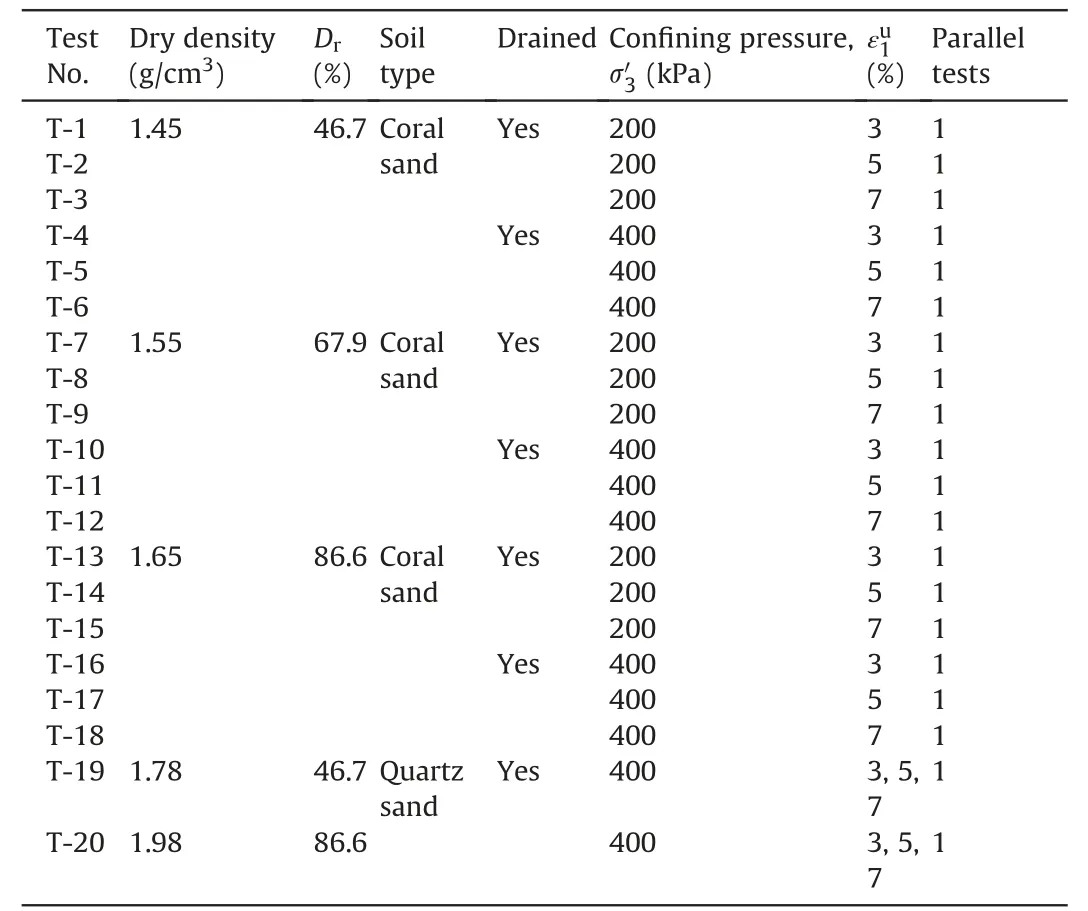
Table 3 Test conditions for the triaxial loading-unloading-reloading shear tests.

2.2.Specimen preparation

Eight hours of high-temperature dehydration and the subsequent natural cooling have to be done,to ensure the sand particles are completely dry.Then the coral sand samples are sieved and proportioned according to the GSD illustrated in Fig.1b.The sand sample of each specimen was equally divided into seven parts and then poured into a cylindrical rubber membrane to make a cylindrical specimen with a diameter of 70 mm,and with a height of 140 mm.A suction cap in which a negative pressure has been generated is connected to the mold,making the rubber membrane tightly against the inner wall of the mold.The predetermined height (20 mm) of each layer is reached by the way of knocking.Since the compression process was done without a compaction hammer,only a very small amount of particle breakage would exist during the preparation.After the specimen has been made,the specimen average volume can be calculated by measuring the diameter of the top,middle and bottom of the specimen with vernier calipers,then the dry density of the specimen can also be obtained.If there is a large error with the target dry density,this specimen should be re-prepared.

2.3.Test plan and test instrument

All the tests are designed as the saturated drainage test,to reliably measure the volumetric strain of each specimen.Two parallel tests under the same condition are carried out to ensure the reliability of the test data.The dry densities of specimens are set as 1.45 g/cm3,1.55 g/cm3,and 1.65 g/cm3,respectively.The test plans are shown in Tables 2 and 3.It is known that 6 groups of isotropic loading-unloading-reloading tests,and 18 groups of triaxial loading-unloading-reloading shear tests will be conducted.All the tests are performed on the GDS DYNTTS equipment made in the UK.The measuring range of the load cell is 10 kN with an accuracy of 0.0001 kN.The measuring range of the piston-type volumetric controller is 250 mL with an accuracy of 0.001 mL.The DYNTTS equipment employed in the tests is shown in Fig.2.

Fig.2.The equipment DYNTTS employed in the test.

For the purpose of comparison and verification,four quartz sand specimens with two different dry densities,and with the same GSD of the CCS illustrated in Fig.1b are prepared through artificial mixing.Among them,two specimens are for the isotropic loading-unloading-reloading test,and another two for the triaxial loadingunloading-reloading shear test.To ensure the comparability of the test results between CCS and quartz sand,the relative densities of the quartz sand specimens are set as same as the counterparts of CCS.Correspondingly,the dry density of quartz sand specimens is set as 1.78 g/cm3(medium dense state,Dr=46.7%)and 1.98 g/cm3(dense state,Dr=86.6%),respectively.The basic properties of the quartz sand are listed in Table 1,and the test conditions for the quartz and specimens are listed in Tables 2 and 3

3.Experimental results and discussion

3.1.Elastic shear modulus

Typical stress-strain curves of the CCS and quartz sand withDr=46.7% recorded in the triaxial loading-unloading-reloading shear test are illustrated in Fig.3.It is observed that the development trend of the stress-strain relationship during the unloading and reloading of deviatoric stress cannot radically be changed,and finally,the critical state can be eventually reached.The stress-strain curves during several unloading stages are almost parallel with a great slope,and their slope slightly reduces at the end of each unloading stage.In Fig.3a,it is also observed that each unloading curve and the corresponding reloading curve almost coincide,until the time when the plastic strain starts to be produced.After plastic strain is produced,the stress-strain curves at the unloading and reloading stage gradually separate.When the plastic strain is initially produced,the stress-strain relation gets into the elastoplastic stage (marked as EP-S in Fig.3a) from the elastic stage(marked asE-S in Fig.3a).The corresponding point on the stressstrain curves is called the elasto-plastic separation point in this study,as marked by a series of short horizontal red lines in Fig.3a.During the entire unloading-reloading process,it is found that the hysteresis loops are small or even absent.This characteristic is basically the same as that of quartz sand,but the area of these hysteresis loops of CCS is generally less than that of the counterparts of quartz sand.

Fig.3.Typical stress-strain relationship of CCS and quartz sand under the condition of deviatoric stress loading-unloading.

This phenomenon implies that elastic deformation is mainly produced during the unloading and reloading processes,only a small amount of plastic deformation has been produced at this stage.Based on this recognition,Young’s modulusEand Poisson’s ratio ν can be determined in this study from the stress-strain relation recorded during the elastic unloading stage.The elastic shear modulusGand ν then can be calculated using the following formulae:

where εris the radial strain,and εais the axial strain of specimens.

By substituting the void ratioeand the mean effective principal stressp′recorded during tests into the modified Hardin formula(Eq.(4)),the elastic shear modulusGof the CCS can be estimated.The comparison between the estimated value and the tested value is demonstrated in Fig.4a,c and e.It is found that the value range of the estimated elastic shear modulusGadopting the modified Hardin formula (Eq.(4) is relatively narrow and the maximum estimated value is much less than the maximum measured value,while the minimum estimated value is greater than the minimum measured value.It is well illustrated by Fig.4a,c and e that there is a significant discrepancy between the estimated values (marked as triangles) adopting the modified Hardin formula (Eq.(4)) and the measured values(marked as circles).Therefore,Eq.(4)is invalid for the estimation of the elastic shear modulus of CCS under the condition of large strain.Based on this recognition,it is not recommended to adopt the modified Hardin formula(Eq.(4))in the development of the constitutive models for CCS.

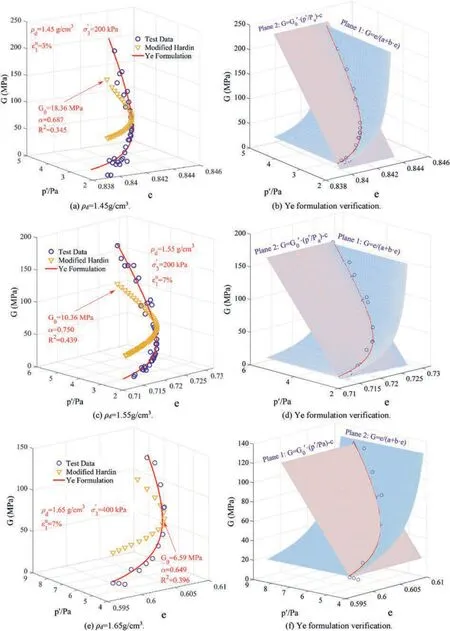
Fig.4.Comparison and validation of the typical tested values of the elastic shear modulus of CCS with different estimation formulae.

Since previous estimation formulae are not applicable to CCS,a new set of estimation formulae based on the experimental results will be proposed in this study.A large number of previous studies have shown that the void ratioeand mean effective principal stressp′are decisive influencing factors for the modulus estimation.Through comprehensive analysis of these test data,it is found that there is indeed a more explicit relationship among the elastic shear modulusG,void ratioeandp′.The relationship between them can be described by the following formula:

wherepa=100 kPa is the atmospheric pressure;anda,b,candare the fitting parameters,depending on the dry density,applied confining pressure,as well as axial strain at unloading.In this study,this estimation formula is named ‘Ye formulation’ for the elastic shear modulus.It is shown by Eq.(7)that the relationship between the elastic shear modulusGand void ratioeis hyperbolic,and thereis a linear relationship between the elastic shear modulusGand the mean effective principal stressp′.The fitted values ofa,b,candfor the experimental data adopting Eq.(7) are listed in Table 4.

Table 4 Fitted values of a, b,c and in the ‘Ye formulation’ for the G of CCS.

Table 4 Fitted values of a, b,c and in the ‘Ye formulation’ for the G of CCS.

It can be seen in Table 4 that it is credible to describe the physical relationship betweenG,eandp′/paby the hyperbolic and linear relationships formulated in Eq.(7),and the correlation coefficientR2is generally greater than 0.9 with a minimum of 0.82.While,the correlation coefficientR2from modified Hardin formula are mostly around 0.4.Therefore,it is implied that the elastic shear modulus of sandy soils can be estimated by adopting Eq.(7)inG-e-p′/paspace with a better ability.In Table 4,one can see that the values of the parametersa,b,candG′0exhibit a large dispersion.It is quite difficult for us to find some unified formulae to describe the relationship between thea,b,c,and the dry density,applied confining pressure,as well as the axial strain at unloading.This dispersion for the values ofa,b,candshould be attributed to the inevitable test errors,as well as the high sensitivity of thea,b,candto the test data.Further research is needed in the future.

Further analysis on Eq.(7)confirms that the two equations in Eq.(7)describe a curved surface and a plane,respectively inG-e-p′/paspace,as shown in Fig.4b,d and f.The relationship among the elastic shear modulus of sandy soilsG,eandp′/painG-e-p′/paspace is a spatial curve,and this spatial curve must be the intersection line between the curved surface and the plane described by the two equations in Eq.(7),as illustrated in Fig.4b,d and f.The results shown in Fig.4 have clearly demonstrated that the estimated results of the elastic shear modulus by Eq.(7) proposed in this study for CCS based on the concept of two surfaces intersection are more accurate and credible,compared with the modified Hardin formula (Eq.(4)).

3.2.Elastic bulk modulus

The typical stress-strain curves of CCS recorded in the isotropic loading-unloading-reloading test are shown in Fig.5.It is observed in Fig.5 that the unloading and reloading process of confining pressure cannot fundamentally change the development pattern of the confining pressureversus the volumetric strain εv.It means that the curves passing those initial unloading points in the-εvcoordinates basically are the same as that under monotonic loading.If the volumetric strain at unloadingin the horizontal axis is normalized adopting the current void ratioeto eliminate the effect of dry density on the stress-strain relation,then the full process relationship of the confining pressureversus the volumetric strain/ecan be approximately described by the hyperbolic equation under the conditions of isotropic consolidation compression,as demonstrated in Fig.6.In this study,once a reloading curve and its previous corresponding unloading curve are initially separated due to the generation of plastic strain,the confining stress at this moment is expressed as σu.Meanwhile,the confining pressure at the beginning time of unloading is expressed asIt is found in Fig.7 that the σuat the elastoplastic separation point is nearly half of the correspondingThat is to say,when the confining pressure at the reloading stage exceeds half of the correspondingin each unloading-reloading cycle,plastic deformation is produced again.As a result,the deformation of specimens gets into an elastoplastic stage from the elastic stage.The relationship betweenand εvat the unloading stage and subsequent reloading stage almost coincide before the appliedis less than the corresponding/2.In the overlapping part,certainly there is only elastic deformation has been produced.There is an obvious phenomenon in Fig.5 that the slope of the-εvcurves dramatically and gradually decreases when the appliedis less than 200 kPa,regardless of at the unloading or reloading stage.Correspondingly,the elastic bulk modulus reduces rapidly.It is indicated that the elastic bulk modulus is highly dependent on the applied confining stress for soils.

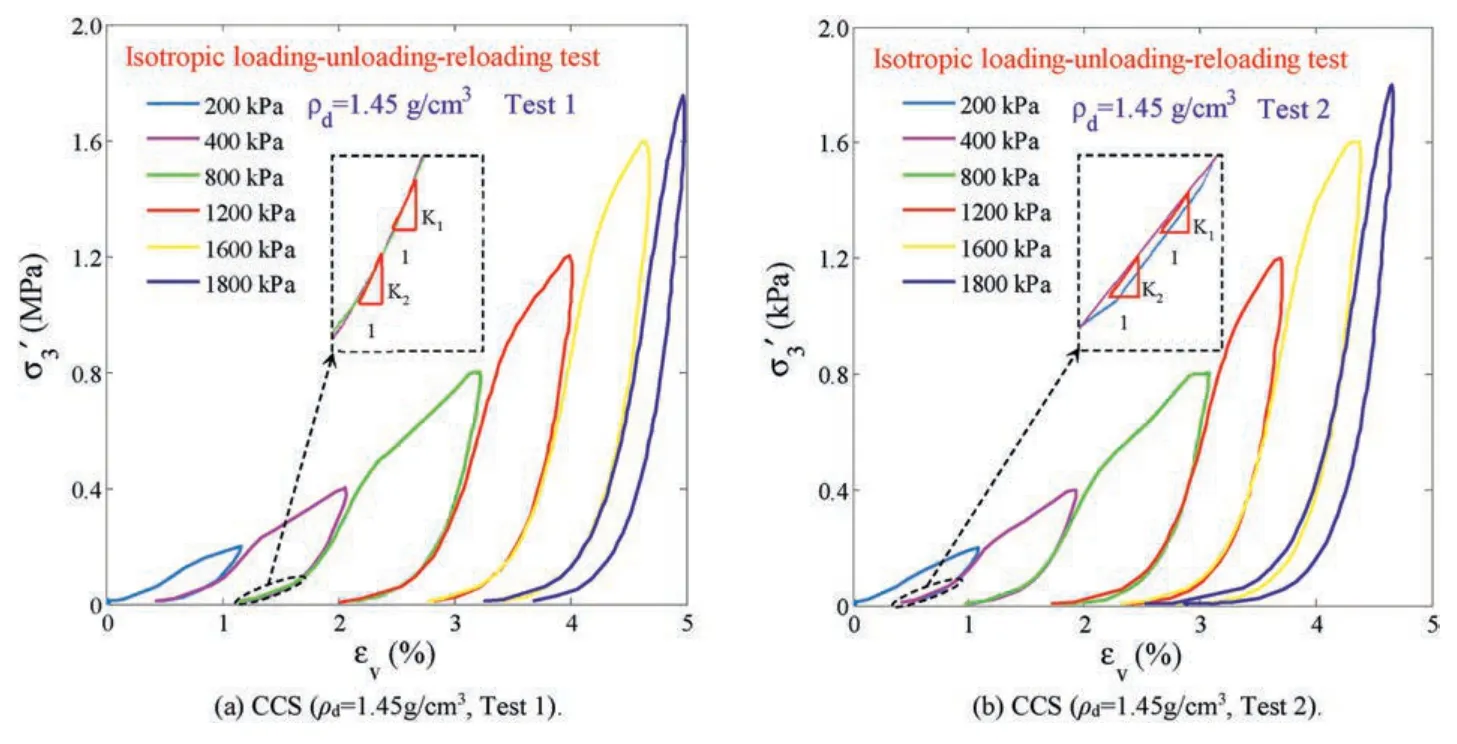
Fig.5.Typical stress-strain relationship of CCS recorded during the isotropic loading-unloading-reloading tests.Note: the elastic bulk modulus K is measured as the slope of the unloading and reloading -εv curves when they are basically overlapped.

Fig.6.Experimental relationship between the confining pressure at unloading and the corresponding normalized volumetric strain /e.Note: M and N are the fitting parameters.

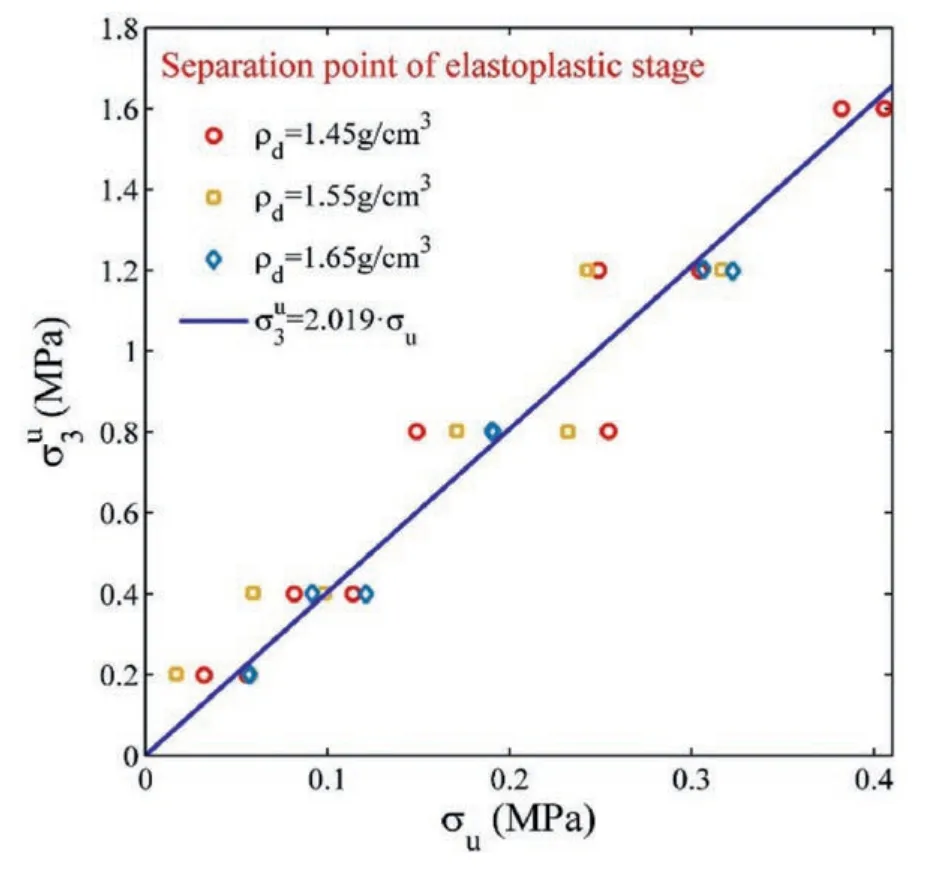
Fig.7.Experimental relationship between the stress σu at the elastoplastic separation point and the corresponding confining pressure at unloading

It is observed from the typical stress-strain curves measured in the isotropic loading-unloading-reloading tests,shown in Fig.5,that the greater the unloading confining pressurethe greater the bulk modulus at the initial unloading point,and the bulk modulus gradually reduces and eventually tends to 0 as the applied effective confining pressure decreases during unloading stages.It is indicated by this phenomenon that,like the elastic shear modulus,the elastic bulk modulus of soil represents a relationship with the mean effective principal stressp′,which can be described by

wherepa=100 kPa is the atmospheric pressure;K0is the elastic bulk modulus of soil whenp′=pa,which means thatK0is a constant parameter without a relationship withp′;andmis a dimensionless fitting parameter.It is obvious that the dimension at both sides of Eq.(8)is matched perfectly due to the introduction of the atmospheric pressurepa.

Here,a series of the elastic bulk moduli can be measured at the elastic deformation stage of each unloading-reloading cycle for each specimen,then theK0value of each specimen can be mathematically fitted adopting Eq.(8),as shown in Fig.8.It is observed that there is a nearly perfect linear relationship betweenKandp′/pawhen the applied confining pressure is less than 800 kPa.It means that the dimensionless fitting parameterm=1 is suitable for CCS.However,it is further surprised to find that the elastic bulk moduli of calcareous sand do not increase significantly when one specimen is unloaded from a high confining pressure (e.g.1600 kPa),relative to that when the same specimen is unloaded from low confining pressure (e.g.800 kPa).It was commonly believed that a specimen must be denser if it was isotopically compressed by higher confining pressure because the void ratio must reduce during the loading process,and a specimen with a less void ratio should have a greater elastic bulk modulus.Surprisingly,it is showcased in Fig.8 that the elastic bulk moduli of calcareous sand measured at the elastic deformation stage during these reloading processes are basically on the same line for the same specimen.It seems that the elastic bulk moduli of calcareous sand are only linear with the applied confining pressure,regardless of whether the specimens are unloaded from a high or low confining pressure.It is indicated by this phenomenon that the main influencing factor for the elastic bulk modulus of calcareous sand is the applied mean effective stress and the individual effect of the void ratio is insignificant.The reason is that the relationship between the lnp′and void ratioeat the elastic deformation stage during the isotropic reloading process is linear in the lnp′-ecoordinates (this characteristic will be presented thereafter).As a result,it is known that the void ratioeactually is the passive factor,and the applied mean effective stress is exactly the driving factor.Overall,the void ratioeis not an independent affecting factor for the elastic bulk modulus of calcareous sand.

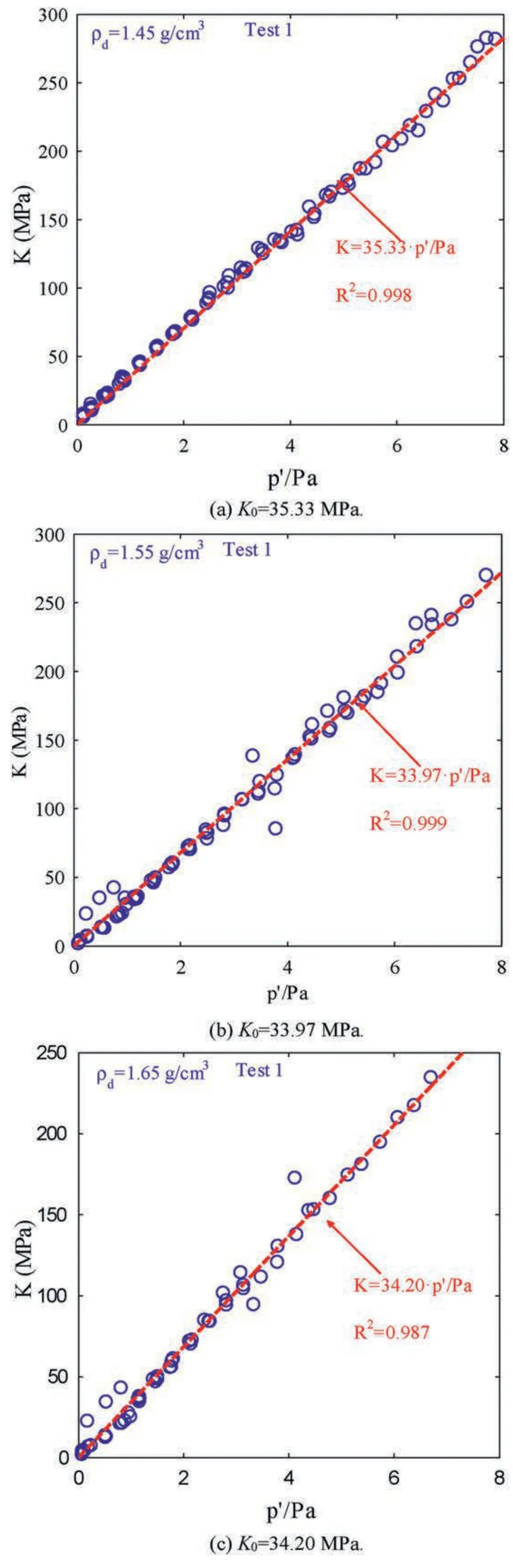
Fig.8.Experimental relationship between the elastic bulk modulus and the mean effective principal stress for CCS.

All experimental data recorded in the isotropic loadingunloading-reloading tests are mathematically fitted adopting Eq.(8),and the fitted values ofK0andmunder each test condition are listed in Table 5.As can be seen in Table 5,the experimental data recorded in the isotropic loading-unloading-reloading tests can be described remarkably by Eq.(8),with the majority ofR2greater than 0.99.It means that the reliability of Eq.(8) proposed in this study is good.Besides,it is found in Table 5 that the difference in the values ofK0is insignificant under the condition of different initial dry densities,and there is no obvious relationship between the elastic bulk moduli and the dry density.It is indicated thatK0is not sensitive to the initial dry density of the specimen,but should be closely related to the internal fabric of the specimen which is randomly formed in the process of specimen preparation.Due to the fact that the prepared specimens are impossible to be the same as each other from the perspective of the internal fabric,it is quite normal that the values ofK0determined from parallel tests are slightly different.

3.3.Normal consolidation line

Generally,a normal consolidation line(NCL)is considered as an approximate bi-linear relationship in the lnp′-eplane in the consolidation compression test for sandy soils in the field of critical state soil mechanics,taking the so-called pre-consolidation pressure as the transition point.The relationship between the void ratioeand the confining pressurep′of a NCL after the pre-consolidation pressure can be traditionally formulated by

where λ is the slope of the NCL,called as compression index;andeΓ is the void ratio of soils whenp′=1 kPa.

It is commonly known that particle breakage cannot occur under medium and low confining pressures for silica sands because they have very high particle strength,and the compression index λ generally is constant.CCS,however,has the characteristics of particle angularity and lower particle strength.Fig.9a,c and e shows the typical NCLs under isotropic consolidation condition for the CCS.It is found that these NCLs are not straight lines with a constant slope after the so-called pre-consolidation pressure,but are curves with a gradually increased slope.The increase of the slopes of NCLs is primarily due to the continuous particle crushing during isotropic consolidation.Before the initiation of particle crushing,the slopes of NCLs should be nearly constant.This phenomenon revealed here is the same as that observed by Coop,1993 and Altuhafi and Coop(2011).The compression index of the CCS can be determined according to the increment of its void ratio and the confining pressure following λp=-Δe/Δlnp′.The development of λpversus lnp′is illustrated in Fig.9b,d and f.It can be seen that the NCLs of CCS are indeed not straight lines with constant slopes.The λpof NCL is positively related to the applied confining pressure.It is found that quadratic polynomials can describe these curved NCLs when involving particles crushing:

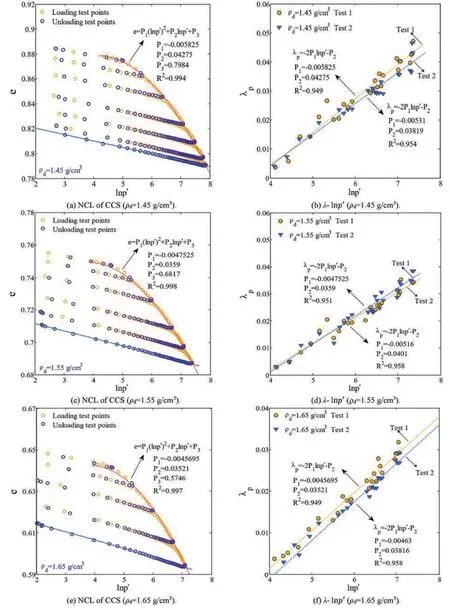
Fig.9.Typical test relationship between the void ratio e,compression index λ and lnp′ measured in the isotropic loading-unloading tests for CCS.

whereP1,P2andP3are three material-related parameters.

Due to the fact that the compression index is dependent onp′,rather than a constant,the NCL could be rewritten as

where λpis the compression index where the confining pressure isp′.Comparing Eq.(11) with Eq.(10),it is known that λp=-P1lnp′+P2,andeΓ=P3which is dependent on the initial dry density.As a consequence,Eq.(11) is formally consistent with the traditional expression of the NCL of sandy soils in which the compression index is constant.The compression index λp,however,is no longer constant but is related to the applied confining pressure,as illustrated in Fig.9b,d and f.Obviously,the effect of the particle breakage of CCS on the NCL has been taken into consideration appropriately through the varied λp.It should be noted that the increase of λpshould not be infinite.The increase of λpshould stop at ultra-high confining pressure,as the particle breakage of CCS must cease when the granular material reaches its ultimate particle size gradation (Altuhafi and Coop,2011),and the material will deform without further particle crushing.

Compared with that at the loading stage,the variation of void ratio is relatively simple during the unloading of confining pressure.It can be seen in Fig.9a,c and e that these unloading lines ine-ln(p′/pa)plane appear as a set of approximately parallel linear clusters approximately with the same slope,which can be described by the following formula in thee-ln (p′/pa) plane:

where λuis the slope of the unloading lines,andeuis the void ratio when confining pressure is unloaded top′=paon the unloading line.As analyzed above,these unloading lines are approximately parallel,therefore,λushould be constant,rather than depend on confining pressure.Eq.(12) is used to mathematically fit the experimental data,and the fitted values ofeuand λuunder different test conditions are listed in Table 6.It is shown that the descriptive ability of Eq.(12) is excellent becauseR2is all greater than 0.96.It can also be seen in Fig.9a,c and e that the reloading lines are basically overlapped with the corresponding unloading lines inelnp′plane.It is indicated that there is no significant plastic deformation produced in these specimens during the unloading and the subsequent reloading process of confining pressure for the CCS.

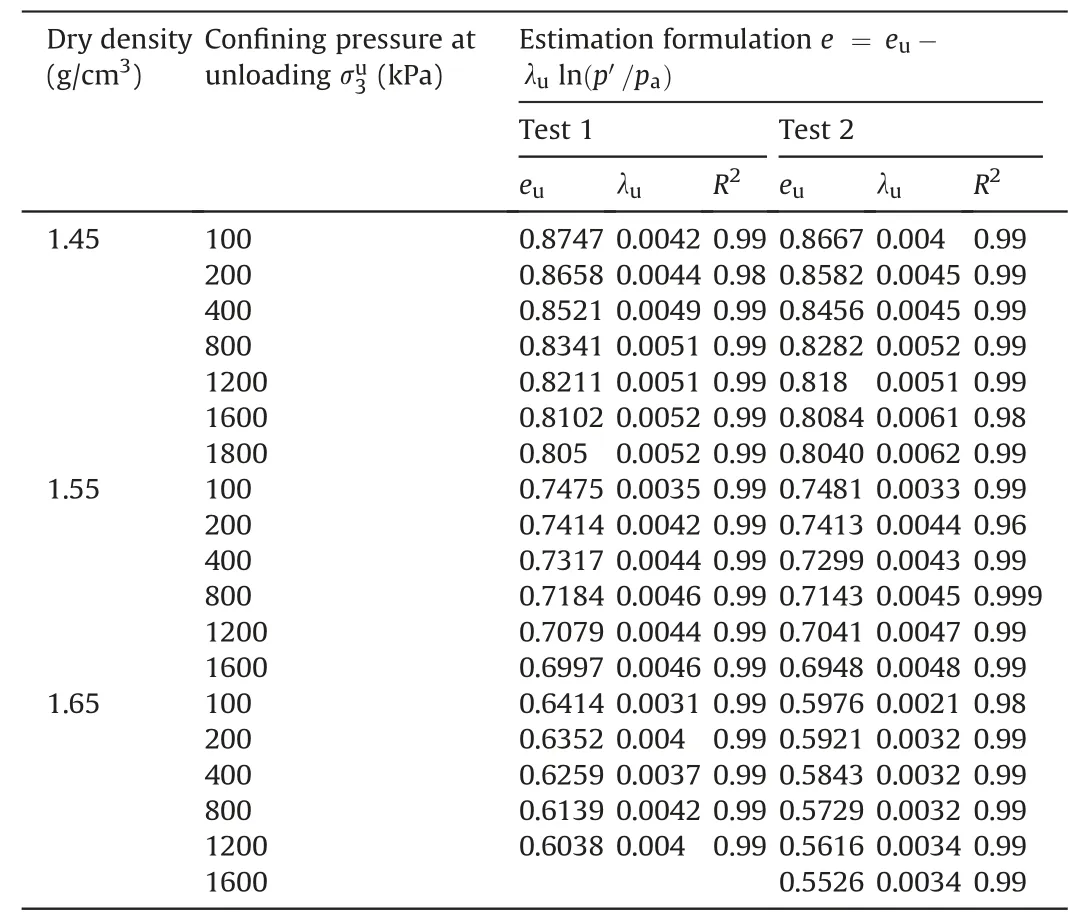
Table 6 Fitted values of eu and λu for the unloading lines under different test conditions(CCS).

The linear relationship between the elastic bulk moduleKand the mean effective principal stressp′/pahas been described by Eq.(8).Eq.(12) also has plausibly described the linear relationship between void ratioeand ln（p′/pa）during the elastic unloading stage.Then,the intersection lines of the two surfaces described by Eqs.(8) and (12) must represent the position of the elastic bulk modulusKin the three-dimensional spaceK-e-p′/pa,as shown in Fig.10b,d and f.Eqs.(8) and (12) are also referred to as ‘Ye formulation’ to form a group of formulae for the estimation of soil elastic modulus in this study.The modified Hardin formula for estimating the elastic bulk modulus of soil,similar to Eq.(4),is expressed as (Hu et al.,2018):

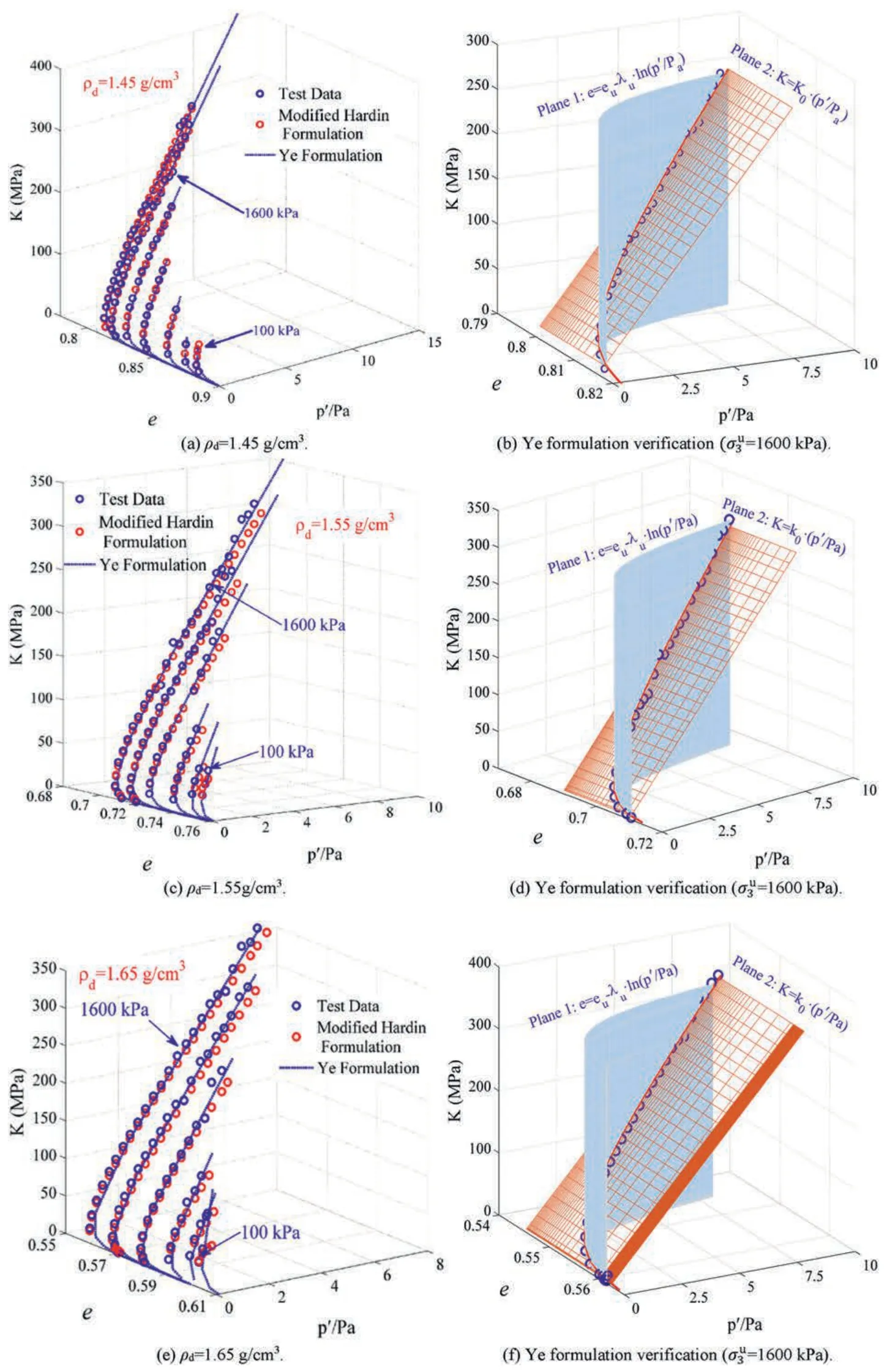
Fig.10.Comparison and validation of the modified Hardin formula and ‘Ye formulation’ with typical experimental results.

whereKhis a material parameter with the unit of MPa.

The modified Hardin formula (Eq.(13)) is also used to mathematically fit the experimental data,the fitted values ofKhand β are listed in Table 7,and the comparison with measured values are shown in Fig.10a,c and e.The comparison with the test data reveals that the estimated elastic bulk moduli adopting Eq.(13) is very closer to the experimental values.The fitted correction coefficientR2is generally greater than 0.9,but there is also aR2only equal to 0.59.Overall,the fitting result of the modified Hardin formula(Eq.(13)) is good.Nevertheless,this study would still not recommend the modified Hardin formula to be used for the elastic bulk modulus estimation,because the fitted values ofKhand β are different from case to case under different dry densities or differentFurthermore,it is quite difficult to establish an explicit relationship betweenKh,β and the dry densities,as well asbased on the data listed in Table 7.As a result,it will be very difficult to select the values ofKhand β under an arbitrary confining stress in numerical modeling.Taking the average for the values ofKhand β under differentvalues for one dry density may be a feasible way.However,the discrepancy between the estimatedKand measured values may also be difficult to be controlled.If Eq.(8) proposed in this study is used in numerical modeling,theKwill be easily and reliably estimated,because the power indexmis constantly equal to 1,and the coefficientK0is only related to the dry densities,as demonstrated in Table 5.

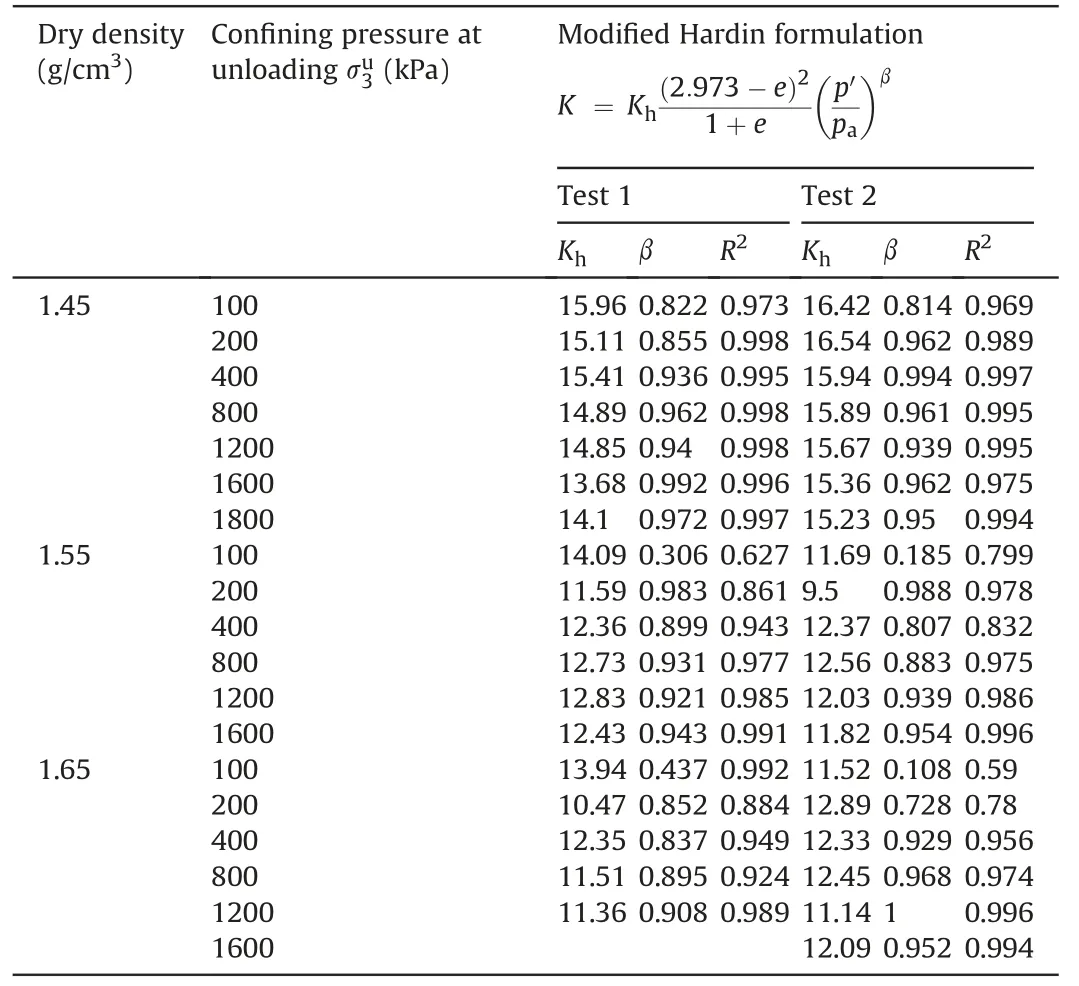
Table 7 Fitted values of Kh and β in the modified Hardin formula(Eq.(13))for the K of CCS.

It should be noted that the variableseandp′are independent of each other in the modified Hardin formulae(Eqs.(4)and(13)).Each of the two formulae describes only one curved surface in theG/K-ep′/paspace.If the relationship betweeneandp′is not constrained by equations,e.g.Eq.(12),it can be assumed that the value of the elastic modulus of soil could be an arbitrary position on the surface.This obviously is not agreeable with the actual situation observed in the tests that the elastic modulus varies along some curved lines in theG/K-e-p′/paspace (the experimental results have clearly revealed this feature).

The results shown in Figs.4 and 10 have fully demonstrated the feasibility and accuracy of ‘Ye formulation’ for the estimation of elastic modulus.Compared with the modified Hardin formula,‘Ye formulation’ has better credibility and suitability to a certain degree.

The fitted values of the parameterseuand λulisted in Table 6 are only applicable to the corresponding initial dry density and the unloading confining pressureTo overcome this limitation,the fitted values ofeuand λuin Table 6 are normalized to explore the relationship between the parameterseu,λuand the initial dry density and the unloading confining pressureIn this way,the application range of ‘Ye formulation’ (Eq.(12)) can be extended to any initial dry density and unloading confining pressure condition.By defining the state parameter Δe=e0-eu(e0is the initial void ratio),it is found that Δe/and λu/both have an exponential function relationship with the unloading confining pressureas shown in Fig.11.This exponential function can be described by

Fig.11.Experimental relationship between eu,λu and the initial void ratio e0,

3.4.Applicability to quartz sand

In the existing studies (Alikarami et al.,2015;Jafarian et al.,2018;Vranna et al.,2020),some experiments frequently are comparatively conducted on quartz sand to identify some unique behavior of CCS.In this section,to explore the applicability of the proposed‘Ye formulation’for the estimation of the elastic modulus of quartz sand,four quartz sand specimens with two different dry densities are prepared through artificial mixing,as mentioned in Section 2.Among them,Test Nos.I-4 and I-5 are for the isotropic loading-unloading-reloading test;meanwhile,Test Nos.T-19 and T-20 are for the triaxial loading-unloading-reloading shear test.

The experimental stress-strain relationships of quartz sand withDr=46.7% recorded in tests are illustrated in Fig.12.Compared with that in Fig.3,it is found that there is no essential difference in the triaxial loading-unloading-reloading curves between quartz sand and CCS.The only differences are that the peak shear strength and the corresponding axial strain of quartz sand are less than that of CCS,and the hysteresis loops between the unloading curves and the reloading curves of quartz sand are more obvious than that of CCS.Compared with that in Fig.5,it is found that there is a significant difference between the two types of sands for the isotropic loading-unloading-reloading curves.In Fig.12b,it is observed that the elastic volumetric deformation of quartz sand is considerable during the isotropic loading-unloading-reloading process.Morethan 70%of volumetric strain can recover with the reduction of the applied confining pressure.While considerable plastic deformation is generated for CCS under the same stress path.

Fig.12.Typical stress-strain curves of quartz sand (Dr=46.7%): (a) Triaxial loading-unloading-reloading shear test,and (b) Isotropic loading-unloading-reloading test.

Adopting the same measurement method for the elastic shear modulus and bulk modulus of CCS stated above,the elastic shear and bulk moduli of quartz sand are firstly measured.Furthermore,the modified Hardin formula and the proposed‘Ye formulation’are both utilized to mathematically fit these measured elastic moduli of quartz sand,as shown in Fig.13.It is found that the estimated values of the modified Hardin formula under the condition of large strain are significantly different from the measured values (R2are all less than 0.5).It means this formula cannot be applied to the estimation of the elastic shear modulus of quartz sand.It is indicated by this result that the modified Hardin formula is only suitable for the elastic shear modulus estimation when a granular material is approximately ideally elastic under the condition of small strain,and the reliability of this formula will be significantly reduced when a granular material yields to produce plastic strain.However,the proposed ‘Ye formulation’ can better estimate the elastic shear modulus of granular materials under the condition of large strain,both for CCS and quartz sands.The fitting parameters are listed in Table 8.

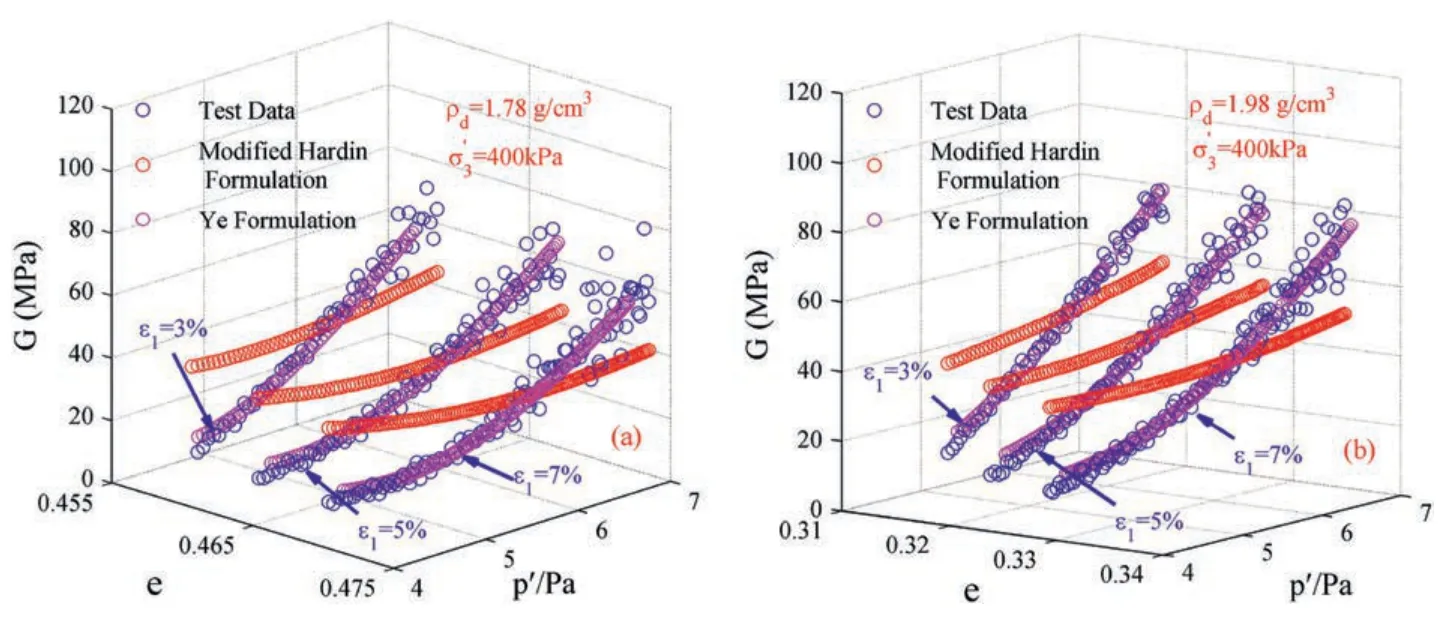
Fig.13.Comparison and validation of the elastic shear modulus of quartz sand with different estimation formulations.

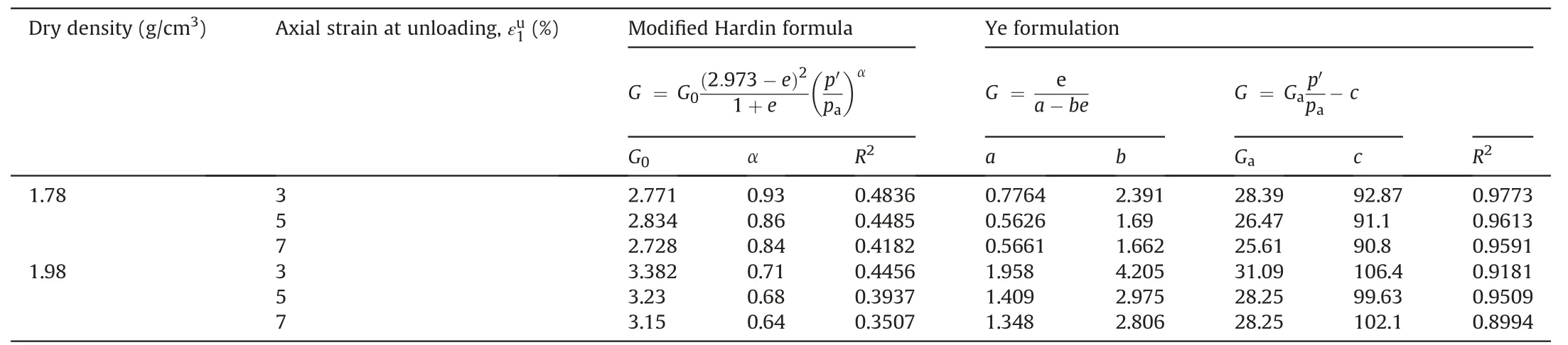
Table 8 Credibility comparison of the modified Hardin formula and‘Ye formulation’ for quartz sand.

The experimental relationship between void ratioeand mean effective principal stress lnp′of quartz sand recorded in the isotropic loading-unloading-reloading test is shown in Fig.14.Compared with that in Fig.9,it is found that the development tendency ofe-lnp′for quartz sand has little difference from that of CCS in general.The main difference is that the slope of the NCL of quartz sand basically remains constant since quartz sand particles have high particle strength and are not easy to break.However,the unloading lines in thee-lnp′space are also a series of straight lines,like that of CCS.Through mathematical fitting(as listed in Table 9),it is found in Fig.15 that both the modified Hardin formula and the proposed‘Ye formulation’have good agreement on the estimation of the elastic bulk modulus of quartz sand.

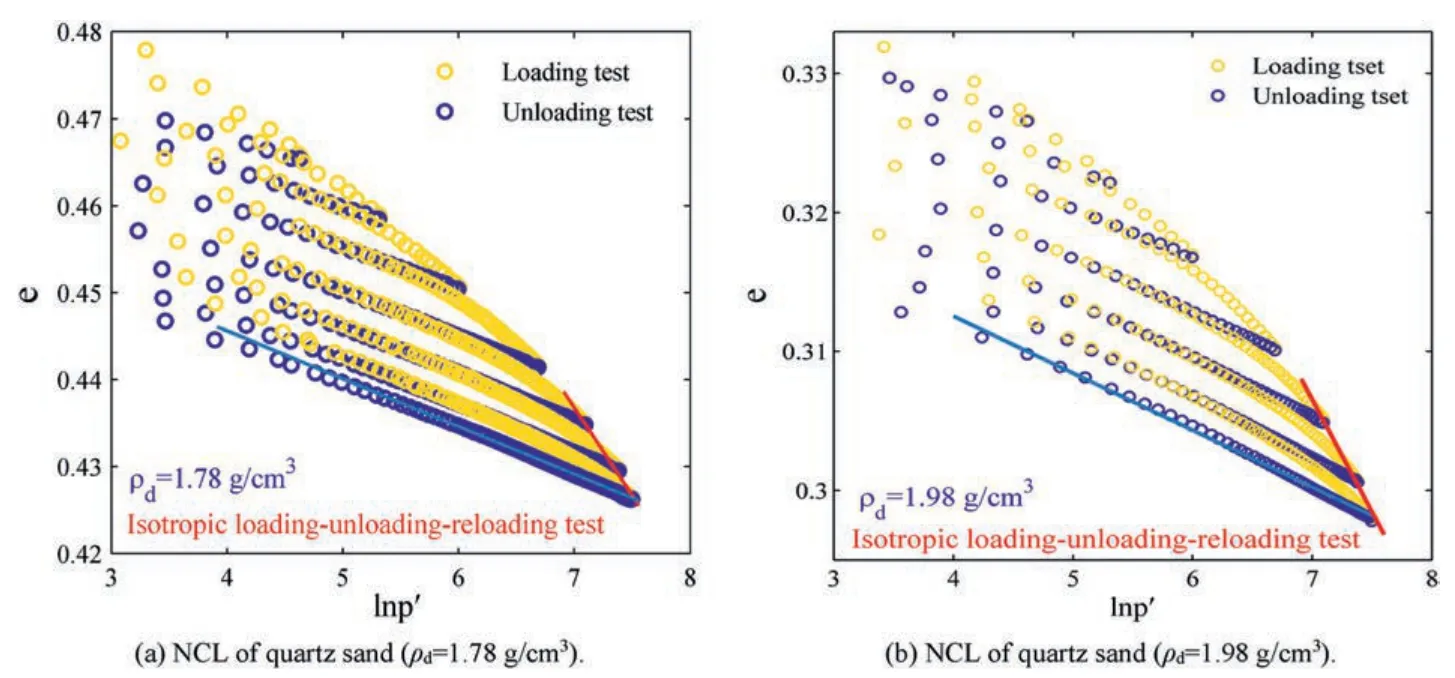
Fig.14.Typical experimental relationship between void ratio e and lnp′ recorded in the isotropic loading-unloading-reloading tests for quartz sand.

Fig.15.Comparison and validation of the elastic bulk modulus of quartz sand with different estimation formulations.

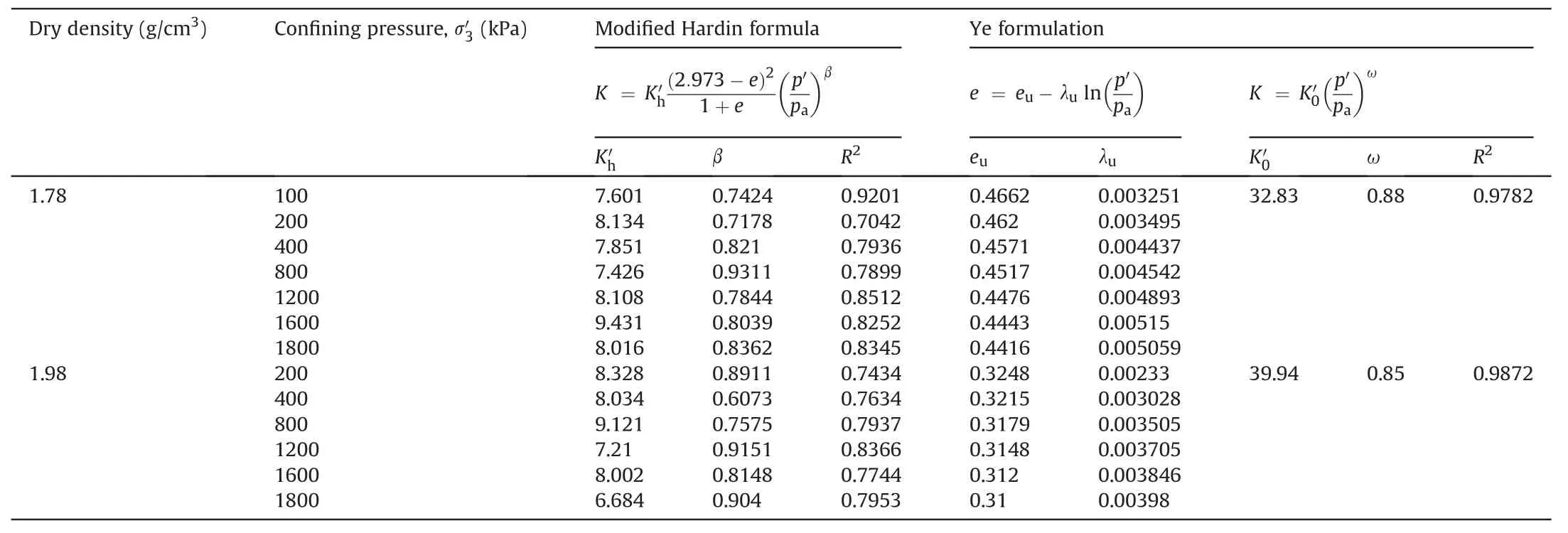
Table 9 Fitted values for the parameters in the modified Hardin formula and Ye formulation.

Summarily,it is found through comparison and verification that the modified Hardin formula is only suitable for the estimation of the elastic bulk modulus of quartz sand and CCS.While ‘Ye formulation’proposed in this study is suitable for the estimation of both the elastic shear and bulk moduli of quartz sand and CCS.

4.Conclusions

In this study,a series of triaxial loading-unloading-reloading shear tests and isotropic loading-unloading-reloading tests are conducted by taking the CCS sampled from the SCS as the test material.Based on the test results,a new set of formulae for the estimation of the elastic modulus of CCS,referred to as ‘Ye formulation’,is proposed.Through the analysis of the experimental results,the following findings are obtained in this study:

(1) It is observed that there is an obvious elastic deformation stage for CCS in the triaxial loading-unloading-reloading shear tests.The stress-strain curves at the unloadingreloading stage are almost overlapped before theelastoplastic separation point has arrived,and the hysteresis loop is very small or even absent.In the triaxial shear tests,the unloading stress-strain curves are almost parallel to each other with a great slope.Only at the end of the unloading curves,the slope gradually becomes smaller and tends to 0 when the applied confining pressure becomes less and less.

(3) Based on the experimental relationship between the elastic modulus (elastic shear modulusGand elastic bulk modulusK) and the void ratioe,mean effective principal stressp′,a new group of formulae,referred to as ‘Ye formulation’,is proposed to estimate the elastic modulus of CCS.It is also proved that this group of new formulae have better reliability and suitability than the modified Hardin formulae.It is not recommended to use the Hardin estimation formula in the development of the constitutive models for CCS,due to its poor performance comparing with test data for the elastic shear modulus.The proposed ‘Ye formulation’ for the estimation of the elastic modulus of soil provides a new idea and method for the purpose of a more accurate description of the mechanical properties of soils,especially for CCS.It will have certain significance to the estimation of,as well as research on the elastic modulus of soils,especially sandy soils.

(4) Through comparative tests for CCS and quartz sand,it is confirmed that the modified Hardin formula is only suitable for the estimation of the elastic bulk modulus of quartz sand and CCS,while ‘Ye formulation’ proposed in this study is suitable for the estimation of both the elastic shear and bulk moduli of quartz sand and CCS.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgments

Professor Jianhong Ye is grateful for the funding support from the National Key Research and Development Program of China(Grant No.2022YFC3102402).

List of symbols

GElastic shear modulus

Ψ,α,kMaterial-related dimensionless parameters

OCROver-consolidation ratio of soil

eVoid ratio of soil

p′Mean effective principal stress of soil

paAtmospheric pressure

BSkempton’sBvalue,pore pressure coefficient

A(γ),n(γ) Material parameter correlated with shear strain γ

CuCoefficient of uniformity of soil

CcCoefficient of curvature of soil

FcFines content of soil (%)

D50Mean particle diameter of soil

ρdDry density of soil

ρmaxMaximum dry density of soil

ρminMinimum dry density of soil

GsSpecific gravity of soil particles

εrRadial strain of soil

εaAxial strain of soil

EYoung’s modulus

ν Poisson’s ratio

a,b,cFitting parameters

εvVolumetric strain of soil

σuThe stress at the elastoplastic separation point

KElastic bulk modulus

K0The elastic bulk modulus of soil whenp′=pa

λ The slope of the NCL of soil

eΓ The void ratio of soils whenp′=1 kPa

P1,P2,P3Material-related parameters

λpThe compression index where the confining pressure isp′

λuThe slope of the unloading lines

euThe void ratio when confining pressure is unloaded top′=pa

R2Correlation coefficient

e0Initial void ratio of soil

ΔeVariation of void ratio