Failure characterization of fully grouted rock bolts under triaxial testing
Hai Nourizah,Ali Mirzaghoranali,Mhi Srati,Elamin Mutaz,Kvin MDougall,Naj Aziz
a Centre for Future Materials (CFM), School of Engineering, University of Southern Queensland, Toowoomba, QLD, 4350, Australia
b School of Engineering, University of Southern Queensland, Springfield Central, QLD, 4300, Australia
c School of Civil Engineering, University of Queensland, St Lucia, QLD, 4072, Australia
d School of Surveying and Build Environment, University of Southern Queensland, Toowoomba, QLD, 4350, Australia
e School of Civil, Mining &Environmental Engineering, University of Wollongong, Wollongong, NSW, 2500, Australia
Keywords: Rock bolts Bolt-grout interface Bond strength Push test Triaxial tests
ABSTRACT Confining stresses serve as a pivotal determinant in shaping the behavior of grouted rock bolts.Nonetheless,prior investigations have oversimplified the three-dimensional stress state,primarily assuming hydrostatic stress conditions.Under these conditions,it is assumed that the intermediate principal stress(σ2) equals the minimum principal stress (σ3).This assumption overlooks the potential variations in magnitudes of in situ stress conditions along all three directions near an underground opening where a rock bolt is installed.In this study,a series of push tests was meticulously conducted under triaxial conditions.These tests involved applying non-uniform confining stresses (σ2 ≠σ3) to cubic specimens,aiming to unveil the previously overlooked influence of intermediate principal stresses on the strength properties of rock bolts.The results show that as the confining stresses increase from zero to higher levels,the pre-failure behavior changes from linear to nonlinear forms,resulting in an increase in initial stiffness from 2.08 kN/mm to 32.51 kN/mm.The load-displacement curves further illuminate distinct post-failure behavior at elevated levels of confining stresses,characterized by enhanced stiffness.Notably,the peak load capacity ranged from 27.9 kN to 46.5 kN as confining stresses advanced from σ2=σ3=0 to σ2=20 MPa and σ3=10 MPa.Additionally,the outcomes highlight an influence of confining stress on the lateral deformation of samples.Lower levels of confinement prompt overall dilation in lateral deformation,while higher confinements maintain a state of shrinkage.Furthermore,diverse failure modes have been identified,intricately tied to the arrangement of confining stresses.Lower confinements tend to induce a splitting mode of failure,whereas higher loads bring about a shift towards a pure interfacial shear-off and shear-crushed failure mechanism.
1.Introduction
The stability of underground excavations is a primary concern for geotechnical and mining engineers seeking to improve workers safety,reduce environmental issues,and avoid financial loss.Rock bolts are generally considered the most adaptable and efficient reinforcement system in complex ground conditions(Li,2017).The response of rock bolts to excitation or disturbance depends on the type of bolt,bolt arrangement in the field,and the mode of the subjected force,which can be predominantly shear,axial,or flexural (Chen,2014;Li et al.,2014,2019).However,the typical behavior is likely a combination of all the forces above (He et al.,2017).
The impact of surface geometry,identified by the bolt rib angle,height,spacing,width,and orientation,has been studied experimentally and numerically to optimize bolt performance (Aziz and Webb,2003;Kılıc et al.,2003;Yokota et al.,2019;Cui et al.,2020).Grout acts as a medium for transmitting initiated stress from the bolt to the stable rock mass,and also to transfer the in situ stress from the surrounding rock to the bolt-grout interface.The interaction between the mechanical characteristics of the grout and rock bolt behavior has been well studied by many scholars who agree with the positive effects of stronger grouts on bolting performance (Kılıc et al.,2002;Li et al.,2016;Yu et al.,2019;Høien et al.,2021;Nourizadeh et al.,2021).The bolt diameter and mechanical properties also affect the axial behavior of rock bolts(Chen et al.,2020).The process of bolt installation can also significantly impact the quality of encapsulation,consequently influencing the bond strength of the reinforcement system.Aziz et al.(2016)comprehensively studied the effects of grout thickness,borehole diameter,and resin mixing procedure via field and laboratory pullpush out tests.In the study by Ma et al.(2017),it was identified that improper mixing of resin components leading to the presence of gloving and air bubbles can markedly diminish the load-bearing capacity of sections spanning the encapsulation length.Furthermore,efforts have been undertaken to quantify the impact of bolt concentricity on anchoring capacity(Fu et al.,2019;Liu et al.,2020).These investigations were accompanied by innovative approaches leading to better resin mixing.Notably,achieving an optimal grout annulus thickness is a pivotal consideration,within practical constraints (Fabjanczyk and Tarrant,1992;Fuller and O’Grady,1994).The critical embedment length refers to the minimum grouted length of a specific rebar that has an anchorage strength greater than the yielding strength of the bolt.This length depends on the bond characteristics at the bolt-grout interface,uniaxial compression of grouts,and elastic-plastic behavior of the steel rod(Li et al.,2016;Høien et al.,2021).
Furthermore,the rock mass characteristics can heavily influence the critical failure mechanism,failure location,and bond stiffness in the design of rock bolt systems(Salcher and Bertuzzi,2018;Hazrati et al.,2020).The axial slip of deformed reinforcing elements causes radial dilation,which is limited or inhibited by the rock mass’s normal stiffness.A higher normal stiffness can lead to higher induced lateral confining stress and higher interfacial bond strength (Hyett et al.,1992;Yazici and Kaiser,1992).
In situ stress has a crucial role in the failure mode of an excavation(Li,2017).Conversely,external confining stress can enhance the performance of rock bolts (Blanco et al.,2013).Therefore,it is essential to carefully consider the effect of in situ stresses on the behavior of rock bolts for their design.Hyett et al.(1995)conducted a series of pull-out tests using modified Hoek cells under constant confining pressures.The experimental results indicated that the bond strength increases with confining pressure.In a study conducted by Thenevin et al.(2017),an array of pull-out tests was undertaken,with a distinct focus on the impact of confinement pressure.These tests were executed under two conditions: constant radial stiffness and constant radial load.This was accomplished using a triaxial cell with confining pressures extending up to 15 MPa.The outcomes of this investigation align with previous research,highlighting that elevated confining pressures yield a heightened peak bond strength.Kang et al.(2020)pointed out that,in practice,rock bolts are typically subjected to complex loading conditions rather than a simple pull-out load,significantly affecting their behavior.Apart from experimental studies,analytical and numerical models have also been developed to investigate the effect of confining stress on the axial behavior of rock bolts.Li et al.(2021) developed an analytical model based on the modified continuously yielding criterion to analyze the performance of rock bolts under constant confining pressure.However,this model is only suitable for uniform constant confining pressure and cannot be applied to other boundary conditions.Similarly,the failure models developed by Blanco et al.(2013),Ho et al.(2019)and Chen et al.(2020)also assume uniform confining stress conditions.
The studies mentioned above possess certain limitations when it comes to comprehending the behavior of fully grouted rock bolts under varying confining pressure conditions.The stress state surrounding underground openings is non-uniform and can differ significantly in different areas of a rock mass.This non-uniformity may result in variations in the mechanical response of rock bolts that cannot be captured by previously developed models.This paper qualitatively discusses an experimental study in which rock bolts embedded in cubic specimens of concrete were tested under triaxial stress conditions to address these limitations.Understanding the impact of confining stresses on rock bolt behavior by simulating actual in situ conditions can effectively inform the design and construction of more efficient and reliable rock support systems,leading to safer and more efficient underground excavations.The study investigates the interaction between confining stresses and the principal stress ratio (k=σ2/σ3) and interfacial bond strength.It should be noted that planes of zero shear stress were considered in the test design,where the normal stress components become principal(τxy=τyx=0,σx=σ2,σy=σ3).Finally,the lateral displacement associated with the outer surfaces of the cubic specimen during push-out was analyzed.The results of this experimental study will contribute to a better understanding of the behavior of rock bolts under real ground conditions where varying levels of confining stresses are present.This advancement is expected to contribute to the development of designing,modeling,and application of strata control in underground openings.
2.Experimental program
The methodology utilized in this study involves the preparation of cubic concrete specimens as a simulated rock mass.Deformed rebars were subsequently installed and encapsulated in holes created in the center of the cubic specimens.Finally,push-out tests were conducted using a state-of-the-art true triaxial testing machine to investigate the behavior of rock bolts under varying triaxial conditions.
2.1.Specimen preparation
Short encapsulation (SE) was utilized to investigate debonding mechanisms of rock bolts.To prepare the surrounding material,concrete was mixed according to the design proposed by Serati et al.(2020),cast in a larger rectangular prismoidal mold,and kept in a moist room.After 70 d of curing,the concrete was cut into smaller specimens with dimensions of 60 mm×60 mm×37 mm(L×W×H).The specimens were trimmed,and a central hole with a diameter of φ35 mm was cored.M24 X Coal Bolt manufactured by Minova Australia was cut into equal-length pieces of 50 mm.The bolts were then centrally encapsulated in the hole using Stratabinder HS,a widely used cementitious grout in Australia produced by Minova Australia.Table 1 presents the mix design of the concrete and grout used in the sample preparation.
2.2.Experimental equipment
The primary method commonly used to investigate the behavior of rock bolts is to conduct pull or push tests,although both methods do not fully replicate field conditions (Cao et al.,2013).Recently,new deep learning methods have been developed to estimate the pull-out strength of anchors(Kovaˇcevi′c et al.,2021;Saleem,2020).Previous research has indicated that,typically,the bearing capacity of bolts subjected to push tests tends to surpass that of bolts subjected to pull-out tests.However,these variations hinge on factors such as the materials employed and the specific testing methodologies adopted (Aziz et al.,2006).Nevertheless,the push-out approach can provide a good understanding of the behavior of reinforcing elements (Hyett et al.,1992).The current study employed push tests using a true triaxial testing facility at the Rock Mechanics laboratory of the Geotechnical Engineering Centre at the University of Queensland(UQ,Australia).The system can apply up to 850 kN of force on a wide range of cubic samples ranging from50 mm to 200 mm in size.It can also simulate stress conditions at elevated temperatures of up to 100°C for hydraulic fracturing and coupled thermo-hydro-mechanical testing on rock-like specimens(Fig.1).To accurately measure the specimen volume change,each of the six actuators of the machine is equipped with three linear variable differential transformers (LVDTs).This LVDT system enables the measurement of deformation and displacement of tested rock bolt samples to calculate the average lateral dilation and bolt slippage (Purser et al.,2021).In this study,cubic specimens were placed on the pressure plates and confined from both theXandYdirections,as shown in Fig.1.

Fig.1.The experimental setup used in this study,which includes (a) the true triaxial testing facility,(b,c) the arrangement of the chamber,pressure plates,pistons,and cubic specimens,(d) the dimensions of the specimens,and (e) the rock bolts used in the experiments.
For consistent and even loading,it is essential to accurately position the specimens by periodically verifying the testing setup.This involves ensuring that the pressure plates maintain contact with the specimen’s surface.Any displacement of the specimen can lead to uneven loading,underscoring the importance of maintaining proper positioning.To create space for bolt slippage,a 12 mm thick steel spacer with a central hole of φ30 mm was positioned under the specimen on theZ1 side.The pressure plate on theZ2 side was then placed on the bolt and pushed at the desired rate.Fig.1 also illustrates the dimensions of the specimens and the materials used in the experiments.
A series of triaxial push tests was undertaken on a total of 12 specimens.These tests were designed to analyze the response of grouted rock bolts under diverse confinement conditions.The mechanical attributes of both the concrete and the grout were determined through uniaxial compression tests (UCS),with the resultant values documented in Table 2 along with the specifications of the rock bolts.Non-destructive methods can also be applied to obtain the mechanical characteristics of materials (Azarafza et al.,2022).

Table 2 Mechanical properties of the materials.
To accurately analyze the influence of confining stress on the bolts subjected to a push-out force,four varying minor principal stresses (σ3) with the values of 0,2.5,7,and 10 MPa were applied.The intermediate principal stresses (σ2) were selected so that the ratio of intermediate principal stress to minor principal stress (k)was approximately 1,1.5,and 2.To assess the validity of the measures,some of the tests were repeated.Table 3 specifies the confining stress program applied to the tests.
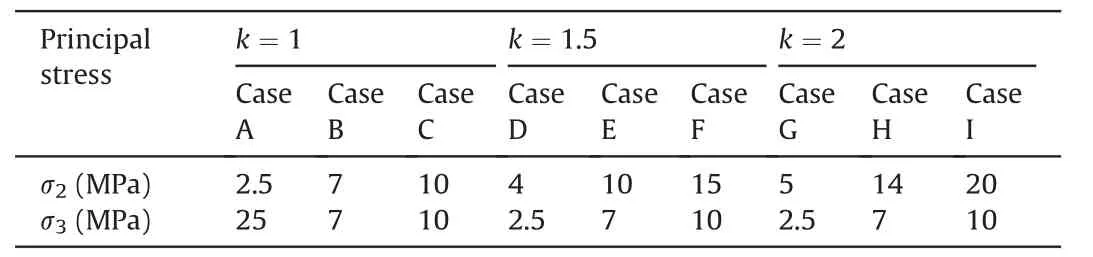
Table 3 Confining stress campaigns in the testing programs.
The cubic specimen was placed on the pressure plate on theZ1 side,and then the pistons were adjusted so that the pressure plates touched the surface of the specimen in theX1,X2,Y1,andY2 directions.An initial load of 3 kN (referred to as seating load) was applied to the specimen in all directions.The loads in theXandYdirections(hereafter referred to asX-Load andY-Load,respectively)were then increased hydrostatically at a rate of 3 kN/min until reaching 5 kN.After that,the loading rate was increased to 15 kN/min until theX-pressure reached the value of (σ3).Subsequently,the load in theX-direction was maintained at a constant level,while theY-load was increased until it reached the predetermined value of σ2.When both theX-andY-loads exceeded 5 kN,the pistons in theZ2direction began applying load at a rate of 5 kN/min until the bolt debonded.Fig.2 shows a typical loading program for the testing.

Fig.2.A typical subjected load program on the specimens.
The mechanical behavior of a grouted reinforcing element under axial loading is governed by the bond mechanism.Bond strength refers to the shearing resistance between the reinforcing element and grout.In rock bolting,bond strength can be described as the gripping effect of grout on the deformed bar’s encapsulated length(Moosavi et al.,2005).The bond strength is generally considered a function of three components,namely adhesion between the grout and bolt,friction,and mechanical interlocking between bolt ribs.Before system failure (peak bond strength),mechanical interlocking plays a crucial role in the system bond capacity.Interlocking is dependent on the mechanical properties of grout materials,rock mass conditions,level of confining stress,and bolt surface configuration (Cao et al.,2013;Cui et al.,2020).
Fig.3 illustrates the stress equilibrium for an encapsulated rock bolt at infinitesimal length delwhen subjected to a tensile stress of σb+dσb.It has been shown that bond strength is a function of confining stress,bolt surface configuration,grout and surrounding media quality.If slip failure at the bolt-grout interface is taken into consideration,the induced bond stress at the bolt-grout interface(fbu) can be expressed as

Fig.3.Stress equilibrium of infinitesimal embedded rock bolt.
whereDbis the effective diameter of the bolt,dσbis the increment of tensile stress on the bolt,and delis the infinitesimal length of the bolt.
Studies have shown that the bond stress distribution along the embedment length of a long-anchored reinforcement is nonuniform and decreases towards the free end (Vlachopoulos et al.,2018).However,the average bonding stress can be effectively used for short embedment specimens.The normalized induced bond stress can be used as a strength criterion to analyze the axial behavior of bolts,especially in cases where different encapsulation lengths or bolt diameters are used.The average bonding stresscan be calculated by
whereFbuis the peak push load in theZ2 direction,elis the encapsulation length (which is 37 mm in this study),andsis the bolt slip.However,since the bolt encapsulation length during testing is constant,scan be considered zero.
3.Experimental results and discussion
Confining stress stands as a pivotal factor influencing rock bolt behavior.Within underground openings,stresses might not uniformly manifest across all directions,underscoring the significance of scrutinizing rock bolting systems within authentic conditions.Despite this,the impact of deviatoric stress (σ2≠σ3) on the response of fully-grouted rock bolts has,to the authors’knowledge,largely been overlooked within the existing literature.The experiments reported in this paper were designed and conducted to investigate the behavior of fully-grouted rock bolts under biaxial confining conditions.The testing equipment used in this study the capability to record the necessary data for a comprehensive mechanical investigation,including load and displacement in three mutually perpendicular directions(X,Y,Z)with high accuracy.The outcomes derived from these experiments served as the foundation for the analysis of various aspects,encompassing axial behavior,interfacial bond strength,deformation characteristics of the adjacent media,and the mechanism of system failure.
3.1.Push force and bolt slip relationship
The load-displacement relationship is a common approach for analyzing the behavior of fully grouted rock bolts.Various linear,nonlinear,and combined analyses have been presented for evaluating the performance of fully grouted rock bolts (Li and Stillborg,2000;Ren et al.,2010;Martín et al.,2011;Ma et al.,2013;He et al.,2015;Bahrani and Hadjigeorgiou,2016;Jahangir et al.,2021;Yue et al.,2022).A typical load-displacement model is shown in Fig.4,which can be characterized by three distinct stages:

Fig.4.A typical load-displacement curve for encapsulated rock bolt(with and without confining stress) (after Yeih et al.,1997).
(1) A quasi-linear increase in the curve where the stiffness (the ratio of axial load to displacement)is constant,and the loaddisplacement response is in an elastic stage.
(2) An ascending curve where the axial load increases with slip until reaching the maximum load value,although the stiffness slightly decreases.It has been reported that debonding of rock bolts starts during the transition from stage 1 to stage 2 (Høien et al.,2021).
(3) A descending curve where the axial load decreases with bolt slip.
The load-slip curves of the tested specimens,which have the same embedment length and materials but different confining conditions,are presented in Fig.5a-c,corresponding to the tests conducted with principal stress ratios of 1,1.5,and 2,respectively.The results clearly indicate that the confining stresses have a significant strengthening effect on the samples.It can be observed that the axial load increases as slip increases from the beginning until reaching the peak load,after which it begins to decline.The curves generally consist of three stages,similar to Fig.4: an initial linear growth,followed by a nonlinear ascending curve,and finally a strain softening stage.However,the increase in confinement stresses results in four primary changes in the resulting load-slip curves.Firstly,the transition from linear to nonlinear behavior occurs at lower slip magnitudes.Secondly,the stiffness in the linear elastic part increases significantly with higher confining stresses.Thirdly,the ultimate bearing capacity is influenced by the level of confinement.Finally,the peak load is attained at larger slip values.The load-slip curve can be classified into two main categories based on the pre-peak load-slip characteristics of the push-out tests,which are used to establish linear-nonlinear transformation models.In the cases where there are zero or low confining stresses(Fig.5a),the failure mode resembles a brittle failure,exhibiting a distinct peak bond strength accompanied by strain-softening behavior.However,at higher confining stresses,failure exhibits a slight ductility,and the axial slip corresponding to the failure point tends to have higher magnitudes,followed by the occurrence of softening behavior.At σ2=σ3=0,the load-slip curve initially shows linear growth until the load reaches 25.4 kN,which corresponds to 91%of the ultimate bearing capacity.This is followed by a nonlinear plastic phase until reaching the ultimate strength,and finally a sharp drop.In the case where σ2=σ3=2.5 MPa,the linear elastic section transforms into a nonlinear curve when the load reaches 20.8 kN,equivalent to 72%of the ultimate strength,despite the peak load being only 3.5%higher compared to the case without confinement.As depicted in Fig.5,the nonlinearity of the load-slip curves expands with an increase in confining stresses.In cases with a higher level of confining stresses (e.g.σ2=15 MPa,σ3=10 MPa and σ2=20 MPa,σ3=10 MPa),it becomes challenging to distinguish the linear portion.Consequently,the load-slip behavior can be characterized by a progressively nonlinear elastic-plastic response.Yeih et al.(1997) discussed the failure modes for rebars with and without confinement and concluded that confining force affects the peak load and the post-failure mechanism,while the pre-failure behavior is not affected.An experimental study conducted by Moosavi et al.(2005) reported the same statement and showed that the load-displacement curves overlap moderately before yielding points.Thenevin et al.(2017) demonstrated that elevating the confining stress leads to increased stiffness and peak load.However,it is important to note that the overall shape of the load-displacement curve remains unchanged despite these variations.Therefore,the results of the current study demonstrate that,in higher levels of confining stress,nonlinear bond models are more suitable;however,in the lower level of confinement,a combined linear and nonlinear model can be adopted.As opposed to the test without confining stress,the post-failure behavior of the tests with confining stress illustrates a smooth and progressive softening phase.Analyzing the bolt-slip curves also shows that the softening part of the curves becomes flatter in the cases with higher confining stresses(Fig.5b and c).The main reason for this is the existence of the high level of confinement,and thus,the surrounding materials and grout can resist cracking and dilation.Also,the normal force at the bolt-grout interface causes a secondary interlocking after the main failure,thereby holding the bolt against the push load.

Fig.5.Load-slip curves obtained from the tests conducted at three different principal stress ratios(k=σ2/σ3): (a) k=1,(b) k=1.5,and (c) k=2.
Expectedly,the bond capacity of specimens rises as the confining stresses increase.For instance,in the absence of confinement,the peak push load was measured 27.9 kN,whereas it increased to 28.9 kN,36.3 kN,and 38.7 kN with uniform confining stresses(σ2=σ3)of 2.5 MPa,7 MPa,and 10 MPa,respectively.The same trend is observed for tests conducted withkvalues of 1.5 and 2,where the peak loads increase with the confining stress.However,some differences are visible in the pre-and post-failure phases,as discussed earlier.In the descending part of the loadslip curve,the rate of load decrease becomes slower with increasing confinement,thus the slope of the load-slip curve decreases.The linear approximation and averaging determines the slope of the curves in the post-failure stage to be 4.4,3.7,3.1,2.9,1.2 and 1.1 kN/mm for the tests conducted with σ2=σ3=0 MPa,σ2=σ3=2.5 MPa,σ2=σ3=7 MPa,σ2=14 MPa and σ3=7 MPa,σ2=15 MPa and σ3=10 MPa,and σ2=20 MPa and σ3=10 MPa,respectively.Lower magnitudes of the slope indicate higher frictional resistance of the system against bolt slip.Thus,it can be concluded that the post-failure strength is improved with confinement.The slip corresponding to the maximum bond strength increases with higher levels of confinement.Conversely,the slope of the descending section of the curves immediately after the peak load decreases as the confinement increases.Therefore,it can be concluded that confining stresses significantly enhance the ductility of the samples.For the specimen without confinement,the displacement corresponding to the peak load was 6.3 mm,whereas the peak load displacement shifted to the right with an increase in confining stress,reaching 10.3 mm for the specimen subjected to the highest confining stresses (σ2=20 MPa,σ3=10 MPa).Table 4 presents the peak loads and corresponding slips for the tested specimens.The fluctuations observed in the ascending phase of the graphs can be attributed to lateral deformation and specimen dilation caused by bolt slip during the push-out process.These fluctuations are consistent with the variations observed in the force-time and displacement-time data recorded by the sensors in theXandYdirections (as shown in Fig.2),indicating that the sensors on the lateral pistons require some time to adjust the confining stresses to the predefined values.Additionally,localized failure and damage occurring in the area near the loading point may also contribute to these fluctuations.
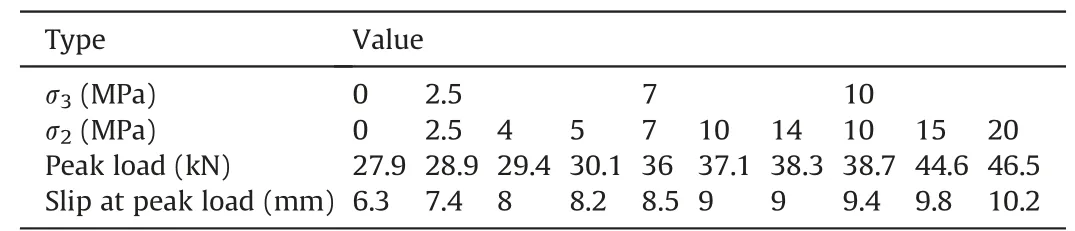
Table 4 Peak load and corresponding slip for the tests.
Stiffness is a crucial parameter for characterizing the load-slip performance of rock bolts subjected to a tensile load (Li et al.,2021).In rock bolting,stiffness is defined as the derivative of the load-slip curve with respect to the slip.Fig.6 shows the stiffnessdisplacement curves for the case with σ2=σ3=0 MPa and the cases wherek=2.The figure indicates that the stiffness (i.e.the slope of the load-displacement curve) for confined specimens decays exponentially before final failure occurs,while the stiffness for the specimen without confining stress increases until 0.5 mm of displacement followed by a gradual decrease until the system fails.Among all specimens,the specimen without confinement(σ2=σ3=0)showed the minimum shear stiffness(2.08 kN/mm)at the beginning of the push-out tests.The initial shear stiffness was also calculated as 24.08 kN/mm,28.07 kN/mm,and 32.51 kN/mm for the tests conducted with σ2=5 MPa and σ3=2.5 MPa,σ2=14 MPa and σ3=7 MPa,and σ2=20 MPa and σ3=10 MPa,respectively.Moreover,it is evident from the results that the stiffness of the confined specimens is significantly higher than that of the unconfined specimen during the initial stages of the testing.However,in certain degrees of displacement,the rigidity of the unconfined test slightly surpasses that of the confined tests.The abrupt decrease in stiffness for the unconfined specimen indicates a brittle ultimate failure,unlike the failure of specimens with confining stresses,which exhibits a semi-ductile behavior.Based on the presented results,it can be concluded that for confined specimens,the ultimate failure can be anticipated when the stiffness reaches approximately 1 kN/mm,regardless of the level of confinement.
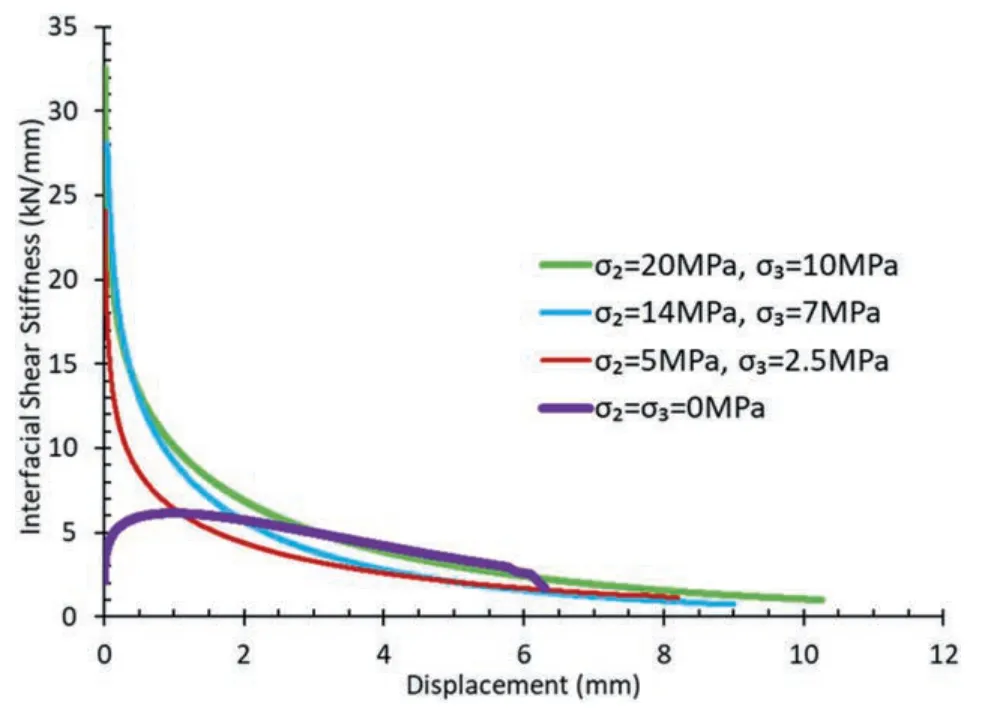
Fig.6.Interfacial shear stiffness of the tests from beginning to the peak capacity for the test without confining stress and the tests with k=2.
3.2.Relationship between confining stress and interfacial peak bond strength
Fig.7 shows the influence of the intermediate principal stress on the resultant interfacial bond stress of the system as a function of the principal stress ratio (k).As illustrated,the interfacial bond stresscalculated using Eq.(2) increases linearly with the intermediate principal stress(σ2)at allkratios.However,when σ2is kept constant,the bond stress is lower at higherkratios.Interestingly,it was found that the bond stress in tests with σ2=σ3=7 MPa is equal to that of the test with σ2=10 MPa and σ3=7 MPa,whereis 13.4 MPa.Fig.7 also demonstrates that the impact of the principal stress ratio onis more significant at higher values of σ3.For instance,the difference between the bond strengths of points (a) and (b),where σ3=2.5 MPa,is 0.21 MPa,while this difference increases to 0.65 MPa when σ3reaches 10 MPa (bond strength difference between points (c) and (d)).Additionally,it is observed that the trend lines(grey round-dot lines)increase slowlywith an increase in σ2,indicating a lower impact ofkat higher levels of σ2compared to lower levels.It can be postulated that after a certain value of σ2and at the specified level of σ3,interfacial bond strengths either remain constant or deteriorate.Further research with a higher level of confining stresses is required to effectively evaluate this hypothesis.

Fig.7.The effects of confining stresses on the bond strength.Blue,red and black trend dashed lines indicate changes in the interfacial bond stress with respect to σ2 at the principal stress ratios (k=σ2/σ3) equal to 1,1.5 and 2,respectively.Grey dashed curves represent the variation ofwith σ2 at σ3=2.5,7 and 10 MPa (from bottom to top).
According to the test results,the bond strength at the bolt-grout interface increases linearly with σ2for a certain ratio of principal stresses (k) (Fig.5).Similarly,higher values of σ3amplify the bearing capacity of the rock bolts.This statement is supported by continuously yielding criteria that have been employed in numerous analytical models.These models showcase that shear stiffness experiences enhancement as the normal force increases(Li et al.,2021).The results forkequal to 1 are consistent with previous studies.Thenevin et al.(2017)concluded that an increase in the confining pressure leads to a linear increase in peak pull-out force,and Moosavi et al.(2005) found an ascending linear relationship between bond capacity and confining pressure.Furthermore,at a specific level of σ2,the specimen can withstand higher push loads in hydrostatic stress conditions compared to those withkvalues of 1.5 and 2.The adapted curves for any individual magnitude of σ3(grey dotted lines)show a logarithmic trend,asinitially grows rapidly with σ2and then flattens.Based on the results and curves,it is anticipated that at a specific level of σ2,may reach a maximum value followed by a marginal descending trend regardless of σ3.
3.3.Response of the surrounding medium to bolt slip under biaxial confinement
The axial slip of deformed reinforcing elements generates radial dilation as a response to the induced radial stresses,which is inhibited or restricted by the normal stiffness of the rock mass and the state of confining stresses.The degree of radial displacement of the surrounding media is influenced by the surface geometry of the bolt.Splitting of grout is rare for round bars,highlighting the significance of bolt surface geometry.The dilation of the specimen in theXandYdirections was recorded with high accuracy using several displacement sensors.The results demonstrate a strong correlation between the state of confining stress and the level of dilatation.Deformations normalized to the specimen dimensions in both theXandYdirections can be employed to examine the influence of confining stresses on the lateral deformation of specimens during push-out tests,as described by Eqs.(3) and (4).
whereexandeyare the principal relative deformations in the σ2and σ3,respectively;dxanddyare the sums of deformations recorded by LVDTs inX1,X2andY1,Y2directions,respectively;andlxandlyare the dimensions of the specimens inXandYdirections,respectively.
Fig.8 shows the incremental relative deformation of the specimens in theXandYdirections(ex,ey,exy)with respect to the push load for the tests with σ2=σ3=0 MPa,σ2=σ3=2.5 MPa,σ2=σ3=10 MPa,and σ2=20,σ3=10 MPa,respectively.A positive value indicates shrinkage of the specimen,while a negative value indicates dilation.In the case without confinement,exgradually decreases once the push load is applied,whileeydoes not experience a visible change until the push load reaches 15 kN.Thereafter,expansion occurs in both directions with the load,and finally,exandeyreach -11.98% and -3.8%,respectively,corresponding to 7.1 mm and 2.3 mm displacement.This magnitude of dilation is enough to disintegrate the specimen,as can be seen in Fig.9.Failure due to dilation has been indicated numerically as the main failure mode in rock bolting (Shi et al.,2022).The lateral deformation response of the specimens is different when the confining stress is applied.As shown in Fig.8,firstly,the specimens shrink to a certain level of push load (which increases with the increase of the confining stresses),followed by expansion,and then the lateral deformation increases again somewhat.The initial shrinkage is associated with the continuous increase in σ2and σ3,while the expansion of the specimens is due to the dilational force induced by the bolt slip at the bolt-grout interface.It should be noted that the initial relative deformation shown in the graphs is due to the primary confining stress applied before starting push loads.The results demonstrate that in lower levels of confinement,dilation is much higher.For instance,in the test with σ2=σ3=2.5 MPa,the slip of the bolt causes a maximum of-0.052%dilation occurring at the peak load,while when the confining stresses increase to σ2=σ3=10 MPa,the dilation phase was not detected,and the specimen was always in the shrinkage stage.Nevertheless,the slip of the bolt heals the shrinkage magnitude in both directions somewhat.
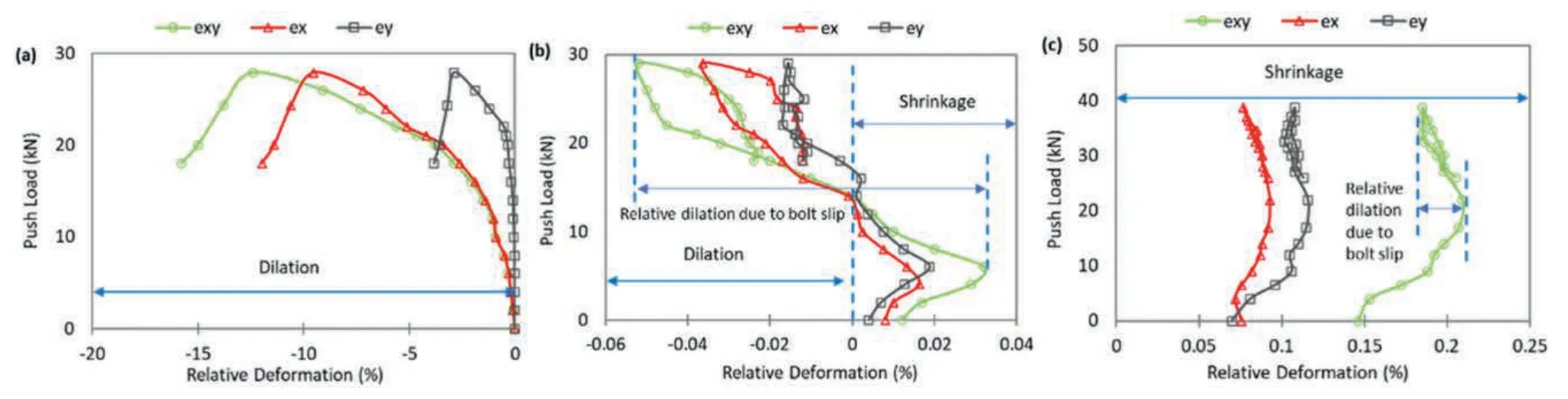
Fig.8.Deformation of the lateral surfaces of the specimens when (a) σ2=σ3=0 MPa,(b) σ2=σ3=2.5 MPa,and (c) σ2=σ3=10 MPa.

Fig.9.Fractures in the specimen under no confinement condition.
As shown in Fig.8,in all cases,the degree of dilation in theXdirection is higher than that in theYdirection.The reason is associated with the rib configuration along the bolt.As shown in Fig.10,the bolt is manufactured with two types of ribs: the transversal ribs and the longitudinal ribs.The longitudinal ribs only extend in theYdirection and along the bolt with the width and height of 1.5 mm and 0.5 mm,respectively.However,the transversal ribs are designed and manufactured throughout the circumference of the bolt core so that the rib height decreases from 1.5 mm in theXdirection to 0.5 mm in theYdirection (see the cross-section view in Fig.10).Therefore,once the bolt slips,a higher level of bond stress and normal force is produced in theXdirection compared to that in theYdirection.

Fig.10.Surface profile characterization of the rock bolt.
The total measured deformation (exy) against bolt slip for all tests is presented in Fig.11.Regardless of the level of confining stress,all graphs in Fig.11 follow a similar pattern which can be divided into four distinct sections.Firstly,there is a sharp rise where there is no pushing load,but σ2and σ3increase simultaneously.Then,exyincreases with bolt slip,but with less intensity compared to the previous section.This may be due to the fact that the induced dilation starts to confront the created compressive deformation by σ2and σ3.Lateral deformation slightly inclines with bolt slip followed by a rise till testing finishes.In the lowest confining stress (σ2=σ3=2.5 MPa),the relative lateral deformation(exy)initially undergoes a small level of shrinkage and then the specimen deforms outward due to the bolt slip once the bolt displacement reaches 0.55 mm.The lateral deformation of the artificial rock overtakes zero at around 4 mm of bolt displacement and reduces to around-0.05%at 7 mm of displacement,indicating that the unbound stress at the bolt-grout interface increases with bolt slip.The specimen then experienced a gradual shrinkage stage and finallyexysettled at around -0.02% at 12 mm of bolt displacement.From the lateral deformation,it can be concluded that the bolt-grout interface is partially damaged,and consequently,the specimen showed contractional behavior.Similar behavior can be observed in all tests with different intensities of contraction and dilation.For instance,in the case with σ2=20 MPa,σ3=10 MPa,exyinitially reached +0.24% at the desired confining stress,dropped to+0.212%,and then increased to+0.252%.As can be seen,unlike the previous case,theexyrate at the end of the test(+0.252%)is higher than the one at the starting point(+0.24%)due to the extensive damage at the bolt-grout interface in higher loads.In conclusion,following conclusions from these graphs are drawn:
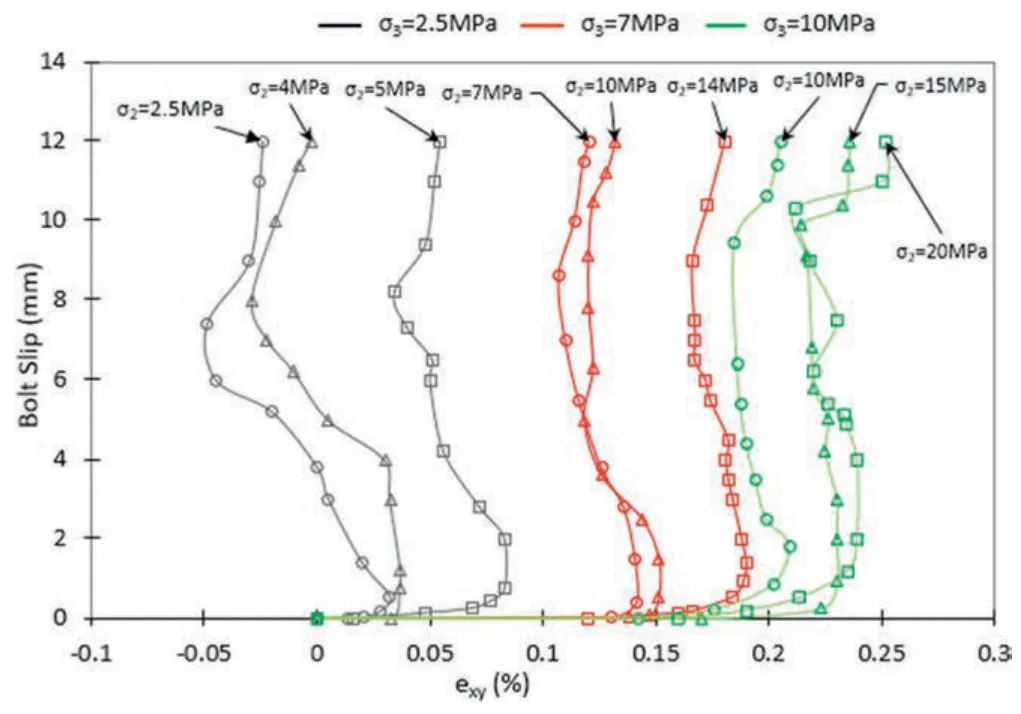
Fig.11.Relationship between the total lateral deformation (exy) and bolt slip under varying confining conditions.
(1) The results reveal that the degree of dilational deformation due to bolt displacement is significantly higher in lower confining stresses.In most cases,exydecreases with bolt slip and eventually reaches a point between the starting and minimum values.However,for specimens subjected to σ2=15 MPa,σ3=10 MPa and σ2=20 MPa,σ3=10 MPa,the contraction at the end of the tests is higher than the contraction degree at the beginning of the tests.This is believed to be due to the wider crush zone at the bolt-grout interface under higher confining stresses.
(2) In lower levels of confinement,the overall deformation of the specimen changes from contraction to dilatation,whereas in higher levels of confinement,the lateral deformation remains in a contraction state despite the occurrence of dilation to some extent in all cases.
(3) The maximum induced dilational deformation occurs when the bolt displacement reaches 7-10 mm,but this point tends to shift to the right with an increase in confining stresses.
3.4.Failure mechanism
The dominant failure mode in rock bolting systems is identified as the failure of the bolt-grout interface.This failure can occur in three main modes: dilational slip,grout sheared-off,grout shearcrushed,or a combination of these modes (Zhang et al.,2020).Previous studies have confirmed that the surface configuration of the bolt,mechanical properties of the grout,geo-mechanical properties of the surrounding rock mass,and level of confining stress define the failure mode at the bolt-grout interface(Cao et al.,2014;Cui et al.,2020;Zhang et al.,2020).According to the results of this research,the failure mode is intrinsically dependent on the confining stress conditions.Different failure patterns in the grout and surrounding artificial rock were recognized depending on the magnitudes of σ2,σ3,and the subjected push load.The confining stress applied to the outer surface of the cubic specimens resists dilation of the system,whereas the internal stress induced by bolt slip and distributed on the bolt-grout interface causes dilational deformation that may lead to radial fractures.The slip of the bolt may lever the fractures apart,causing the grout to react as a series of independent wedges (Hyett et al.,1995).The radial fractures occur where the tensile tangential stress exceeds the tensile strength of the grout and may expand to the surrounding rock.As shown in Fig.9,where there is zero confinement stress,fractures in the grout and the bottom side of the specimen are fully developed and open,whereas partially and tightly closed fractures are visible on the other sides of the specimen.As the tensile tangential stress is attenuated by the distancing from the bolt-grout interface,it is highly unlikely that fractures occur in the surrounding rock but not in the grout annulus.In cases where the failure mechanism is pure dilational splitting,the surrounding medium is yielded by the slip of the bolt,and the induced inner stress can be exerted due to the expansion of the yielded medium.Fig.7 illustrates that the shear stress generated along the encapsulation length results from the strain difference between two points on the bolt.In the absence of confining stress,the interlocking between the grout and bolt is the only factor that resists bolt slip,resulting in more uniform induced shear stress along the grouted length and minimum shear stress concentration,leading to dilation of the system instead of shearing the grout.However,as the confining stresses increase,more normal load acts on the bolt-grout interface,causing the induced shear stress near the loading point to become the highest,surpassing the shear strength of the grout.This leads to cutting of the grout asperities instead of creating dilational cracks in the grout and/or surrounding rock.Further loading extends the shear-off phenomenon to the free end section.
Photographs taken immediately after the experiments were carefully analyzed to investigate the potential relationship between testing parameters and failure patterns of the bolting systems.Fig.12 presents images obtained from the crack detection analysis.During testing,the confining stresses σ2and σ3were applied on theXandYdirections,respectively.In Fig.12a,where the external confining stresses in both directions are 2.5 MPa,radial fractures are visible in both the grout and rock,indicating that the system tends to fail under splitting.In the grout,fractures are distributed randomly,while in the rock,fractures propagate in the direction of principal stresses σ2and σ3.When the level of confining stress increases to σ2=σ3=10 MPa(Fig.12d),fractures occur mostly in the grout but with lower density compared to Fig.12a.In cases where the confining stress condition is not hydrostatic,the fracture mechanism is slightly different.The specimen shown in Fig.12b had σ2and σ3set to 10 MPa and 7 MPa,respectively.Radial fractures grew in various directions of the grout,while in the rock,fractures were initiated only in theXdirection.This may be due to the fact that 7 MPa stress subjected in theYdirection could not provide enough confinement to prevent dilation of the rock,allowing tensile tangential stress to overcome its mechanical strength.The failure mode of the specimen shown in Fig.12e,where σ2=15 MPa and σ3=10 MPa,is very similar to that of the case shown in Fig.12b,except that the fractures in the grout are largely in theXdirection.This may be associated with an increase in the magnitude of σ2to 15 MPa,which limits the weak planes to theXdirection.As the principal confining stresses reach 10 MPa and 20 MPa (Fig.12f),cracks vanish in the surrounding materials.It was noticed that there is a single visible fracture in the artificial rock depicted in Fig.12d and f,which was likely created by induced tangential stress at the grout-rock interface due to slight movement of the grout cylinder during testing.There might be micro-cracks in all cases;however,observation and image processing were not capable of detecting them.In high-stress confining conditions,Fig.12f,only a few partial and tightly closed cracks developed in the grout,but this is unlikely to have contributed to the bolt failure.The edges of the specimen shown in Fig.12e also got chipped,which could be due to higher stress concentration.

Fig.12.Initiated and propagated fractures on specimens under various confinement conditions:(a)σ2=σ3=2.5 MPa;(b)σ2=10 MPa,σ3=7 MPa;(c)σ2=14 MPa,σ3=7 MPa;(d)σ2=σ3=10 MPa;(e) σ2=15 MPa,σ3=10 MPa;and (f) σ2=20 MPa,σ3=10 MPa.
Direct observation of the bolt-grout interface after tests revealed that confinement conditions were a key factor dominating the interfacial failure modes.Fig.13 illustrates the typical failure modes at the bolt-grout interface captured at the end of the push-out tests with different confining conditions.The results were analyzed by considering the type and severity of damage that occurred to the grout asperities.The failure mechanism of systems under push testing changes from pure splitting under zero confinement(Figs.9 and 13a) to states where failure is a combination of splitting and shear-off,and the role of shear-off failure becomes more prominent when reaching higher levels of confinement.If the confining stress rises further,the failure mode of the system converts to shear-off and shear-crushed modes.From Fig.13a,it can be observed that the interface damage in zero confining stress condition is minor,due to the fact that the failure mode of the bolt-grout interface was dilational slip failure and the specimen split radially.Thus,the grout asperities remained mostly intact and undamaged.Fig.13b displays a combination of dilational failure and partially shear-off failure that occurred in the test where σ2=σ3=2.5 MPa.In this case,the dilation of the specimen was not big enough to allow the ribs to completely slide over the grout asperities.Likewise,the confining force was also not large enough to make ribs completely cut off the grout asperities.Thus,grout asperities were compressed,flattened,and cut off concurrently to some extent.This interface failure mode was observed in cases A-D.When the confining stress increased to σ2=10 MPa and σ3=10 MPa,there was purportedly enough force to avoid ribs overriding.Thus,continuous push force led to a clean cut off the grout asperities(Fig.13c).In this case,there are no signs of asperities left at the interface.With further increase in the confining stress to σ2=20 MPa and σ3=10 MPa,the damage became even deeper.In addition to the grout asperities,a layer of the grout was crushed,indicating a shear-crush failure mode(Fig.13d).A noticeable degree of smashing was also observed in the vicinity of the rock bolt in cases D-F(refer to Table 3),similar to the statement shown in Fig.13d,demonstrating a robust presence of shear-off and shear-crushed failure modes.

Fig.13.Failure modes at the bolt-grout interface under different confining stresses:(a)Unconfined(σ2=σ3=0 MPa);(b)σ2=σ3=2.5 MPa;(c)σ2=10 MPa,σ3=10 MPa;and(d)σ2=20 MPa,σ3=10 MPa.
3.5.Limitation of this study
The result of this study indicates that the non-uniform confining stresses significantly affect the axial behavior of fully grouted rock bolts.However,some limitations in practice shall still be noted and studied further.Observations revealed that specimens were partially sensitive to confining load changes resulting in difficulties in analyzing the data.This could be because of the size of specimens which were small due to the limitation of the testing equipment.Nevertheless,the properties of the materials used in the study were representative of the common engineering materials.In addition,the effects of sample size,sample strength and encapsulation length on the rock and rock bolt behaviors have been reported in previous research studies.Accordingly,it is recommended to carry out further research utilizing different arrangements including encapsulation length,specimen size,surrounding media and grout strength and other confining stress regimes.Additionally,while the push-out test has been widely utilized as an effective method for examining the axial behavior of rock bolts,it is advisable to perform a pull-out test under triaxial conditions.
4.Conclusions
Rock bolts installed in underground excavations are typically exposed to complex confining loads in which the magnitudes of the principal stresses may vary.In this study,a true triaxial testing system was utilized to investigate the response of rock bolting systems to various biaxial confining conditions.The following conclusions are drawn from this investigation:
(1) The ultimate bearing capacity of grouted rock bolts depends on the confining stresses.Increasing the principal stresses to 2.5 MPa in bothXandYdirections does not significantly enhance the bearing capacity.In this case,the increase in bearing capacity is only 3.5% compared to that with σ2=σ3=0.However,when the principal stresses are raised to σ2=σ3=10 MPa and σ2=20 MPa and σ3=10 MPa,a 38.7% and 66.6% increase in the peak load,respectively,is observed.
(2) The load-displacement curves indicate that the confinement condition has a significant effect on the behavior of system.A nearly linear relationship between load and displacement for the unconfined specimen was observed,while at lower levels of confinement,the load increased first linearly and then exponentially with displacement.In cases where the confining stresses increased to σ2=15 MPa,σ3=10 MPa and σ2=20 MPa,σ3=10 MPa,the load-slip curve became nonlinear from the start of the test.Considering the interfacial stiffness at the bolt-grout interface,stiffness decreased slightly until a displacement of 0.5 mm and then gradually decreased until failure occurred.In contrast,the initial stiffness of the confined specimens was dependent on the level of confining stress,but regardless of the confining level,it tended to decrease exponentially until failure occurred.
(3) A linear relationship can be observed between σ2andregardless of the rate ofk.It was also noted that at a certain level of σ3,the effect of σ2on τigradually decreases.It is anticipated that at a particular level of σ2,may not increase any further.It is also revealed that the effects of principal stress ratio onare more significant at higher values of σ3.
(4) The relative lateral deformation curves of the specimens indicate that,for all cases,there are three discrete stages.The first stage involves shrinkage when confining stress is applied to the specimen,followed by a dilational stage when the bolt moves.The dilation rate decreases as the bolt slip reaches around 7 mm of displacement.After this point,the specimens tend to shrink again until the end of the test.The magnitude of confining stress dominates the shrinkage and dilational behavior.
(5) It was observed that at lower confinements,specimens tended to fail via splitting,while at higher loads,the failure mechanism changes to pure interfacial shear-off and shearcrushed.Radial fractures propagated in both the annulus area and artificial rock.However,in cases with medium levels of confinement,fractures only appeared in the grout zone.At higher levels of confining stress,no visible fracturing occurred.
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgments
This work was financially supported by the School of Engineering,the University of Southern Queensland.The in-kind support from Minova Australia,in particular Mr.Robert Hawker,is greatly acknowledged.
 Journal of Rock Mechanics and Geotechnical Engineering2024年3期
Journal of Rock Mechanics and Geotechnical Engineering2024年3期
- Journal of Rock Mechanics and Geotechnical Engineering的其它文章
- Limit load and failure mechanisms of a vertical Hoek-Brown rock slope
- Limit state analysis of rigid retaining structures against seismically induced passive failure in heterogeneous soils
- Bearing capacity of circular footings on multi-layered sand-waste tire shreds reinforced with geogrids
- Experimental investigation on the permeability of gap-graded soil due to horizontal suffusion considering boundary effect
- Damage constitutive model of lunar soil simulant geopolymer under impact loading
- Wetting-drying effect on the strength and microstructure of cementphosphogypsum stabilized soils
