售电侧开放市场环境下基于多分位鲁棒极限学习机的短期负荷预测技术

杨希 王刚 张鹏宇 李颖 张国锋

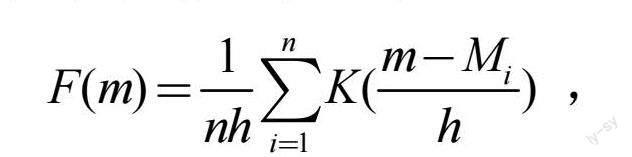
摘  要：该文基于极限学习机算法设计一种用于短期负荷预测的多分位鲁棒极限学习机模型，该模型能解决传统预测模型抗干扰能力差的缺陷，可以在面临不确定性因素干扰的情况下准确预测负荷。对传统模型和多分位鲁棒极限学习机模型的鲁棒性和多分位性进行验证，对比结果表明，多分位鲁棒极限学习机模型的鲁棒性更好，在不同分位下的预测精度更高。

关键词：多分位鲁棒极限学习机；短期负荷预测；核概率密度函数；输入量；预测结果

中图分类号：TM743 文献标志码：A          文章编号：2095-2945（2024）08-0094-04

Abstract： In this paper， a multi-quantile robust extreme learning machine model for short-term load forecasting is designed based on the extreme learning machine algorithm. This model can solve the defect of poor anti-interference ability of the traditional forecasting model. The load can be predicted accurately in the face of uncertain factors. The robustness and multi-quantile of the traditional model and the multi-quantile robust limit learning machine model are verified. The comparison results show that the multi-quantile robust limit learning machine model has better robustness and higher prediction accuracy under different quantiles.

Keywords： multi-quantile robust limit learning machine; short-term load forecasting; kernel probability density function; input; prediction results

在售電侧开放市场环境下，电力负荷开始作为一种特殊商品进入电力市场，这种情况下电力用户能根据电价的波动变化，选择在电价较低时用电，从而降低了用电成本。对于供电公司来说，由于用户用电行为具有随机性，基于维护电网运行稳定等方面的考虑，准确进行负荷预测显得尤为重要。供电公司在售电侧开放市场环境下，设计一种响应更加迅速、预测更加准确的短期负荷预测模型，成为现阶段的重要研究课题。

1  多分位鲁棒极限学习机的模型构建

1.1  极限学习机算法

极限学习机（ELM）是一种单隐含层前向神经网络机器学习算法，由输入层、隐含层和输出层3部分构成，组成结构如图1所示。

图1中，输入层的每个节点代表了一个输入变量，输出层的节点数量不一。当输出节点为1时，为单步输出；当输出节点有2个及以上时，为多步输出。隐含层的节点与输入层节点之间的权值为ω，隐含层节点与输出层节点之间的权值为β。极限学习机的数学模型可表述：假设用于负荷预测的数据样本集合为

S={（xi，ti）} xi∈Rm，i=1，2，3，…，N。

在单隐含层前向神经网络中，含有N个隐含层节点，其数学模型可表示为

式中：xi表示影响负荷预测的所有变量，以集合形式表示xi=[xi1，xi2，…xin]，yi表示在i时刻的负荷值，bi表示该神经网络中第i个隐含层节点的偏置，βi和ωi表示第i个节点对应的权值，g（）表示激活函数。将样本数据输入到该数学模型中进行多次迭代后，可以求得未知权值系数的最优值，此时模型的训练误差最小，可用于负荷预测[1]。

1.2  多分位鲁棒极限学习机模型的确定

以ELM算法为基础建立的鲁棒极限学习机（ORELM）模型在负荷预测中表现出2个优势：其一，利用调节系数进行输出权值和训练误差的权衡，使得负荷预测模型对于异常数据的鲁棒性得到了提升；其二，利用1-范数的系数特性避免了异常值带来的干扰。基于上述2项特点，使得鲁棒极限学习机模型的负荷预测结果较为精确。但是该模型在实际应用中也面临一个无法回避的问题，即售电侧新环境下负荷曲线具有随机性和变动性，而鲁棒极限学习机模型只能对某个确定点的负荷进行预测，不适合这种随机多变的场景[2]。基于此，本文在鲁棒极限学习机模型的基础上，引进“分位回归”算法建立了多分位鲁棒极限学习机模型（MQR-ORELM）。对比2种模型，有2个共性，其一是简易方程都是线性的输出矩阵方程；其二是求解的未知参数都是模型的输出参数；有1个区别，前者采用拉格朗日算法，属于非线性求解方法，后者采用内电法和平滑法等多种算法，属于线性规划求解方法。

基于上述分析，构建了多分位鲁棒极限学习机模型，其数学表达式为

Q（x|τ）=ωU+βH ，

式中：Q（x|τ）为不同分位下多分位鲁棒极限学习机模型的负荷预测值，ω表示分位回归的模型核心部分，T表示采样时间，U表示自变量矩阵，β表示参数矩阵，H表示输入变量矩阵，两者结合能够显著提高该模型的预测精度。在得到多分位鲁棒极限学习机模型后，按照与上文相同的方法，使用样本数据对该模型进行迭代求和。迭代次数不设上限，直到求解出β和ω 2个未知参数为止。迭代结束后，即可确定多分位鲁棒极限学习机模型的结构，在此基础上选择合适的分位，得到不同分位下的负荷预测结果。

1.3  多分位鲁棒极限学习机模型的验证

从应用效果来看，多分位鲁棒极限学习机模型可以在场景多变的情况下对短期负荷进行预测，同时通过选取合适分位的方式提高了预测结果的精确性，更加适合售电侧开放市场环境下的负荷预测[3]。为了深入、全面地了解多分位鲁棒极限学习机模型的性能，本文分别选择鲁棒性和多分位性两项特性展开了验证。

1.3.1  鲁棒性验证

较高的鲁棒性是保证多分位鲁棒极限学习机模型能够准确预测短期负荷的关键。本文选择带异常值的非线性随机函数进行该模型的鲁棒性验证，该函数的表达式为

式中：r1和r2是[-1，1]区间内的2个随机值。如果存在“r1=0”且“r2=0”的情况，说明该函数中无异常值。在2个随机值均不为0的情况下，选择500个数据点展开训练；对于任意一个数据点，测试的样本中x服从[-10，10]的均匀分布。除此之外，另外选择了10 000个点用于多分位鲁棒极限学习机模型的验证；对于任意一个点，验证的样本中x服从[-11，11]的均匀分布。y表示与x对应的函数输出值。为了减轻数据处理的工作量，本文只研究了异常值（k）为0、40和80时的负荷预测结果。异常值能够客观表示模型所受环境的干扰程度，异常值越大，表明干扰越激烈。选取3个典型分位（τ），分别是0.1、0.5和0.9。同时，为了更加直观地展示多分位鲁棒极限学习机模型在短期负荷预测方面的应用效果，选取了传统的鲁棒极限学习机模型作为对照，预测结果如图2—图4所示。

分别统计2种模型在异常值为0、40、80时的训练值和预测值，统计结果见表1。

结合图2—图4和表1可知，从整体上来看，2种模型对于短期负荷的预测精度都会随着异常值的增加而降低，两者的泛化性能较为接近。但是横向对比可以发现，多分位鲁棒极限学习机模型的训练误差更小，表明该模型具有更好的鲁棒性。

1.3.2  多分位性验证

多分位性可以表示模型在场景变动下对于短期负荷预测结果的准确性。在多方位性验证中，本文分别选择了二次函数、高斯函数和西格玛函数对模型进行逼近处理，并对比2种模型在3种函数下的逼近效果，由此来判断多分位鲁棒极限学习机模型中加入的多分位功能是否发挥了作用[4]。该试验中使用到的训练集合与验证集合与上文鲁棒性验证试验一致；多分位鲁棒极限学习机模型的典型分位选择上，共设有0.1、0.3、0.5、0.7和0.9五个，预测结果见表2。

由表2数据可知，2种模型在逼近3个函数时，均表现出较为理想的拟合效果。横向对比来看，多分位鲁棒极限学习机模型在5个典型分位下的预测结果，总体上要优于鲁棒极限学习机模型的预测结果。这也表明在多个分位场景下，相比于只能定点预测负荷的鲁棒极限学习机模型，本文设计的多分位鲁棒极限学习机模型在提高预测结果精度方面具有显著优势。

2  基于多分位鲁棒极限学习机的短期负荷预测

2.1  核概率密度函数的选择

通过上文的模型预测试验可知，不同分位下的预测精度会表现出一定的差异。为了确定不同分位下的最佳预测精度，本文提出了一种基于核概率密度函数的解决方案，其原理：选定（0，1）区间，从中获取多个分位值，然后利用上文求得的多分位鲁棒极限学习机模型，计算出不同分位值下对应的预测值。最后将预测值作为输入量，输入到核概率密度函数中进行计算，统计计算结果后绘制出概率分布图，从而更加直观地显示预测值信息[5]。由此可见，核概率密度函数的选择是进行短期负荷预测的关键。假设多分位鲁棒极限学习机模型在n个分位下的预测值分别为M1，M2…，Mn，则核概率密度函数可表示为

式中：F（m）表示概率密度函数的估计值，h表示窗宽，K（）表示核函数。根据上式可知，函数估值除了与核函数有关，还受到了样本数量和窗宽的影响。在确定核概率密度函数后，采取积分均方误差对其进行逼近，计算出最佳的窗宽。将其重新带入到核概率密度函数中，即可得到短期负荷预测值的概率分布图。

2.2  短期负荷预测流程

基于上述模型进行短期负荷预测，具体步骤如下。

步驟1：收集气象因素、电价数据、历史负荷数据，并对其进行归一化处理，目的是防止数据差异导致最终训练结果出现误差。归一化公式为

Bj=，

式中：bmax表示各类数据组成的数据集合在多选时间尺度内xi={b1，b2，...，bn}样本数据的最大值。

步骤2：对完成归一化处理的数据，按照历史负荷变量数据进行分解，并构建基于电价导向的需求相应模型。获取电价数据，并将其作为输入量带入到响应模型中，获得响应影响因子。将该因子作为输入量，带入到预测模型中，并对气象因素、时间因素等负荷影响因素进行处理。

步骤3：将输入量带入到本文设计的多分位鲁棒极限学习机模型中，在设定的区间范围内选择若干个合适的分位，利用模型求得各个分位下对应的预测值。

步骤4：使用核概率密度函数处理步骤3中得到的预测值，得到更为全面的预测值信息。

整个预测步骤如图5所示。

3  结束语

现阶段使用的许多短期负荷预测模型只能对某个确定点的负荷进行预测，而售电侧新市场环境中存在大量不确定因素，导致负荷预测结果的精度受到干扰。针对这一问题，本文基于分位回归算法建立了多分位极限鲁棒学习机模型，从模型试验情况来看，表现出良好的鲁棒性和多分位性能，能够有效应对短期负荷预测中不确定因素带来的干扰，保证了预测结果的高精度。

参考文献：

[1] 王增平，赵兵，贾欣，等.基于差分分解和误差补偿的短期电力负荷预测方法[J].电网技术，2021（7）：1159-1160.

[2] 刘音，孙兵，苏彪，等.基于大数据的短期负荷预测技术研究[J].信息技术，2022（12）：183-188.

[3] 乔石，王磊，张鹏超，等.基于模态分解及注意力机制长短时间网络的短期负荷预测[J].电网技术，2022（7）：161-163.

[4] 赵洋，王瀚墨，康丽，等.基于时间卷积网络的短期电力负荷预测[J].电工技术学报，2022（5）：37-38.

[5] 徐先峰，赵依，刘状壮，等.用于短期电力负荷预测的日负荷特性分类及特征集重构策略[J].电网技术，2022（4）：9-11.