复杂测量模型不确定度的数值评定

高申翔 韩 璐 霍 莹 桑志勇

(中国卫星海上测控部，江阴 214431)

0 引言

评定测量不确定度通常有GUM法和蒙特卡洛法[1]。GUM法是工程上经常使用的方法，其核心是标准偏差理论和基于多元函数全微分的不确定度传播律[2]。但是对于函数形式很复杂的测量模型，解析输入量的偏导函数很繁琐，以致于有时无法用解析的方法求解输出量的标准偏差。本文介绍的方法是：当我们知道了输出量和输入量的函数关系，也知道每个输入量的最佳估计值及其不确定度(或分布规律)时，可以考虑用数值方法计算输入量在特定点的偏导数，再计算输出量的标准偏差。

1 不确定度传播律及多元函数偏导数的数值计算

假设有测量模型如式(1)，其中Y是被测量，也叫输出量；Xi(i=1,2,…,N)为输入量。

Y=f(X1,X2,…,XN)

(1)

如果Xi相互独立，它们的标准偏差分别为σXi，则Y的标准偏差为[3]

(2)

式(2)即不确定度传播律，其中∂f/∂Xi是f关于Xi的偏导函数，也叫Xi的灵敏系数。

根据多元函数偏导数的定义[4]，对于式(1)，如果f在点P=(x1,x2,…,xN)的某一邻域内有定义，当Xi在点P处有增量Δxi，其它自变量保持不变时，Y有增量

Δyi=f(x1,x2,…,xi+Δxi,…,xN)-f(x1,x2,…,xN)

(3)

如果极限

(4)

存在，则称此极限为函数f在点P处对Xi的偏导数。

点P即为输入量的最佳估计值。如果Xi的变化很小，则Xi在点P处的偏导数近似为

(5)

增量Δxi的确定方法是：根据所掌握的Xi的分布信息，估算其分布区间半宽度[5]，将Xi的分布区间半宽度作为Δxi。具体有以下几种情况：

1)已知Xi的扩展不确定度U，则Δxi=U；

2)已知Xi的误差限为±a，则Δxi=a；

3)已知Xi的标准偏差s和概率分布，则Δxi=kp·s；kp是与Xi的分布形式和置信概率有关的包含因子。如果不知道Xi的分布，则假定它服从均匀分布(矩形分布)[3]。

2 测量不确定度的数值评定

下面用一个实例介绍测量不确定度的数值评定方法。

在无线电校准中，用交替比较法校准微波功率敏感器时，如果我们考虑失配对测量结果的影响，则被校准功率敏感器的校准因子为[6]

(6)

式中，输入量Kbs，Pbu和Pbs为标量；ΓG，Γu和Γs为矢量；将式(6)化为标量形式

(7)

首先介绍式(7)中各量的物理意义及相关数据，如表1所示。

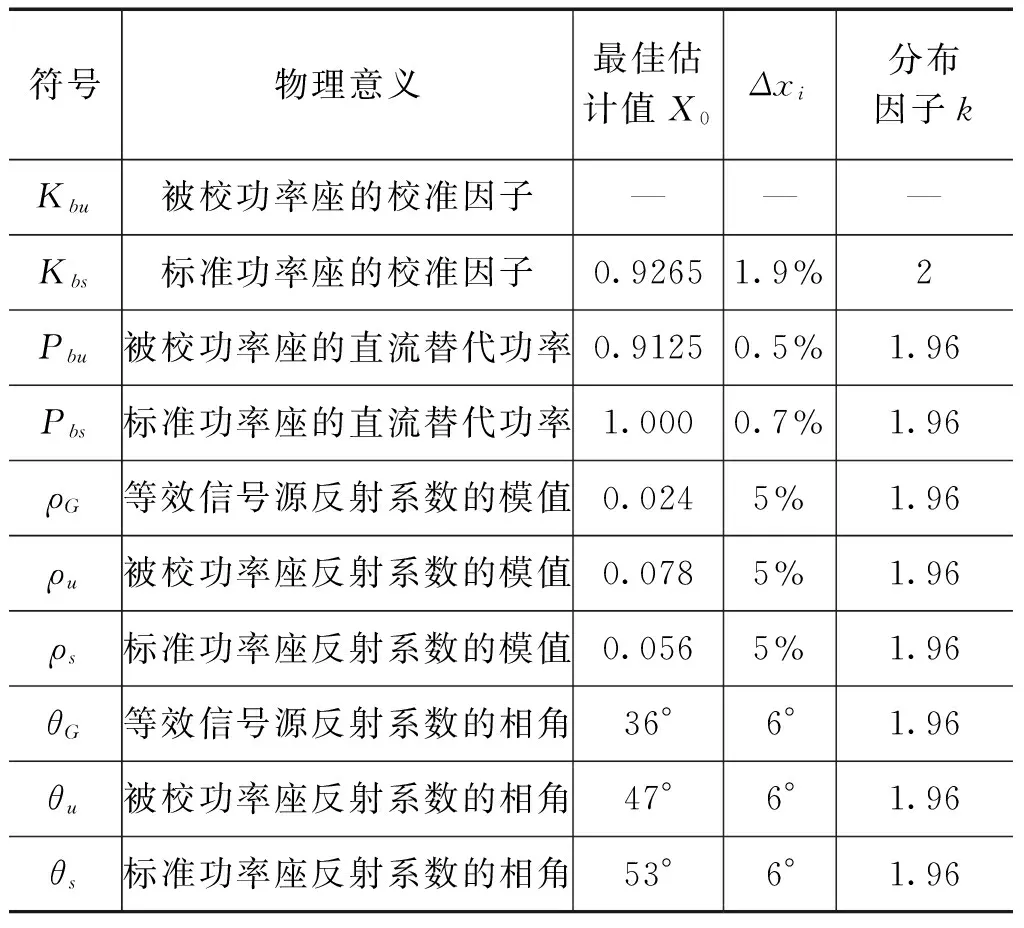
表1 式(7)中各量的物理意义及相关数值

评定过程如下：

1)将各输入量的最佳估计值代入式(7)计算Kbu的最佳估计值。

2)根据有关信息(校准证书、测量仪器说明书或重复测量数据等)确定各输入量的最大变化量Δxi。

对于本例，标准功率座校准因子的最大变化量为其校准值的扩展不确定度U；直流替代功率的最大变化量为功率计的测量误差限；反射系数模值和相角的最大变化量为矢量网络分析仪的测量误差限。

3)根据式(5)计算每个输入量在最佳估计点的偏导数。

4)用A类或B类方法评定各输入量的标准不确定度[3]。

5)根据式(2)计算输出量Kbu的标准不确定度。

6)计算输出量Kbu的扩展不确定度。因为输入量众多且每个输入量的影响都比较小，可以认为输出量服从正态分布[7]。如果取置信概率为95%，则Kbu的扩展不确定度为

U=1.96·σ(Kbu)

(8)

3 计算工具

从评定过程可以看出，该方法的计算量是很大的，实践中可以针对每个测量模型编制计算工具。笔者针对式(7)用Excel编制了电子计算表格，只要输入各输入量的最佳估计值和不确定度信息，就可以立即得到输出量的扩展不确定度。限于篇幅，这里不详细介绍。

4 对计算误差的评估

不确定度传播律是对多元函数泰勒公式的一阶近似[2]，基于式(5)的偏导数数值计算也存在误差，因此式(8)存在方法误差。通常用蒙特卡洛法验证不确定度传播律的评定结果[8-9]。本文以蒙特卡洛法的试验结果为参照，针对式(7)做了方法比对试验，试验结果如表2所示。对灵敏系数较大的Pbs做了方法误差与输入量变化量的相关性试验，试验结果如表3所示。

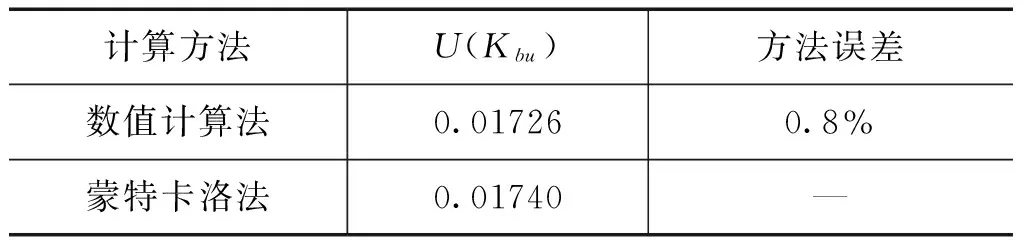
表2 计算方法的比对试验

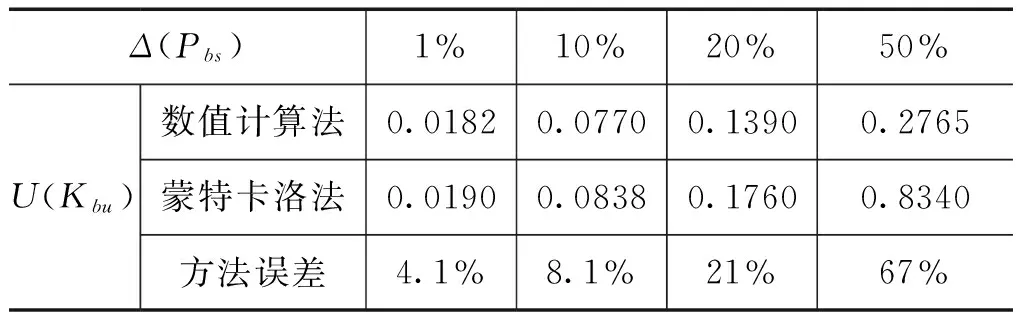
表3 计算误差与输入量变化量的比对试验

从表2可以看出，当输入量的变化量较小时(具体数值见表1)，数值计算法相对于蒙特卡洛法的计算误差不到1%。由表3进一步看出，计算误差随着输入量变化量的增大而增大，当变化量不超过20%时，计算误差都是可以接受的。

5 结束语

本文通过无线电计量领域的一个实例介绍了复杂测量模型不确定度的数值评定方法，通过与蒙特卡洛试验结果的比较评估了该方法的计算误差。试验结果表明，当输入量的变化量不超过20%时，该方法的计算误差一般不超过25%。与偏导数的解析计算法比较，该方法省却了繁琐的导函数推演；与蒙特卡洛法比较，该方法只要编辑公式，不需要写程序代码，而且计算时间比蒙特卡洛法少得多。

[1] 国家质量技术监督局.JJF 1059.2—1999 用蒙特卡洛法评定测量不确定度[S].北京：中国计量出版社，2010

[2] 叶德培.测量不确定度[M].北京：国防工业出版社，1996：22

[3] 国家质量技术监督局.JJF 1059.1—1999 测量不确定度评定与表示[S].北京：中国计量出版社，2000

[4] 同济大学数学教研室.高等数学(下册)[M].第三版.北京：高等教育出版社，1989

[5] 李庆忠，李春燕.合成不确定度的两种评估方法[J].计量技术，2007(6)：57-59

[6] 冯新善，等.高频、微波功率的计量测试[M].北京：中国计量出版社，1985：123-125

[7] 盛骤，等.概率论与数理统计[M].北京：高等教育出版社，1990：134

[8] 高申翔，石明华，韩璐 等.失配误差的计算机辅助分析与评定 [J].计量技术，2012(10)：19-21

[9] 崔孝海，曲璐.蒙特卡罗方法在微波功率测量不确定度分析中的应用[J].计量学报，2008(1)：77-79