支撑共振法测量固体材料杨氏模量
韩立立 王 岍 苗笛声
(中国石油大学(华东)理学院,青岛 266580)
0 引言
弹性材料承受正向应力时会产生正向应变,在形变量没有超过对应材料的一定弹性限度时,定义正向应力与正向应变的比值为这种材料的杨氏模量。
杨氏模量是选定机械零件材料的依据之一,是工程技术设计中常用的参数。杨氏模量是物体间原子、离子或分子之间键合强度的反映,其值越大,使材料发生一定弹性变形的应力也越大,即材料刚度越大[1]。杨氏模量的测定对研究金属、光纤、半导体、纳米、聚合物、陶瓷、橡胶等各种材料的力学性质有着重要意义。
测量杨氏模量的方法一般有拉伸法、梁弯曲法、振动法、内耗法等,还出现了利用光纤位移传感器、莫尔条纹、电涡流传感器和波动传递(微波或超声波)等实验技术和方法测量杨氏模量。本文研究采用的是支撑共振法测材料杨氏模量。
1 实验仪器及基本原理
功率函数信号发生器可产生多种波形,输出频率范围5Hz~500kHz。激振器将声频信号转换为机械振动信号,振动信号通过试样棒传到拾振器上转变为电信号,电信号进入示波器中显示。试样棒直接搭放在两个换能器上,无需进行其他处理。
信号发生器通过激振器使试样棒做弯曲振动,满足动力学方程[2]:
(1)
该长棒的轴线沿x方向,式中y为棒上距左端在x处截面的y方向上的位移;E为该棒的杨氏模量;ρ为材料密度;S为棒的横截面积;J为棒的某一截面的惯性矩;t为时间。
用分离变量法解方程得:
(2)
式中:m为棒的质量;d为直径;L为试样棒的长度;f为基频振动的固有频率。
式(2)只有在试样的直径与长度之比d/L趋于零时才能满足,但实际测量时,由于不满足d< (3) 表1 径长比与修正系数的对应关系 实验测量当中,激发换能器、接受换能器、支架等部件都有自己的共振频率,可能以其本身的基频或高次谐波频率发生共振。同时,试样本身也会有多个共振峰,因此会在实验中测到多组共振信号,必须采用一定方法判断示波器上显示的信号是否为试样棒的共振频率。 判断方法如下:先通过理论计算,估算基频共振频率数值,真正的基频共振频率在估算频率附近。实验样品中玻璃的杨氏模量理论值为71.68GPa,根据式(3)得:玻璃棒基频共振频率为730.5939Hz。 根据方程(1)的解知,试样在作基频振动时存在两个节点,它们的位置分别距端面0.224L和0.776L。这两点的振动频率即为基频振动频率。将试样支撑在这两个位置时振幅几乎为0,试样棒难以被激振。故测量这两个点周围点的振动频率,再用外延法找到节点处的振动频率。实验测得玻璃棒共振频率如表2所示。用电脑软件进行数据拟合[3],得到图像,如图1所示。 表2 实验测得玻璃棒共振频率 图1 玻璃棒数据拟合图像 由拟合所得图像知:玻璃棒在0.224L处共振频率约为735.5Hz。将频率升高到所判定的基频2.74倍处,发现玻璃棒在2000Hz附近,存在共振,即一次谐波共振,证明735Hz为真正的基频共振频率。根据式(3)计算,得到玻璃棒杨氏模量E1=73.54GPa。结果接近真实值71.68GPa。相对误差2.6%。 测量仪器会引起部分测量误差,甚至导致部分材料无法测得。根据测量实际情况,总结出所测试样棒需要满足以下几点要求: 1)试样棒要长短适中,本实验装置中换能器距离最大21.00cm,最小可以达到4.50cm,要测量0.224L附近的共振频率,则试样棒的极限长度范围为8.2~38.5cm。但使用外延法时,欲使测量结果更准确,则试样棒最佳长度为15~30cm。极限长度范围的计算方法:换能器最小距离/0.552为试样棒最短长度;换能器最大间距/0.552为试样棒最大长度。 2)真实共振频率应与仪器共振频率有较远差距,本实验仪器DCY-系列共振频率约为110Hz。由于仪器共振峰有一定宽度,若所测试样棒真实共振频率过于接近110Hz,则会受到仪器共振频率干扰,导致测量错误。因此本实验中真实共振频率要在150Hz以上。在实验之前必须搞清仪器共振频率,实验中必须避开这一频率进行数据测量。 3)试样棒不能弯曲,若试样棒弯曲,则无法得到正确的测量频率,并且试样棒必须是脆性材料,这是共振法测量杨氏模量的局限,对于非脆性材料(如橡胶棒),利用这种方法无法测得共振频率。对于非脆性材料,可利用强迫振动方法测得其杨氏模量[4]。 共振法测量固体材料杨氏模量结果稳定,理论同实验吻合度好,适用于各种金属及非金属(脆性) 材料的测量,也可用于高温下测量[5]。在测量过程中,找出基频对称型共振状态是动态法测量杨氏模量的技术关键,这包含两个问题:判断试样是否处于共振状态与判别所出现的共振信号是否属于对称型基频下的共振信号。 本实验通过对数据结果的分析研究,找到了测量非金属样品杨氏模量的一般方法,同时研究了基频共振的判断过程,此法可以用于多种材料的测量和鉴频。本实验还证明了对于较长试样棒,依然可以利用外延法,借助软件拟合,得到较准确的基频共振频率。 [1] 杨周琴.共振法测量金属材料的杨氏模量实验探讨[J].新课程,2011(9):64-65 [2] 李艳琴,赵红艳,李学慧,胡瑞.动力学共振法测量固体杨氏模量[D].大连:大连大学物理科学与技术学院,2009 [3] 万志龙.Origin在动态法测量杨氏模量实验中的应用[J].技术物理教学,2009(2):33 [4] 贺西平.强迫振动方法确定粘弹性细棒的复杨氏模量[J].声学学报,2012(2):193-197 [5] 周晓明.三种杨氏模量测量方法比较[J].实验科学与技术,2011(6):97-99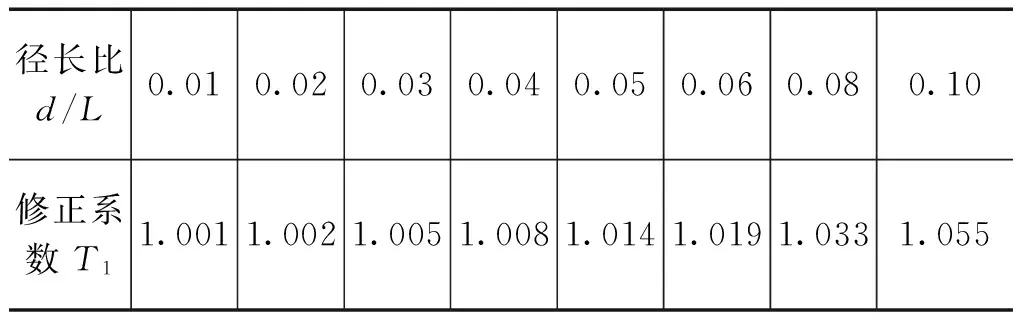
2 实验数据处理
2.1 基频共振的判断
2.2 外延法数据拟合


3 实验结论及证明
4 实验分析
5 结束语

