某不稳定滑坡对邻近居民点涌浪影响研究

杨猛 拾亭

摘  要：水库滑坡涌浪会对邻近居民的生命财产安全产生重大影响，但实际工程中涌浪的计算方法却十分复杂。该文以某滑坡为研究对象，通过分析其地质条件及滑坡基本特征，对滑坡的整体稳定性进行定性评价，采用潘家铮法和中国水科院经验公式法对滑坡涌浪高度进行估算。计算结果表明，研究发现在“暴雨工况+蓄水”825 m下，居民点涌浪高度为3.52 m，应采取相应的防浪措施。该文对类似滑坡灾害影响分析具有一定参考价值。

关键词：滑坡；稳定性；涌浪计算；潘家铮法；防浪措施

中图分类号：TV139.2+3     文献标志码：A          文章编号：2095-2945（2024）08-0071-05

Abstract： The landslide surge of the reservoir will have a great impact on the life and property safety of the nearby residents， but the calculation method of the surge in the actual project is very complicated. In this paper， taking a landslide as the research object， through the analysis of its geological conditions and the basic characteristics of the landslide， the overall stability of the landslide is qualitatively evaluated， and the surge height of the landslide is estimated by the Pan Jiazheng method and the empirical formula method of the Chinese Academy of Water Sciences. The calculation results show that under the "rainstorm condition + water storage "of 825 meters， the surge height of the residential area is 3.52 meters， and the corresponding wave prevention measures should be taken. This paper has a certain reference value for the impact analysis of similar landslide disasters.

Keywords： landslide; stability; surge calculation; Pan Jiazheng method; wave prevention measures

在山體坡面或陡坡上的滑坡过程中，由于土石的滑落及撕裂作用，产生大量涌浪会给周围环境和人类活动带来严重的危害，直接威胁人类生命安全并毁坏建筑物和基础设施，因此对滑坡涌浪的研究十分必要[1]。

近年来，许多专家学者对滑坡涌浪的影响进行了深入研究。薛宏程等[2]在等效流体假设的基础上，用定制的函数来编写滑坡体沿滑动面运动的摩擦阻力程序，使用 Realizablek-ε紊流模型与 VOF法，构建出了碎石土滑坡涌浪数值模拟模型，其计算得到的涌浪波幅具有较高的准确性。王佳佳等[3]通过构建缩放后的矩形水槽滑坡涌浪三维物理实验，研究滑坡体积、流速、水深等因素对堆积体形貌、涌浪特性的影响，揭示滑坡与水之间的能量转换机制。马斌等[4]基于量纲分析的非线性回归方法，建立了坝肩处浪高的预报公式。薛宏程等[5]在对水库滑坡涌浪进行三维数值仿真的基础上，对水库在不同时间点上的涌浪进行了定量分析。李东阳等[6]提出了一种基于扩展离散元（DEM）和计算流体力学（CFD）的数值模拟方法，并将流体容积法（VOF）引入到局域平均 DEM-CFD耦合方法中，构建一种适用于河床自由表面演变的扩展 DEM-CFD耦合数值模拟体系，以跟踪滑坡涌浪的生成和传播过程。郑飞东等[7]通过水槽物理模型实验，对滑坡消散过程对涌浪波形特征的影响进行了初步探讨，发现随着滑坡体分散指数的增加，初始涌浪的最大幅度、最大波高降低。王梅力等[8]以物理模型试验观测数据为基础，对初始涌浪的最大波高、最大周期、有效波高、有效周期及波陡特征值进行了统计和计算，运用无量纲及多元回归分析方法，最终得出了首浪高度的计算公式。徐卫亚等[9]将斜条分法、水阻力等传统滑动速度分析方法相结合，建立了一套适合于复杂分汊河段涌浪远场传播的计算方法。

本文以某滑坡为研究对象，通过分析滑坡的整体稳定性，采用了潘家铮法和水科院经验公式法对滑坡在邻近居民点的涌浪高度进行估算，并对计算结果进行分析，本文对类似滑坡灾害研究具有一定参考意义。

1  工程概况

金沙江白鹤滩水电站位于金沙江中下游（攀枝花-宜宾），为大型水电站，其坝型是一座混凝土双曲拱坝，正常蓄水位825 m，死水位为765 m。象鼻岭居民点场地原始地面高程800～827 m，垫高造地后进行移民安置居民点建设，垫高后场地高程827.3～828.7 m，规划围地总面积约140亩（1亩约等于667 m2），规划安置人口约1 618人。

王家山滑坡位于小江右岸王家山北侧，距离象鼻岭居民点直线距离约1.3 km，如图1所示。白鹤滩水电站水库蓄水后，该滑坡在特定工况下发生失稳将会产生涌浪，影响周边居民的生命和财产安全。因此，对该滑坡涌浪进行研究极其重要。

2  滑坡区地质条件

白鹤滩水电站水库区小江支库王家山段，左岸为格勒坪子（象鼻岭），右岸为王家山岸坡，坡面地形较凌乱，冲沟较发育，从南往北主要发育2条小冲沟，沟内多季节性流水，雨季流量较大。该段岸坡地层岩性复杂，将地层由老到新分述见表1。

岸边地下水以孔隙水和基岩裂隙水为主，孔隙水埋藏深度一般不大，主要赋存于小江冲洪积层内，且受地表降雨和沟谷水的补给。基岩裂缝水主要存在于斜坡上的裂缝中，并以大气降雨为主要补给来源。白鹤滩水电站水库蓄水后，受库水位影响，该处地下水位会有所抬升。

3  滑坡特征与稳定性分析

3.1  基本特征

王家山滑坡位于小江右岸北侧，左右侧分别发育1#及2#冲沟，2条冲沟在滑坡体后部相交，具有“双沟同源”“圈椅状”的特点，滑坡体上植被稀疏，主要以灌木、杂草为主，如图2所示。

从地貌上看，滑坡后缘特征明显，有“双沟同源”“圈椅状”的特点；滑坡左侧以1#冲沟为界，该冲沟约呈S62°W流向，基岩裸露，岩体破碎；滑坡右侧以2#冲沟为界，该冲沟约呈N75°W流向，冲沟左岸地形坡度15～35°；滑坡前缘至小江边，该处地形较陡，小规模滑塌现象明显，受其影响，剪出口不明显。

3.2  稳定性分析

王家山滑坡所在岸坡地形较陡，为第四系崩坡积物所覆盖，厚度较大，且距离小江断裂较近，坡体在自重作用下，在暴雨或地震条件下，沿基岩和覆盖层边界发生破坏，滑坡体积约611万m3。

现场调查发现，滑坡前缘存在塌滑破坏现象，位于滑坡体中央的S303省道（2016年扩建）的路面、挡墙、护坡出现隆起、开裂现象，路面出现塌陷、开裂等变形征兆，开裂宽度在20～30 cm，沉降深度在40～50 cm。

以上种种迹象均表明滑坡现状虽整体处于基本稳定状态，但在暴雨工况下，滑坡整体处于欠稳定状态。当蓄水高程超过825 m后，滑坡前缘会被库水所淹没，坡体内骨架间细颗粒物质会受到浸泡，土体物理力学参数将有所降低，滑坡稳定性下降，有发生整体滑动破坏的可能。

4  涌浪估算

4.1  最大入水速度估算

4.1.1  潘家铮法

潘家铮法根据动力平衡条件，求每滑动微小水平距离△L后的速度。其中水平速度计算公式为

vx=， （1）

式中：v0为滑体的初始速度；ax为滑体的水平加速度，可通过滑体的动力平衡条件得到；△L为各条块的宽度。

根据潘家铮法计算出滑坡整体失稳破坏的最大速度为7.44 m/s。

4.1.2  美国土木工程师协会推荐公式法

美国土木工程师协会推荐的计算方法是，将滑板置于半无限大的水中，视为一个整体，并将其重心作为一个质点进行移动，计算出滑板的滑动速度，滑板滑动的动力为下滑力与抗滑力之间的差值，由此计算出滑板滑动S距离后的滑速vs为

式中：？琢为滑动表面的倾斜角度；W为滑体单宽重量；φ和c为滑动面剪切强度的参量；H为重心到水面的高度；l为滑坡体与滑面接触面长；g为重力加速度，9.8 N/kg。

根据美国土木工程师协会推荐公式法计算得出滑坡最大速度为13.22 m/s。

4.1.3  谢德格尔法

谢德格尔法考虑了滑坡体的体变效应，研究表明，滑坡体的体变与滑坡体的当量摩擦系数（fe）在对数坐标系下是线性的。二者之间的关系公式为

lg fe=algV+b， （3）

式中：V为滑坡体体积；a＝-0.156 66；b＝0.622 19。据V求出fe后，按下式计算滑速

lg fe=algV+b，（4）

Vs=。（5）

计算得出滑坡整体失稳的最大速度为16.81 m/s。

4.2  涌浪高度估算

4.2.1  潘家铮法

潘家铮给出了一种计算模型，该模型中考虑了坡度对波面反射的影响，在坡度发生水平形变时，所引起的初浪高度可由下述公式表达

ζ0=1.17（ν/）h。 （6）

当岸坡上厚度为？姿的滑坡体以速度ν′进入水库后，初始浪的高度ζ0为

ζ0=f（ν′/）h， （7）

式中：f（ν′/）的变化视ν′/的大小而定，特别地，当0＜ν′/＜0.5時，f（ν′/）≈ν′/；当0.5＜ν′/＜2时，f（ν′/）呈曲线变化；当ν′/＞2时，f（ν′/）≈1。

对岸距滑坡中心区距离为x的A点最高涌浪由下式给出

，（8）

式中：n取1、3、5…；？兹n为传到A点的第n次入射线岸坡法线的交角；B为河道宽度；L为滑体宽度；k为波的反射系数，取0.9～1.0；x0为滑坡区中心到A点的水平距离。

根据潘家铮法，计算得到了该滑坡的最大入水流速为7.13 m/s，并推算出该滑坡发生在象鼻岭居住区附近时涌浪高为3.52 m。

4.2.2  中国水科院经验公式法

中国水利水电科学研究院考虑水库滑坡的滑速和滑体的体积因素，并建立了三者间如下的关系，入水点最大涌浪高度计算公式如下

hmax=k■V0.5 ， （9）

式中：k取0.12；V为滑坡体积，万m3；u为滑速，m/s；hmax为最大涌浪高度，m；g为重力加速度，m/s。

距滑坡x点处的涌浪高度估算

h=k1■V0.5 ，   （10）

式中：k1为与距滑坡点距离有关的系数，可由k1-x0.5关系曲线查得（图3）；n为系数，n=1.3～1.5；h为涌浪高度，m。

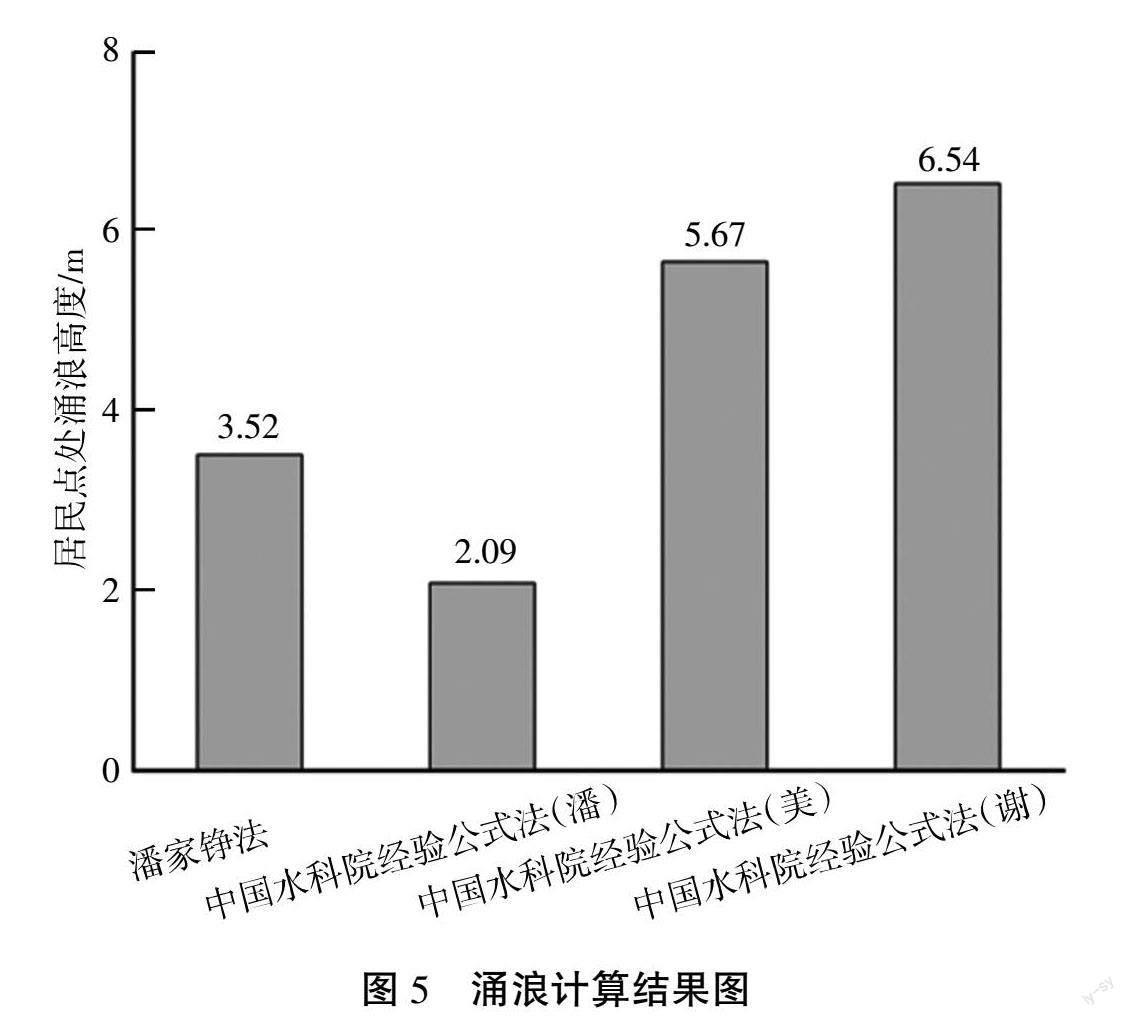
根据上述公式，计算出王家山滑坡在象鼻岭地区的涌浪高度分别为2.09、5.67、6.54 m。

4.3  影响评价

从滑速计算成果来看，如图4所示，王家山滑坡在“暴雨+蓄水”工况下发生整体滑动破坏的最大入水速度，根据潘家铮法、美国土木工程师协会推荐的计算公式、谢德格尔法分别为7.44、13.22、16.81 m/s。3種方法有各自适用的情况，但潘家铮法综合了多种因素，既可以求解直线型滑坡体，又可以求解曲线型滑坡体，更符合实际情况。所以从整体上看，潘家铮法的应用面要广得多，得到的结论也要可靠得多。

从涌浪计算结果来看，如图5所示，象鼻岭居民点处的涌浪，潘家铮法为3.52 m，中国水科院经验公式法分别为2.09、5.67、6.54 m，2种方法计算出的涌浪高度有很大差异，这是因为中国水科院的经验公式中包含了容积效应，但中国水科院的不稳定体体积很小，所以得到的涌浪高度要比中国水科院的低。潘家铮法则是综合了多种因素，得到了较为合理的结论。

象鼻岭居民点场平高程为827 m，仅高出正常蓄水位2 m。根据研究结果，在825 m“蓄水+强降雨”条件下，王家山滑坡发生整体滑移破坏，象鼻岭居民区的涌浪高（潘家铮法）为3.52 m，而在地震条件下，涌浪高将更大，对居民区造成的冲击灾害将有一定的影响。

5  结论

本文以金沙江白鹤滩水电站王家山滑坡为研究对象，基于勘察资料及滑坡基本特征对滑坡整体稳定性进行分析，研究发现在“暴雨工况+蓄水”825 m下，滑坡整体失稳，同时，通过4种不同的计算方法，对象鼻岭居民区的涌浪高度进行了估算，得出王家山滑坡总体失稳破坏时，对居民区的涌浪高度为3.52 m。建议在象鼻岭居民区采取适当的水浪防护措施，或在王家山滑坡上实施工程处理，确保居民区的安全。

参考文献：

[1] 陈世壮，徐卫亚，石安池，等.高坝大库滑坡涌浪灾害链研究综述[J].水利水电科技进展，2023，43（3）：83-93.

[2] 薛宏程，彭杏瑶，马倩，等.考虑阻力作用的碎石土滑坡涌浪数值模拟方法研究[J].人民长江，2023，54（7）：153-58.

[3] 王佳佳，陈浩，肖莉丽，等.散粒体滑坡涌浪运动特征与能量转化规律研究[J].水文地质工程地质，2023，50（4）：160-172.

[4] 马斌，李会平，刘东明，等.窄深河谷库岸滑坡坝前涌浪特性及浪高影响因素[J].南水北调与水利科技（中英文），2023，21（2）：362-370.

[5] 薛宏程，马倩，彭杏瑶，等.基于Herschel-Bulkley流变模型的滑坡涌浪数值模拟方法研究[J].水利学报，2023，54（3）：268-278.

[6] 李东阳，年廷凯，吴昊，等.滑坡-堵江-涌浪灾害链模拟的DEM-CFD耦合分析方法及其应用[J].工程科学与技术，2023，55（1）：141-149.

[7] 郑飞东，王平义，李云.滑坡体散体化对涌浪波动特征的影响[J].水科学进展，2022，33（5）：826-834.

[8] 王梅力，田野，杨胜发，等.水流动力条件下滑坡涌浪初始波浪特征研究[J].水运工程，2022（8）：129-134，171.

[9] 徐卫亚，秦创创，张贵科，等.基于分流比的复杂分汊河道滑坡涌浪远场传播计算方法[J].水利水电科技进展，2022，42（3）：20-24.