基于矢量“隶属度”的模糊控制器结构优化

李战明，张永江，2，韩大红

1.兰州理工大学电气工程与信息工程学院，兰州 730050

2.中国人民解放军69223部队

3.中国铝业股份有限公司兰州分公司，兰州 730060

基于矢量“隶属度”的模糊控制器结构优化

李战明1，张永江1，2，韩大红3

1.兰州理工大学电气工程与信息工程学院，兰州 730050

2.中国人民解放军69223部队

3.中国铝业股份有限公司兰州分公司，兰州 730060

针对传统模糊控制器在控制过程中容易发生规则爆炸的缺点，提出一种基于矢量“隶属度”的模糊控制器结构优化方法。这种优化方法通过对传统模糊控制器的隶属度和模糊等级进行改进，把当前输入量的相对方向和大小等级分别反映在矢量“隶属度”和标量模糊等级上，从而能够大大减少模糊规则数目，降低结构复杂度，提高控制效率。直流电动机的仿真控制效果表明，矢量“隶属度”法优化后的控制器比传统控制器结构简单和误差小，从而验证了这种方法的有效性和可行性。

规则爆炸；结构优化；矢量“隶属度”

1 引言

模糊控制器（Fuzzy controller）规则的数目直接决定了控制器结构的复杂度和控制的精度[1]：规则较少，不能很好地反映控制规律的复杂性，因而不能精确地逼近目标映射；相反，规则较多，容易发生规则爆炸，严重影响控制速度[2]。因此设计结构简单并且能达到性能要求的模糊控制器，就成为众多学者长期致力研究的问题。

目前针对模糊神经网络结构的优化方法比较多，如相似性分析法[3]、经验[4]、遗传算法[5-6]、剪枝法[7-8]和增长法[9]、自组织算法[10]、禁忌搜索算法[11]等。这些方法虽然都对模糊控制规则进行了优化，但是为达到控制精度，又对神经网络部分的权值进行了修正，所以对于单一的模糊控制器这些方法不太适用。聚类算法[12]能够根据初始数据进行模糊等级的确定和隶属度函数参数的确定，这种算法对初始数据依赖程度高，要求其能够反应整个系统特性。

因此本文提出一种基于矢量“隶属度”的模糊控制器结构优化方法，这种优化方法能够根据当前输入量与目标输入量之间的相对方向关系，及时反映在矢量“隶属度”的方向上；由于隶属度已经有方向，因此采用标量模糊等级，只进行大小等级的划分，从而减少了模糊等级数目，最终实现减少模糊规则，降低结构复杂度，提高控制效率的目的。

2 矢量“隶属度”介绍

2.1 基本思路

传统模糊控制器的隶属度为标量，反映了当前输入量属于某个模糊等级的程度，但是并没有反映出当前输入量和目标输入量之间的关系；而这种关系却反映在传统的矢量模糊等级上，这就造成控制器的性能过分依赖模糊等级的划分。

矢量“隶属度”就是对传统模糊控制思路的改进，把隶属度改为矢量，从而矢量“隶属度”既能体现出输入量属于某个模糊等级的程度，又能通过隶属度的方向来表示当前输入量和目标输入量之间的关系，即：

（1）目标输入量大于当前输入量时，对应的隶属度方向为“正/+”，矢量“隶属度”表示为“+μk”，其含义为：在当前输入量小于目标输入量的方向上，输入量属于模糊等级k的程度。

（2）目标输入量等于当前输入量时，对应的隶属度为“零/0”，矢量“隶属度”表示为“0”，其含义为：当前输入量等于目标输入量时，当前输入量对输出变化影响为零。

（3）目标输入量小于当前输入量时，对应的隶属度方向为“负/-”，矢量“隶属度”表示为“-μk”，其含义为：在当前输入量大于目标输入量的方向上，输入量属于模糊等级k的程度。

由于采用的矢量“隶属度”表示法已经反映了当前输入量和目标输入量之间的关系，所以对模糊等级进行标量化处理，这种标量化的模糊等级只进行大小等级的划分，而不牵扯当前输入量和目标输入量之间的关系。如将传统矢量模糊等级：“正大、正中、正零、负零、负中、负大”变为标量模糊等级后，可以表示为：“大、中、零”。

通过这种改进，能够减少模糊规则的数目，降低控制器结构的复杂度，提高控制器的控制效率。

2.2 矢量“隶属度”原理

为了不失一般性，原理介绍采用n输入，单输出的模糊系统：

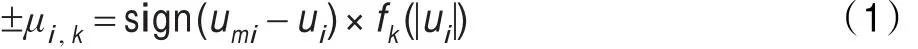
其中，sign(umi-ui)是一个符号函数，根据当前输入量和目标输入量之间的大小关系确定隶属度方向，如公式（2）所示：

umi表示第i个输入量的目标输入量，ui表示第i个输入量当前的输入量，i=1，2，…，n，n为输入量的个数，fk(|ui|)表示第i输入量ui的绝对值对应模糊等级为k时的隶属度函数，k=1，2，…，p，p为输入量的模糊等级数，±μi，k表示第i输入量的模糊等级为k时对应的矢量“隶属度”，“+”号表示当前输入量小于目标输入量的方向上，输入量属于模糊等级k的程度；“0”表示当前输入量和目标输入量相等，当前输入量对输出变化影响为零；“-”号表示当前输入量大于目标输入量的方向上，输入量属于模糊等级k的程度。

2.3 矢量“隶属度”优化能力分析

假设传统模糊控制器有n维输入，且每个输入的模糊等级均为2×m：

传统模糊控制器需要建立(2×m)n条模糊规则。

经过矢量“隶属度”优化后，模糊等级数变为m，在输入没有发生变化情况下，对应的模糊规则为mn条。

经过上面例子可以看出，矢量“隶属度”优化后的模糊控制器的规则数目远远少于传统模糊控制器的规则数目，控制器结构也更加简单。

3 基于矢量“隶属度”的模糊控制器优化设计

3.1 模糊化过程

首先确定各个输入量的目标值，即：umi。其次确定各输入量的模糊等级，选择隶属度函数fk(|ui|)，确定隶属度函数曲线[13]：隶属度函数曲线形状较尖的其分辨率较高，灵敏度较高；相反，隶属度函数曲线形状较缓和的，灵敏度也相对较低。

由于矢量“隶属度”法的模糊化过程和传统模糊化过程不同，既要起到一个精确量向模糊量转换的作用，又要反映出当前输入量与目标输入量之间的关系，采用公式（1）和公式（2）进行矢量“隶属度”的求取。

3.2 模糊推理过程

首先构建模糊规则表，其次根据模糊规则表，将推理得到的输出量的模糊等级组成一个矩阵，然后把模糊等级用对应的隶属度函数中心值替代，就生成模糊规则矩阵F_Rule。

例如在一个两输入一输出模糊等级为三级的模糊控制系统，语言型模糊规则表述如下所示：

将语言型模糊规则转换成模糊规则表，如表1所示。

表1 模糊规则表

根据模糊规则表，生成模糊规则关系矩阵F_Rule：

其中Y(k)-Y(Z)表示输出模糊等级k的隶属度函数中心值与标准输出之间的差值。

3.3 推理计算

3.3.1 计算型模糊推理算法介绍

本文采用计算型模糊推理（Calculation model of Fuzzy Reasoning，CFR）算法[14]进行计算，这种算法是对推理过程进行了改进，在推理过程中同样采用“and”的模糊逻辑进行模糊推理，而在推理计算中采用“+”进行推理计算。推理过程中，根据模糊规则表，通过对输入隶属度的线性数值计算，推理得到输出隶属度。

为了不失一般性，推导采用n个输入的多输入单输出计算型模糊推理系统，第t条语言型模糊推理规则表述如下所示：

其中，x1，x2，…，xn为当前输入变量，Aij表示第i个变量的第j个模糊等级，i=1，2，…，n；j=1，2，…，p，p为输入变量的模糊等级数。yt为输出量，Utk表示在第t条规则中输出量U对应的模糊等级为k，t=1，2，…，r，r为模糊规则数，k=1，2，…，q，q为输出量的模糊等级数。

根据CFR算法，第t条模糊规则的推理计算过程如下所示：

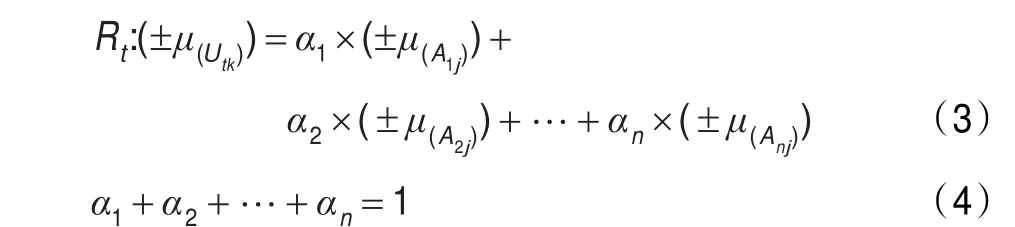
其中，±μ(Aij)表示输入量xi的第j个模糊等级时的隶属度，±μ(Utk)表示在第t条规则中输出量U对应的模糊等级为k时的隶属度，±μ(*)表示带方向矢量“隶属度”运算，αi表示第i个输入量的调节因子，αi的计算参照文献[15]。

3.3.2 推理计算过程

采用CFR算法进行推理计算，依据模糊推理规则，按照公式（3）的计算方法，依次计算表1中的输出隶属度。计算过程如下所示：

在实际计算过程中，推理计算过程如公式（5）所示：

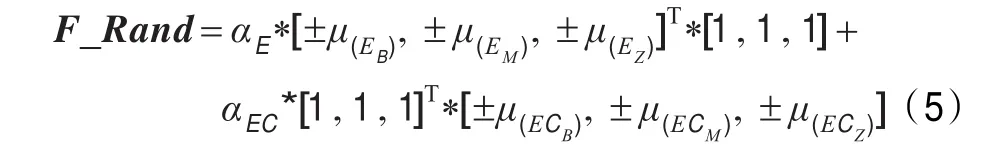
根据公式（5）计算输出隶属度，建立与规则表相对应的推理矩阵F_Rand。

3.4 解模糊过程

矢量“隶属度”优化后的模糊控制器在进行输出解模糊过程中，传统的中心平均法、重心法和最大隶属度法都可以使用。文中介绍了中心平均法解模糊，解模糊公式如式（6）所示，其中解模糊输出的是输出量的变化量，最终输出值如公式（7）所示。

其中，F_Rule是模糊规则关系矩阵，F_Rand是模糊规则矩阵，i为矩阵行数，j为矩阵列数。

3.5 矢量“隶属度”法的模糊控制器优化设计步骤

步骤1根据专家经验确定控制输入量以及输入量和输出量的变化范围，确定目标输入量和标准输出量，确定标量模糊等级，选取隶属度函数。

步骤2制定模糊规则，构建模糊规则表，根据模糊规则表生成模糊规则矩阵F_Rule。

步骤3按照模糊规则，计算推理结果，构建推理矩阵F_Rand。

步骤4中心平均法解模糊计算输出变化量，参照公式（7）求取输出结果。

4 Matlab仿真

为了验证矢量“隶属度”法优化后的模糊控制器具有和传统模糊控制器相同的控制性能，进行两种控制器仿真实验对比，为保证仿真准确性，两种控制器都采用CFR推理算法进行推理计算。仿真在Matlab中进行，选用某种直流电机作为控制对象，其相频特性等效传递函数为[16]：

分别设计传统模糊控制器和矢量“隶属度”模糊控制器，两种模糊控制器的结构参数如表2所示：采用相同输入，相同的隶属度函数曲线以及相同的控制规则，单位阶跃输入，分别对控制器动态输出曲线进行对比。

表2 两种控制器结构参数比较

两种模糊控制器的模糊等级，输入隶属度区间划分和隶属度曲线如图1和图2所示。

根据经验，误差对输出影响直接，相比之下，误差的变化对输出的影响较小，依据文献[8]中介绍方法，调整因子采用式（8）进行计算：

式（8）表示第i时刻误差对输出影响为α(e(i))，对误差变化的影响为α(ec(i))。

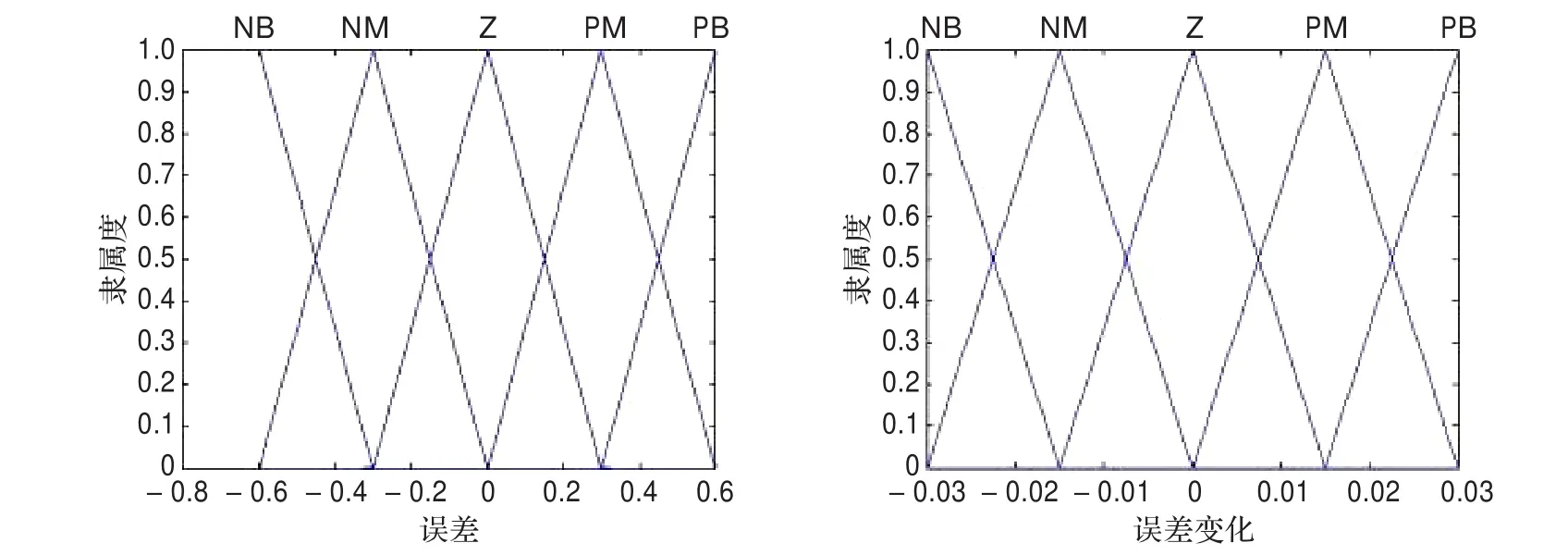
图1 传统模糊控制器输入隶属度划分

给两个控制系统分别加入相同的单位阶跃信号，观察系统的输出和模糊控制器的输出，对控制器参数进行比较。

图3中，（a）图为采用CFR算法的传统模糊控制系统输出，（b）图为采用CFR算法的传统模糊控制器输出；图4中，（a）图为采用CFR算法的矢量“隶属度”模糊控制系统输出，（b）图为采用CFR算法的矢量“隶属度”模糊控制器输出。分别对两种控制器性能进行对比，其中调节时间的误差范围选择为稳态输出的±2%，性能对比如表3所示。

根据表3中的动态数据对比可以看出，采用了矢量“隶属度”优化后的模糊控制器动态性能和传统CFR模糊控制器的动态性能基本没有影响，相反在上升时间、峰值时间和稳态误差上的表现优于传统模糊控制器。

图2 矢量“隶属度”模糊控制器输入隶属度划分

图3 传统模糊系统输出和控制器输出

图4 矢量“隶属度”模糊系统输出和控制器输出

表3 两种控制器性能比较

仿真结果分析：矢量“隶属度”优化法是一种把传统模糊控制器的模糊等级的方向加载在隶属度上的方法，这种方法通过减少模糊等级数目来达到减少模糊规则的目的。仿真结果表明，优化后的模糊控制器和传统模糊控制器相比较，结构更加简单，控制器性能未发生变化，在上升时间、峰值时间和稳态误差上的表现也优于传统模糊控制器。

5 总结

矢量“隶属度”优化法提出了一种新的模糊控制器优化方法，这种优化方法通过对隶属度的矢量化处理和模糊等级的标量化处理来达到减少模糊规则的目的。其中隶属度的方向根据当前输入量和目标输入量之间的大小关系确定，这就相当于把传统模糊控制器的模糊等级的方向加载在隶属度上；标量化处理后的模糊等级数目减半，因此推理规则数目减少，从而达到优化控制器结构的目的。

通过直流电动机的仿真控制效果表明，基于矢量“隶属度”优化后的模糊控制器比传统控制器结构简单，误差小，在一些动态性能上甚至超过了传统模糊控制器。从而证明了这种方法的有效性和可行性。

现阶段关于这种优化方法的报告较少，同时采用的CFR推理算法也刚刚提出，这种方法还不够完善，还需要在接下来的工作中进行更深入的研究和广泛的关注。

[1]Sietsma J，Dow R J F.Neural net pruning：why and how[C]// Proc IEEE Int Conf Neural Networks.San Diego：CA，1988：325-333.

[2]向宇.基于增长剪枝联合算法的模糊神经网络结构优化研究[D].成都：西南交通大学，2009.

[3]Setnes M，Koene A，Babuska R，et al.Data driven initialization and structure learning in fuzzy neural networks[C]// IEEE World Congress on Computational Intelligence，Anchorage，1998.

[4]Lin Y H，Cunningham III G A.A new approach to fuzzy neural system modeling[J].IEEE Trans on Fuzzy Syst，1999，3（2）.

[5]Zhou Z J，Mao Z Y.On designing an optimal fuzzy neural network controller using genetic algorithms[C]//The 3rd World Congress on Intelligent Control and Automation，Hefei，China，2000.

[6]李斌，朱小平，柳润清.基于改进遗传算法的模糊RBF神经网络控制在液压伺服系统中的应用研究[J].机电工程技术，2010，39（1）：66-69.

[7]Leng Gang.An approach for on-line extraction of fuzzy rules using a self-organising fuzzy neural network[J].Fuzzy Sets and Syst，2005，150（2）：211-243.

[8]艾芳菊.一种新的模糊神经网络删剪策略[J].湖北大学学报，2007（4）：346-350.

[9]乔俊飞，韩红桂.神经网络结构动态优化设计的分析与展望[J].控制理论与应用，2010，27（3）：350-356.

[10]乔俊飞，王会东.模糊神经网络的结构自组织算法及应用[J].控制理论与应用，2008，25（4）：703-707.

[11]Glover F，Laguna M.Tabu search[M].Boston：Kluwer Academic Publishers，1997.

[12]宋清昆,赫敏.基于聚类算法的自适应模糊神经网络研究[J].控制工程，2007，14（S1）：14-16.

[13]黄卫华，万康玲，章政.典型模糊控制器的隶属函数设计及分析[J].模糊系统与数学，2010，24（5）：83-90.

[14]李战明，张永江.基于计算型模糊推理算法的模糊控制器设计[J].计算机工程与应用，2014，50（14）：259-264.

[15]李士勇.模糊控制神经·控制和智能控制论[M].北京：电子工业出版社，2010：287-298.

[16]阮毅，陈伯时.电力拖动自动控制系统：运动控制系统[M]. 4版.北京：机械工业出版社，2010：182-245.

LI Zhanming1,ZHANG Yongjiang1，2,HAN Dahong3

1.College of Electric Engineering and Information Engineering,Lanzhou University of Technology,Lanzhou 730050,China
2.Unit 69223 of PLA,China
3.Aluminum Corporation of China Limited Lanzhou Branch,Lanzhou 730060,China

According to shortcomings of traditional fuzzy controller prone to rule explosion in the control process,this paper puts forward a method which is based on vector“membership”fuzzy controller struc-ture optimization.This optimization method is based on the improvement of the traditional fuzzy controller’s membership and degree level.The current inputs relative direction and size gradation reflect in vector“membership”and scalar fuzzy level,thus can greatly reduce the number of fuzzy rules,to reduce the structure complexity and improve the control efficiency.The simulation of DC-motor control effect shows that this kind of controller has a simple structure and smaller error than traditional controller, and also proves the feasibility and effectiveness of this method.

rule explosion;structure optimization;vector“membership”

A

TP181

10.3778/j.issn.1002-8331.1212-0021

LI Zhanming,ZHANG Yongjiang,HAN Dahong.Vector“membership”based fuzzy controller structure optimization. Computer Engineering and Applications,2014,50（21）：74-78.

国家自然科学基金（No.60964003）。

李战明（1962—），男，教授，博士生导师，主要研究方向为复杂系统的建模与控制，智能控制，嵌入式系统研究与开发等；张永江（1985—），男，硕士研究生，主要研究方向为智能控制，控制器性能评估；韩大红（1982—），男，助理工程师，主要研究方向为电器控制。E-mail：274534087@qq.com

2012-12-03

2013-03-11

1002-8331（2014）21-0074-05

CNKI出版日期：2013-03-19，http://www.cnki.net/kcms/detail/11.2127.TP.20130319.1424.006.html