考虑风光不确定性的暂态稳定约束最优潮流模型研究

陈 萍，党 喜，刘龙成，李正浩，王秋杰，刘颂凯

（1.三峡大学电气与新能源学院，湖北宜昌 443002；2.新能源微电网湖北省协同创新中心，湖北宜昌 443002）

0 引言

最优潮流（Optimal Power Flow，OPF）通常用来优化电力系统[1-2]的稳定运行，OPF 的目标是确定每个可调度电厂的发电输出，并使运行成本最小化。由于电力系统的暂态不稳定会产生较高的经济成本，因此研究暂态稳定约束最优潮流（Trnsient Stabiility Constrained Optimal Power Flow，TSCOPF）显得十分重要。暂态稳定性为电力系统承受较大干扰后，电力系统仍能保持稳定运行的能力[3]。TSCOPF 提出一种同时满足系统暂态稳定性与调控经济性的方案，在紧急情况下能够可靠地保证系统的暂态稳定性，并使总发电成本最小化。双碳政策下大规模的新能源接入电力系统中，新能源发电的随机性将会对电力系统的暂态稳定性构成威胁，暂态失稳造成的巨大损失使得电力系统运营商必须提供有效的办法来保证系统的暂态稳定性，研究新能源接入电力系统下的TSCOPF 至关重要。

对新能源不确定性的处理方法[4-6]常见的有场景优化法、鲁棒优化法、机会约束规划法（Chance Constrained Programming，CCP）等。场景优化法通过构建大量确定性的运行场景来分析新能源的不确定性。文献[7]利用蒙特卡洛法模拟不确定量并制定大量确定性场景，缺点是精度受随机抽样质量影响。文献[8]采用场景削减技术减少确定性场景数量以提高计算速率，缺点是考虑的维度较为全面，会因维度过高造成求解难度过大。鲁棒优化法通过考虑不确定参数和变量的范围以及系统对应响应情况，在最不利情况下寻求最优解。文献[9-10]分别采用矩不确定性与假设检验的方法建立不确定集，在一定程度上降低了求解维度，但是其求解精度依赖于根据经验制定的不确定集具有局限性。CCP 法通过将新能源出力约束转化为概率约束，使新能源出力在设定的置信区间下满足运行要求。文献[11]假设风电出力服从高斯假设，将机会约束表达式转换为二阶锥不等式以进行二阶锥规划。文献[12]建立线路潮流极限的机会约束，推导出新能源累积分布函数和累积分布函数的逆函数表达式，但数值积分的过程中可能会放大误差导致模型求解不准确。文献[13]使用四阶多项式近似表达随机变量的累计分布函数，但表达式推导较复杂不利于理解和计算。分析文献[7-13]可知，目前将机会约束转换为确定性约束存在求解复杂性高且准确性不足的问题。

本文针对风光接入电力系统后的不确定性问题，同时为兼顾运行中的经济性和安全性，提出考虑风光不确定性的TSCOPF 模型和求解方法。研究的创新之处在于：（1）利用高斯混合模型（Gaussian Mixture Model，GMM）拟合风光出力，并描述其出力不确定性；（2）提出包含旋转备用机会约束的TSCOPF 模型，在目标函数中增加了由旋转备用产生的高估/低估成本，经济性考虑更全面；（3）基于序列运算方法处理机会约束中的不确定性，对机会约束进行确定性转换，将TSCOPF 模型转化为混合整数线性规划（Mixed Integer Linear Program，MILP）进行求解。未来的研究方向是设计更好的优化求解方法，使求解结果更加准确的同时提高计算效率的目的。

1 不确定性建模

随着新能源接入电力系统的比例不断增加，其出力不确定性对系统的安全稳定运行的不利影响日益明显。因此，针对风光接入后的电力系统，从风光和负荷两方面进行建模。考虑风速、太阳辐射等因素的变化，对风光出力不确定性建模；考虑天气变化、用户需求波动和设备故障等因素的变化，对负荷需求不确定性建模。

1.1 风光建模

光伏出力受辐照强度的影响，可近似认为服从Beta 分布[14]。风电出力受风速影响，可近似认为服从Weibull 分布[15]。目前，对于风光发电的出力不确定性建模需要考虑各种环境因素的影响且建模过程相对复杂，针对此问题本文采用GMM 拟合任意数据分布，且GMM 具有线性不变性的数学性质，有助于描述概率潮流。具体方法是利用GMM 拟合风光预测误差，再通过得到的风光预测误差叠加预测值得到风光出力。GMM 是对不同均值和不同方差的高斯分量设置不同权重进行求和的混合模型，对于多元随机变量y的GMM 模型为：

式中：f(·) 为概率密度函数；Z为高斯分量的总数；az，μz，Dz分别为第z个高斯分量的权重、均值、协方差；ξ为数据维度。

采用GMM 时需保证风光二者相互独立，先确定高斯分量的个数，再求解得到各高斯分量的权重、均值、协方差3 个未知参数，一般通过期望最大化（Expectation Maximum，EM）算法求解未知参数。由于EM 算法初始化设定的参数具有较强的主观因素，如果设定不当将会对结果有较大的影响，故通过获得各高斯分量的熵以获得客观结果，在求解的过程中加入基于熵的惩罚因子，得到最大似然函数maxθ(·) 为：

式中：H为总的迭代次数；分别为第h次迭代中第z个高斯分量的权重、均值和协方差；vz为第z个高斯分量的修正因子；Sz为第z个高斯分量的信息熵。

1.2 负荷建模

由于用户需求量的不同导致负荷具有一定的不确定性，可根据历史信息得到负荷变化的一定规律性和周期性。在电力系统运行过程中，多种因素（包括天气变化、用户需求波动和设备故障等）均可导致负荷不确定性，进而给电网稳定运行带来挑战。以有功功率建模为例（与无功功率建模类似），为有效处理系统的不确定性，本文采用正态分布模拟负荷的不确定性[16]模型为：

式中：Pload为负荷有功功率；σPload为负荷有功功率的标准差；μPload为负荷有功功率的均值。

根据历史数据可得到负荷预测误差的概率分布函数，预测误差叠加预测值后可得到负荷有功功率实际值为：

2 TSCOPF模型构建

TSCOPF 模型一般包含使运行成本最小化的目标函数、潮流平衡等式约束、对发电机机组及线路的功率上下限的不等式约束、暂态稳定约束和旋转备用约束。

2.1 目标函数

含风光接入的电力系统中，当新能源的实际发电量高于预估发电量，通过减少火力发电机出力或者弃风弃光来维持系统稳定，这部分产生的成本称为低估成本。高估成本是用于弥补预计和实际的有功功率差额的火力发电机发出的有功功率成本。本文运行成本包含火力发电机燃料成本及高、低估成本，使运行成本最小化的目标函数F为：

式中：t为运行时刻；T为目标函数求解范围的总时刻；nG为火力发电机的总数；为第i台火力发电机燃料成本函数；为t时刻第i台火力发电机的有功功率；nW为风力发电机的总数；为第e台风力发电机低估成本函数；为t时刻第e台风力发电机的有功功率；为第e台风力发电机高估成本函数；nPV为光伏板的总数；为第g台光伏板低估成本函数；为t时刻第g台光伏板的有功功率；为第g台光伏板高估成本函数。

第i台火力发电机燃料成本函数，第e台风力发电机风电低估成本函数、风电高估成本函数表达式为：

2.2 潮流平衡等式约束

建立潮流平衡等式约束为：

2.3 不等式约束

本文所提TSCOPF 模型在CCP 模型基础上建立，不等式约束需要满足其发生的概率在一定置信水平上成立的条件。其中不等式约束包括对于火力发电机出力有功、无功上下限的约束以及对线路功率上限的约束，其表达式为：

式中：Pr(·) 为满足不等式成立的概率函数；分别为t时刻第i台火力发电机有功功率的下限和上限；分别为t时刻第i台火力发电机无功功率的下限和上限；为t时刻第l条线路的有功功率；为t时刻第l条线路可承受的最大有功功率；分别为设定的火力发电机有功功率、发电机无功功率、线路有功功率置信水平。

2.4 暂态稳定约束

暂态稳定约束用于判断系统的暂态稳定性是否满足运行要求。本文利用卷积神经网络挖掘电力系统参数和暂态稳定指标（Transient Stability Index，TSI）之间的映射关系构建暂态稳定约束，TSI根据发电机最大功角差判断系统的暂态稳定性，TSI用物理量ηTSI表示。当ηTSI＞0 时认为系统暂态稳定，反之为系统暂态失稳。本文将暂态稳定约束定义为ηTSI＞0，ηTSI表达式为：

式中：δmax为设定暂态稳定过程中的任意2 台发电机之间的最大功角差。

2.5 旋转备用约束

为解决新能源不确定性导致的系统运行失稳问题，可通过增加备用容量等措施维持系统稳定运行[17-18]。本文采用火力发电机的旋转备用容量弥补风光预测误差和负荷误差的总和，以克服不确定性造成的系统失稳。旋转备用约束为：

3 TSCOPF模型确定性转换与求解

本文所提TSCOPF 模型采用序列运算处理变量的不确定性问题，先将风光的连续型概率函数离散化得到离散概率序列[19-20]，然后通过序列运算处理得到净负荷的离散概率序列，再引入0-1 变量将概率形式的机会约束转换为满足条件的概率和的形式，进而转换为确定性约束，最后将TSCOPF 模型转换为MILP。

3.1 序列运算

序列运算基于信号处理理论，具有概念清晰和计算简单的显著优点。本文使用序列运算中加法卷积和减法卷积运算[21-23]来对离散概率序列进行处理，其中将概率密度函数离散化得到离散概率序列表达式为：

式中：q为离散序列的步长；x为变量；k为第k个离散序列；K为离散概率序列总数。

在处理得到净负荷的预测误差的离散概率序列时，首先将风、光、负荷建模得到的概率密度函数转换为风、光、负荷3 组离散概率序列，再由风、光预测误差的离散概率序列进行加法卷积得到风、光误差的联合概率序列，然后通过负荷预测误差的离散序列和风、光误差的联合序列进行减法卷积运算得到净负荷的预测误差的离散概率序列{b(1),...,b(k)}。其中净负荷的预测误差的离散概率序列关于q和k的对应关系为：当输出功率为kqMW 时，其对应的概率为b（k）。

3.2 机会约束确定性转换

为提高求解效率并方便求解器求解，对机会约束中非线性项不确定性进行线性化确定性转换[24-25]。对于火力发电机，依据参考文献[20]得到其离散概率序列。以线路功率不等式约束为例，对风光以及火力发电机进行加法卷积得到节点有功注入的离散概率序列，再与各节点功率转移分布因子矩阵结合得到线路潮流的序列，如果功率转移分布因子为正则进行加法卷积运算，否则进行减法卷积运算。最终引入0-1 变量，将概率形式转换为概率和的形式进行确定性转换[26-27]。

以正旋转备用约束为例，引入t时刻第k个离散序列对应的的0-1 变量φk,t，其表达式为：

当满足旋转备用大于等于净负荷实际与预测误差值条件时变量φk,t取1，可将正旋转备用机会约束转换为概率值之和，即：

但由于变量φk,t的表达式并不适用于MILP 求解，引入1 个极大的正数ω将式（18）再次转换为：

式中：ι为1 个极小的正数。

3.3 模型求解过程

TSCOPF 模型求解过程，如图1 所示。

图1 TSCOPF模型求解过程Fig.1 TSCOPF model solving process

本文提出的TSCOPF 模型求解过程具体如下：

1）对风、光、负荷建模。根据历史数据，求解得到风光的GMM 所需参数值，得到风光出力预测误差概率函数，并对负荷波动利用正态分布进行建模。

2）搭建TSCOPF 模型。根据式（7）—式（15）搭建TSCOPF 模型，并基于电力系统的历史数据训练卷积神经网络判断电力系统的暂态稳定性。

3）生成风、光、负荷离散概率序列并通过序列运算得到净负荷序列。设定初始的离散步长值，将风、光预测误差及负荷波动概率分布函数转化为离散概率序列，再通过序列运算生成净负荷的概率序列。

4）机会约束确定化转换。利用净负荷的概率序列将机会约束转化为确定性约束，将所提基于机会约束的TSCOPF 模型转换为更易求解的MILP。

5）输入参数。输入系统的基本参数，包含各节点电压相角、电压幅值、各发电机出力等数据。

6）Gurobi 求解器求解。使用Gurobi 求解器求解转换后的MILP 模型，如果得到最优解，则输出系统的最小成本并终止求解；否则，更新置信水平和负荷重新进行求解。

4 算例分析

在改进的IEEE 39 节点系统上进行仿真测试，IEEE 39 节点系统如图2 所示。其中，G1—G10 为10 台火力发电机，在节点37，39 处将G1，G4 分别替换为装机容量为350 MW 的风力发电机W1，W2，在节点33，35 处将G7，G8 分别替换为装机容量为100 MW 的光伏板PV1，PV2。各节点负荷预测误差服从预测值为期望值、标准差为负荷预测值10%的正态分布，预测值由预测模型训练得到。由于不等式约束的置信水平需维持较高的标准，因此均取值为90%，设离散化步长为1 MW。假定在节点16 与节点24 线路连接处发生三相短路故障，并于0.16 s后切除该故障。硬件环境为Intel（R）Core（TM）i3 CPU 3.2 GHz，内存为4 GB，调用MATLAB 中Gurobi商业求解器进行求解。

图2 IEEE 39节点系统Fig.2 Diagram of IEEE 39-bus system

4.1 GMM拟合效果

评价GMM 拟合精度，通常使用以下2 个常用指标：平均绝对误差（Mean Absolute Error，MAE）、均方根误差（Root Mean Square Error，RMSE），其量值分别用EMA，ERMS表示。使用Elia[28]数据库中提供的风、光数据，分别采用Beta 分布模型、高斯分量个数取5 的GMM-5 模型、高斯分量个数取6 的GMM-6模型、改进EM 算法的GMM-6 模型、Weibull 分布模型对10 h 光伏、风电不确定性进行拟合。分布模型拟合精度如表1 所示。

由表1 可知，与利用Beta 分布建模和Weibull分布建模相比，采用GMM 建模得到的EMA，ERMS值更小，说明GMM 的拟合结果更准确。且本文使用改进后的EM 算法求解得到的GMM-6 相较于未使用改进后的EM 算法求解得到的GMM-6，其EMA，ERMS的值更小，说明采用改进后的EM 算法求解后的拟合结果更准确。

4.2 可靠性验证

新能源接入电力系统后不确定性会加强，适当增加备用容量可弥补预测偏差带来的影响。为验证本文所提方法应对风光不确定性因素的效果，用等容量的火力发电机组替换风光，替换前后求解的旋转备用容量如图3 所示。

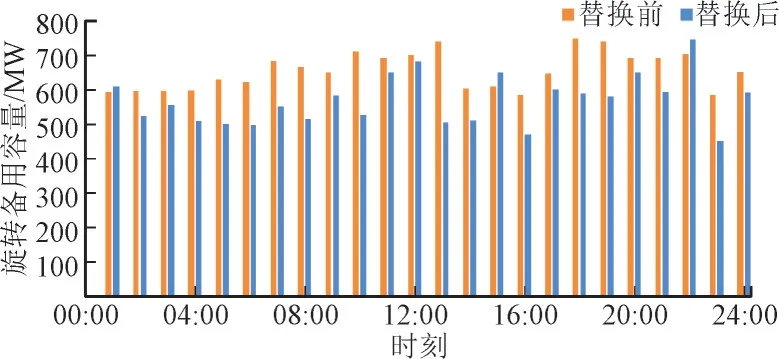
图3 替换前后求解的旋转备用容量Fig.3 Rotating reserve capacity solved before and after replacement

由图3 可知，在大多数时刻下，替换前求解得到的旋转备用容量更多，说明由于接入风光的系统中求解得到的备用容量计入了准确度较高的风光预测误差，从而能够有效应对风光的不确定性，说明本模型求解结果能够保证接入风光后系统的运行可靠性。

4.3 不同置信水平影响

置信水平的选择对于模型求解具有一定的影响，分别在80%，85%，90%，95%的置信水平下求解得到其目标函数得到的成本分别为9.337×106元，9.358×106元，9.479×106元，9.683×106元。因此，随着置信水平的增大，成本也不断增大。造成这种现象的原因是，更高的置信水平会导致更大的旋转备用容量需求，以应对风、光出力和负荷预测误差的波动。说明置信水平的设定会直接影响到系统的成本和安全性，因此调度人员需要在可靠性和经济性之间进行权衡，并根据实际情况选择适当的置信水平。

4.4 暂态稳定优化效果对比

为验证本文所提TSCOPF 模型在应对风光不确定性时对系统暂态稳定性提升的效果，将其和传统TSCOPF 模型优化后的系统暂态稳定状态进行比较，根据火力发电机功角差构建的ηTSI判断系统的暂态稳定状态。在相同的故障情况下进行仿真，仿真时长设置为20 s，在该故障情况下系统失稳功角图如图4 所示。

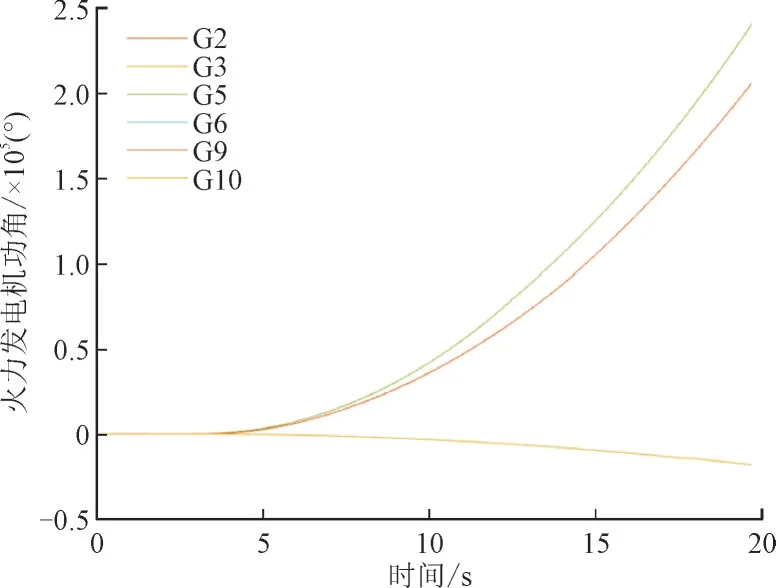
图4 失稳功角图Fig.4 Diagram showing angle instability

由图4 可知，故障情况下在仿真失稳后随着时间的延续，功角值仍会不断的增加，最终任意2 台发电机最大功角差远超360°，说明此时系统处于较严重的暂态失稳状态。

通过传统TSCOPF 模型和本文TSCOPF 模型对系统运行方式进行优化求解，不同TSCOPF 模型求解后功角图如图5 所示。

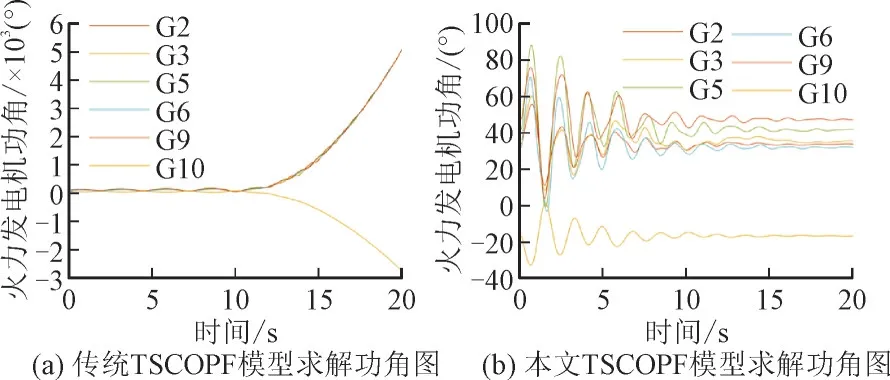
图5 不同TSCOPF模型求解后功角图Fig.5 Diagram showing power angle after operationmode optimization by different TSCOPF models

由图5 可知，图5（a）中传统TSCOPF 模型求解得到系统的发电机功角差有所缩小，但是系统ηTSI＜0，系统仍不稳定，说明传统TSCOPF 模型不能很好处理不确定性。图5（b）中通过本文TSCOPF 模型求解后发电机功角差在180°范围内，ηTSI＞0，系统暂态稳定。说明本文TSCOPF 模型能够有效提升系统的暂态稳定。

5 结论

本文针对风光接入电力系统后的不确定性问题，同时为兼顾运行中的经济性和安全性，提出考虑风光不确定性的TSCOPF 模型和求解方法。通过算例分析得到以下结论：

1）利用GMM 模型拟合风光分布，比单一的分布模型拟合效果更加准确。通过在EM 算法最大似然函数中引入熵概念，求解得到的GMM 模型结果更加准确。

2）将火力发电机组替换为新能源机组后，求解得到的旋转备用容量增加，说明所提方法能较好应对风光不确定性，使系统运行更加可靠。

3）置信水平越高说明安全性越强，但经济成本也会相应增加，设定合适的置信水平可较好平衡经济性和安全性二者之间的需求。

4）本文所提TSCOPF 模型相比传统TSCOPF 模型能更好应对风光的不确定性，维持系统的暂态稳定。