凸多面体的空间分割定理*
——从新教材一道课后习题引发的探究
北京师范大学贵阳附属中学(550081) 李鸿昌
贵阳市乌当中学(550018) 陈启健
我们知道,一个平面将空间分成2 个部分,两个平行平面将空间分成3 个部分,两个相交平面将空间分成4 个部分.那么,一个凸多面体能将空间分割成几个部分呢? 是否具有一般的公式可以直接求解呢? 本文从新教材一道课后习题出发,来探究这个问题.
1 课后习题与正方体分割空间问题
2019 年人教A 版《数学必修第二册》132 页习题5:
正方体各面所在平面将空间分成几部分?
解析如图1 所示,将正方体各面所在的平面进行延展,按规律可数得,正方体各面所在的平面将空间分成27个部分.
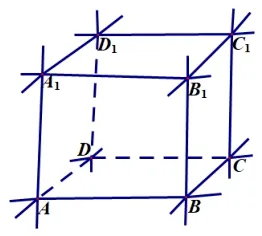
图1

图2
评析反过来,正方体的顶点数V=8,面数F=6,棱数E=12,正方体本身T=1,分成的27 个部分可表示为P=V+F+E+T.那么,这个公式对其他的凸多面体是否也成立呢? 是否具有一般性呢?
2 凸多面体的空间分割定理
定理如果一个凸多面体(最简单的为四面体)的棱数为E,那么它将空间分成的部分数为P=2E+3.
证明设凸多面体T的顶点数为V,面数为F,棱数为E,将T的各面延展得到一个空间分图.经过研判,多面体T的每一个面,每一条棱,每一个顶点“向外”都对应着空间的一个部分,加上多面体T本身,则T将空间分成的部分是P=V+F+E+1.由欧拉定理(其证明见文[1])知V+F-E=2,∴P=V+F+E+1=2E+3.
评析定理的结论只与凸多面体的棱数有关,且简洁、漂亮,给解决问题带来了很大的便利.
3 定理的特例
案例1 四面体棱数E=6,则它将空间分成P=2×6+3=15 个部分.
案例2 正方体的棱数E=12,则它将空间分成P=2×12+3=27 个部分.
案例3 五棱锥的棱数E=10,则它将空间分成P=2×10+3=33 个部分.
4 定理的应用
应用1 一个凸多面体的顶点数为10,面数为7,则它将空间分成( )个部分.
A.30 B.31 C.32 D.33
解析∵V=10,F=7,V+F-E=2,∴E=10+7-2=15,故它将空间分成了P=2×15+3=33 个部分,选D.
应用2 一个凸多面体不可能将空间分成的部分数是( ).
A.35 B.39 C.43 D.46
解析由P=2E+3知S是奇数,故选D.
应用3 一个凸多面体将空间分成35 个部分,设它的顶点数为V,面数为F,则的最小值为____,此时,该凸多面体的顶点数V=____,面数F=____.试画出满足这个条件的多面体(答案不唯一).

