基于滑动窗口含负项的高效用模式挖掘

武 妍，荀亚玲，马 煜

(1.太原科技大学 经济与管理学院，山西 太原 030024；2.太原科技大学 计算机科学与技术学院，山西 太原 030024)

0 引 言

传统基于支持度框架的频繁模式挖掘，因其仅考虑高频模式导致一些真正有价值但支持度较低的模式被忽略。因此，考虑“效用”的高效用模式挖掘(high utility pattern mining，HUPM)被提出并取得了很大进展[1-3]，然而它们都假设数据是静态的。而在互联网时代，数据大都是以流的形式产生，流数据连续、快速且不受限制的特征使流中的每个项只能被检查一次，传统的增量挖掘方式[4-9]已不能满足流数据对时效性的要求，且现实场景中一般认为最新数据比旧数据对于决策更重要，而增量挖掘中并不区分新旧数据。目前，流数据处理模型主要包含3种：基于衰减窗口[10，11]、基于界标窗口[12]、基于滑动窗口[13-15]。衰减模型的局限性在于很难确定一个合适的衰减函数或衰减率；界标窗口方法的局限性是需要长时间捕获数据信息，数据量庞大。滑动窗口模型只针对窗口内最近批次的数据块挖掘高效用项集，消除了过期数据的影响，有效提高了挖掘效率。

此外，传统HUPM仅考虑了项效用值为正的情况，为在挖掘过程中不丢失某些有价值的结果集，Chu等[16]提出的HUINIV(high utility itemsets with negative item values)-Mine算法是第一个考虑带有负效用的HUPM算法，由两阶段算法扩展而来。Lin等[17]提出FHN(faster high-utility itemset miner with negative unit profits)算法，利用效用列表来有效地挖掘高效用项集，同时利用事务加权效用和剩余效用来修剪搜索空间，但可能会生成不在数据库中的模式集。Sun等[18]亦提出基于列表结构的可挖掘含负项的效用项集挖掘算法。总之，基于效用列表结构的单阶段算法被认为是更有效的，其主要局限性在于创建和维护列表的成本非常昂贵。

针对以上局限性，本文定义了一种新的效用列表结构以维护挖掘最近批次高效用模式集所需的所有信息，避免了数据库的重复扫描；并基于该列表结构，提出一种基于滑动窗口含负项的高效用模式挖掘算法(high utility pattern with negative unit profit based on sliding window，HUPN_SW)，在不产生候选效用模式集的情况下，直接挖掘出高效用模式集。

1 问题陈述及相关定义

1.1 问题描述

给定一组有限的项I={i1，i2，…，im}，每个项目ip(1≤p≤m) 的单位利润为p(ip)。项集X是k个不一致项 {i1，i2，…，ik} 组成的，其中ij∈I，1≤j≤k，k是X的长度，长度为k的项集称为k项集。一个事务数据库D={T1，T2，…，Tn} 中包含一组事务，其中每个事务Td(1≤d≤n) 都有唯一的标识符Tid。用q(ip，Td) 表示在交易Td中项目ip的购买数量。一个示例数据库如图1所示，表1为各项目对应的利润，即外部效用。

图1 示例数据库

基于滑动窗口的技术，将一个给定的流数据库分成几个包含相等数量事务的批。假设D为流数据库。在滑动窗口模型中，根据事务的生成时间，D可以被分割成多个批次。该事务流被划分为等长的4个批次(图1的示例数据库)。每一批B={T1，T2，…，Tn} 是一组事务，n为每批的大小；W={B1，B2，…，Bm} 是一组称为窗口的批次，m表示窗口的大小。每个批次和窗口的大小由用户指定。示例中，有两个滑动窗口，W1={B1，B2，B3} 和W2={B2，B3，B4}，每批的大小为2，一个窗口的大小为3。W1是初始滑动窗口，W2是滑动W1的结果，通过删除最旧的批次并插入最新的批次，即随着时间的推移，最老的一批B1被移出，B4被新添加到窗口中，W2成为当前窗口。使用滑动窗口技术的目标是不必扫描整个数据库，只从当前窗口中挖掘所有的高效用项集，从而提高挖掘效率。

1.2 基本定义

定义1 项目效用[1]：在事务Td中项目ip的效用表示为U(ip，Td)，定义为

U(ip，Td)=p(ip)×q(ip，Td)

(1)

式中：p(ip) 为项目ip的外部效用，q(ip，Td) 为项目ip在事务Td中的数量。例如，图1中项目A在事务T1中的效用U(A，T1)=(-3)×1=-3。

定义2 项集在事务中的效用[1]：项集X在事务Td中的效用表示为U(X，Td)，定义为

(2)

例如，图1中U(AC，T1)=-3×1+4×2=5。

定义3 项集的效用[1]：项集X的效用表示为U(X)，定义为

(3)

式中：Td为包含项集X的事务。例如，图1中U(AC)=U(AC，T1)+U(AC，T2)+U(AC，T3)+U(AC，T6)+U(AC，T8)=5+10+(-5)+7+10=20。

定义4 事务效用[1]：事务Td的效用表示为TU(Td)，定义为

(4)

例如，图1中TU(T1)=U(A，T1)+U(C，T1)+U(D，T1)=(-3)+8+4=9。

定义5 事务加权效用[1]：项集X的事务加权效用表示为TWU(X)，定义为

(5)

例如，图1中TWU(A)=TU(T1)+TU(T2)+TU(T3)+TU(T6)+TU(T8)=9+20+21+18+18=86。

定义6 高效用项集[1]：给定项集X及用户指定的最小效用阈值Minutl，若U(X)≥Minutl，则称项集X为高效用项集，否则为低效用项集，低效用项集的超集不可能是高效用项集。

为了挖掘高效用项集，同时考虑正、负单位利润，则对将相关的概念进行重新定义如下：

定义7 重定义事务效用[19]：事务Td的具有正外部效用的项目效用之和为重定义事务效用，表示为PTU(Td)，计算公式为

(6)

例如，图1中PTU(T1)=8+4=12。

定义8 重定义事务加权效用[19]：项集X的重定义事务加权效用表示为PTWU(X)，定义为

(7)

例如，图1中窗口W1中PTWU(C)=12+26+30+26+17+18=129。

TWU用于修剪搜索空间，但是只有当项目的外部效用值为正值时，这些属性才有效。所以基于重新定义的交易效用PTU，进而计算项集的PTWU。

定义9 窗口中项集的效用[20]：窗口W中项目X的效用表示为U(X，W)，通过将X在属于W的所有事务中的效用相加来计算。计算公式为

(8)

式中：Td为窗口W中包含项集X的事务。例如，图1中U(AC，W1)=U(AC，T1)+U(AC，T2)+U(AC，T3)+U(AC，T6)=5+10+(-5)+7=10。

2 算法描述及实例描述

HUPN_SW算法首先要构造一种效用列表结构：滑动窗口正负效用列表(positive and negative with sliding window utility-list，PNSWU-List)，PNSWU-List定义如下：

定义10 PNSWU-List：数据库D中项集X的PNSWU-List是一组元组，每个包含X的事务T都有一个元组，每个元组包含以下4个字段：①Tid，事务标识符；②putil，事务中的正效用；③nutil，事务中的负效用；④rputil，事务中只有正效用值的剩余效用。

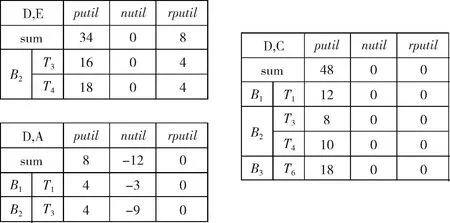
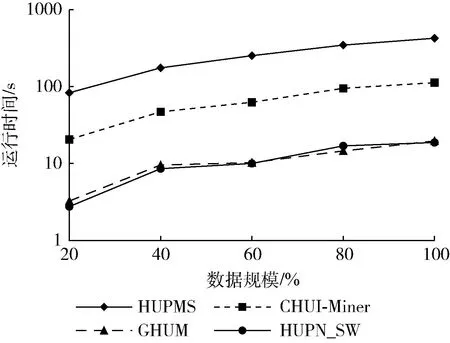
对于任意项集X，都有U(X)=putil(X)+nutil(X)。X中效用值为正的项目只能增加X的效用，而效用值为负的项目只能降低X的效用，因此有：nutil(X)≤U(X)≤putil(X)；若U(X)+rputil(X)

HUPN_SW算法的框架由以下部分组成：扫描数据库，计算每个项目的PTWU且依PTWU值升序排列；构造1-项集PNSWU-List；列表两两组合，进而挖掘高效用项集；进行窗口滑动，挖掘下一个窗口的高效用项集。

基于滑动窗口含负项的高效用项集挖掘算法步骤如下：

步骤1 窗口W1被最近的批次填满，从该窗口中找到高效用项集。首先对数据库进行第一次扫描，由于W1={B1，B2，B3}，第一批B1={T1，T2}，按照事务标识符的顺序，T1在T2之前被处理。项目的PTWU值可以根据属于B1，B2和B3中的交易计算，即项目的PTWU值仅根据属于当前窗口的事务来确定。根据定义计算事务效用TU，正事务加权效用PTWU。

假设事务数据库最小效用阈值Minutl为45，从表2可以得到，由于PTWU(F)

表2 W1项目及其PTWU

事务数据库中的项目的事务加权效用PTWU排序规则：负项事务加权效用总是在所有正项之后；正项事务加权效用升序排序；负项按其绝对值升序排序。即交易中的项目顺序为B、D、E、C、A。

算法1：对事务加权效用PTWU排序

输入：交易数据库D，最小效用阈值Minutl，批次大小n，窗口大小m

输出：依PTWU值排序的项目序列。

(1)根据数据的生成时间,用事务将D分割为多个批次Bk

(2)for each batchBk∈Ddo

(3) for each transactionTd∈Bkdo

(4) for each itemX⊆Td

(5) 计算PTWU(X)

(6) end for

(7) ifPTWU(X)≥Minutl

(8) 对PTWU升序排序,正项在前,负项在后

(9) 依PTWU值升序输出项目序列

(10) end if

(11) end for

(12) 构建项集列表,挖掘高效用项集,然后进行窗口滑动

(13)end for

步骤2 构造1-项集列表：putil和nutil分别是当前正负项目数目与利润的乘积；rputil是当前PTWU升序排序项目之后的项目利润总和(正利润)。根据PTWU的顺序，首先访问的是B的列表。例如B列表中有在批次B2里的事务T3，T4和批次B3中的事务T5，putil(T3)=B.num×B.profit=2×2=4，nutil(T3)=0，rputil(T3)=C.num×C.profit+D.num×D.profit+E.num×E.profit=1×4+2×2+4×3=20，由于B的利润是正值，nutil是负项目数和利润的乘积，所以nutil(T3) 为0，rputil是按PTWU升序排列的模式项目B后的其余项目(即D、E、C)的利润总和，rputil(T3) 为20。同法可得出：putil(T4)=4，nutil(T4)=0，rputil(T4)=22；putil(T5)=6，nutil(T5)=0，rputil(T5)=10；sum(putil)=putil(T3)+putil(T4)+putil(T5)=14；sum(nutil)=nutil(T3)+nutil(T4)+nutil(T5)=0；sum(rputil)=rputil(T3)+rputil(T4)+rputil(T5)=52。项目D作为下一个访问的列表。当所有属于B1，B2和B3的事务以相同的方式处理完成后，可得到如图2所示的1-项集的PNSWU-List列表。

图2 1-项集的PNSWU-List

检查数据库中的列表以及和其它的列表组合是否可以生成高效用模式集。B列表中，psum+nsum为14，小于Minutl，则{B}不是高效用项集，psum+rpsum为14+52=66，大于Minutl。然后对列表B进行进一步的组合处理。同理{D}、{E}、{A}也不是高效用项集。C列表中，psum + nsum为50，大于Minutl，则{C}为高效用项集。对列表D，E，C，A进行进一步组合处理。

步骤3 将列表和其它的列表进行组合。

B，D，E，C列表中psum+rpsum都大于Minutl，因此B，D，E，C的递归列表构造是为了构造较长模式的列表而进行的。

现构造了如图3所示的以{D}作为前缀项的2-项集，为了组合D和E的列表，先比较两个列表的条目，找到C和E的公共事务。两个列表的公共事务是T3，T4。因此，构建了一个DE的PNSWU-List列表，并在该列表中创建了T3，T4两个条目。D和E是长度为1的模式，所以它们的公共前缀模式是空。构造2-项集列表中两个1-项集列表组合：putil和nutil为两相同项集之和；rputil设置为PTWU序列中靠后的项目rputil的值。比如，DE列表中putil(T3) 等于D列表中putil(T3) 与E列表中putil(T3) 的和，即12+4=16，DE列表中rputil(T3) 等于E列表中rputil(T3) 的值，即4，同理DE列表中putil(T4)=6+12=18，rputil(T4)=4。

图3 以{D}为前缀项的2-项集的PNSWU-List列表

DE列表中psum+nsum为34，小于Minutl，则{DE}不是高效用项集；psum+rpsum为42，小于Minutl，则不能通过将列表DE与其它项目的列表组合来生成任何高效用模式集。

同理可得出，{DA}不是高效用项集，且不能通过将列表DA与其它项目的列表组合来生成任何高效用模式集。DC列表中psum+nsum为48，大于Minutl，因此，{DC}是高效用项集，对列表DC进行进一步的组合处理。

进一步构造3-项集PNSWU-List列表。构造3-项集列表中两个2-项集列表组合：putil和nutil为两相同项集之和与两者交集项目的差值；rputil设置为PTWU值后边的rputil的值。比如，DCE列表中putil(T3) 等于DC列表中putil(T3) 与DE列表中putil(T3) 的和与D列表中putil(T3) 值的差，即16+8-4=20，DCE列表中rputil(T3) 等于0，同理DCE列表中putil(T4)=18+10-6=22，rputil(T4)=0。得到如图4所示的以{D}作为前缀项的3-项集。

图4 以{D}为前缀项的3-项集的PNSWU-List列表

DCE列表psum+nsum为42，小于Minutl，则{DCE}不是高效用项集。psum+rpsum为42，小于Minutl，不能通过将列表DE与其它项目的列表组合来生成任何高效用模式集。同理可得出{DCA}也不是高效用项集，并且也不能通过与其它项目的列表组合来生成任何高效用模式集。至此，以{D}为前缀的模式挖掘结束，得到高效用项集{DC}。

算法2：列表的组合

输入：一系列列表，最小效用阈值Minutl

输出：高效用项集

(1)输入一系列列表

(2)for each list

(3) if psum+nsum≥Minutl

(4) 输出高效用项集

(5) else if psum+rpsum≥Minutl

(6) do 列表两两组合,列表x.Td=列表y.Td

/*构造k-项集列表xy,k≥2*/

(7) if k=2

(8) xy.putil=x.putil+y.putil,

(9) xy.nutil=x.nutil+y.nutil,

(10) xy.rputil=y.util

(11) else

(12) xy.putil=x.putil+y.putil-x∩y.putil,

(13) xy.nutil=x.nutil+y.nutil-x∩y.nutil,

(14) xy.rputil=y.util

(15) end if

(16) while psum+rpsum

(17) end if

(18) end if

步骤4 得到窗口W1的高效用项集后，进行窗口滑动。

当有新批次数据到达时，需要从列表中删除最老批次的数据，如图1所示，按批号将条目分组，可以简单地从所有列表中删除属于最早一批的条目，即删除最老的批次B1，新插入B4。然后重复对窗口中的数据按以上的步骤进行处理，得到高效用项集。如此往复，直到数据集中没有更多的批次。

3 实验结果及分析

3.1 实验环境及数据集

为验证提出算法HUPN_SW的性能，选择具有代表性的GHUM[19]、CHUI-Miner[21]、和HUPMS[22]进行对比分析。

实验平台：实验所使用的系统是64位的Windows 10，CPU为英特尔i7处理器，内存8 GB。

实验数据集：实验中使用了2个标准的数据集Retail、Connect，分别来源于匿名比利时零售商店的客户交易(source FIMI：http：//fimi.ua.ac.be/data/)和基于UCI connect-4数据集(source：FIMI)。数据密度分别为0.06%，33.33%。这2个数据集的数据特性见表3，其中包括：交易总数；同项目的数量；平均交易长度；最大交易长度。实验中2个数据集都没有提供对应的数量和单位利润。在这里，项目的外部效用是采用对数正态分布在0.01～10之间产生的，项目的内部效用是随机在1～5之间产生的。

表3 数据集特征

在基于滑动窗口的实验中，将数据集划分为若干个窗口，包括固定批次数量。首先，在W1内进行挖掘，然后，当前窗口从W1滑动到W2。滑动过程中，淘汰了一批在W1中过时的批次，并插入一个新的批次，在W2内进行挖掘。

3.2 实验结果分析

3.2.1 效用阈值对算法性能的影响

本实验分别给出了在不同最小效用阈值时下4种算法在数据集Retail和Connect上的运行性能，实验结果如图5、图6所示。运行时间性能是在执行所有窗口的挖掘过程的总运行时间。

图5 不同支持度下算法运行时间(Retail数据集)

图6 不同支持度下算法运行时间(Connect数据集)

从图5和图6可以看出，4种算法都随着最小效用阈值的增大，运行时间也逐渐变小。因为最小效用阈值越大，算法产生的高效用项集就越少，运行时间就越小。在Retail数据集中，HUPMS算法和CHUI-Miner算法耗时明显多于HUPN_SW算法，GHUM算法与HUPN_SW算法相差不大；在Connect数据集中，HUPMS算法运行时间明显高于其它3种算法。原因是：HUPN_SW算法与GHUM算法采用相似的列表结构，而CHUI-Miner算法执行需要两次扫描数据库来构建效用列表，HUPMS算法则需要执行两次扫描数据库构建树结构。

3.2.2 可扩展性测试

该组实验通过增加数据集规模验证了4种算法的可扩展性能。选取数据集总量的20%、40%、60%、80%、100%，在相同的最小效用阈值情况下，通过数据交易总数的变化进行算法运行时间分析，实验结果如图7、图8所示。

图7 数据集Retail上算法的可扩展性

图8 数据集Connect上算法的可扩展性

从图7和图8可以清晰地看出，随着数据集占总数的比例越来越多，各算法运行时间也逐渐增加。4种算法在数据集Connect的可扩展性表现的更佳。原因是：数据集Connect的稀疏密度明显大于数据集Retail的稀疏密度。挖掘稀疏密度大的数据集运行时间更小。

3.2.3 不同批次大小的运行时间

本小节显示了在相同的最小效用阈值，不同批次大小下，算法HUPMS和算法HUPN_SW在数据集Retail和数据集Connect的运行时间测试结果。在数据集Retail上，批次大小的尺寸从10 K逐渐增大到14 K；数据集Connect上，批次大小从11 K逐渐增大到15 K，实验结果如图9、图10所示。

图9 不同窗口下算法运行时间(Retail数据集)

图10 不同窗口下算法运行时间(Connect数据集)

从图9和图10可以看出，算法的运行时间随着批次大小的增大而减小。原因是，批次大小越大，数据集产生的窗口数相对越少，算法对给定的数据集进行更少次数的挖掘。HUPN_SW算法在不生成候选模式的情况下执行挖掘过程，消耗的运行时间更少。

3.2.4 挖掘结果的准确性实验

在不同最小效用阈值下，将算法HUPN_SW与算法GHUM在数据集Retail和数据集Connect上分别进行数据准确性对比实验，结果如图11、图12所示。

图11 数据集Retail上算法的准确性

图12 数据集Connect上算法的准确性

从图11和图12可以看出：HUPN_SW算法在两个数据集的准确度分别维持在85%和90%左右，准确性在可接受范围内。原因是HUPN_SW算法基于滑动窗口实现流数据的局部挖掘而不是全局挖掘，因而挖掘结果不精确；同时，由于在数据集Connect的数据密度和平均长度都高于Retail，因此在Connect数据集上算法准确度会更高。

4 结束语

本文提出了一种基于滑动窗口含负项的高效用项集挖掘算法HUPN_SW，用于挖掘流数据上最近的高效用项集，在不产生候选效用模式集的情况下，直接挖掘出高效用模式集，避免了验证候选模式的大量资源消耗。实验结果表明了HUPN_SW算法有较高的运行效率和较好的伸缩性。该方法可以发现最近的有价值的信息，有助于用户了解客户最近的购买偏好，做出更好的经济决策。