基于RRT*改进的移动机器人路径规划算法

梁永豪，陈秋莲，王成栋

(广西大学 计算机与电子信息学院，广西 南宁 530004)

0 引 言

机器人路径规划，是通过算法在有障碍物的环境中找到一条从起点到目标点的无碰撞路径。路径规划算法作为移动机器人的关键技术之一，受到国内外学者的广泛关注。

目前，路径规划算法主要包括遗传算法[1]、粒子群算法[2]、人工势场法[3]、基于网格的算法[4]和基于采样的算法[5，6]。基于采样的算法通用性比较强，受环境维度和复杂度的约束较小[7]，是当前最流行的路径规划算法之一。快速扩展随机树(RRT)[8]是基于采样算法的典型代表，依靠随机采样和碰撞检测模块，在给定的空间内生成一组离散的点。虽然RRT可以快速找到路径，但它不能确保找到的路径是最优的。RRT*[9]是RRT算法的变体，在添加新节点时引入两个优化模块：重选父节点和重布线。优化模块确保在采样点趋于无穷时，RRT*算法找到最优解。

RRT*是RRT算法发展的一个里程碑，吸引了很多学者，主要从两个方面对算法的性能进行改进：采样策略和树扩展策略。采样策略主要是通过优化采样点，加速算法收敛。如知情采样Informed-RRT*[10]限制采样点在椭圆形采样区域内；目标偏置[11]和人工势场法[12]利用目标点的信息来指导新节点生成方向；Bi-RRT*[13]则采用双树拓展的同时引入启发式思想，加快收敛速度。树扩展策略则是对扩展树本身的结构进行优化，使路径长度尽可能短。如Quick-RRT*[14]使用三角不等式来优化重选父节点和重布线模块，缩短路径长度；F-RRT*[15]在Quick-RRT*的基础上以创造父节点替代重选父节点；KB-RRT*[16]通过添加运动学约束，减少不必要的节点生长，获取满足运动学约束，路径更短的扩展树。但这些改进依旧存在不足，如F-RRT*路径规划的效率还有不少的提升空间，同时在复杂障碍物环境下会产生较多的冗余节点；目标偏置在局部最优环境或者迷宫下，性能显著下降；人工势场法在多障碍物环境下计算量大，效率比较低。

针对RRT*中存在的盲目搜索、路径较长和冗余节点多而导致路径规划效率低，本文提出一种融合树扩展策略和采样策略的改进RRT*算法(AF-RRT*)。采样策略方面，采用动态步长，减少冗余节点；利用自适应探索，减少采样的盲目性，加快路径规划速度，同时避免陷入局部最优；树扩展策略方面，引入创造父节点，并与采样策略有效融合，减少路径长度。

1 相关工作

1.1 RRT算法

RRT的搜索过程类似于树不断地向四周扩散生长。起点xstart为扩展树G的根节点，树中节点用集合V表示，节点间的连接用集合E存储。在自由空间随机采样节点xrand引导树的生长方向。找到离随机点最近的节点xnearest，在xnearest和xrand连线上以步长eta生成新节点xnew。若最近邻节点与新节点之间的路径与障碍物无碰撞，则将新节点加入树中，否则重新采样。重复上述过程，直到新节点扩散到目标点，完成整个搜索，返回该节点到根节点的连线作为路径。伪代码如算法1所示：

Algorithm1:RRT()

Input:xstart,xgoal,Map,K,eta,

Output:G=(V,E)

(1) V ← {xstart},E ← ∅;

(2)fori=1 to Kdo

(3) xrand← SampleFree(i);

(4) xnearest← Nearest(V,xrand);

(5) xnew← NewState(xnearest,xrand,eta);

(6)ifCollisionFree(xnew,xnearest)then

(7) V ← V ∪ {xnew};

(8) E ← E ∪ {(xnearest,xnew)};

(9)ifDistance(xgoal,xnew) <λthen

(10)returnG=(V,E);

(11)endif

(12)endif

(13)endfor

其中函数SampleFree()在自由空间内生成随机节点；Nearest()利用欧式距离选择树节点中离随机节点最近的节点；NewState()从两点连线方向上扩展固定步长，得到新节点；CollisionFree()判断给定两点间的连线是否在自由空间。

1.2 RRT*算法

RRT的随机扩展性使算法稳定性差，无法收敛至全局最优。RRT*在树扩展过程中，确定随机点位置后，对新加入搜索树的新节点，增加重选父节点和重布线操作。

RRT*的伪代码如算法2所示，第(7)行和第(10)行分别为重选父节点ChooseParent()和重布线Rewire()。通过随机点的增加实现路径的渐进优化，当随机点数量趋于无穷时能够获得最优解。

Algorithm2:RRT*()

Input:xstart,xgoal,Map,K,eta,Rnear

Output:G=(V,E)

(1) V ← {xstart},E ← ∅;

(2)fori=1 to Kdo

(3) xrand← SampleFree(i);

(4) xnearest← Nearest(V,xrand);

(5) xnew← NewState(xnearest,xrand,eta);

(6)ifCollisionFree (xnew,xnearest)then

(7) xmin← ChooseParent(xnew,V,Rnear);

(8) V ← V ∪ {xnew};

(9) E ← E ∪ {(xmin,xnew)};

(10) G ← Rewire(V,E,xnew,Rnear);

(11)ifDistance(xgoal,xnew) <λthen

(12)returnG=(V,E);

(13)endif

(14)endif

(15)endfor

(1)重选父节点ChooseParent()函数：以新节点xnew为圆心，产生以Rnear为半径的邻域Xnear，以邻域内的节点为备选父节点。首先计算xnew与邻域内所有节点连接后的权值大小，若邻域内中存在节点xmin，使以xmin为父节点的xnew权值最小，则删除xnew与原父节点xnearest的边，在树中新增xnew与xmin的边集，如图1(a)所示。

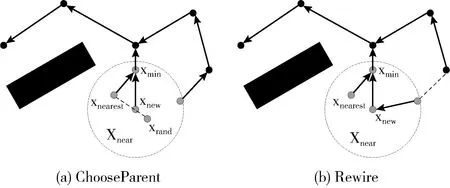
图1 RRT*的树扩展

(2)重布线Rewire()函数：重布线则是在RRT采样后加入了剪枝过程，优化新节点附近的旧节点。若邻域内存在节点的权值大于以xnew为父节点到该节点的权值，则剪掉这些节点与原父节点的连线，以xnew作为新的父节点，更新邻域内其它节点的路径长度，如图1(b)所示。

2 AF-RRT*算法

RRT*算法能渐进达到最优，但存在随机性过大、路径代价大和冗余节点等不足，计算量随节点数量的增加而急剧增加，需要较长的时间才能逼近最优解。本文提出一种融合树扩展策略和采样策略的AF-RRT*算法，提高路径规划效率。

2.1 AF-RRT*算法描述

AF-RRT*在RRT*基础上，进行3方面的改进：①动态步长，减少由于震荡现象导致的冗余节点；②自适应探索，减少采样的随机性；③创造父节点代替RRT*的重选父节点，使扩展树贴近障碍物生长，减短路径长度。伪代码如算法3所示：

Algorithm3:AF-RRT*()

Input:xstart,xgoal,Map,K,Ddich,eta,Rnear,Cnow,Ccol,Pgoal,Prand

Output:G=(V,E)

(1) V ← {xstart},E ← ∅;

(2)Fori=1 to Kdo

(3) xrand← SampleFree(i);

(4) xnearest← Nearest(V,xrand);

(5) Eta ← DSS(xnearest,xgoal,eta);

(6) xnew← AES(xrand,xgoal,xnearest,Eta,&Cnow,Ccol,Pgoal,Prand);

(7)ifxnew≠ xrandthen

(8) xreachest← FindReachest(G,xnearest,xnew,xstart);

(9) xcreate←CreateNode(G,xreachest,xnew,Ddich,xstart);

(10)ifxcreate≠ ∅then

(11) V ← V ∪ {xcreate,xnew};

(12) E←E∪{(Parent(xreachest),xcreate),(xcreate,xnew)};

(13)else

(14) V ← V ∪ {xnew};

(15) E ← E ∪ {(xreachest,xnew)};

(16)endif

(17) G ← Rewire(V,E,xnew,Rnear);

(18)ifDistance(xgoal,xnew) <λthen

(19)returnG = (V,E);

(20)endif

(21)endif

(22)endfor

其中函数DSS()根据当前最邻近节点与目标点的距离动态调整步长；AES()根据扩展树各节点位置，进行自适应探索，生成新节点；FindReachest()搜索与新节点连线不经过障碍物的最远祖先节点；CreateNode()生成创造节点，在障碍物边缘连接最远祖先节点和新节点。

算法在第(1)、第(2)行初始化扩展树，没达到最大迭代次数时，进入循环。

第(3)～第(7)行产生新节点。确定随机点xrand与最近节点xnearest后，DSS()根据xnearest与目标点的距离计算动态步长，AES()使用当前步长生成新节点xnew。

第(8)～第(16)行是创造父节点的过程，分为两步。FindReachest()找到新节点xnew的最远祖先节点xreachest。CreateNode()根据xnew和xreachest的位置，在障碍物边缘生成创造节点xcreate。若xcreate不为空，则将xnew和xcreate加入扩展树；否则将xnew加入扩展树。

第(17)～第(22)行是重布线和算法终止条件。

2.2 动态步长

RRT*算法生成新节点xnew后，判断其是否在目标点xgoal的λ邻域，若是，则找到一条可行路径。为了保证算法的效率，通常取步长为eta>λ。但是，若xnearest与xgoal的距离在(λ，eta)之间，使用固定步长进行扩展会造成目标点附近的震荡。大地图中采用大扩展步长时震荡现象尤为明显，会增加路径规划时间和冗余节点。DSS()函数通过动态步长来解决震荡问题。每次扩展，先计算xnearest和xgoal的距离Dis，若Dis>eta时，则扩展步长不变；否则，将扩展步长调整为Dis。

2.3 自适应探索

扩展树新节点的探索可以分为强探索和弱探索。强探索状态下扩展树往随机节点生长，增加多样性；弱探索状态下扩展树往目标点生长，缩短搜索时间。AES()函数可根据扩展树的探索状态生成新节点。

Function:AES()

Input:xrand,xgoal,xnearest,Eta,Cnow,Ccol,Ccont,Pgoal,Prand

Output:xnew

(1) xnew← xrand;

(2) P ← Estatus(Cnow,Ccol,Pgoal,Prand);

(3) xpnew← xnearest+P*(xgoal-xnearest)*Eta+(1-P)*(xrand-xnearest)*Eta

(4)ifCollisionFree (xnew,xnearest)then

(5) xnew← xpnew;

(6)else

(7) xpnew← xnearest+(1-P)*(xgoal-xnearest)*Eta+P*(xrand-xnearest)*Eta

(8)ifCollisionFree (xnew,xnearest)then

(9) xnew← xpnew;

(10)else

(11) Cnow← Cnow+1

(12)endif

(13)endif

(14)returnxnew

其中Estatus()为扩展树的探索状态函数。初始状态为弱探索，Cnow为扩展树新节点生成失败次数。Cnow除以Ccol取整，若为奇数，则返回值为Prand，扩展树进入强探索状态；否则，返回值为Pgoal，扩展树进入弱探索状态。Prand+Pgoal=1。调整参数Ccol，可控制扩展树探索状态切换的速度。

在确定P值后，新节点由目标点和随机点共同确定。目标点和随机点两个方向的权值分别是P和(1-P)，进行矢量合成确定新节点的扩展方向和扩展距离。

新节点坐标由式(1)确定，其中Eta为扩展步长

(1)

弱探索状态时，扩展树偏向目标点生长，如图2黑色平行四边形所示。若新节点xnew和最近点xnearest的连线不经过障碍物，则扩展成功；否则，交换随机点和目标点的权值，使树偏向随机点扩展，如图2灰色平行四边形所示。再次进行碰撞检测，若通过则扩展成功；否则失败次数加1，重新采样。通过交换目标点和随机点两个方向的权值，快速绕开障碍物。

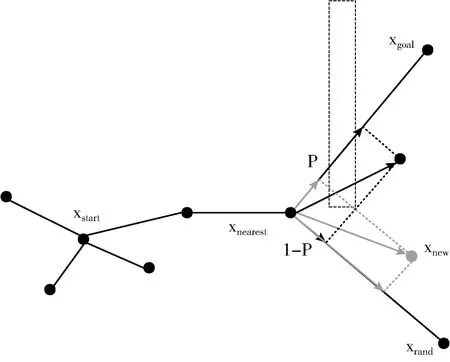
图2 新节点扩展的自适应探索

2.4 创造父节点

RRT*在现有的树节点中重选父节点，如果邻域内路径代价普遍比较大，父节点重选作用不大。增大邻域半径可以扩大父节点选择范围，但邻域内节点数量增加会显著增加计算量。本文以创造父节点代替重选父节点，在障碍物边缘创造一个节点作为新节点的父节点，使扩展树贴近障碍物生长，降低路径代价。创造父节点由两个步骤来完成：查找最远祖先节点和创造新节点。

(1)查找最远祖先节点：伪代码见函数FindReachest()。把最邻近节点赋给xreachest。判断xreachest的父节点与xnew的连线是否在自由空间，若是则把xreachest的父节点赋给xreachest，继续搜索其父节点。否则返回当前xreachest。

Function:FindReachest()

Input:G,xnew,xnearest,xstart

Output:xreachest

(1) xreachest← xnearest;

(2)Whilexreachest≠ xstartdo

(3)ifCollisionFree(xnew,Parent(xreachest))then

(4) xreachest← Parent(xreachest);

(5)else

(6)returnxreachest

(7)endif

(8)endwhile

(9)returnxreachest

由于只搜索xnew的祖先节点，不搜索xnew周围的节点，搜索节点数量大幅度减少，降低了搜索时间。

(2)创造新节点：在xreachest及其父节点之间的连线上找到节点xallow，使得xallow与xnew的连线L位于障碍物边缘。在连线L上找到一点xcreate，使xcreate可同时连接xnew和xreachest的父节点，如图3粗实线路径所示。从图3中可以明显看出粗实线路径比虚线路径短。与重选父节点的路径(图1(a))相比，路径长度更是短得多。

图3 创造父节点过程

创造新节点过程的伪代码见函数CreateNode()，第(4)～第(11)行找到节点xallow确定连线L的位置，第(13)～第(20)行找到节点xcreate。其中参数Ddich用来控制新节点与障碍物的逼近程度。Ddich越小，路径长度越短，计算时间越多。调整Ddich的大小，可以平衡路径长度和时间代价。

Function:CreateNode()

Input:G,xreachest,xnew,Ddich,xstart

Output:xcreate

(1) xallow← xreachest;

(2)ifxreachest≠ xstartthen

(3) xforbid← Parent(xreachest);

(4)WhileDistance(xallow,xforbid) >Ddichdo

(5) xmid← (xallow+xforbid)/2;

(6)ifCollisionFree(xnew,xmid)then

(7) xallow← xmid;

(8)else

(9) xforbid← xmid;

(10)endif

(11)endwhile

(12) xforbid← xnew;

(13)WhileDistance(xallow,xforbid) >Ddichdo

(14) xmid← (xallow+xforbid)/2;

(15)ifCollisionFree(Parent(xreachest),xmid)then

(16) xallow← xmid;

(17)else

(18) xforbid← xmid;

(19)endif

(20)endwhile

(21)endif

(22)ifxallow≠ xreachestthen

(23) xcreate← xmid;

(24)else

(25) xcreate← ∅;

(26)endif

(27)returnxcreate

3 实 验

仿真实验通过python实现，实验环境为：Windows10，Intel(R) Core(TM) i7-5500U，主频2.40 GHz，内存8 G。地图中S点为起点，T点为终点，黑色矩形为障碍物，白色为自由区域，黑色细线是算法在路径规划中生成的扩展树。为验证算法的有效性，在4个不同障碍物的全局环境，分别与原始算法RRT*、F-RRT*进行对比实验。地图大小均为640×480，公共参数设置：初始步长eta=40，目标点邻域λ=15，搜索半径Rnear=45，Ddich的取值为2，Ccol的取值为50，Prand取值为0.2，Pgoal取值为0.8。

3.1 仿真实验

3.1.1 简单障碍物环境

简单障碍物环境如图4所示，只有一个矩形障碍物。3种算法分别进行100次路径规划所得的平均数据，如表1所示。

表1 简单障碍物环境下的对比

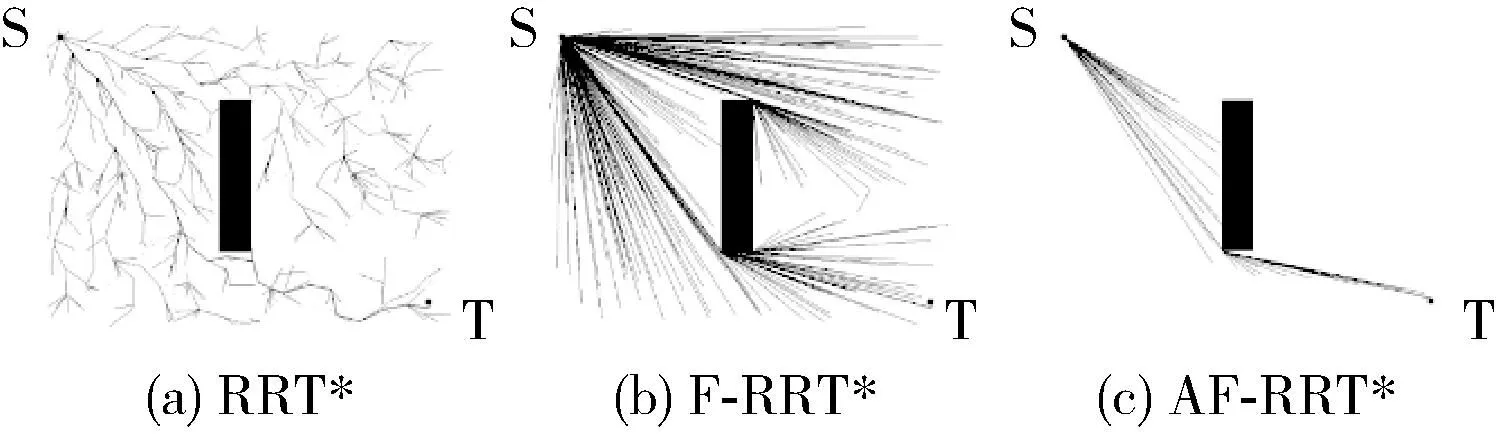
图4 简单障碍物环境的路径规划结果

在扩展节点数和路径规划时间这两个指标上，AF-RRT*明显优于RRT*和F-RRT*。AF-RRT*扩展节点数比RRT*少75.25%，路径规划时间少90.19%，路径长度短11.52%。AF-RRT*与F-RRT*的路径长度接近，但是扩展节点数减少77.43%，路径规划时间减少90.48%。

3.1.2 迷宫障碍物环境

地图上中有两个平行的矩形组成一个简单迷宫，如图5所示。3种算法100次路径规划所得的平均数据见表2。AF-RRT*的路径长度与F-RRT*算法接近，扩展节点数量和路径规划时间远少于其它两种算法。AF-RRT*相比于F-RRT*，扩展节点数减少41.30%，路径规划时间减少63.25%。

表2 迷宫障碍物环境下的对比

图5 迷宫障碍物环境的路径规划结果

3.1.3 凹形障碍物环境

地图中有一个凹形障碍物，如图6所示。3种算法100次路径规划所得的平均数据见表3。

表3 凹形障碍物环境下的对比

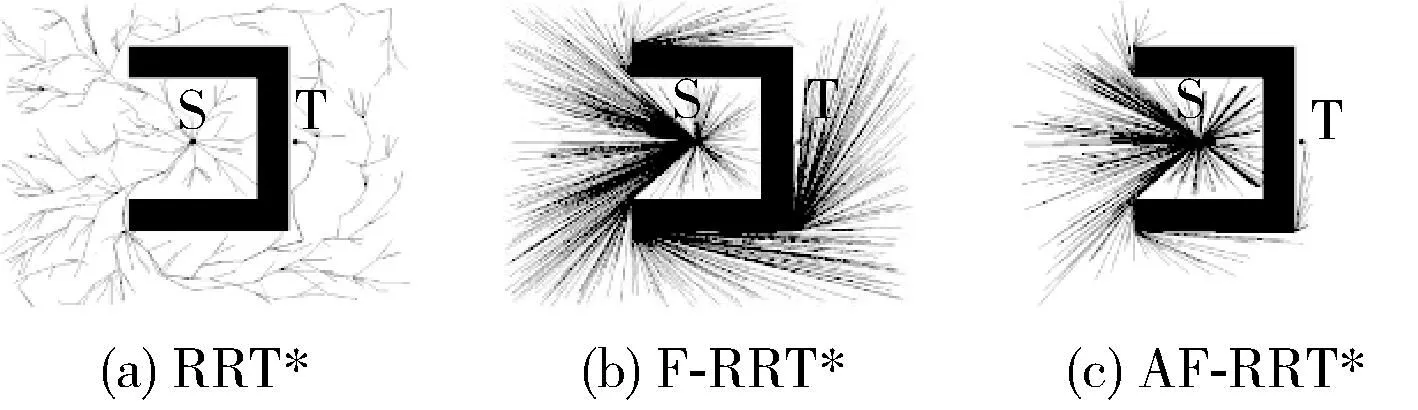
图6 凹形障碍物环境的路径规划结果

AF-RRT*相比于F-RRT*，扩展节点数减少48.43%，路径规划时间减少69.21%。

3.1.4 复杂障碍物环境仿真

地图上中有许多各种不同类型的矩形障碍物，如图7所示。

图7 复杂障碍物环境的路径规划结果

3种算法在复杂障碍物环境下分别进行100次路径规划，平均数据见表4。在扩展节点数和路径规划时间这两指标上，AF-RRT*同样明显优于RRT*和F-RRT*。与F-RRT*算法相比，AF-RRT*的扩展节点数减少72.45%，路径规划时间减少85.29%。

表4 复杂障碍物环境下的对比

3.1.5 仿真实验分析

从结果对比可以看出，F-RRT*跟RRT*算法存在着无效搜索和在目标点震荡的问题。在多障碍物环境下，由于扩展树需要频繁绕过障碍物，F-RRT*探索无效区域时在障碍物边缘大量地创造新节点，这会使扩展节点数和路径规划时间大幅度上升。本文算法AF-RRT*利用自适应探索策略和动态步长针对性减少了在盲目搜索和扩展树震荡的过程中创造的新节点，使得扩展节点数和路径规划时间大大减少。普通环境下，如简单障碍物和复杂障碍物环境，AF-RRT*的路径规划时间比F-RRT*减少80%～90%；在局部最优或者迷宫类环境下，如迷宫障碍物和凹形障碍物，AF-RRT*的路径规划时间也比F-RRT*减少60%～70%。

3.2 消融实验

为进一步检验AF-RRT*算法各组成部分的有效性，保持相同参数不变，在复杂障碍物环境对AF-RRT*算法进行消融实验，如图8所示。

图8 AF-RRT*消融实验的路径规划结果

无创造父节点、无自适应探索策略、无动态步长的AF-RRT*和完整的AF-RRT*在多障碍物环境下分别进行100次路径规划，平均数据见表5。无创造父节点树扩展策略的AF-RRT*算法路径长度较长；无自适应探索策略的AF-RRT*算法，扩展节点数较多和路径规划时间较长；无动态步长的AF-RRT*扩展节点数较多。说明创造父节点在使扩展树紧贴障碍物生长，自适应探索策略在减少盲目搜索，动态步长在减少冗余节点，是有效的。其中自适应探索策略发挥了较为关键的作用，对提高AF-RRT*算法的性能做出了较大的贡献。

表5 AF-RRT*消融实验数据

4 结束语

本文以RRT*算法为基础，在树扩展策略和采样策略两方面作了改进。引入创造父节点的树扩展策略，改变RRT*树扩展的过程，使扩展树紧贴障碍物生长，缩短了路径长度。通过自适应探索策略，缩短了路径规划的时间，同时避免陷入局部最优。通过动态步长减少了扩展树在目标点震荡。仿真实验结果表明，AF-RRT*在路径规划效率和路径质量上相较于RRT*和F-RRT*具有较明显的优越性。消融实验验证了各改进点的有效性。