轻量级卷积神经网络的硬件加速方法

吕文浩，支小莉，2+，童维勤，2

(1.上海大学 计算机工程与科学学院，上海 200444；2.上海智能计算系统工程技术研究中心 研发部，上海 200444)

0 引 言

过去几年间，卷积神经网络(convolutional neural network，CNN)的应用范围从服务器集群上的图像处理服务逐渐扩展到了对延迟更敏感的边缘端实时应用[1，2]中。为了能够适配资源受限的计算环境，轻量级CNN[2]往往会成为这类应用的最优选择。

目前，关于轻量级CNN的硬件加速方法的研究工作还比较少，大致可分为两类。一类是优化深度可分离卷积等不便于硬件部署的轻量级操作，Yifan等使用1×1卷积和移位操作代替了深度可分离卷积[3]；另一类是保留模型完整结构的同时优化计算单元的架构设计，Di等为深度可分离卷积和标准卷积设计了两个专用计算单元来提高计算效率[4]，Ming等设计了加速架构SparkNoC，将所有层以流水线的方式同步部署到现场可编程门阵列(field programmable gate array，FPGA)上[5]。

但关于轻量级CNN的硬件加速方案主要的目标依然是根据网络结构特性对硬件架构进行针对性的优化，没有很好地结合软件进行协同优化，在模型修改灵活性和模型性能改善方面尚有很大研究空间，基于软硬件协同优化思想设计的轻量级CNN的硬件加速方法研究尚不成熟。Lu等以软硬件协同优化的方法设计了FPGA加速器，将移位量化算法与FPGA相结合[6]，但是他们提出的架构是基于传统CNN模型进行设计的，对于轻量级卷积神经网络模型则无法适用。

因此，本文选择最典型的轻量级卷积神经网络MobileNetV2[7]作为目标模型，以软硬件协同优化为指导思想，针对基于轻量级卷积神经网络的FPGA加速策略展开了研究。本文的贡献主要如下：

(1)针对FPGA加速器更擅长处理移位计算的特性，提出了一种基于可微阈值的选择性移位量化方案(differentiable threhold-based selective shift quantization，DTSSQ)，通过将浮点数权重转化为一或两个2的幂次方和的形式，将全部乘法运算转化为移位运算，从而提高加速器的性能。

(2)提出了一种基于FPGA的CNN加速器架构，将MobileNetV2中所有的网络层都映射到了独立定制的硬件单元上，对缓存设计、数据存取等方面进行了针对性优化。

(3)为了最大化硬件资源利用效率，设计了一种具有更高兼容性的卷积层计算单元，统一了数据输入输出接口并且能够支持不同卷积类型的通用化部署。

1 相关技术

1.1 MobileNetV2

MobileNetV2是一种轻量级CNN模型，主要使用了深度可分离卷积来构建网络架构，在图像分类和目标检测领域有着很显著的优势。

MobileNetV2建立在MobilenetV1的基础上，与后者相比，前者的top-1准确率从70.6%提高到了72%，模型大小也从4.2 M缩小到了3.4 M。MobileNetV2最大的特点是使用了倒置残差结构。该结构包括一个1×1的扩展层、一个3×3的逐通道卷积，和一个1×1投影层。当逐通道卷积的步长为2时，将输入与输出逐元素相加。当步长为1时则不做额外处理。

1.2 Intel FPGA SDK For OpenCL

在传统的开发方式中，FPGA是通过硬件描述语言(hardware description language，HDL)进行编程的，开发人员不仅需要掌握HDL语言，还需要熟知FPGA的硬件架构。同时由于HDL语言直接面向硬件，抽象层次较低，这严重提高了FPGA开发的准入门槛。

开放式计算语言(open computing language，OpenCL)是一门基于C/C++的语言，能够进行跨平台的并行编程，并且能够兼容各类硬件设备。而Intel FPGA SDK for OpenCL是Intel公司提供的一个OpenCL设计套件，它使用自定义的编译器将OpenCL代码映射到FPGA上，在隐藏FPGA细节的同时实现了工作优化。

这种开发方法可以极大地减少硬件开发时间，提高FPGA的开发效率。同时，基于OpenCL开发的程序也有助于复杂程序在FPGA上的快速部署。因此，本文使用OpenCL作为开发语言，完成了FPGA加速器的部署实现。

2 模型量化

2.1 量化方案

为了降低网络模型在FPGA上的存储成本和计算成本，本文使用移位量化的方案将浮点参数转化为低精度数。与移位量化不同，定点量化依然使用乘法操作来进行卷积运算，这在FPGA中通常由DSP来实现。但是与FPGA中数量较多的查找表和寄存器相比，FPGA中DSP的数量较少，往往需要对其进行特殊处理，才可能支持CNN的大规模乘法运算。因此DSP资源的数量通常是限制加速器性能的重要原因。

而移位操作在FPGA中通常由查找表来实现，几乎不会消耗DSP资源，因此FPGA加速器的性能将不会受到DSP资源的限制，并减少因过度使用DSP而产生的功耗[8]。但如式(2)所示，由于移位量化的每个量化值都是2的幂次方，当量化值的目标位宽b增加时，量化值集合Qshift内包含的值只会在0附近增加[2-2b+1，2-2b-1]区间内的有限个值，而其它区间不会发生任何变化，这种分布上的不均匀使得模型的量化性能无法被有效地提升

Qshift={0，±2-2b-1+1，±2-2b-1+2，…，±2-1，±1}

(1)

为解决这个问题并增加权重表示的灵活性，本文提出了一种基于可微阈值的选择性移位量化方案。该方案使用一或两个2的幂次方来表示权重，对量化值进行了更细粒度的划分。

量化函数定义如下

(2)

(3)

(4)

其中，b表示权重量化的位宽，W(i) 表示第i层的权重数据，P表示权重的移位值，Wq(i) 表示第i层权重的量化表示形式，clip(.)表示裁剪函数。在式(4)表示的量化函数的作用下，形如0.128这样的全精度权重最终会被表示为2-3的形式。

2.2 基于可微阈值的权重分组

相比于将权重直接量化为两个2的幂次方的和，如果将一部分权重量化为两项之和并且将另一部分权重量化为单个项，则能够保持高分辨率带来的高精度优势，同时也具有移位量化带来的低能耗优势。

基于这一假设，本文提出的DTSSQ方案包括下列步骤：基于可微阈值的权重分组和重训练。

基于阈值的权重分组根据量化误差将权重划分为3组，分别对应权重被量化为两项之和、被量化为单项和不被量化。第一组的权重经过两次移位量化，以减小量化误差。第二组的权重仅需要经过一次量化，即可逼近全精度的权重值。第三组的权重在前向传播的过程中将不会进行移位量化，其值是由量化函数计算得到的零值。

本文将R(i) 定义为第i层权重的量化误差，则R(i) 可以通过式(5)来表示

R(i)=W(i)-Quant(W(i))

(5)

如果权重的量化误差大于阈值，权重就会被划分到第一组，反之则被划分到第二组。这种动态的分组模式在数学中可以通过二值掩码矩阵来表示，具体表示见式(6)

(6)

式中：T为判断量化误差与阈值大小关系的二值掩码矩阵，t表示量化误差的阈值。因此，使用该方案计算得到的量化后的权重值就可以通过式(7)进行表示

Wq(i)=Quant(W(i))+Quant(R(i)⊙T)

(7)

式中：⊙表示逐元素相乘。根据T的不同取值，Wq(i) 可能会被表示为一或两个移位值和的形式，也就是形如0.128这样的全精度权重最终可能会被表示为2-3+2-5或者2-3的形式。完整的权重分组方案如算法1所示。

算法1：基于阈值的权重分组方案

输入：全精度权重w

阈值t

输出：量化后的权重w_q

(1)计算全精度权重的单项量化值w1：w1=Quant(w)

(2)根据w1计算权重的量化误差error：error=w-w1

(3)if error >=tdo

(4)w_q= w1+Quant(error)

(5)else

(6)w_q=w1

(7)end if

(8)returnw_q

在实践中，该类阈值如果被设置为静态值，将无法反映量化过程中权重的变化和迭代过程中量化误差的变化，因此，本文将引入可微阈值t作为权重划分的依据，并通过重训练求解出阈值的最优解。

2.3 重训练

为了更好地减少重训练时的量化误差，并使权重在反向传播过程中更逼近2的幂次方，本文提出了一个正则化项Ω来辅助权重的修正

(8)

因此，与新的正则化项Ω结合之后，新的损失函数将变化为如下形式

lossnew=loss+λ*Ω

(9)

式中：λ是预定义的一个超参数。

根据反向传播的链式求导法则，损失函数对权重的偏导数可以由下列公式计算得出

(10)

但是Wq(i) 的计算涉及了对全精度权重的四舍五入的运算，这使得∂Wq/∂W的导数处处为0(除了W恰好为2的幂次方的离散点)，权重的梯度无法正常进行反向传播。以前的一些工作[9，10]大多通过令∂Wq/∂W=1来直接获取梯度的近似值，虽然看似解决了问题，但是却完全忽略了量化对权重造成的影响，当进行低比特的量化时，量化误差会被放大，导致训练过程难以收敛[11]。

本文引用了Junghyup等[12]提出的EWGS方法来尝试解决这一问题。根据文献[12]可以计算出损失函数对权重的偏导数∂L/∂W，如式(11)所示

(11)

式中：δ是一个大于等于0的比例因子。

根据式(7)，阈值t的梯度可以通过Wq(i) 进行计算，具体计算公式见式(12)

(12)

在计算∂Wq/∂t这一项时，可以使用tanh函数进行近似计算。令∂T/∂t=tanh(R(i)2-t)，则求值的具体公式见式(13)

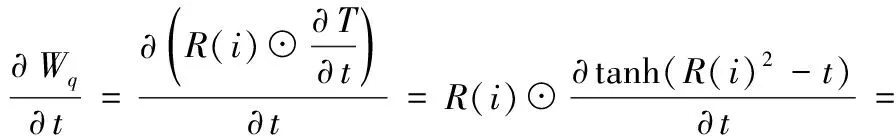
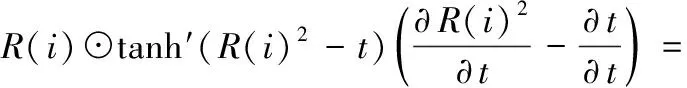
-R(i)⊙tanh′(R(i)2-t)

(13)

3 加速器设计

FPGA加速器整体架构如图1所示，包括控制器、卷积层计算单元、片上缓冲区、外部存储器和其它层的计算单元。

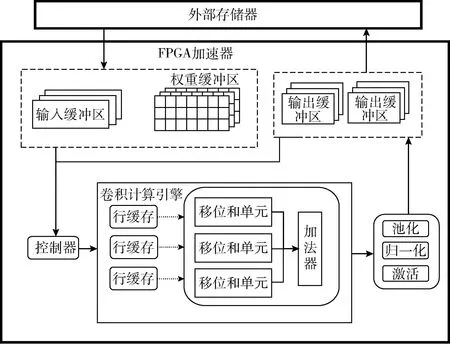
图1 加速器架构

控制器负责协调不同计算单元在运行期间的执行顺序，驱动加速器以流水线模式高效运行。卷积层的计算单元主要负责MobileNetV2中不同卷积模块的计算，最多可兼容标准卷积、逐通道卷积以及逐点卷积等3种不同卷积模块的实现。外部存储器主要用于存储原始输入图像和最终计算结果，仅在网络输入和输出端与片上产生交互。片内缓冲区包括输入缓冲区、输出缓冲区和权重缓冲区等，遵循了分层存储策略，根据参数的数量和使用频率来分配各自的片上存储资源。其它层的计算单元主要包括了MobileNetV2中涉及的全局平均池化层、Relu6激活函数层以及BN层等。

3.1 数据流

加速器包含控制器、卷积模块、池化层、BN层、激活等多个FPGA内核。内核之间的数据流动效率将直接影响加速器的推理速度。OpenCL SDK提供了通道作为内核之间通信的桥梁，这意味着内核之间可以使用先进先出(first in first out，FIFO)缓冲区直接进行片上通信。如图2所示，加速器的数据流就是使用通道按照顺序构建起来的。

图2 数据流

加速器上的数据流动，可以分为阻塞式和非阻塞式。当加速器开始运行时，控制器处于阻塞式读取模式，此时控制器要确保读取的数据可用，以便整个流水线可以正确启动。输入图像和权重数据从片外内存加载到片上缓冲区中，当控制器读取到数据时，开始执行卷积、激活、池化的计算流程。池化单元计算得到的输出值被写回控制器，此时加速器开始执行层间计算流程，并且控制器将切换为非阻塞式读取模式以避免加速器在运行期间因阻塞而停止运行。同时如果该层存在残差连接，则将输出结果提前写入到输出缓冲区内。

3.2 内存布局

一般来说，与片外内存的频繁通信会导致加速器能耗增加，因此本文使用了片上缓存来存储网络中间层的全部输出数据以减少与片外的通信。类似的研究中大多使用双缓冲区技术也就是使用两个相同的缓冲区在每个时钟周期内同时读写来加速数据处理过程。然而，这种技术的主要缺陷在于双缓冲区的尺寸需要满足中间层的最大存储需求。因此，本文提出了非对称式动态双缓冲区技术，将内存区域划分为两块大小不等的子区域，并根据实际网络模型的架构设置不同的缓冲区配置比例。因此，缓冲区的大小的计算实际上就可以被转化为求解以下问题

argmin(SIZE(layeri)+SIZE(layeri+1))

(14)

根据求解得到的结果，就可以得到最优的缓冲区配置比例。并且将最优比例与每一层的中间数据大小相结合，就能够提前计算出每一层的缓冲区读取基地址和缓冲区写入基地址。控制器通过指令流将预计算的基地址传入加速器，从而实现运行时对缓冲区的动态数据读写。经计算，在MobileNetV2层中的最优缓冲区配置为第五层与第六层的组合。

3.3 卷积计算单元

深度可分离卷积比普通卷积有更低的参数量和计算成本，但它也给基于标准卷积的加速体系结构带来了相当大的挑战[13]。适用于标准卷积的计算单元，往往无法在逐通道卷积和逐点卷积的运算模式中高效地运算。

Ming等[5]尝试为每种卷积运算类型设计一个专用引擎来针对性地提高计算效率，但是在MobilenetV2中3种卷积类型各自的计算量很不平衡，反而会使得不同计算单元的工作负载不平衡，进而导致整体硬件资源利用率降低，白白浪费功耗。相反，如果为不同的卷积类型设计一个统一的计算单元，就可以解决负载不平衡的问题，获得更高的计算资源综合利用率。

本文将卷积计算单元从逻辑上分解为移位计算阵列和加法器树，并根据不同的卷积类型设计了不同的组合方案，从而提出了一种可兼容多个卷积类型的新的计算单元设计方案。为了保证计算单元在不同工作模式下保持统一，本文针对不同卷积类型设计了专门的数据重排序过程。同时，本文根据标准卷积、逐通道卷积、逐点卷积等卷积类型的不同计算策略提出了能够在统一的硬件电路上部署的并行化策略。

如图3所示，一个完整的卷积计算单元包含了行缓冲区以及移位和阵列。

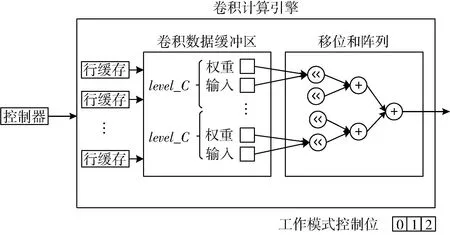
图3 卷积计算单元架构

在卷积计算之前，控制器将下一层的输入数据和权重参数进行分组并分别发送给卷积计算单元。引擎的行缓存按照非对称式动态双缓冲区的设计思路接收并存储这些数据，同时也将当前层计算所需的数据发送到移位和阵列。根据预先配置的工作模式控制位，移位单元阵列和加法器树会以不同的方案进行配置。移位单元阵列利用FPGA中数量充足的查找表对数据实现移位运算，最后再由加法器树对中间结果求和从而完成整个卷积计算。

3.3.1 标准卷积

为了充分利用FPGA设备的硬件资源，提高标准卷积模式下的并行性，本文针对参与运算的数据设计了5个并行级别，并将其定义为计算单元并行度level_R，输出通道并行度level_N，输入通道并行度level_C，宽度并行度le-vel_W，高度并行度level_H。同时，将level_R的值设置成输出通道并行度level_N，以确保运算单元能正确处理输入数据的格式，使每一个计算单元最终只生成一个通道的输出数据。

为了更好地描述计算单元在特定模式下的并行计算能力，本文将Parallelstandard定义为在指定工作模式下，计算单元在一个时钟周期内并行执行的卷积运算次数。因此标准卷积模式下的计算单元并行度Parallelstandard可以通过下列公式计算

Parallelstandard=k×level_R×(level_W-k+1)×

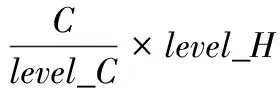
(15)

式中：k表示卷积核的尺寸，C表示输入特征图的通道数。

如图4所示，为了使不同工作模式下的数据格式保持一致并与并行策略相匹配，输入数据会被重新排序。

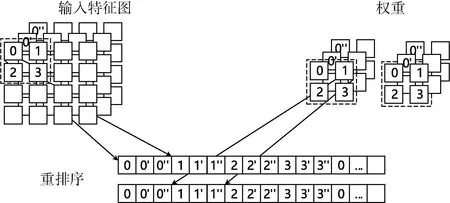
图4 标准卷积工作模式的数据重排序

图的顶部为输入特征图阵列和权重阵列，底部为重排序后的数据存储格式。顶部的序号表示输入数据在滑动窗口内的原始存储顺序，经过重新排序后与底部的序号形成一一对应关系。最终，计算单元会根据图中的数据存储格式接收输入数据和权重数据，并最终计算出卷积结果。

3.3.2 逐点卷积

逐点卷积的计算过程实际上等同于1×1卷积，之前的工作[4，6，13]中使用标准卷积的计算单元直接实现逐点卷积而没有进行专门的优化。然而，由式(16)所示，这种方式实际上会使得当前计算单元的并行度Parallelpointwise降低约level_H倍，没有充分利用计算标准卷积所需的硬件资源

(16)

因此，逐点卷积也需要对数据的读取顺序进行如图5所示的重排序过程。逐点卷积工作模式下，计算单元将会按顺序依次读取3个输入通道的权重，并重排序组合成与标准卷积一致的数据排列顺序。

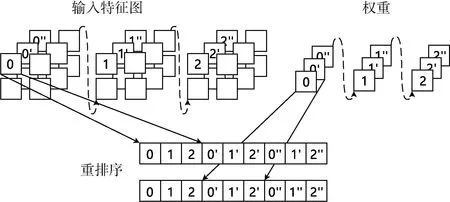
图5 逐点卷积工作模式的数据重排序

权重数据的重排序将使得计算单元在逐点卷积的模式下能够保持与在标准卷积模式时一致的数据排列顺序，因此计算单元即使处于逐点卷积模式，也可以充分利用标准卷积时用到的移位单元阵列和加法器树模块。

3.3.3 逐通道卷积

与标准卷积相比，逐通道卷积在计算过程中最大的不同是每个输出特征图通道都是由一个内核通道与一个输入特征图通道进行卷积而产生的，并且每个维度之间均没有数据依赖关系。

因此逐通道卷积的并行计算能力Paralleldepthwise实际上降低了level_R倍，这意味着同一时间只有一个计算单元在进行运算，完全丧失了level_R并行度的优势。因此，本文利用了逐通道卷积的计算特性，通过控制器对输入数据进行如图6所示的重排序，使得输入数据以额外的level_R维度被送入，从而充分能够利用多个计算单元并行处理的优势。

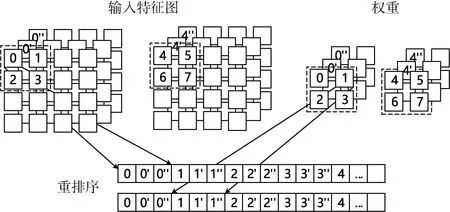
图6 逐通道卷积工作模式的数据重排序

图7显示了优化后的计算单元在处于逐通道卷积工作模式下会被激活的计算阵列，其中实线部分表示被激活的阵列而虚线部分则表示未被激活的部分。不同工作模式仅在加法器树的连接配置中有所区分。

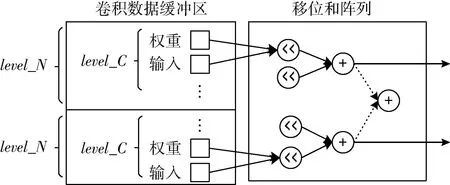
图7 逐通道卷积的计算阵列

最终，优化后的Paralleldepthwise可以通过式(17)计算得出

Paralleldepthwise=

k×level_R×(level_W-k+1)×level_H

(17)

4 实验结果

4.1 量化方案

为了评估本文提出的DTSSQ量化方案的有效性，本文使用CIFAR-10和CIFAR-100数据集对模型进行训练，这两个数据集是深度学习中常用的识别常见物体的数据集，分别包含了10类和100类输入图像，共计60 000张图片。

实验选取的模型为Resnet18和Resnet20，模型的编译语言为Python3.7，开发框架为PyTorch1.7.1。

本文将DTSSQ方案和在ResNet网络上表现良好的几种量化方案在CIFAR-10和CIFAR-100数据集上分别进行了比较，其中包括Zhou等[15]的DOREFA-NET、Choi等[16]的PACT、Ding等[17，18]的FlightNNs和LightNN。为与其它量化方案的实验配置保持一致，模型的第一层和最后一层不进行量化。

实验结果见表1，DTSSQ量化方案在CIFAR100和CIFAR10数据集上均表现良好，在CIFAR10数据集上Resnet20的准确率达到了92.84%，与全精度baseline相比提高了约0.8%。而在CIFAR100数据集上训练的Resnet18的准确率达到了71.84%，与baseline相比提高了约1%，与FlightNNs相比提高了约1.3%，可见基于可微阈值的方案能够有效地降低量化误差，并且通过重训练对阈值的动态调整，最终得到的量化精度与全精度网络相比也有明显提高。

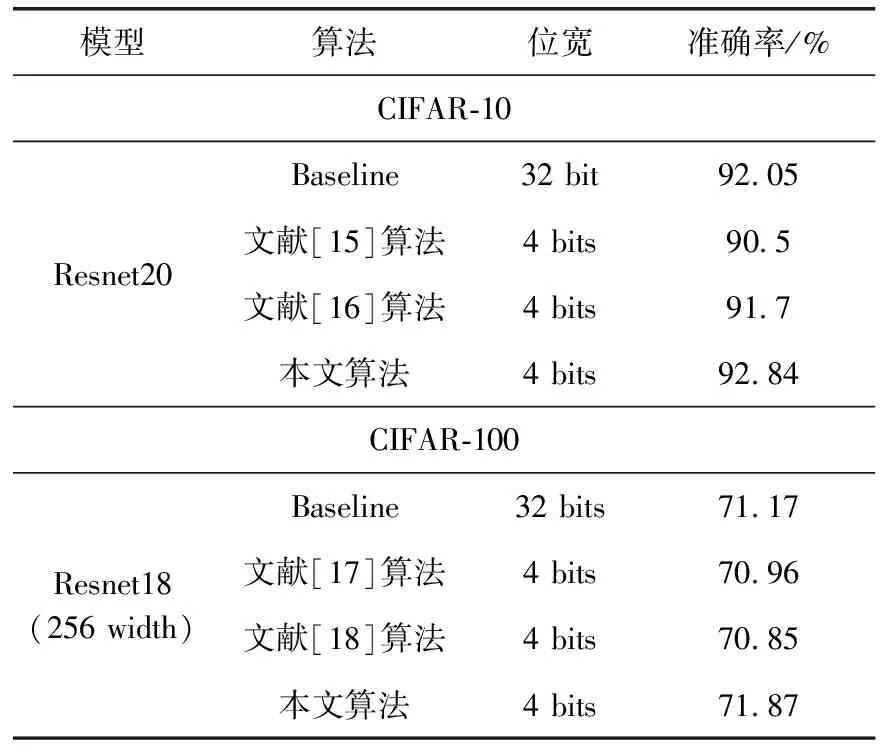
表1 量化性能结果

4.2 FPGA加速器

轻量级卷积神经网络硬件加速器部署的平台为Intel Arria10 GX1150，软件开发环境为CentOS Linux release 7.9.2009+Intel OpenCL 19.1 SDK。使用OpenCL语言将经过软硬件协同优化后的加速器架构进行编码表达，编码完成后连接FPGA加速卡进行编译，SDK会将高层次的开发语言转化为对硬件电路的描述，最终部署完成后，整体的资源利用率见表2。

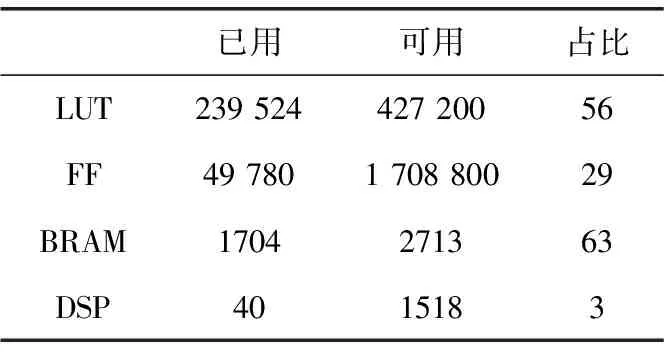
表2 资源利用率/%

本文将MobileNetV2的FPGA加速器与其GPU版本和CPU版本进行了对比实验。实验采用的CPU是12核心24线程的Intel Xeon CPU E5-2678 v3@2.5 GHZ，GPU是来自NVIDIA的专业计算卡Tesla V100。对比结果见表3。

表3 与CPU和GPU对比

从表中可以看出，CPU版本MobileNetV2的平均推理速度为29.9 ms，与之相比，FPGA加速器的平均加速比为9.3，具有更好的性能优势。而GPU作为一个通用加速器，MobileNetV2模型无法完全利用其硬件资源。因此，GPU的平均推理速度需要7.55 ms，与之对比，在FPGA上部署的模型推理速度比GPU的快了约3倍。

如表4所示，本文选取了几项类似的基于FPGA的MobileNetV2加速器实现方案，与本文设计的加速器进行了对比。

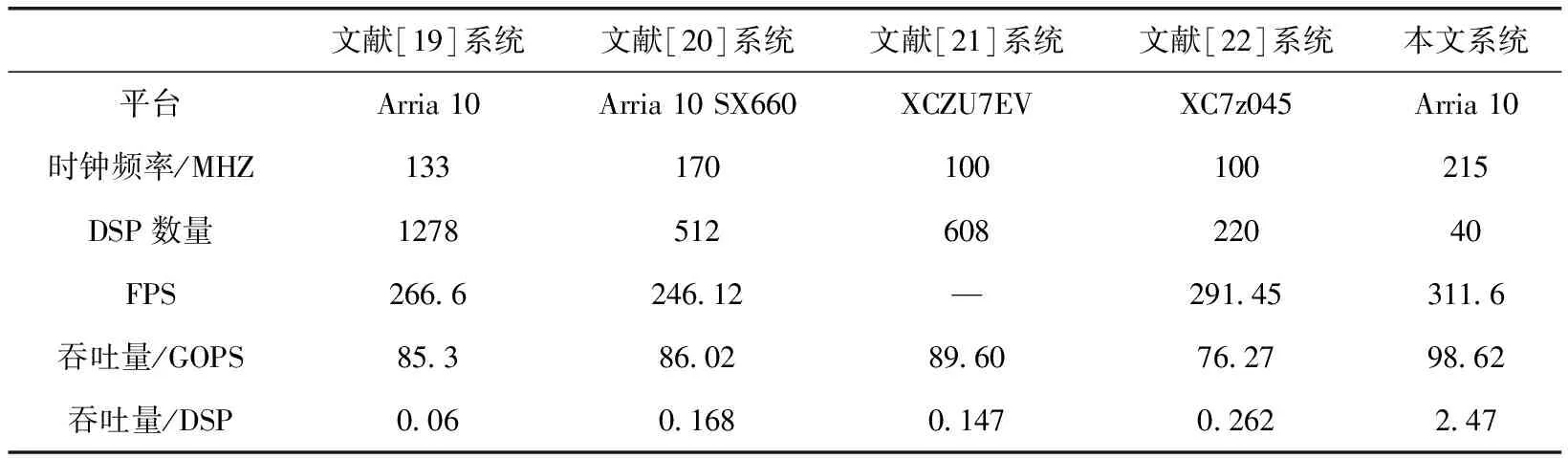
表4 加速性能对比

从表中可以看出，本文提出的加速器最终实现了311.6 fps的推理速度，优于大部分的FPGA加速器，并且本文设计的DTSSQ量化方案使得卷积的计算能够借由FPGA上充足的查找表来实现，每个时钟周期内能够完成更多的计算，因此在吞吐量方面加速器也占据了优势。

另外，本文的加速器也具备使用高级语言开发易于部署的优势。实验结果表明，我们实现的基于FPGA的轻量级卷积神经网络加速器相比其它轻量级卷积神经网络加速器实现了更高的吞吐量和更快的推理速度。

5 结束语

本文利用FPGA的硬件可编程优势，进行软硬件协同优化，对基于FPGA的轻量级卷积神经网络加速方案进行了深入研究，为进一步改善轻量化网络应用的性能提供了方法和方案。

首先，本文提出了一种基于可微阈值的选择性移位量化方案，解决了传统移位量化算法精度迅速饱和的问题。实验结果表明，提出的量化方案在CIFAR10和CIFAR100数据集上量化后的精度相比全精度网络分别提高了0.8%和1%。

其次，本文设计了一种基于FPGA的高性能加速架构来适应轻量化网络计算特征，并提出了非对称式动态双缓冲区技术与具有更高兼容性的统一卷积计算单元。实验结果表明，提出的加速器架构几乎不使用DSP就可以完成卷积运算，最终实现了98.62 GOPS的吞吐量和311.6 fps的推理速度。