化无形为有形 促进深度理解*

⦿ 江苏省南京市金陵汇文学校 田 禹

众所周知,数学知识具有高度的抽象性、概括性,若教学中仅通过讲授的方式来呈现这些内容,学生对知识的理解可能一知半解,不仅影响知识的灵活应用,而且容易滋生学生的畏难情绪,影响课堂教学效果.这些看似抽象的数学知识源于生活,是可以被观察、被感知的,并不是那么“高不可攀”.不过,根据调研发现,学生在学习几何知识时容易将其与图形建立联系,但是在解决代数问题时,常常与形割裂开来,难以体现数学的形象化和真实性,使得学习中出现漏缺,影响知识的理解深度.为了改变这一局面,教师应重视将代数知识图形化,借助图形的直观帮助学生架设抽象与现实的桥梁,让学生深度理解知识,提高教学有效性.笔者就如何搭建几何直观谈几点自己的看法,若有不足,请批评指正!

1 数学概念直观化

数学概念是构建知识体系的核心要素,是学生学好数学的关键.而数学概念是对数学对象的本质特征的高度概括,具有高度的抽象性和概括性.为了让学生深刻理解这些抽象知识,教师不妨将其与几何意义或代数意义相结合,让学生在具体情境中主动地抽象与概括,以此深刻理解知识.

在概念教学中,大多教师为了让学生能够理解概念,会通过口头表述的方式帮助学生理解和记忆,这样虽然表面上能够加速学生理解概念的进程,但是无疑会让学生产生一定的依赖,不利于学生自主学习能力的提升.同时,口头表述可能难以让学生形成深刻的印象,这样随着时间的推移,学生很容易产生遗忘,影响后期的学习效果.在概念教学中,教师若能用图形语言进行进一步的诠释,让学生多层级地理解数学概念,定能达到事半功倍的效果.

案例1绝对值的概念

在绝对值的概念教学中,大多教师会直接给出概念,然后给出具体练习让学生模仿,这样学生虽然能够正确地解答问题,但是很难深入理解概念.基于此,教师在引入概念前,利用贴近学生生活的情境,将抽象的概念与现实生活建立联系,帮助学生理解概念.情境如下:

周末,妈妈让小明和小华分别去水果店和超市买东西,去水果店需要向东走200 m,去超市需要向西走200 m,按照约定,小明去水果店,小华去超市,买到东西后原路返回.规定向东为正,向西为负,小明和小华从家出发,到达目的地的距离可以怎么表示?从目的地到家的距离又该如何表示呢?为了解决这一问题,教师鼓励学生在数轴上画一画,并让学生思考这样两个问题:(1)200和-200是一对相反数,它们到原点的距离存在怎样的关系?(2)你是如何理解负数对应的点到原点的距离的?这样通过观察、讨论,可以顺势引入绝对值的概念.

这样以生活情境为依托,借助数轴的直观,让学生对绝对值的概念有直观化理解,可以进步促进概念的深化.

2 数学公式直观化

初中阶段,学生会学习许多数学公式,它是我们解决数学问题的重要依据,是构建数学知识体系的基本要素.从传统教学习惯和学习习惯来看,大多师生不重视公式的形成过程和蕴含其中的思想方法,片面认为公式能默写会应用就可以了.殊不知,若想真正理解和掌握公式,还应引导学生从不同视角构建对公式的多元化认知,让学生通过多角度探究获得深度理解,这是学生灵活应用公式解决现实问题的必经之路.对于一些和代数相关的公式证明,教师不妨引导学生从图形的角度去诠释,这样不仅便于学生理解和掌握,而且可以降低逻辑推理的难度,为逻辑推理能力较弱的学生提供有效的学习途径,促进学生学习能力的提升.

案例2平方差公式

在“平方差公式”教学中,大多教师经常引导学生利用多项式乘多项式的方法进行推导,因为该方法是学生易于理解和掌握的,但是若教学中仅局限于一种方法,会使学生对公式的理解比较狭窄,影响学习效果.基于此,为了让学生对公式获得多维度的认知,教师可以结合图形进行直观呈现,从而让学生更好地理解数学、应用数学.

教学中,教师设计了这样一个动手拼的活动:首先让学生先剪一个大正方形纸片,然后在大的正方形纸片上剪下一个小的正方形(如图1),让学生思考剩余图形的面积.学生结合图形及正方形和长方形的面积计算公式易于给出如下推导过程:a2-b2=a(a-b)+b(a-b)=(a+b)(a-b).当然,剪拼的方式有多种,教师还可以预留时间让学生通过不同的剪拼方式来推导平方差公式.不过选择的剪拼方式不同,对思维的难度要求也不同,教师可以结合教学实际进行适度引导,以此帮助学生积累丰富的图形直观经验,提高学生实践能力.

图1

这样借助直观图形进行公式的推导,使代数公式变得更加形象化、直观化,在深化公式理解的同时,让学生感受代数与几何的内在统一,有利于培养学生的数形结合意识.

3 数学法则直观化

数学法则有许多,它是我们用数学的重要依据.对于这些法则,只有获得正确的、全面的、深刻的理解,才能使其成为我们解决生活实际问题的重要工具.在数学教学中,教师可以尝试引导学生从不同途径进行阐释,自主感悟蕴含其中的规律,实现知识的内化.例如,教师可以引导学生借助图形来解释规则,借助图形的直观让学生较为清晰地辨别法则的语义特征,通过具体到抽象再到具体的过程,让学生的思维逐渐由感性认知上升至理性认知,提升学生数学素养.

案例3多项式乘多项式的法则

在该法则教学中,教师给出图2让学生观察,然后让学生思考“如何求大长方形的面积?”学生独立解答,教师巡视,然后对学生的解题方法进行总结归纳.方法如下:

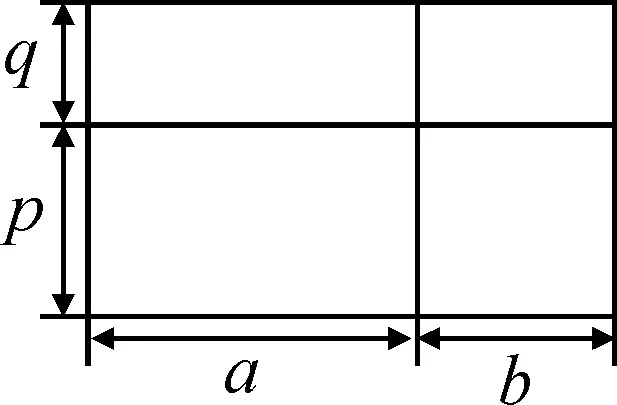
图2

方法一:直接应用长方形的面积计算公式,可得S=(a+b)(p+q).

方法二:将大长方形看成由4个小长方形拼接而成,所以有S=ap+aq+bp+bq.

方法三:将大长方形看成由2个横向的长方形拼接而成,所以有S=p(a+b)+q(a+b).

方法四:将大长方形看成由2个纵向的长方形拼接而成,所以有S=a(p+q)+b(p+q).

大长方形面积的计算方法虽然不同,但是其结果是相同的,这样根据面积不变性,即可得到多项式乘多项式的法则.

在数学法则的教学中,要善于将图形和法则联系起来,借助数的严谨性和形的直观性让学生深刻理解法则,提升教学有效性.

4 数学运算直观化

数学运算隶属程序性知识,一般情况下,学生只要按照程序化操作就能得到预期结果.不过,若教学中仅让学生按部就班地机械操作,很容易固化学生的思维,这样学生在面对一些常规方法难以解决的问题时,往往会不知所措.在面对那些无法应用常规方法解决的问题时,教师应引导学生转换思维,换个角度去思考,寻找合适的解决策略.为了帮助学生完成复杂运算,教师可以利用图形将原本零散的知识建立联系,从而找到解决问题的新思路.

该案例是一个分式运算,若利用常规方法,通过通分的方式来求解,显然运算过程是非常烦琐的.基于此,教师不妨引导学生将面积为“1”的图形进行分割,从而将问题转化为图形面积的累加问题.在该思想方法的引导下,学生可以借助圆进行辅助计算.

图3

案例4是一道需要进行简便运算的计算题,当学生利用“通法”难以解决问题时,教师引导学生利用图形进行辅助计算,以此高效地解决了问题,开阔了学生的视野.

总之,若想对知识达成深层次的理解,单凭讲授是难以达成的,教师应引导学生对相关知识进行多角度思考,帮助学生跳出习惯性思维的束缚,让学生达成持久性的理解,以此提升课堂教学品质,提升学生数学素养.