灵活运用“截长补短”法求证线段的和差关系——一道中考题的多种解法及策略分析

⦿ 黑龙江省集贤县第七中学 周 影

“截长补短”法是求证线段的和差数量关系常用的一种方法.其中,辅助线的添加是关键.“截长”是指把一条长线段按照所需截成两条较短线段,“补短”是把两条不在同一直线上的线段通过延长一条较短线段的方式把两条线段转化到一条直线上,同时又在图中构造了全等三角形、等腰三角形等.一般通过“截长”或“补短”得到的辅助线都会有一箭双雕的效果.“截长补短”的方法渗透了转化思想,有助于学生推理能力和几何直观等核心素养的培养.笔者以一道中考题为例详细解析运用“截长补短”法解决问题的策略,不当之处,还请批评指正.

1 试题呈现

(2022年黑龙江省龙东地区中考第26题)△ABC和△ADE都是等边三角形.

(1)将△ADE绕点A旋转到图1-1的位置时,连接BD,CE并延长相交于点P(点P与点A重合),有PA+PB=PC(或PA+PC=PB)成立(不需证明);

图1-1

(2)将△ADE绕点A旋转到图1-2的位置时,连接BD,CE相交于点P,连接PA,猜想线段PA,PB,PC之间有怎样的数量关系?并加以证明.

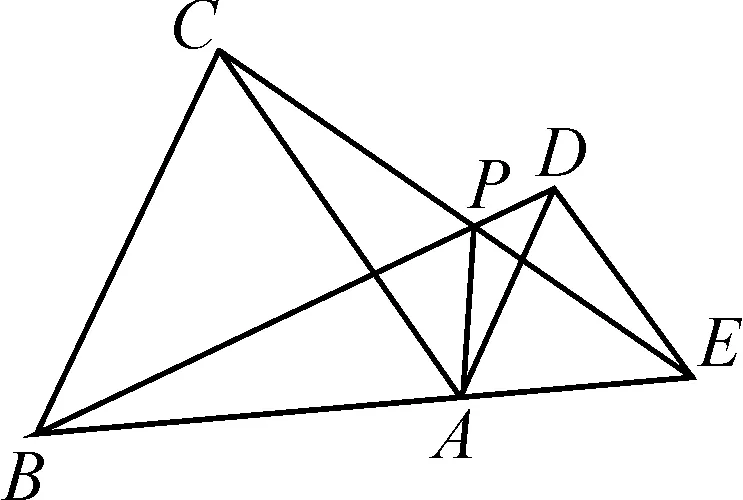
图1-2

(3)将△ADE绕点A旋转到图1-3的位置时,连接BD,CE相交于点P,连接PA,猜想线段PA,PB,PC之间有怎样的数量关系?直接写出结论,不需要证明.

图1-3

2 第(2)问的解题策略

这里只对第(2)问进行求解,具体策略如下:

“截长补短”法在证明线段的数量关系时,体现的是两种思路.如欲证a=b+c,截长法是在较长的线段a上取点M,把线段a分成线段d与线段e,取点M时,使d=b,再证e=c即可,如图2所示.补短法,则是通过把其中一条较短线段延长,使延长部分等于另外一条较短线段或者使线段延长后,等于较长的线段.如欲证a=b+c,可以把线段b延长,使延长的线段d=c,这样就把线段b和c转化到同一条线段上,证明线段b+d=a即可.或者延长线段b,使延长后的线段b+d=a,证明延长的线段d=c即可,如图3所示.

图2

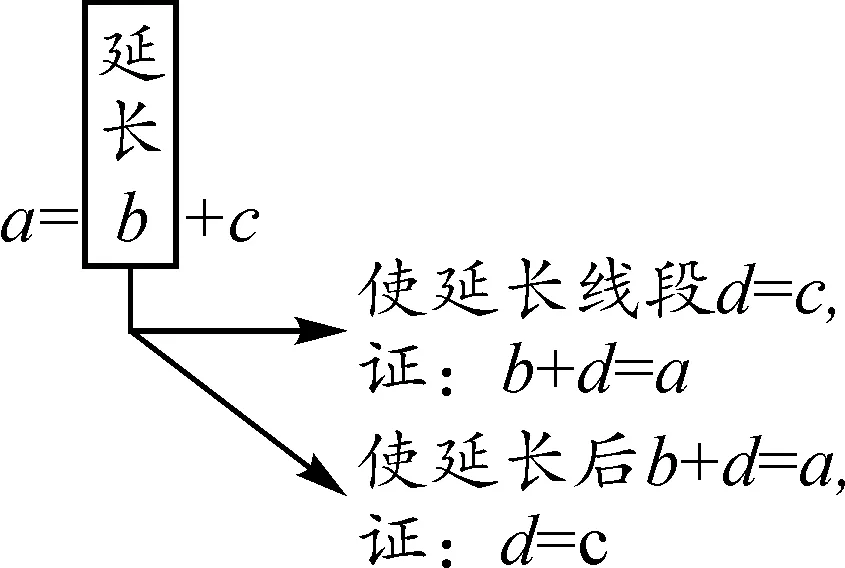
图3

3 试题解析

第(2)问的结论为PA+PC=PB;给出7种证法.

3.1 截长法

以图1-2的证明为例,截长法的证明过程如下.

证法1：如图4,在PB上截取BM=PC,连接AM.

图4

在等边三角形ABC和等边三角形ADE中,有AB=AC,AD=AE,∠BAC=∠DAE=60°.

易证∠BAD=∠CAE,所以△BAD≌△CAE,则∠1=∠2.又BM=CP,则△BAM≌△CAP,得AM=AP,∠BAM=∠CAP.于是∠BAM+∠MAC=∠CAP+∠MAC,即∠BAC=∠MAP=60°,则△MAP是等边三角形.所以PA=MP.故PB=PM+BM=PA+PC.

此种方法根据题中的已知条件和要证的结论,通过截取相等的线段构造全等三角形.如果在截取时使PM=PA,先证明△AMP是等边三角形,再证明全等三角形也可以.详细证法如下:

证法2：如图5,在PB上截取PM=PA,连接AM.

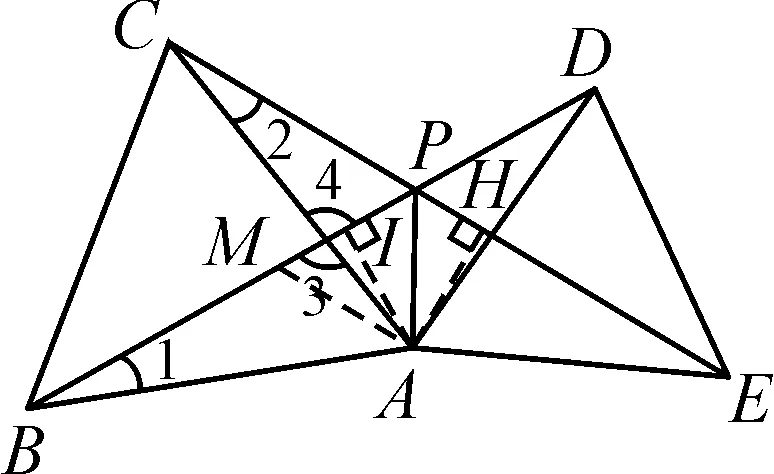
图5

作AI⊥BD,AH⊥CE,I与H分别为垂足.

易证△BAD≌△CAE.

所以∠1=∠2.

又∠3=∠4,所以∠CPB=∠CAB=60°,于是∠BPE=120°.又AI⊥BD,AH⊥CE,则AI=AH(全等三角形对应边上的高相等),所以AP平分∠BPE,则∠BPA=60°.

又PM=PA,则△PMA是等边三角形,所以AM=AP.

所以∠BAC=∠MAP=60°.

易得∠BAM=∠CAP,所以△BAM≌△CAP.

所以BM=PC,故PB=PM+BM=PA+PC.

在截长时,只要截取方式正确,辅助线可以通过多种方式构造,一般都可以得证,比如AM也可以通过作∠PAM=60°的方式出现,先证明△AMP是等边三角形,和证法2相似.

另外,根据题中的条件,易证∠CPB=60°,线段PB也可以按下面的方式截取.

证法3：如图6,在BP上截取PM=PC,连接CM.

图6

易证△BAD≌△CAE,则∠1=∠2.又∠3=∠4,所以∠CPB=∠CAB=60°, 于是△CMP是等边三角形.

所以CP=CM,∠MCP=∠BCA=60°,则∠MCB=∠PCA.又CB=CA,则△BCM≌△ACP,所以BM=PA.

故PB=BM+MP=PA+PC.

3.2 补短法

笔者以延长线段PC的方法作辅助线,证法如下.

证法4：如图7,截取CM=PB,连接AM.

图7

易证△BAD≌△CAE,则∠1=∠2.

又BA=CA,PB=CM,所以△BAP≌△CAM.

所以AP=AM,∠BAP=∠CAM.

易证∠PAM=∠BAC=60°,则△AMP是等边三角形,可知PA=PM.

故PB=CM=PC+PM=PC+PA.

也可通过作角的方式作出这条辅助线,如下.

证法5：如图8,作∠PAM=60°,交CE于点M.作AI⊥BD于点I,AH⊥CE于点H.

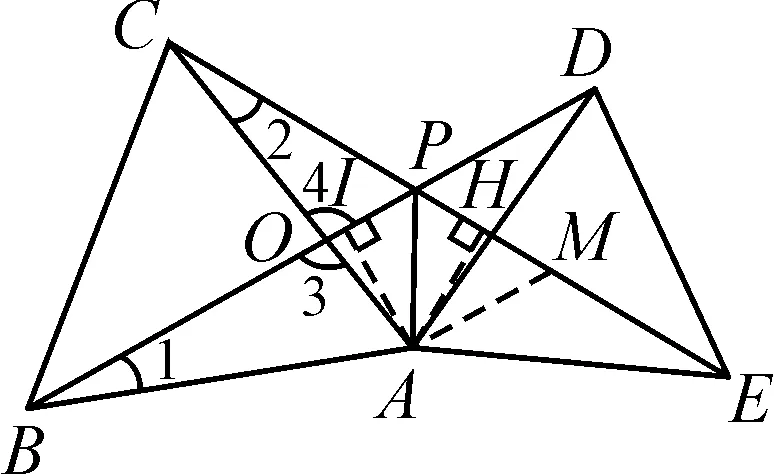
图8

易证△BAD≌△CAE,则∠1=∠2.又∠3=∠4,所以∠CPB=∠CAB=60°,则∠BPE=120°.

又AI⊥BD,AH⊥CE,AI=AH(全等三角形对应边上的高相等),所以AP平分∠BPE,则∠MPA=60°.

所以△PMA是等边三角形,于是有PM=MA,∠PAM=∠CAB=60°.

所以∠CAM=∠BAP,易证△BAP≌△CAM.

故BP=CM=PC+PM=PC+PA.

点M也可以通过截取PM=PA得到,同证法5一样,先证∠MPA=60°,得证△PMA是等边三角形,接着证明△BAP≌△CAM,从而证出结论,证法略.

在延长线段CP时,也可以反向延长,如证法6.

证法6：如图9,延长PC至点M,使PM=PB,连接BM.

图9

易证∠CPB=∠CAB=60°.

所以△PMB是等边三角形,则BM=BP.

所以∠MBP=∠CBA=60°.

易证∠MBC=∠PBA.

又根据CB=AB,易证△CMB≌△APB,所以CM=PA.

故PB=PM=PC+CM=PC+PA.

证法7：如图10,延长PC至点M,使CM=PA,连接BM.

图10

易证∠CPB=∠CAB=60°,所以∠BPE=120°.

又因为AI⊥BD于点I,AH⊥CE于点E,则AI=AH(全等三角形对应边上的高相等),所以AP平分∠BPE,则∠BPA=60°.

所以∠CBA+∠CPA=180°.

所以∠BCP+∠BAP=180°.

又∠BCP+∠MCB=180°,则∠MCB=∠BAP.

又CM=PA,CB=AB,所以△CMB≌△APB,则BM=PB.

又∠CPB=60°,所以△PMB是等边三角形,则PB=PM.

故PB=PM=PC+CM=PC+PA.

对于此题,也可以通过延长PA的方式作辅助线,其他的证明方法这里就不再赘述.

就这道题来说,无论是哪个方法,其证明思路都是通过“截长”或“补短”的方式将问题进行转化,进而得以解决.可见,大多数学生对“截长补短”的证明思路不是很清晰,关键是综合运用几何知识进行推理的能力有所欠缺.这就要求教师应在教学中适当的节点精选教学内容进行专题训练,帮助学生明晰“截长补短“法的思路,引导学生对一题展开多种解法的训练,让学生真正领会“截长补短”法的本质,深刻体会转化的数学思想,发展推理能力和几何直观素养,促进数学学科核心素养的发展.