基于Petri网的全自动无人驾驶列车停站场景形式化建模与验证

王玮琦，任晨宇，陈黎洁，侯卓璞

按照国际通行定义，城市轨道交通自动化等级（Grade of Automation，GoA）划分为5个等级：GoA0～GoA4级。其中，最高等级GoA4级代表了技术发展的趋势，被定义为全自动无人驾驶系统（Unattended Train Operation，UTO）。UTO系统运行时无需司机和乘务员参与，在控制中心的统一调度下实现列车唤醒和休眠、载客运行、洗车及出入停车场等全场景、全过程自动控制，有充分的设备冗余配置和完善的安全防护机制［1］，已成为未来轨道交通发展的必然趋势。

全自动无人驾驶系统中，由自动控制系统替代司机和乘务员操作，降低了由于人为失误导致发生事故的可能性，但是系统组件信息交互频繁、时序特征复杂等特点也带来新的安全风险。一般先由生产厂家对全自动无人驾驶系统进行安全验证，在实验室的仿真环境下测试相关功能，再在新建项目中进行现场系统场景测试。然而，这种方式通常无法检测出各个专业接口之间的潜在问题，在实际运营过程中才能发现一些具体问题［2］。因此，在全生命周期早期对系统中运营场景的实现流程进行建模与验证分析，对于全自动无人驾驶系统的项目实施和安全应用至关重要。

作为一种基于数学和逻辑的系统化方法，形式化方法被广泛应用到轨道交通系统的建模与验证研究中。文献［3］采用STPA（系统理论过程分析方法）对全自动无人驾驶系统中的自动洗车功能进行安全分析，辨识不安全控制行为并提出风险规避措施。文献［4］采用形式化建模工具UPPAAL对LKJ-15系统的模式转换功能进行建模并验证其安全性。文献［5］采用安全状态机对自主化ATP的等级转换功能进行建模，并利用HAZOP（危险和可操作性分析）方法对其进行安全验证。

Petri网是由Carl Adam Petri提出的一种基于状态的形式化建模方法，具有严格的数学定义和直观的图形表达，可以清晰地描述系统状态的动态演变过程，被广泛应用于计算机和系统工程的建模与仿真验证领域。文献［6］基于观察、定位、决策、行动（Observation、Orientation、Decision、Action，OODA）环理论分析无人多平台作战指挥流程，采用Petri网工具对OODA指挥控制进行建模与验证。文献［7］基于城市轨道交通车载ATP子系统建立Petri网故障模型，并进行危险源辨识与故障诊断。文献［8］针对地铁车辆子系统建立Petri网模型，研究其在运营过程中可能发生的安全事故。全自动无人驾驶系统的运营场景是在系统设计阶段分析系统安全关键功能建立的应用实例，Perri网在系统静态结构和动态行为的建模分析方面具有优势，因此本文以一个典型的全自动无人驾驶系统运营场景——列车自动停站场景为研究对象，利用Petri网理论对其进行建模与验证，为系统开发及安全分析提供理论支撑。

1 列车自动停站场景

列车自动停站属于正线运营场景，是全自动无人驾驶系统的关键运营场景之一。全自动无人驾驶系统的运营场景与传统CBTC系统的不同之处在于：传统CBTC系统中，列车停站过程中由驾驶员或站务人员确认车门是否满足关闭条件，列车客室车门的开启/关闭由驾驶员通过按下开门或关门按钮执行；全自动无人驾驶系统没有司机的参与，完全依赖系统实现该功能。

列车进站场景结束之后进入列车停站场景，当列车进站对标停车后，停站倒计时开始。此时站台上的乘客处于站台门之外等候上车，车内乘客在车门处等候下车。车载控制器（Vehicle On-board Controller，VOBC）生成允许开门指令并向车辆发送门控命令，车门控制单元执行开门命令开启车门并将车门开启状态信息反馈给VOBC。与此同时，VOBC向计算机联锁（Computer Interlocking，CI）发送允许开门指令，CI将开门指令发送给站台门系统，站台门门控单元解锁并开启站台门，CI将站台门状态信息反馈给VOBC。当车门和站台门分别开启后，乘客开始上下车。站台门与客室车门的障碍物检测装置开始工作，并将站台门与车门状态实时反馈给VOBC。在时刻表规定的停站时间结束时，且站台门与车门处无异常状态，VOBC即生成关门指令，车门和站台门关闭过程与前文所述开门指令的传输流程一致。当VOBC收到车门和站台门关闭且锁闭、列车与站台门间无异物的状态反馈信息后，允许列车启动出发［9］。至此列车停站场景结束，进入列车离站场景。全自动无人驾驶系统列车停站运营场景事件顺序见图1。

图1 全自动无人驾驶系统列车停站场景事件顺序

由图1可知，全自动无人驾驶系统中的列车停站运营场景由以下子场景按顺序组成：列车进站停车、开启车门与站台门、乘客上下车、关闭车门与站台门、列车启动离站。各子场景中涉及对象主要包括VOBC、CI、列车客室车门、站台门和乘客，各对象的状态随着子场景的改变而发生变化，各子场景中各对象的状态见表1。

表1 列车停站场景各参与对象在不同阶段的状态

2 基于Petri网的运营场景建模与分析

2.1 Petri网基本要素及运行规则

经典Petri网是一个由节点和连接弧所组成的有向二分图。一个Petri网结构由4个基本元素组成：库所（place）、变迁（transition）、有向弧（arc）和令牌（token）。其中，库所和变迁是Petri网的2个节点类型，库所表示被建模的系统状态，变迁表示在系统中发生的事件；有向弧连接库所和变迁，表示两者之间的顺序关系，2个同类型的节点之间不能连接；令牌是分布在库所中的动态对象，可以从一个库所转移到另一个库所，根据触发规则转移，代表系统状态的演化，反映系统运行的全部过程。

在Petri网中，变迁的使能（enabling）表示该变迁代表的事件，在满足前提条件时发生。用变迁的输入库所（由指向变迁的弧所连接的库所）表示该事件发生所需要的前提局部状态，如果一个变迁的每个输入库所都拥有令牌，则该变迁即为被允许（enabled）。一个变迁被允许时，该变迁将被触发（fire）。

2.2 模型建立

对全自动无人驾驶系统运营场景进行Petri网建模的流程如下。

Step 1清晰刻画需要建模的运营场景，即确定场景中事件发生的时序逻辑及状态变化。

Step 2在分析系统运营场景的基础上进行对象状态集辨识，提取出场景中的参与对象，将运营场景分成若干顺序子场景，分析各子场景中参与对象的状态变化及时序逻辑。

Step 3根据所提取对象的状态集和事件确定Petri网中对应库所和变迁的物理含义，严格定义其模型语义，根据事件时序逻辑选择相应的基本结构，建立对应运营场景的Petri网模型。

在对列车自动停站场景建模时，利用库所表示列车停站过程中各参与对象在不同阶段的状态；利用变迁表示列车停站过程中触发不同状态的事件；利用有向弧连接库所和变迁来表示状态时序及事件触发逻辑顺序。根据场景描述分析设计Petri模型的库所集合P为P=｛P0，P1，P2，…，P14｝，变迁集合T为T=｛T0，T1，T2，…，T10｝。列车停站场景Petri网模型中库所集和变迁集标识及对应含义见表2。

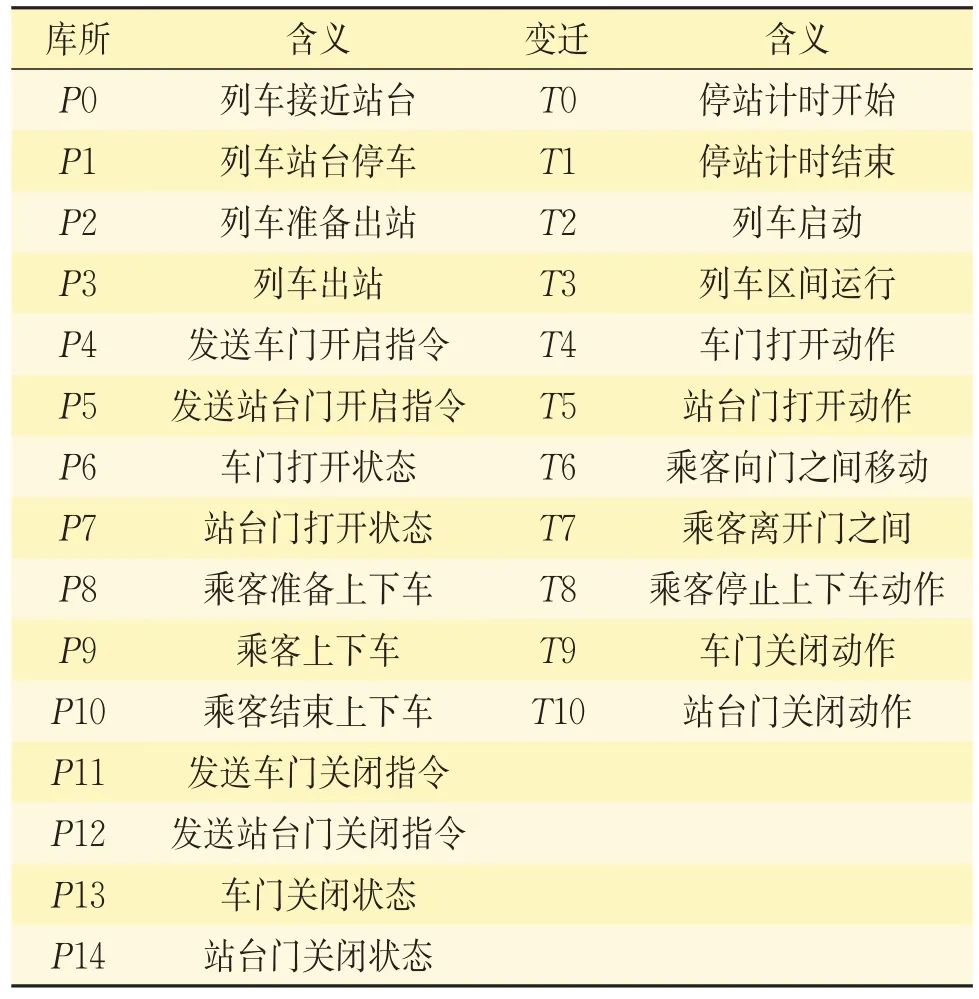
表2 列车停站场景各库所、变迁的编号及对应含义

根据各参与对象状态与库所的对应关系、触发事件与变迁的对应关系，以及列车停站场景流程逻辑时序，基于开源Petri网建模软件PIPE［10］，建立的全自动无人驾驶列车停站场景Petri网模型见图2。

图2 全自动无人驾驶列车停站场景Petri网模型

图2中，元素、符号及物理含义见表3；有向弧上的数字为权重，每条弧的权重相同，为默认值1［11］；库所P0、P1、P2、P3分别为列车从进站、站台停车、准备出站到启动离站这一过程的状态变化；变迁T0、T1分别为列车对标停车后停站计时开始和停站计时结束2个事件；车门控制子场景发生在列车停站过程中，从列车对标停车后开始，到列车停站计时结束后车门与站台门关闭为止，中间伴随着乘客上下车子场景，当车门与站台门均关闭后，列车启动离站，并在区间运行直至接近下一车站，这2个事件分别为变迁T2和T3。

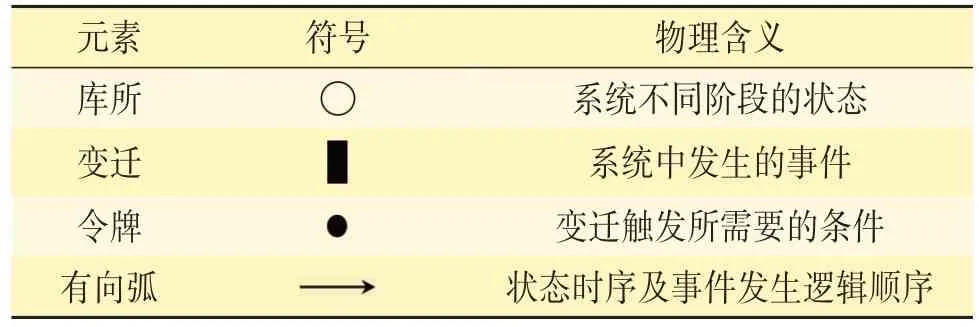
表3 Petri网元素、符号及物理含义

2.3 模型分析

由图2可知，当列车处于停车状态时，进入车门控制子场景，车载设备分别发送客室车门和站台门开门指令，分别由库所P4和P5表示。此处采用Petri网基本结构中的并发结构，即库所P0拥有令牌，通过T0触发后，P4和P5都拥有了令牌，描述车门与站台门开启的并发过程，同时库所P1获得令牌，列车处于停站状态。客室车门和站台门的开门动作分别由变迁T4和T5表示，此时客室车门与站台门处于开启状态，分别由库所P6和P7表示。当车门与站台门都处于开启状态时，乘客开始上下车。变迁T6为车厢里和站台上的乘客开始向车门处移动，此处采用Petri网基本结构中的同步结构，即只有当库所P6和P7都具有令牌时，变迁T6才能被触发。库所P8、P9、P10为站台门和车门开启后乘客上下车子场景中的3个状态，即车门开启后的乘客状态、乘客乘降状态和上下车过程结束后的乘客状态。

为了更清晰地将乘客上下车过程中的库所与变迁关联起来，将乘客上车与下车动作转换为上下车乘客进入门之间与离开门之间的2种动作，分别由变迁T6和T7表示，描述乘客上下车过程的库所与变迁示意见图3。此处采用Petri网基本结构中的顺序结构，即变迁T6触发后，库所P8拥有令牌，按乘客上下车时序逻辑触发变迁T7，使库所P9拥有令牌并保持，直到车门与站台门关闭。列车停站时间结束时，触发变迁T1，此时车载设备发送车门和站台门关闭指令，分别由库所P11和P12表示，此处采取的结构与车门开启过程相同，即变迁T1触发后，库所P11、P12、P2同时拥有令牌。客室车门及站台门关闭动作由变迁T9与T10表示，车门与站台门关闭后的状态由库所P13和P14表示。库所P9、P13、P14同时获得令牌后，变迁T8被触发，即乘客停止上下车动作，库所P10获得令牌，表示上下车场景结束后的乘客状态。当库所P2、P10同时拥有令牌后，变迁T2被触发，即当车门与站台门关闭后，乘客结束上下车，允许列车启动离站。库所P3获得令牌表示列车出站状态，触发变迁T3后，库所P0重新获得令牌，开始新一轮的列车停站场景。

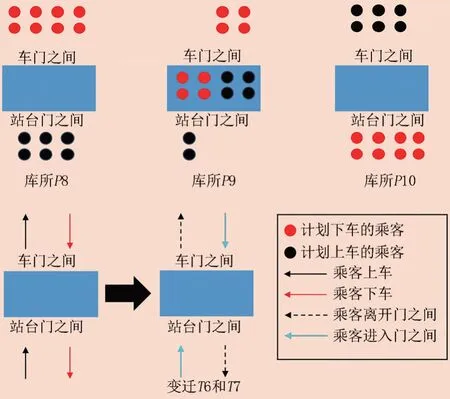
图3 乘客上下车场景库所与变迁示意

综上，列车自动停站场景Petri网模型由顺序、并发和同步3种基本结构组成。其中，顺序结构描述列车停站、列车运行、乘客上下车和车门控制等子场景；同步结构描述变迁的触发条件，例如车门和站台门都开启后乘客才可以上下车，车门与站台门关闭后意味着乘客停止上下车；并发结构描述场景状态的并发特点，例如停站倒计时开始后车载设备同时发送客室车门和站台门开门指令，同时列车处于停站状态；列车启动后，停站场景结束，列车在区间运行并接近站台，进入下一个停站场景。

3 模型验证与优化

本文应用Petri网建模软件PIPE对所建模型进行验证，并考虑场景中可能出现的异常情况，对模型进行优化。

3.1 模型验证

评价Petri网的可用性指标一般包括可达性、有界性、安全性及活性。

定义一个库所集P，p∈P在一个Petri网的每一个库所p中令牌数量不超过一个有限正整数k，库所与其所包含的令牌数的映射函数为M（p）。当M（p）≤k，则判定该库所是有界的，k为该库所的界。当k=1时，则称该库所是安全的。如果Petri网中每个库所都有界，则该Petri网有界，当Petri网的界为1时，则称该Petri网是安全的［12］。

定义一个变迁集T，对于Petri网中的任意变迁t⊂T，若存在某个变迁序列覆盖该变迁，即该变迁是被允许的，则称该变迁是活的。若一个Petri网所有变迁是活的，则该Petri网具有活性，与之相反的现象则称为死锁。

首先，利用PIPE软件中的可达图模块自动生成上述Petri模型状态空间可达图，见图4。图4中，节点S为模型的可达标识集，即系统从初始状态经过一系列变迁的触发和令牌的转移达到最终状态的全部状态集合。可达标识由具有令牌的库所构成，初始标识S0=｛P0｝，终止标识S32=｛P3｝。可达标识之间由带约束的有向弧连接，约束为触发的变迁，例如初始标识S0经过变迁T0到达标识S1。模型覆盖所有变迁，不存在死锁，因此所建模型具有活性。从图4可以看出，系统模型在不同子场景中至少存在1条可达路径，保证能够成功执行模型中的各项功能，模型从起始节点到终止节点存在可达路径，因此所建Petri网模型具有可达性。

图4 Petri网模型状态空间可达图

其次，利用PIPE软件不变量分析模块（Invariant Analysis）得出所建模型的变迁不变量（T-invariants）、库所不变量（P-invariants）及不变量方程。模型不变量分析结果见图5。由图5可见，所建Petri网中有1个变迁不变量和5个库所不变量。对于变迁不变量，分析模块给出的结论是：该网络被确定的T-invariants覆盖，因此它可能是有界和活的。对于库所不变量，分析模块给出的结论是：该网络被确定的P-invariants覆盖，因此它是有界的。

图5 模型不变量分析结果

根据Petri网中的5个库所不变量，仿真模块给出对应的5个库所不变量方程。图5中｛M（Px），x=0，1，2，…，14｝为库所与其所包含的令牌数的映射函数。由库所不变量方程可知，Petri网的界为1，根据Petri网的有界性和安全性定义可知，所建Petri网是有界和安全的。图6所示的由PIPE软件状态分析模块（State Space Analysis）得出的结论为模型有界、安全、无死锁，同时也验证了上述分析结果。

图6 模型状态空间分析结果

综上，由仿真验证和状态空间分析结果可知，根据场景需求和对象状态辨识所建立的全自动无人驾驶系统列车停站运营场景Petri网模型具有可达性、活性、安全性和有界性，验证了所建模型的有效性和可用性。

3.2 模型优化

上述模型只考虑了各设备正常运行时的状态转换，未考虑异常情况的处理与建模分析。在城轨车门控制系统中，原则上要求车门和站台门同时开启或关闭。当处于交通高峰期时，车站内乘客较多，开门时，若车门早于站台门开启，或关门时，站台门早于车门关闭，乘客在上下车过程中，就可能因为拥挤而处于站台门与车门的缝隙中，存在安全隐患。本文针对这类异常情况对上述列车停站模型进行优化。

由于站台门和车门的开门响应时间不同，在实际运行中，目前通过设定车门与站台门延时时间差来确保车门不应比站台门先开启，站台门不应比车门先关闭［13］。根据该思想，优化后的模型见图7。本模型中不考虑设定站台门与车门延时时间差，仅考虑开关时序逻辑。为了避免出现车门比站台门先开启或站台门比车门先关闭的异常情况，本模型中引入库所P15和P16，利用Petri网的并发与同步结构优化车门与站台门的开关时序。在变迁T4和T5之间加入库所P15，表示站台门打开且车门关闭的瞬时状态，P4和P5同时拥有令牌后，T5先被触发，P15和P7获得令牌，只有当P15和P4同时拥有令牌时，T4才被触发，实现变迁T5的触发优先权。同理在变迁T9和T10之间加入库所P16，表示车门关闭且站台门打开的瞬时状态，实现变迁T9的触发优先权。利用PIPE软件中的状态空间分析模块对优化后的模型分析可得，该模型有界、安全、无死锁。

图7 优化后的列车停站场景Petri网模型

4 结束语

通过分析全自动无人驾驶系统列车停站运营场景，基于Petri网理论定义了场景状态的时序和事件触发的逻辑顺序与库所集、变迁集的对应关系，建立了列车停站场景的Petri网模型；利用仿真软件分析与验证了所建模型的有效性及可用性，并针对可能出现的车门/站台门开关时序异常情况对模型进行优化。后续研究可利用有色Petri网、时间Petri网等高级Petri网理论对该模型进行扩展，并对其他运营场景建模并验证，为全自动无人驾驶系统的安全分析和应用提供理论支撑。