可靠响应表示增强的知识追踪方法*

赵 琰,马慧芳,王文涛,童海斌,贺相春

(1.西北师范大学计算机科学与工程学院,甘肃 兰州 730070;2.西北师范大学教育技术学院,甘肃 兰州 730070)

1 引言

近年来,随着大规模在线开放课程MOOC(Massive Open Online Course)[1]和在线评测OJ(Online Judge)系统[2]等教学辅助平台的涌现,用户产生和积累的学习数据由平台所收集。通过分析和挖掘这些教育数据来制定更好的教育教学方案是一项十分重要且富有挑战性的任务,因此受到了研究人员的广泛关注[3]。其中,知识追踪作为教育数据挖掘领域中的任务之一,旨在利用可观测到的学生历史交互数据来评估学生的动态知识状态,从而为学生提供更好的、个性化的学习资源[4]。

随着深度学习在自然语言处理、图像识别等领域取得了不错的效果,许多研究人员将深度学习也应用到知识追踪方法中,主要可以归纳为以下2类:一类是不使用专家标注的习题与知识点之间的关联信息而是直接对学生知识状态进行估计的方法。例如Piech等人[5]率先提出了深度知识追踪DKT(Deep Knowledge Tracing)方法,将循环神经网络应用于知识追踪任务中,并特别提出利用长短期记忆网络LSTM(Long Short-Term Memory)[6]来追踪学生知识水平随时间的变化过程。此外,Zhang等人[7]采用记忆增强神经网络MANN(Memory Augmented Neural Network)提出动态键值记忆网络DKVMN(Dynamic Key-Value Memory Networks)方法。该方法用键矩阵和值矩阵分别存储知识点信息和学生的知识状态信息,通过特定的读取与写入机制,可以直接评估学生随时间变化的知识状态信息。Ghosh等人[8]提出上下文感知的注意力机制知识追踪AKT(Attentive Knowledge Tracing)方法,引入指数衰减项来计算注意力系数,降低时间跨度较大的习题对最终预测的重要性。尽管上述方法在性能上优于传统知识追踪方法,但都未对学生-习题空间、习题-知识点空间进行深入分析,因此这些方法评估出的学生知识状态不具有可解释性。而随着与知识追踪相关研究的开展,另一类方法充分挖掘了学生-习题空间、习题-知识点空间之间的复杂交互关系。Huo等人[9]提出了一种带有上下文信息的习题编码方法LSTMCQ(LSTM based Contextualized Q- matrix),其加入习题和知识点之间的关联信息得到嵌入上下文信息的CQ矩阵,进而对知识点进行上下文化。然而,这些方法都未对习题进行细粒度的表示,使最终得到的学生知识状态不够准确。

针对以上问题,本文设计了可靠响应表示增强的知识追踪KTR(Knowledge Tracing via reliable response Representation)方法。该方法不仅捕获了由学生-习题-知识点关系得到的学生-知识点空间的可靠性,且解决了其存在的高维稀疏性问题,同时还区分了学生在习题上的作答情况,进而得到可靠响应表示。具体来说,首先基于学生的不同作答情况细粒度地划分学生-习题空间,并利用其与习题-知识点空间的交互关系得到与作答情况对应的2种学生-知识点空间;接着,从学生-知识点空间的相对可靠性和绝对可靠性2方面得到学生-知识点空间的可靠性,并利用维数约减方法获得2种可靠且低维的学生-知识点空间;其次,结合学生在习题上的作答情况和构建的可靠且低维的学生-知识点空间得到习题的可靠响应表示;最后,基于长短期记忆网络LSTM和得到的可靠响应表示对学生在不同时刻的知识状态进行追踪。在4个真实数据集上的实验结果表明,本文能够有效地得到习题的可靠响应表示,并且能较好地估计学生知识状态。

2 基础知识

2.1 问题定义与符号说明

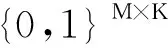
此外,为了描述清晰起见,本文涉及到的常用符号定义总结如表1所示。

Table 1 Commonly used notations definition表1 常用符号定义

2.2 习题-知识点空间和学生-习题空间

习题的相关性建模和学生的作答情况建模是对学生实现个性化认知诊断评估的重要因素。具体地,对于建模习题之间的相关性,Tatsuoka等人[10]最早在数学概念上研究习题-知识点空间Q的影响,利用Q来建模习题和知识点之间的联系。在实际应用中,通常由专家对Q进行标注,表明每一道习题所考察到的知识点,如表2所示。

Table 2 Q matrix about the correlations between exercises and concepts表2 习题和知识点之间的关联Q矩阵

此外对于建模学生的作答情况,常用的方法是利用学生-习题空间R去表征每一个学生与所有习题的交互情况,具体如表3所示。

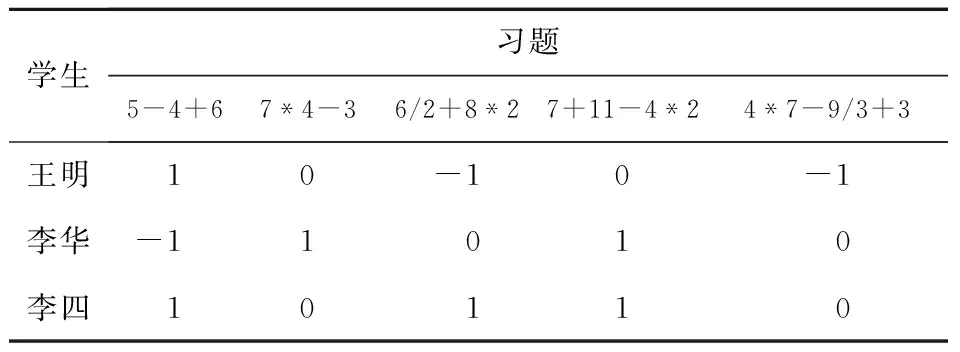
Table 3 Students’ response matrix R表3 学生的响应矩阵R

2.3 维数约减

维数约减通过挖掘数据本质规律、发现内在关系,来简化数据,减少计算成本,并且提高计算效率,其广泛应用于信号处理、模式识别和数字图像处理等领域。

奇异值分解SVD(Singular Value Decomposition)是线性代数中的一种用于降低数据维度的矩阵分解技术。该技术通过发现重要维度的特征,从而减少在数据处理过程中不必要的属性,在实际应用场景中,通常抽取前10%的奇异值便能包含超过90%的信息大小[11]。

2.4 方法框架

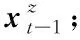
Figure 1 Framework of reliable response representation-enhanced knowledge tracing图1 可靠响应表示增强的知识追踪方法框架

3 KTR方法细节

3.1 可靠且低维的学生-知识点空间

本节基于学生-习题空间和习题-知识点空间得到的学生-知识点空间,并考虑学生-知识点空间的相对可靠性和绝对可靠性,以及利用SVD维数约减方法构建可靠且低维的学生-知识点空间。

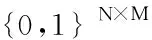
Az=RzQ

(1)

其中,z∈{true,false}且Az∈RN×K。

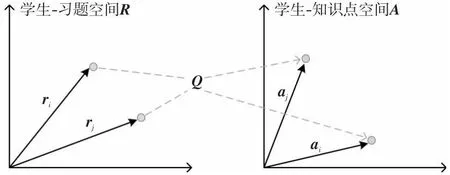
Figure 2 Illustration of the relationship between three spaces图2 3种空间之间的关系

然而,N个学生在特定知识点ck涉及的习题上作答数量不同,并且对于K个知识点,特定学生si在这些知识点涉及的习题上作答数量也不同。直觉上,N个学生在知识点ck涉及的习题上的N个作答数量中,值越大的相对越可靠。同样地,学生si在K个知识点涉及的习题上的K个作答数量中,值越大的也相对越可靠。因此,分别从学生和知识点角度获得学生-知识点空间中元素的相对可靠性是很有必要的。

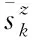
(2)

(3)

其中,I(·)表示指示函数。

然后,利用式(4)和式(5)分别获得学生和知识点角度下,学生-知识点空间中元素对应的相对可靠性:

(4)

(5)

其中,选择y= 1- exp(-x)的目的在于该函数能够合理地捕获数值在区间[1,10]中元素的可靠性(即该区间中元素的值越大对应的可靠性越高),而学生-知识点空间中不大于上述2种平均值的元素基本处于该区间内。因此,式(4)和式(5)能够合理地得到学生和知识点角度下,学生-知识点空间的相对可靠性,分别记为ASRRz和ACRRz。

此外,N个学生在K个知识点涉及的习题上有N×K个不同的作答数量,直觉上,作答数量越大,该值越可靠。因此,可由式(6)直接得到学生-知识点空间中每个元素的绝对可靠性:

(6)

其中,σ(·)表示Sigmoid函数。同样地,可以获得学生-知识点空间的绝对可靠性,记为AARz。

接着,基于学生-知识点空间的相对可靠性和绝对可靠性,得到可靠的学生-知识点空间,如式(7)所示:

ARELz=ANORz⊙ASRRz⊙ACRRz⊙AARz

(7)

其中,ANORz表示对Az进行行归一化和列归一化,⊙表示不同空间中相同位置的元素相乘。

最后,考虑到学生-知识点空间的稀疏性和高维性,故利用SVD维数约减方法降维。因此,通过式(8)分解ARELz:

ARELz=N·Σ·KT

(8)

其中,N∈RN×N、Σ∈RN×K和K∈RK×K分别表示分解后的学生空间、对角值空间以及知识点空间。本文选择Σ前N′个对角值所对应在N中的行构成N′∈RN′×N。至此,可靠且低维的学生-知识点空间可计算如下:

ASVDz=N′·ARELz

(9)

其中,ASVDz∈RN′×K中每一列表示对应知识点的低维表示。

接下来,将给出一种结合学生作答和可靠且低维的学生-知识点空间,以得到习题的可靠响应表示方法。

3.2 基于作答的可靠响应表示

已有的方法中,习题对应的嵌入维度往往为习题数量的2倍,且用独热(one-hot)向量进行表示。这导致习题向量高维且稀疏,从而使得方法预测学生水平的性能降低。为此,本节借助可靠且低维的学生-知识点空间以及学生作答来获得每道习题在2种作答下的响应表示。

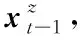
(10)

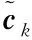
3.3 基于可靠响应表示的知识追踪

对于3.2节得到的可靠响应表示,本节将其作为LSTM的输入,从而评估学生的知识状态。如式(11)～式(16)所示:

(11)

(12)

(13)

(14)

ht=ot∘tanh(ct)

(15)

(16)

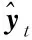
因此,学生si在t时刻正确回答习题的概率如式(17)所示:

(17)

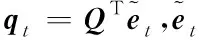
随后,可使用交叉熵损失函数来拟合学生作答记录和KTR方法预测结果之间的偏差。对于学生i的损失函数可建模为式(18)所示:

(18)

其中,rt表示学生在t时刻的真实作答记录。在建立损失函数之后,本节利用随机梯度下降SGD(Stochastic Gradient Descent)算法[12]来最小化损失函数。

综合上述过程,得到KTR方法的伪代码如算法1所示。

算法1 KTR方法输入:学生集合S、习题集合E和知识点集合C,习题-知识点空间Q,学生-习题空间R。输出:学生在t时刻正确回答下一道习题et的概率^rt。1:基于学生作答记录的对错情况将学生-知识点空间R划分为Rtrue和Rfalse;2:根据习题-知识点空间Q,利用式(1)得到作答为对或错的记录对应的学生-知识点空间Az;3:for i = 1 to N4: for k = 1 to K5: 利用式(2)和式(4)计算在学生角度下,学生-知识点空间的相对可靠性ASRRzik;6: 利用式(3)和式(5)计算在知识点角度下,学生-知识点空间的相对可靠性ACRRzik;7: 利用式(6)计算学生-知识点空间的绝对可靠性AARzik;8: end for9:end for10:根据式(7)获得可靠的学生-知识点空间ARELz;11:根据式(8)和式(9)得到可靠且低维的学生-知识点空间ASVDz;12:根据式(10)得到习题对应的可靠响应表示xzt-1;13:根据式(11)～式(17)得到学生在t时刻正确回答下一道习题et的概率^rt;14:利用SGD更新KTR方法参数,直到式(18)中损失函数收敛。

4 实验与结果分析

为了验证本文方法的有效性与合理性,本节设计实验进行验证,实验将回答以下几个问题:

问题1:KTR方法与现有的一些知识追踪方法相比,性能方面存在哪些优势?

问题2:KTR方法中学生-知识点空间的可靠性和维度约减分别对该方法最终性能有何影响?

问题3:KTR方法中习题的可靠响应表示有怎样的特点?

问题4:在真实数据集上,KTR方法评估的学生知识状态是否具有可解释性?

在本节中,首先给出实验所使用的数据集;其次介绍实验设置与基线方法;然后根据所提问题对评价指标进行介绍;最后对实验结果进行分析并结合案例分析阐述本文方法的有效性和合理性。

4.1 实验数据集描述

实验所用的4个公开数据集为:Assist2009(https://sites.google.com/site/assistmentsdata/)、Assist2017(https://pslcdatashop.web.cmu.edu/KDDCup/downloads.jsp)、KDD Cup Algebra2005以及Statics2011(https://pslcdatashop.web.cmu.edu/DatasetInfo?datasetId=507)。各个数据集的详细信息如下所示:

(1)Assist2009数据集是2009年和2010年由ASSISTment在线教育平台所收集的,是知识追踪相关论文中使用最广泛的数据集之一[13]。由于原始数据集中有大量重复的交互记录存在,于是预处理时删除了重复部分,得到的最终数据集包含4 163名学生的324 572条作答记录,其中与学生交互的习题分别来自于123个不同的知识点。

(2) Assist2017数据集与Assist2009类似,也是来源于ASSISTment在线教育平台。不同的是,该数据是由平台在2017年收集的,包含1 709个学生的392 000条作答记录,其中知识点个数为102个。

(3)Algebra2005数据集来自于KDD Cup 2010年教育数据挖掘挑战赛,这是一个在2005年和2006年收集的代数练习序列数据集[14]。该数据集有809 694条作答记录、437个知识点、574名学生和1 085道习题。

(4)Statics2011数据集是从大学的工程力学课程中收集的[15]。删除学生在同一习题上的多次作答后,数据集包含987道习题、61个知识点以及来自316名学生的135 338条作答记录。

表4给出了上述4个数据集的详细统计信息。

Table 4 Statistics of four real-world datasets表4 真实数据集统计信息

4.2 实验设置与基线方法

4.2.1 实验设置

实验将4个数据集划分为训练集和测试集,其中训练集为80%,测试集为20%。为了确保实验结果的可靠性,实验对所有方法和所有数据集采用5次5折交叉验证法来评估KTR方法的性能。

在KTR方法的训练阶段,设置最大序列长度max_step为50,学习率learning_rate为0.002,训练轮数epoch为260,每批数据大小batch_size为64。实验使用Xavier参数初始化方法[16]初始化参数,其对权重初始化的随机值采样于均值正态分布N(0,std2),其中,0表示均值,std2表示方差。此外使用SGD优化器来训练该方法。实验代码由Python实现,并且实验在操作系统为Linux,显卡为NVIDIA®Quadro RTXTM6000服务器上运行。

4.2.2 基线方法

本文选择以下2类方法作为对比方法。第1类方法仅利用学生的作答记录而未考虑习题-知识点空间,包括DKT、DKVMN和AKT-R(AKT method with the Rach model-based embedding);第2类方法在使用学生作答记录的同时还加入习题-知识点空间的信息,包括LSTMCQ。具体情形如下所示:

(1)DKT[5]:这是一个开创性的方法,使用单层LSTM对学生知识状态的学习进行建模,进而预测学生的表现。其中习题用2M维的one-hot向量进行表示。

(2)DKVMN[7]:一种基于记忆增强循环神经网络的方法,其中不同知识点之间的关系由键矩阵表示,学生对每个知识点的掌握程度由值矩阵表示。

(3)AKT-R[8]:受到认知和心理测量模型的启发,该方法使用了一种新的单调注意力机制,将学习者对评估习题的未来反应与他们过去的反应联系起来。此外,该方法使用Rasch模型来规范知识点和习题的表示。

(4)LSTMCQ[9]:这是在DKT的基础上提出的一种习题编码方法,利用上下文表示方法对领域专家创建的习题-知识点空间Q进行重表示。

4.3 评价指标

由于无法得到学生真实的知识状态,因此对于知识追踪方法来说很难对其性能进行评估。遵从现有的工作,实验通过预测学生的做题情况来得到追踪结果,进而与学生的真实作答情况对比,最终间接地实现对知识追踪方法的评估。因此,实验将用回归(即均方根误差RMSE(Root Mean Squared Error))、分类(评价指标包括ACC(ACCuracy)和AUC(Area Under the ROC Curve))指标来评估KTR方法和基线方法的性能。评价指标定义如下:

均方根误差RMSE通过预测值和学生真实作答情况得到,计算方法如式(19)所示:

(19)

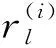
准确率ACC通过如表5所示的混淆矩阵计算得到,定义为分类正确的样本数量占样本总数的比例,如式(20)所示:

(20)

表5中方法预测值超过0.5时视为正例,否则为负例。ACC值越高,方法性能越好。

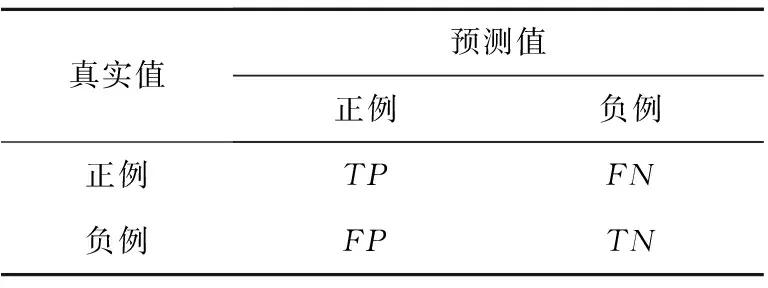
Table 5 Confusion matrix表5 混淆矩阵

此外,引入ROC曲线下面积AUC,其取值为0～1,值越大,方法的表现越好。

4.4 结果分析

4.4.1 性能比较(问题1)

为了验证本文方法的性能,本节利用5次5折交叉验证法对各方法在4个数据集上得到的各评价指标数据取平均值后,得到如表6所示的最终结果。

表6显示了不同数据集上本文方法与各对比方法在ACC、AUC以及RMSE上的表现。从表6中可以看出,首先利用学生作答记录和习题-知识点空间信息的方法性能基本优于未使用习题-知识点空间的信息的方法。这是由于习题和知识点之间的信息弥补了仅利用作答记录方法的不足,从而对方法的性能有了一定的提升。其次,KTR方法要优于LSTMCQ方法,这说明相较于对知识点进行上下文表示,本文基于低维且可靠的学生-知识点空间和学生作答记录得到的可靠响应表示更有效,使KTR方法性能有所提高。

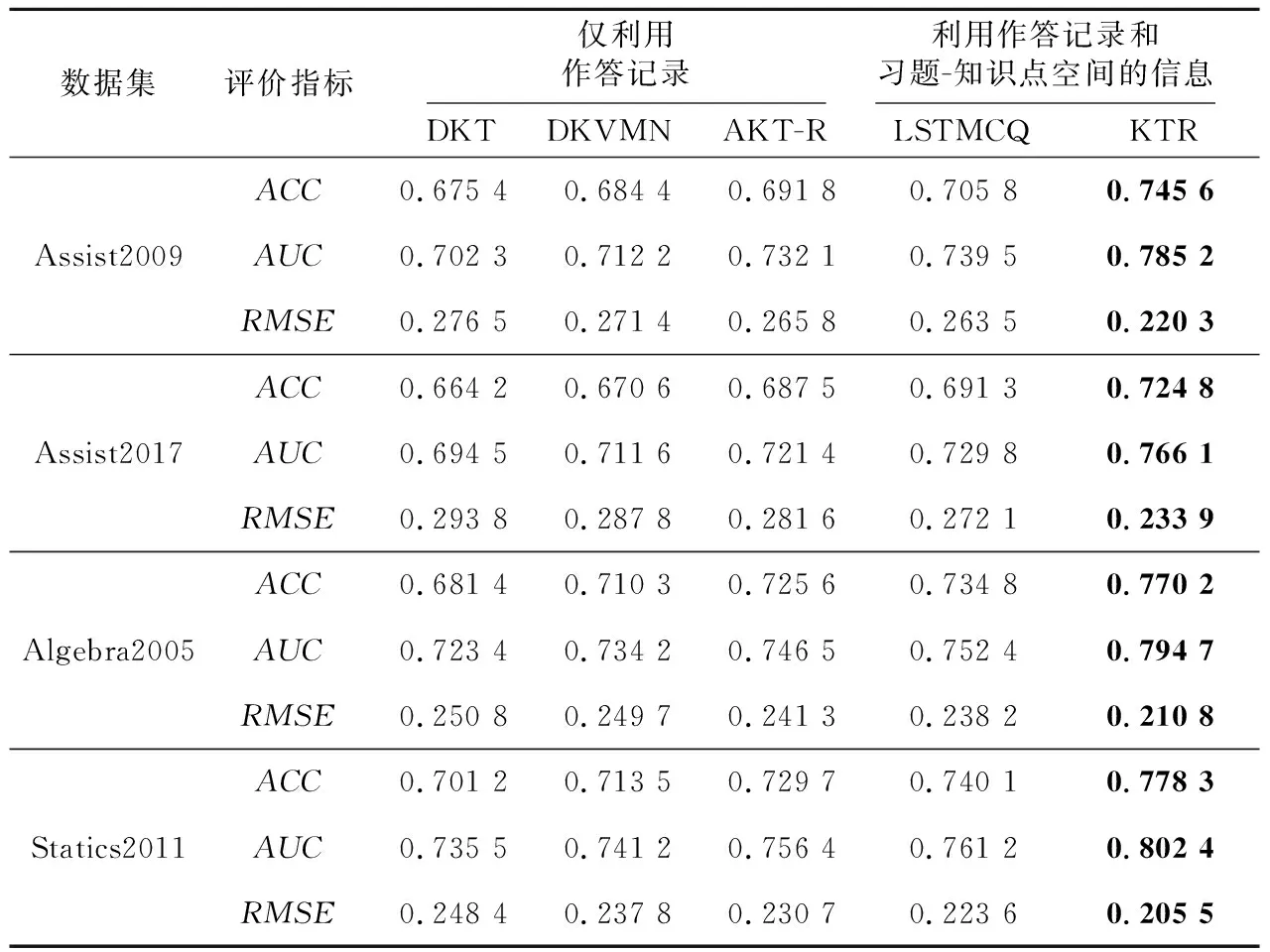
Table 6 Comparison of this method with other baseline methods表6 本文方法与其他基线方法的对比

4.4.2 消融研究(问题2)

为了评价KTR方法中学生-知识点空间的可靠性和维度约减对该方法最终性能的影响,此处用KTR-REL表示未考虑学生-知识点空间的可靠性,仅考虑其维度约减,故只得到低维的学生-知识点空间。另外,用KTR-DR表示未考虑学生-知识点空间的维度约减,仅考虑其可靠性,故只得到可靠的学生-知识点空间。

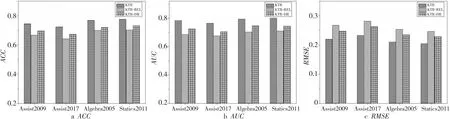
Figure 3 Performance comparison of ablation study on four datasets图3 4种数据集上消融研究的性能表现

从图3中可以看到,KTR-REL或KTR-DR方法的ACC、AUC及RMSE相比于KTR方法的都有了一定程度的性能下降,这表明学生-知识点空间的可靠性和维度约减对KTR方法的性能预测是缺一不可的。其次,KTR-REL方法相比KTR-DR方法在3个性能指标上下降更快,说明学生-知识点空间的可靠性对KTR方法性能预测的贡献更大。总之,同时考虑学生-知识点空间的可靠性和维度约减可实现KTR方法的最佳性能。

4.4.3 习题的可靠响应表示研究(问题3)

为了探究KTR方法中习题的可靠响应表示的特点,本节分别从Assist2009数据集的作答记录为对和错的习题集中随机选取200道习题,并利用t-SNE技术将这400道习题对应的可靠响应表示投影到二维平面。如图4a和图4b所示,这2种可靠响应表示有相似的聚类特点,即相同知识点的习题对应的响应表示聚类在一起。上述观察也是符合具有相同或相似知识点的响应表示应该更接近的认知,这表明本文方法可得到合理的可靠响应表示。

Figure 4 Visualization of reliable response representation of exercise under two responses图4 2种作答下习题的可靠响应表示的可视化

4.4.4 案例研究(问题4)

本节通过设计一个案例来分析KTR方法评估的学生知识状态的可解释性。图5给出了KTR方法在Assist2009数据集的学生作答记录中捕获编号为366的学生知识状态的案例。从图5中可以观察到,学生连续作答了涉及3个不同知识点(“整数加法”“绝对值”和“解不等式”)的10道习题,并给出由KTR方法获得的该学生在不同时刻正确回答习题的预测概率。

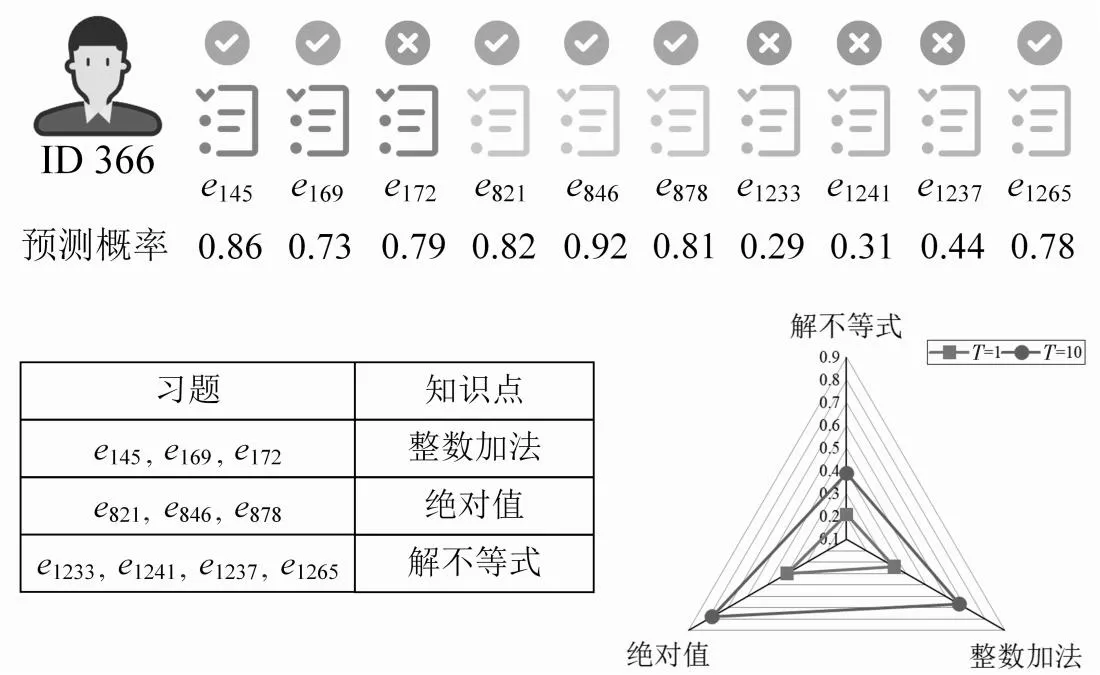
Figure 5 Process of knowledge state of student with ID 366 captured by KTR图5 KTR方法捕获编号为366的学生知识状态的过程

从图5中可以发现,KTR在连续正确预测该学生错误回答习题e1233,e1241,e1237后,还能准确地预测该学生在习题e1265上作答正确。其次,学生在习题e172上的预测概率(即0.79)和真实作答(即错误)不一致,这可能由学生作答时失误导致的。最后,从图5右下方的雷达图可以发现,从T=1时刻到T=10时刻,学生在各个知识点的熟练度有一定的提升。其中,学生在知识点“整数加法”和“绝对值”上的熟练度提升明显,这是由于学生能够连续正确地作答这2个知识点所涉及的习题。但是,学生在知识点“解不等式”上的熟练度提升不明显,这是因为学生在T=7到T=9时刻都错误地作答了习题e1233,e1241,e1237,仅在T=10时才正确作答e1265。因此,本文方法评估的学生知识状态具有较好的解释性。

5 结束语

本文针对现有方法存在未考虑基于学生-习题-知识点关系构建的学生-知识点空间的不可靠性和高维稀疏性,以及未结合学生在习题上的作答结果生成习题对应的可靠响应表示的问题,提出可靠响应表示增强的知识追踪方法。该方法不仅捕获了学生-知识点空间的可靠性,并解决了其具有的高维稀疏性问题,同时还基于学生在习题上的2种作答情况得到习题的可靠响应表示,进而更好地评估学生在各个知识点上的知识水平。在4个真实数据集上的大量实验结果表明,本文方法对于估计学生知识水平具有有效性以及可解释性。在未来的工作中,将继续探究复杂多样的学习数据,例如,习题考察的每个知识点的作答情况、学生的猜测失误行为,以及习题个性化的难度信息等,以便更精准地预测学生表现。