移动边缘计算中计算卸载与资源分配联合优化策略*
刘向举,李金贺,方贤进,王 宇
(安徽理工大学计算机科学与工程学院,安徽 淮南 232001)
1 引言
随着物联网和无线通信技术的快速发展,各类移动设备得到大量普及,越来越多先进的无线应用被广泛应用于智能设备中,如无人驾驶、电子医疗、在线游戏等[1,2]。然而,移动设备由于物理尺寸通常较小,电池容量和计算能力有限[3],当移动设备同时处理多个应用任务时,可能无法满足用户对低时延和低能耗的需求。如何满足用户任务日益增长的计算资源需求,成为一个迫在眉睫的问题。移动边缘计算MEC(Mobile Edge Computing)[4]作为一种新的分布式计算范式应运而生。通过在移动网络边缘部署高性能的MEC服务器,可以让云计算功能更有效、无缝地实现到移动网络中,为用户设备、移动运营商和服务提供商等提供便利[5]。
MEC中的卸载决策和资源分配在减少执行任务的能耗和时延方面,发挥着重要作用。目前在卸载决策研究方面,按照任务卸载的方向,可以分为设备到边缘和边缘到云。
(1)设备到边缘。对于需要强大容量或边缘数据聚合的应用,移动设备将他们的任务卸载到MEC服务器,可以为移动设备实现不同的需求。为了减少任务处理延迟,文献[6]考虑了子任务之间的依赖关系以及边缘用户之间的竞争,提出了一种轻量级的卸载方案,有效地减少了物联网应用程序的整体应用延迟。为了降低移动设备在最坏情况下的能耗,文献[7]利用极值理论来界定不确定事件的发生概率,研究了受应用程序执行时间影响的计算卸载问题。文献[8]通过博弈论提出了一个计算卸载决策方案,用于计算均衡的多项式复杂度算法,目的是最小化延迟和能耗的组合成本,以确定是否将终端设备的任务卸载到MEC服务器。文献[9]针对车联网中单个MEC服务器无法有效解决车辆资源不足的问题,提出了一种多MEC服务器的联合卸载方案,有效降低了整体任务失败率。
(2)从边缘到云。从移动设备卸载的任务一般由边缘层的计算节点处理,如果边缘层的任务数据不能被计算节点及时处理,可以进一步卸载到云中心,以实现平衡过载。这种从边缘到云的卸载方向,实际上是在边缘-云协作方式下操作的。文献[10]针对云-边缘计算网络,提出了一种基于博弈论的计算卸载方法,采用逆向归纳法对提出的博弈进行了分析,设计了一个基于梯度的迭代搜索算法来获得最优解。文献[11]为了利用MEC系统中的有限资源,提出了一种云-边-端协同任务卸载框架,结合人工蜂群ABC(Artificial Bee Colony)算法和粒子群优化PSO(Particle Swarm Optimization)算法设计了人工粒子蜂群APS(Artificial Particle Swarm)算法,以求解卸载决策,该方案有效降低了时延和能耗。但是,上述文献都没有考虑对卸载决策后的资源进行分配。
有效的资源分配可以进一步提高卸载的效果,相关研究人员考虑联合优化卸载决策和资源分配。文献[12]为了实现延迟最小化的工作负载优化分配,提出了平衡初始化、资源分配和任务分配算法,有效地降低了服务延迟。文献[13]研究了多用户协同移动边缘计算网络中的卸载决策、协作决策、计算和通信资源分配的问题,提出一种两级交替方法,解决了公式化的MINLP(Mixed Integer Non-Linear Program)问题,仿真结果表明,该方法在能量效率和任务完成率上均取得了优异的性能。文献[14]针对医疗物联网场景,提出了一种基于组合拍卖和改进粒子群优化的电子医疗计算卸载方法,以满足医疗监测中低时延、低能耗的服务质量QoS(Quality of Service)要求。文献[15]为了最小化物联网节点的总能耗,研究了多用户卸载、传输功率和MEC资源的联合分配问题,然后基于问题的解耦和KKT(Karush-Kuhn-Tucker)条件导出的表达式解决了该问题。
上述研究在不同的约束条件和场景中都能取得很好的效果,在满足用户不同需求、提升用户体验方面取得了进展。但是,上述研究主要针对的是单MEC服务器场景下的计算卸载或资源分配问题。对于多MEC服务器的场景,特别是在制定联合优化的卸载决策、资源分配策略方面,以及如何在能耗和时延之间实现平衡优化方面,上述研究尚未给出具体解决方案。因此,针对当前实际应用场景多由海量智能终端设备、多基站组成的通信环境,本文研究了多用户、多MEC服务器场景下的计算卸载和资源分配问题,并为该场景提出了更广泛的计算卸载解决方案。本文具体工作如下:
(1)考虑了多用户、多基站和多MEC服务器的移动边缘计算网络模型,对通信资源和计算资源进行建模,量化了用户执行任务的时延和能耗,并将用户的时延和能耗的加权和作为优化目标。
(2)提出了联合优化计算卸载和资源分配的问题,考虑到问题的复杂性,将问题解耦为卸载决策和计算资源分配2个子问题。对于计算资源分配问题,采用拉格朗日乘子法;对于卸载决策问题,设计了改进的鲸鱼优化算法,能在短时间内得到问题稳定收敛的最优解。
(3)通过与其他基准方案进行对比,以及在相关参数的变化下对本文所提算法的性能评估,验证了本文所提算法的性能增益。
2 系统模型
考虑一个多用户、多基站和多MEC服务器组成的移动边缘计算场景。如图1所示的MEC系统模型中,每个基站都配备一个MEC服务器,MEC服务器可以是具有计算能力的物理服务器或虚拟机,并通过回程链路与其相关联的基站互连。其中,有S个MEC服务器部署在网络边缘中,将MEC服务器的集合定义为M={mi,i=1,2,…,S}。K个用户的移动设备可以通过无线网络连接基站,将其任务卸载至MEC服务器上,则用户集合定义为N={nj,j=1,2,…,K}。在计算任务卸载的过程中,考虑的是一个移动终端设备不切换接入点的准静态系统[16],即移动设备每次卸载的时间段内,用户设备的组成是不变的。在这个场景中,每个用户有一个移动设备,每个移动设备每次仅有一个任务需要进行处理。
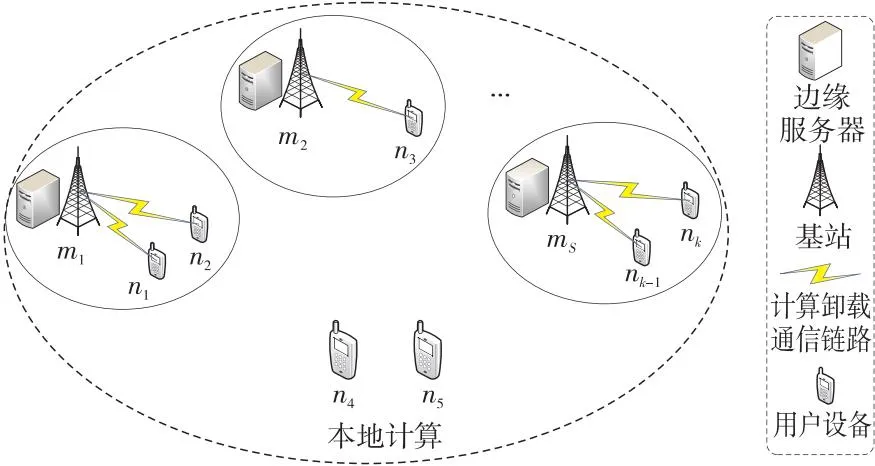
Figure 1 System model of MEC图1 MEC系统模型
由于每个任务可以在用户设备上进行本地处理,也可以卸载到任意一个MEC服务器上进行处理,并且 MEC服务器独立工作,用户的计算任务是不可分割的,定义yj,i∈{0,1}为用户nj的卸载决策。yj,i=1表示用户nj将任务卸载至MEC服务器mi上;否则yj,i=0。本地计算用第S+1个MEC服务器mS+1表示,即yj,S+1=1。因此,K个用户S个MEC服务器的最终卸载结果可以用一个K×(S+1)的矩阵Y来表示,如式(1)所示:
(1)
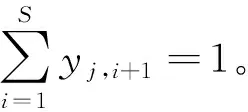
2.1 通信模型
当用户选择卸载处理任务时,基站通过无线信道与移动设备相互连接,实现用户计算任务的上传和下载。采用正交频分多址OFDMA (Orthogonal Frequency Division Multiple Access)技术进行任务传输,用户之间的干扰忽略不计。用户nj到MEC服务器mi的上行数据传输速率如式(2)所示:
i=1,2,…,S,j=1,2,…,K
(2)
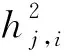
2.2 计算模型
每个用户nj的计算任务的属性用一个二元组表示为Taskj={Dj,Cj}。其中,Dj为用户nj的任务执行数据量;Cj为用户nj的任务计算量,即计算该任务所需的CPU周期数,任务越复杂所需的周期数越多。
2.2.1 本地计算模型
(3)
(4)
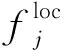
2.2.2 卸载边缘计算模型
当用户的计算任务选择由MEC服务器进行处理时,首先将计算任务传输至基站,然后由MEC服务器执行计算任务。计算输入数据包括移动系统设置、程序代码和输入参数,计算结果通常比输入数据要小得多。因此,与许多研究类似,本文忽略MEC服务器将计算结果发回移动设备的能耗和时间开销,只分析了卸载至MEC服务器时的数据传输阶段和任务执行阶段。
根据式(2),数据传输阶段用户nj的时延如式(5)所示:
(5)
其中,tran表示传输阶段。
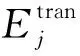
(6)
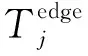
(7)

在上述卸载模型的基础上,nj执行其计算任务所需的总时间Tj如式(8)所示:
(8)
总能量消耗Ej如式(9)所示:
(9)
3 问题描述
移动边缘计算网络中,用户的QoS主要表现为任务的完成时间和能量消耗。基于上述系统模型,将用户nj的系统开销定义为时延和能耗的加权和,由于系统中时延和能耗的数值不在同一数量级,较大值会主导优化过程,本文引入λ为归一化因子对时延、能耗进行归一化处理[19]。将λ定义为处理所有任务的平均时延与平均能耗之比,即λ=Tj/Ej。则用户nj的系统开销Zj如式(10)所示:
(10)
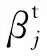
本文以最小化所有用户的系统开销为目标,构造了问题P1所表示的计算卸载和资源分配的联合优化问题,如式(11)所示:
s.t.C1:yj,i∈{0,1},
C3:fj,i≥0,i=1,2,…,S,j=1,2,…,K,
(11)
其中,在目标函数Z(Y,F)中,Y表示计算卸载决策的矩阵,F表示资源分配的矩阵。通过联合Y和F使总系统开销最小。约束C1 和C2表示每个用户任务只能选择在本地执行或最多卸载到一个服务器上执行;约束C3表示任务卸载被分配到的计算资源是非负的;C4表示分配给同一服务器卸载用户的总计算资源不能超过服务器可用的计算资源。
4 问题求解
问题P1包含2个待求解变量,即卸载决策(为整数变量和)和资源分配(为连续变量)。变量之间不仅类型不同,还存在较强的耦合关系,使得P1是一个具有NP-hard性质的MINLP问题,难以在多项式时间内求解。为了解决这个问题,本文将其分为计算资源分配和计算卸载决策2个子问题。
4.1 计算资源分配
计算资源分配问题只需考虑卸载到MEC服务器的用户任务。当卸载决策固定,即Y=Yo时,定义卸载至MEC服务器mi的用户集合Noff={nj|yj,i=1,i=1,2,…,S,j=1,2,…,K}。计算资源分配的目的是使任务在MEC服务器执行的时延最小化,并且只与约束C3和C4有关,所以问题P1可以转换为式(12):
s.t.C3,C4
(12)
将式(12)表示为h(F),计算关于fj,i的二阶偏导数,如式(13)和式(14)所示:
(13)
(14)
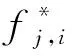
(15)
(16)
4.2 基于改进鲸鱼优化算法的卸载策略
当计算资源分配确定时,即F=Fo,问题P1转换成式(17):
s.t.C1,C2
(17)
智能优化算法是求解该问题的有效方法。鲸鱼优化算法WOA (Whale Optimization Algorithm)应用广泛、参数少且易于实现[20,21],但收敛速度慢,容易陷入局部最优。为了进一步平衡WOA在任务卸载过程中的局部开发能力和全局探索能力,提高收敛速度和精度,本文提出了一种改进的鲸鱼优化算法IWOA (Improved Whale Optimization Algorithm)来求解卸载决策Y。
4.2.1 种群初始化及编码

Xl(t)=randn(Num,K×(S+1))
(18)
其中,randn(Num,K×(S+1))表示随机产生的一个Num×(K×(S+1))的均值为0、方差为1的标准正态分布矩阵。然后按照X1l(n,m)=Xl((S+1)×(n-1)+m)对Xl(t)中的元素进行选取,得到一个K×(S+1)的矩阵X1l,其中,n=1,2,…,K,m=1,2,…,S+1。然后,将矩阵X1l中每行最大的值改为1,其余改为0,则得到一个满足约束的卸载矩阵Y。
如图2所示,假设当前系统中用户数K为3,MEC服务器数S为2,鲸鱼种群数Num为2。鲸鱼种群初始化后进行编码得到对应的卸载决策矩阵。图2中的卸载决策Y表示用户n1将任务卸载至MEC服务器m1,用户n2进行本地计算(即m3),用户n3将任务卸载至MEC服务器m2。
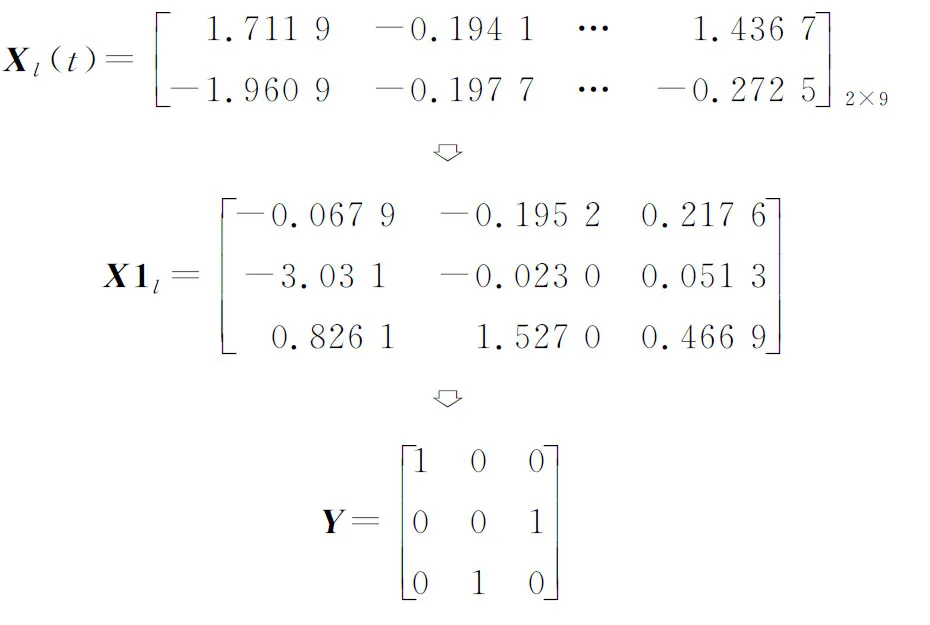
Figure 2 Code example
4.2.2 适应度函数
适应度函数用来评估解的可行性。WOA适用于解决最小化问题,式(17)为最小化问题,因此式(17)不需要修改,适应度函数如式(19)所示:
Fitness(Y)=Z(Y,Fo)
(19)
4.2.3 种群更新
(1) 非线性收敛因子。
WOA根据鲸鱼的进食过程建立了3个数学模型:包围猎物、泡网攻击法和寻找猎物。首先,WOA以当前最优解作为目标猎物,以离猎物最近的鲸鱼作为最佳搜索代理。然后,其他个体鲸鱼会接近目标猎物,并逐渐更新它们的位置。这种行为可表示为式(20)和式(21):
D=|C·X*(t)-X(t)|
(20)
X(t+1)=X*(t)-A·D·I
(21)
其中,D表示搜索代理到目标猎物的距离;I为单位向量;t为当前迭代次数;X*为局部最优解;C、A为系数,分别表示为式(22)和式(23)所示:
C=2·r
(22)
A=2a·r-a
(23)
其中,r是[0,1]的随机数,A取值依赖于a,a值随迭代次数的增加从2线性下降到0,即a=2-2t/tmax,tmax表示最大迭代次数。距离控制系数A决定了WOA的探索和开发,当|A|≤1时,算法进行开发阶段,其中,当[0,1]的随机数p<0.5时,进行包围捕食,p≥0.5时,进行泡网攻击法,如式(24)所示:
(24)
其中,D′=|X*(t)-X(t)|表示当前鲸鱼位置与猎物之间的距离,l′为[-1,1]的随机数,b为定义对数螺旋形状的常数。
当系数|A|>1时算法进行探索阶段,即寻找猎物,如式(25)所示:
X(t+1)=Xrand-A·D·I
(25)
其中,Xrand表示通过随机选择的鲸鱼在当前鲸鱼种群中的位置。
然而,WOA的真实搜索过程是非线性的,甚至更加复杂。这种线性下降可能带来2个问题:①在早期迭代过程中,包围猎物的行为更新较慢,收敛速度较低。如果全局最优值出现在早期迭代中,搜索的精度将受到很大的影响;②当接近最优值时,局部收敛速度会变慢。因此,本文根据不同初等函数的函数性质和图像特征,采用了基于指数函数的非线性收敛因子,数学表达式如式(26)所示:
(26)
其中,η,k是影响算法开发和搜索能力的因子。经过多次实验,η和k分别取值为10和6,会以更大的概率出现|A|≤1,鲸鱼种群包围猎物概率也更大,收敛速度也更快。
(2)自适应惯性权重。
改进的基于非线性收敛因子的新策略在一定程度上提高了算法的性能。然而,在使用新策略时,仅靠收敛因子无法平衡群体的全局探索能力和局部开发能力。受PSO启发,添加惯性权重并结合收敛因子来调整种群的全局探索能力和局部开发能力;并对原惯性权重的线性调整进行了改进,提出了一种新的自适应惯性权重更新策略,如式(27)所示:
(27)
其中,f(Pnbest)和f(Plbest)表示第t迭代时最佳位置的适应度值和局部最佳位置的适应度值,本文设置自适应惯性权重中的最大惯性权重wmax=0.9,最小惯性权重wmin=0.4[22]。
在加入自适应惯性权重更新策略后,将收缩包围和螺旋更新机制分别更新为式(28)和式(29):
X(t+1)=w·X*(t)-A·D·T
(28)
X(t+1)=w·X*(t)+D′ebl′cos(2πl′)
(29)
惯性权重w和非线性因子a都加快了收敛速度,但两者有着本质区别。a通过增加种群包围猎物的概率来提高收敛速度。w通过改变鲸鱼更新位置X*(t)所占的比例,随着迭代次数的增加,当目标函数值收敛到局部最优时,惯性权重增大;当目标函数值分散时,惯性权重减小;当目标函数值优于平均值时,惯性权重减小,以保留当前鲸鱼;当目标函数值低于平均值时,惯性权重增大,从而向较好的搜索区域靠拢。
(3) 反馈机制。
在WOA中,随着迭代次数增加,鲸鱼种群向当前最接近猎物的鲸鱼位置靠拢,导致多样性降低。因此,容易陷入局部最优位置。为了跳出局部最优,本文根据人工蜂群算法引入了反馈机制[23]。如文献[23]所述,如果在一定的迭代次数内最优解不变,为了跳出局部最优解,所有个体被再次随机放置,并继续迭代。按照上述思路对WOA进行修改,若X*(t)在20次迭代中没有变化,将随机选取的一半鲸鱼再次随机放置,剩下的鲸鱼不变化;如果X*(t)发生变化,则继续执行IWOA。
综上所述,IWOA的步骤描述如下:
步骤1初始化鲸鱼种群和所需的参数a、l′、tmax等,并将种群映射为卸载矩阵;
步骤2根据式(19)计算每个鲸鱼个体的适应度值,根据最小适应度准则,获得当前最优解;
步骤3分别通过式(26)和式(27)更新改进参数a和wt,随机生成参数p,并计算|A|;
步骤4当参数|A|≤1时,通过判断p是否大于0.5执行式(28)包围猎物或式(29)泡网攻击法更新当前鲸鱼的位置,否则当|A|>1时根据式(25)执行寻找猎物机制更新当前鲸鱼的位置;
步骤5计算每个个体的适应度值,如果存在最佳值,则更新鲸鱼的最优位置以及目标函数值;
步骤6若最优解在20次迭代中没有变化,执行反馈机制;
步骤7迭代次数加1,当达到最大迭代次数tmax时,停止迭代循环;
步骤8输出最优位置和适应度值。
4.3 资源分配与计算卸载决策的联合优化
如上所述,本文所提出的算法在每次迭代中采用IWOA求解卸载决策,然后根据给定的卸载决策,采用拉格朗日乘子法得到相应的计算资源最优分配,其中一个最优解作为输入,参与另一个求解过程,在对解进行多次迭代后,可以得到原优化问题稳定收敛的最优解,如算法1所示。

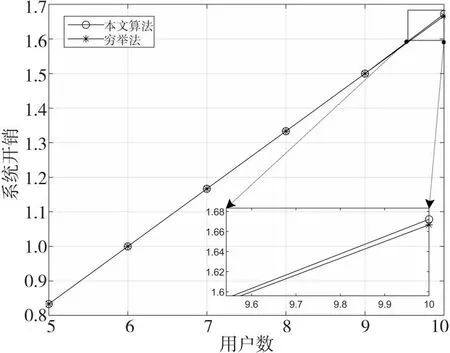
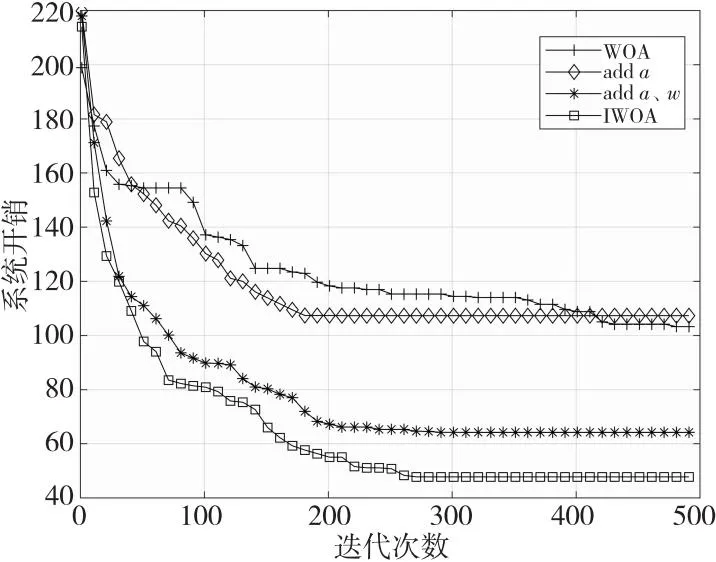
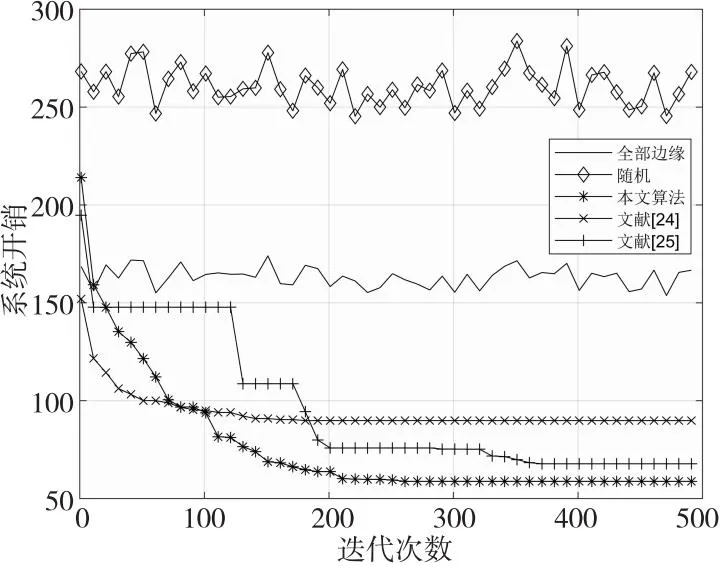
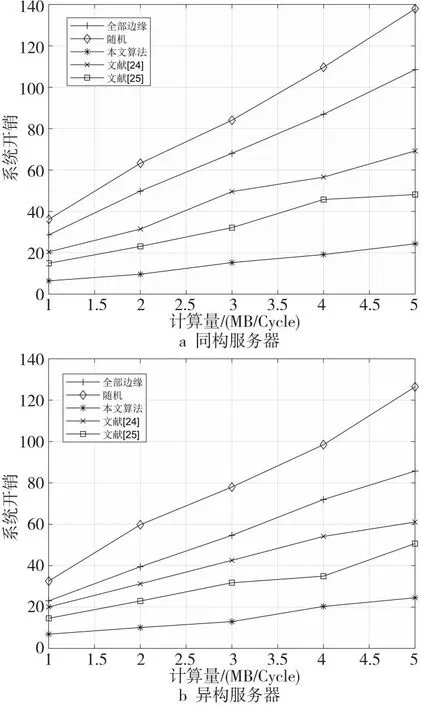
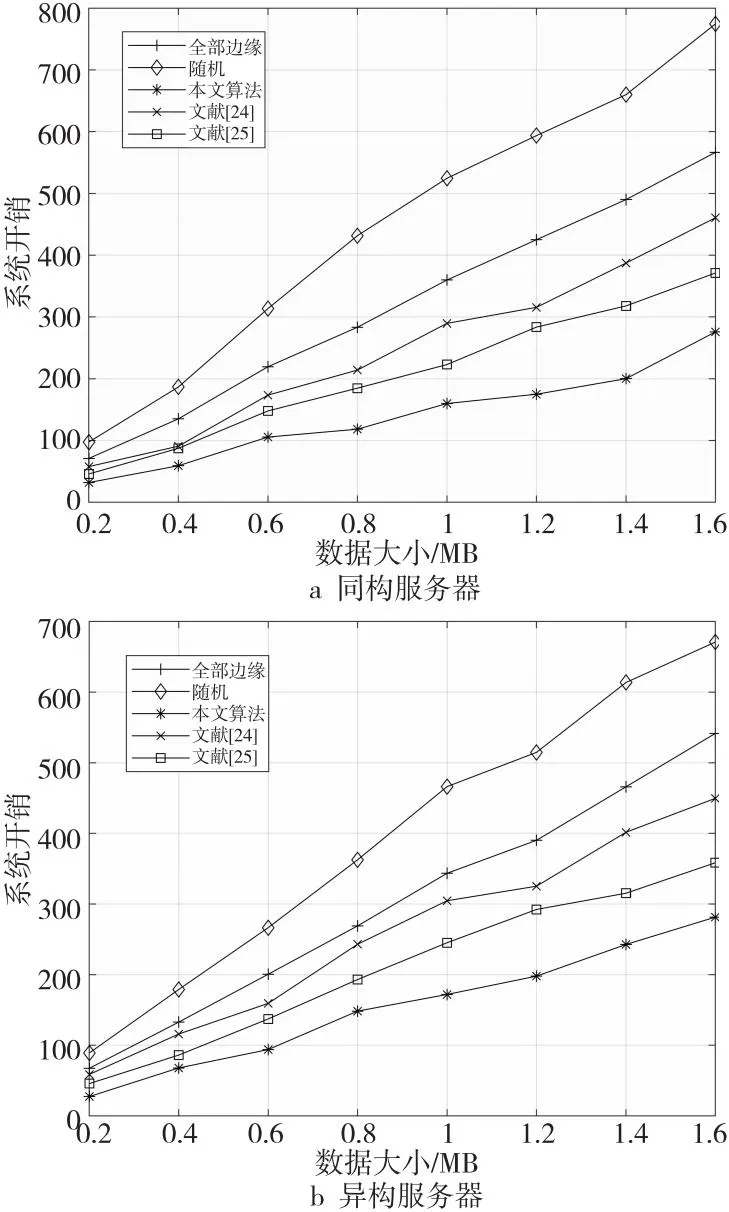
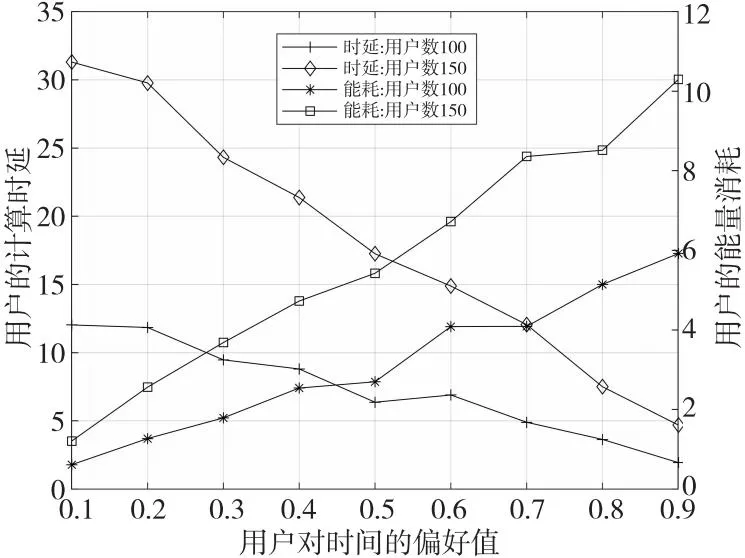
算法1 基于鲸鱼优化算法的联合资源分配和计算卸载算法输入:鲸鱼种群数Num、最大迭代次数tmax和相关参数。输出:计算资源分配解、卸载决策以及问题P1的最优目标函数值Z(Y*,F*)=Z*(t1)。1.初始化:迭代次数t=0、每个种群的鲸鱼位置、最大适应度值Z(t)=+∞;2.While (t 当达到最大迭代次数时,联合优化算法输出最优的卸载决策Y*、相应的最优计算资源分配解F*以及最小系统开销解Z(Y*,F*)=Z*(tmax)。其中,求解计算资源分配问题时,在每次迭代中需执行|S·Noff|次操作。在IWOA中,鲸鱼种群为Num,鲸鱼个体的维度为d=K×(S+1),最大迭代次数为tmax,IWOA复杂度为O(Num·d·tmax)。因此,本文联合优化算法复杂度为O((Num·d+|S·Noff|)·tmax)。 为了验证本文提出的联合优化算法的有效性,在Intel®CoreTMi5-7300HQ,CPU@ 2.50 GHz,16.0 GB RAM的实验配置,以及MATLAB R2020b的实验环境中进行了仿真实验。 将通信场景设置为一个1000 m×1000 m的矩形区域,有10个MEC服务器均匀分布在该区域,100个用户随机分布在该区域。相邻基站之间的间隔为100 m。将系统带宽B设为20 MHz,背景噪声方差N0设为-130 dBm,发射功率pn设为1 W。上行链路信道增益通过与距离相关的路径损耗模型产生,信道增益模型为h=140.7+36.7×lgdis,其中,dis是以km为单位的用户设备与基站之间的距离。 (1)随机卸载方案:用户将任务随机卸载至本地计算或任意一个MEC服务器上。 (2)全部边缘计算方案:所有用户选择将任务卸载至距离最近的MEC服务器上。 (3)文献[24]中采用的基于灰狼优化GWO(Grey Wolf Optimization)算法和WOA优化的混合方法。 (4)文献[25]中的双层优化方法:上层通过改进的蚁群算法求解,下层优化问题采用单调优化方法求解。 5.2.1 与穷举法的性能比较 为了衡量本文所提算法的有效性,本节将其与穷举法进行比较。穷举法通过遍历、比较所有可行解得到优化问题的全局最优解,但算法的复杂度会随着问题规模的增加呈指数级增加。本文由K个用户和S个服务器组成的系统中,每个用户可以选择在本地执行或者卸载到一个服务器上,这种情况下穷举法有(S+1)K种可行解,复杂度比较高,因此使用穷举法求解本文中存在大量变量的问题会导致非常长的运行时间。所以,本文在一个存在2个MEC服务器,移动设备数量为5~10的小规模网络场景中进行比较。 图3给出了分别应用本文算法与穷举法的系统开销,可以明显看出,本文算法的系统开销和穷举法的系统开销非常接近,随着用户数的增加系统开销都在穷举算法的1%以内,可见本文的联合优化算法是切实可行的。 Figure 3 System overhead comparison of the proposed algorithm and exhaustive method图3 与穷举法的系统开销比较 Figure 4 Comparison of Running time comparison of the proposed algorithm and exhaustive method图4 与穷举法的运行时间比较 图4给出了本文所提算法和穷举法的运行时间随用户数量变化的情况。从图4可以看出,虽然本文所提算法在最初的执行时间比穷举法的长,但随着用户数量的增加,穷举法的执行时间迅速超过本文所提算法的执行时间。由于本文所提算法的运行时间是线性增加的,而穷举法的运行时间是呈指数增长的,因此在大规模网络中应用本文所提算法可以显著减少任务卸载过程执行的时间,提高执行效率。 5.2.2 WOA改进策略对性能的影响 为了分析WOA的改进策略对结果的影响,在WOA中逐步加入本文所提出的方案。首先加入非线性收敛因子a,然后加入自适应权重系数w,最后加入反馈系统即IWOA。其收敛曲线如图5所示。 从图5中可以看出,WOA在加入非线性收敛因子a后,收敛速度有所提高,这是由于非线性收敛因子随着迭代次数的增加而减小得更快,从而种群也收敛得更快,但是它的准确性并没有太明显的提高;当同时加入非线性收敛因子和自适应权重系数时,收敛速度和精度都有显著提高;最后,采用反馈系统的IWOA相比WOA减小了53.7%的系统开销,在计算精度上也得到了进一步提高,这是因为反馈机制的加入增加了整个算法种群的多样性,使算法更容易跳出局部最优。可见,本文的改进策略是有效的。 Figure 5 Impact of IWOA improved strategy on system overhead图5 IWOA改进策略对系统开销的影响 5.2.3 收敛性分析 图6给出了系统开销随算法迭代次数增加的变化趋势。由于任务在选择随机卸载或全部边缘卸载时不受迭代次数的影响,因此解空间较大,且运行结果呈现随机性波动,但任务卸载至边缘时,计算资源会更丰富,系统开销比随机卸载的小38.5%左右。文献[24]和文献[25]均使用与本文算法相同的编码方式,系统开销都随着迭代次数的增加而减小,最终收敛到最优值。在收敛速度方面,文献[24]结合了GWO和WOA,收敛速度较快,以最少的迭代次数收敛到最终解,但其最终解是最差的;本文则在300次迭代之后才接近全局最优解,收敛性略差;文献[25]由于无法避免陷入局部最优,曲线剧烈波动,多次陷入局部最优值。在全局搜索能力方面,本文算法全局搜索能力最强,能够收敛到高质量的解,当迭代次数为300时,本文算法求得最优解的系统开销最小,分别比文献[24]和文献[25]的系统开销减小了34.5%和13.1%。 Figure 6 Effect of number of iterations on system overhead图6 迭代次数对系统开销的影响 5.2.4 用户数量的影响 图7为用户数从 50增加到300时,系统开销的变化情况。所有算法的系统开销都随着用户数的增加而增加。从卸载模型中分析,这是因为系统开销与时延、能耗呈线性相关的关系,当用户总数增加时,任务量增加,处理任务的总时延和总能耗也增加。在初始用户数量较小时,各个方案的系统开销相近,因为此时计算资源充足,使得开销差异不明显。随着用户数的增加,差异越来越大,这是因为在用户数较多时,对资源的需求也随着增加,然而系统中可用的计算资源总量保持不变,分配给每个任务的计算资源量将逐渐减少,用户无法选择合理的卸载位置,导致可使用的计算资源较少,系统计算开销更大。当用户超过系统容量时,多余的用户只能在本地执行,系统开销增长速度更快。 Figure 7 Impact of number of users on system overhead图7 用户数量对系统开销的影响 随机卸载的增长速度最快,性能是所有方案中最差的,说明了用户选择适当任务卸载决策的重要性。本文算法在收敛性和稳定性方面都优于其他算法的,能够充分利用移动设备和MEC服务器上的可用资源,是5种方案中性能最好的,且更适合用于设备较多的场景。当用户数为300时,本文算法的系统开销分别比文献[24]的、文献[25]的、全部边缘的和随机卸载的降低了18.1%,9.4%,32.1%和44.6%。随着MEC环境的变化,本文算法能够不断调整卸载策略以获得最优解,因为增加了反馈机制,提高了种群多样性,减少了陷入局部最优的可能性;利用非线性收敛因子和惯性权重系数改进鲸鱼个体位置更新,提高了收敛速度和精度。 5.2.5 任务属性对系统开销的影响 本文还比较了计算任务在不同的输入数据大小和所需的任务工作量时的系统开销。考虑了MEC服务器的2种配置情况,其中,同构服务器的计算资源为fm=20 GHz,异构服务器的计算资源为fm=10 GHz,20 GHz,30 GHz。 图8展示了任务所需工作量对不同算法的系统开销的影响。可以看出,随着所需CPU周期数的增加,所有方案的系统开销都呈上升趋势。这是因为随着任务所需计算周期数的不断增加,用户需要更多的计算资源来处理任务,导致更大的时延和能耗,从而系统开销也随着增加。从曲线变化的程度可以看出,在同一任务所需工作量的情况下,本文算法能够实现最小的系统开销,且具有更好的稳定性,因为当本地用户设备有限的计算资源无法满足任务需求时能够选择最优的MEC服务器,这是影响系统开销的关键。 Figure 8 Impact of required task workload on system overhead图8 任务所需工作量对系统开销的影响 图9展示了任务的输入数据大小对系统开销的影响,输入数据大小的增加会导致任务在传输阶段的时延和能耗增加,从而导致任务在卸载过程中的系统开销增加。实验结果表明,数据量小、计算量大的卸载任务比数据量大、计算量小的任务可以获得更好的结果。此外,同构服务器设置中的所有方案的性能与异构服务器设置中差异微乎其微,说明本文提出的方案同样能够应用于不同的配置中。 Figure 9 Impact of the size of input data of the task on the system overhead图9 任务的输入数据大小对系统开销的影响 5.2.6 用户偏好的影响 图10展示了用户对时间的偏好值从0.1变化到0.9时用户时延和能耗的变化情况,同时对比了用户数为100和150时的情况。可以看出,平均时间消耗随着时间权重的增加而减少,且以更高的能量消耗为代价,不同用户数量受用户时延权重的影响曲线变化一致。 Figure 10 Impact of user latency weights on latency and energy consumption图10 用户时延权重对时延和能耗的影响 本文研究了多用户、多MEC服务器的计算卸载和资源分配,以最小化时延和能耗的加权和为目标,提出了一种联合资源分配和卸载决策优化策略。该策略由基于WOA的任务卸载决策算法和基于拉格朗日乘子法的计算资源分配算法组成,能够获得最优的卸载决策、最优分配的MEC服务器计算资源,本文的仿真结果证实了该算法的有效性及其相对于其他算法的优越性,能够有效降低系统中的计算开销。在未来工作中,将考虑任务之间的依赖性,进一步优化系统模型。5 实验仿真
5.1 仿真场景与参数设置
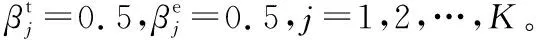
5.2 性能分析


6 结束语

