DRM:基于迭代归并策略的GPU并行SpMV存储格式*

王宇华,何俊飞,张宇琪,徐悦竹,崔环宇

(1.哈尔滨工程大学计算机科学与技术学院,黑龙江 哈尔滨 150001; 2.电子政务建模仿真国家工程实验室,黑龙江 哈尔滨 150001)

1 引言

在科学计算和工程应用领域中,稀疏矩阵向量乘法SpMV(Sparse Matrix-Vector multiplication)被广泛应用于流体力学[1,2]、结构力学[3]、空气动力学[4]、分子动力学[5]和天体物理学[6]等领域。特别地,在利用迭代法求解线性系统的过程中,SpMV往往占据了高达60%～70%的计算量[7]。因此,对SpMV及其优化的研究对于加速科学计算具有重要的意义,这也使其成为高性能计算领域的研究热点之一。

大多数SpMV过程形如:y=Ax。其中A表示稀疏矩阵,x是输入向量,y是输出向量。矩阵的稀疏性导致SpMV运算效率低下,SpMV的性能高度依赖于矩阵的非零元分布,非零元分布决定了其内存访问模式,并且不同矩阵之间有很大的差异。稀疏对角矩阵是一类特殊的稀疏矩阵,其非零元素按照对角线的形式密集排列。针对该特殊的结构,Bell等人[8,9]首次将DIA(DIAgonal)格式应用到了GPU平台上,并通过实验证明了DIA更适合于稀疏对角矩阵。DIA按照矩阵中的对角线来进行存储,一个对角线利用一个偏移量进行索引,相比于其他格式,这样不仅能够减少列索引的存储,同时还具有良好的时间空间局部性和访问向量的连续性。但是,当矩阵中存在散点和长断行时,DIA格式会出现零填充现象[10],在运算时会造成空间和计算资源的浪费,最终导致空间和时间的利用率下降。

近年来,很多研究人员提出了不同的改进格式,如CRSD(Compressed Row Segment Diagonal)[11,12]、DDD-SPLIT(Direct Dense Diagonal SPLIT)[13]、 HDIA(Hacked DIAgonal)[14]、IHYB(Improved HYB format)[15]和DIA-Adaptive (DIAgonal-Adaptive)[16]等。其中,大多数格式是通过对矩阵进行分块来解决零填充问题,虽然使SpMV性能有所提升,但由于稀疏矩阵中非零元分布不规则,块间非零元个数存在一定差异,会出现块间负载不平衡的问题。

负载不平衡会引起多个线程的空闲等待,浪费了计算资源的同时降低了运算的并行性,会对最终的运算效率产生较大的影响。因此,本文提出了一种新的存储格式DRM(Divide-Rearrange &Merge)。该格式利用基于固定阈值的矩阵划分策略和基于迭代归并的矩阵重构策略,对稀疏矩阵进行划分,并对划分结果进行迭代归并,在解决零填充问题的同时达到了负载平衡的目的。

2 相关工作

目前,国内外很多研究人员对稀疏矩阵向量乘进行了广泛的研究,提出了一系列优化方法,针对不同问题的优化主要分为2类:最小化零填充量和负载平衡。

2.1 最小化零填充量

Choi等人[17]提出了BCSR(Blocked Compressed Sparse Row)和BELL(Blocked ELLpack)存储格式,通过对矩阵进行分块处理,提高了SpMV的性能,但会出现块间负载不平衡的问题。Yuan等人[13]提出了DDD-SPLIT格式,利用对角线将稀疏矩阵分成若干子块,压缩对角线上连续的相同元素,进而压缩具有相同值的子块,节省了大量的存储空间。Barbieri等人[14]提出了HDIA格式,通过将原始矩阵分成大小相等的行组,并将行组以DIA格式存储,减少了零元素的填充量和缓解了缓存未命中的问题。但是,该格式可能会出现块间元素数量差异过大的现象。Gao等人[16]提出了DIA-Adaptive格式,将矩阵分为3种类型,并自适应地选择DIA、BRCSD-Ⅰ(Diagonal Compressed Storage based on Row-Blocks-Ⅰ)、BRCSD-Ⅱ格式中的一种对矩阵进行存储,改善了稀疏对角矩阵存在长偏移、散点和长断行时的零填充问题,然而这样可能会出现负载不平衡的问题。Sun等人[11,12]提出了CRSD存储格式,通过设计对角线格式,将矩阵的对角线分成不同的组,并在行方向上将矩阵划分成行片段,解决了稀疏对角矩阵存在散点和长断行时的零填充问题。但是,由于不同对角线格式中对角线的数量不一致,该格式会出现行片段间负载不平衡的问题。Yang等人[18,19]提出了一种混合存储格式HDC(Hybrid of DIA and CSR(Compressed Sparse Row)),通过设定分割阈值,将矩阵分为对角区域和离散区域,并分别采用DIA格式和CSR格式进行存储,有效地减少了矩阵存储时的零填充量。但是,并行SpMV运算性能受分割阈值影响较大,最佳阈值又难以确定。

2.2 负载平衡

Liu等人[20]提出了CSR5格式,通过将非零元均匀地划分为多个相同大小的2D切片,让一个SIMD(Single Instruction Multiple Data)通道处理切片的一列,使稀疏矩阵达到近乎最佳的负载平衡。但是,从CSR到CSR5的预处理时间需要比SpMV的多10～30倍。Yang等人[21]提出了一种基于非零元分布的最优分块策略和一种重排序算法,并利用混合格式BCE(Blocked stored format mixed CSR and ELL)对矩阵进行压缩存储,在提升SpMV性能的同时,解决了分区后的负载平衡问题。Cui等人[22]提出了一种自动获取最优块划分的策略和一种基于分块策略的矩阵重排方法,并采用PBC(Partition-Block-CSR)格式来存储重排序后的矩阵,分块策略和矩阵重排保证了分块之间的标准差最小,既满足了负载均衡条件,又避免了零元素填充,有效提高了并行计算效率,但是该方法存在预处理时间过长的问题。Bian等人[23]提出了CSR2(Compressed Sparse Row 2)存储格式,它可以根据矩阵的特点自动确定单次执行的矩阵分块宽度,并借助SIMD函数在平台上充分发挥SIMD向量化的效率。与CSR5相比,CSR2具有更少的存储空间消耗和更低的格式转换开销。Gao等人[24]提出了AMF-CSR(Adaptive Multi-row Folding of CSR)存储格式,通过对多个非零行进行折叠,并合并非零数量相近的行,增加了行中非零元的密度,提升了x向量的访问局部性,改善了线程块间负载不均衡的问题。但是,部分阈值根据经验设置,可能存在最后一块与其他块的非零元数量不平衡的现象。

从以上分析可知,目前,针对稀疏对角矩阵的主流存储格式虽然能够在一定程度上提升并行SpMV效率,但仍然会出现零填充过度和GPU线程块间负载不平衡的问题。

3 稀疏矩阵存储格式介绍

3.1 DIA存储格式

DIA存储格式是处理稀疏对角矩阵的一种经典格式。对于具有k条对角线的n维稀疏矩阵,该格式用2个数组来存储矩阵,一个是大小为k×n的data数组,用来存储每条对角线的元素;另一个是大小为k的offsets数组,用来存储每条对角线相对于主对角线的偏移量。稀疏矩阵示例和DIA存储格式如图1所示,其中Ci和Ri表示稀疏矩阵的列向量和行向量。

DIA格式适合存储存在密集对角线的稀疏对角矩阵。若矩阵中存在散点、长断行和与主对角线偏移较大的对角线时,会填充大量的零元素,这在浪费存储空间的同时还会影响GPU上SpMV的运算效率和时间性能。

a 稀疏矩阵

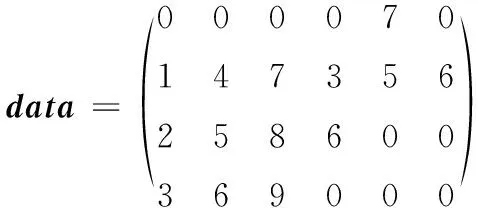
offsets=[-3,0,1,3]

3.2 HDIA存储格式

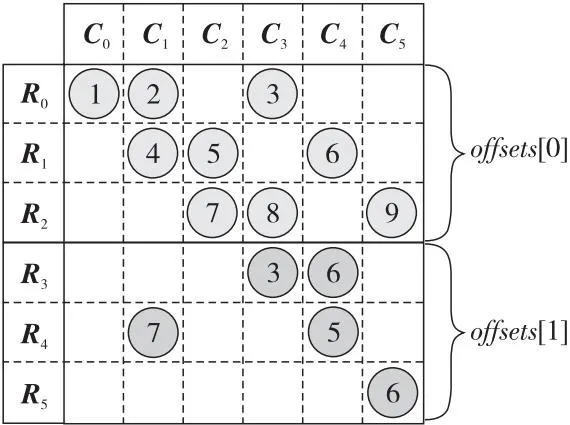
HDIA存储格式是在DIA格式的基础上加入了分块的思想。通过设置固定的行块大小,将稀疏矩阵划分为大小相等的行块,并对每一行块采用DIA格式进行存储。该格式利用3个数组存储矩阵,hackOffsets数组用于存储每个行块的对角线个数,hdi_offsets数组用于存储每个行块中对角线的偏移量,hdi_data数组用于存储每个行块中的元素。对于图1中的矩阵A,当行块大小设置为2时,HDIA存储格式如图2所示,其中bi表示矩阵划分后的行块。

hackOffsets=[0,3,6,8]

HDIA存储格式有效地解决了矩阵中存在长断行和散点时的零填充问题,但由于每个块中非零元个数不一样,甚至差异很大,可能会导致块间的负载不平衡,从而影响并行SpMV的性能。

3.3 DIA-Adaptive存储格式

DIA-Adaptive是一种自适应存储格式。首先通过稀疏矩阵的特征对矩阵进行类别判断,然后根据矩阵的类别对矩阵采用DIA、BRCSD-Ⅰ、BRCSD-Ⅱ中的一种格式进行压缩存储。其中,BRCSD-Ⅰ格式利用矩阵的偏移量和一种计算策略来获得矩阵的有效片点和交叉片点,利用交叉片点对矩阵进行分块。采用2个数组存储矩阵,brcsdⅠ_offsets数组用于存储每个块的起始行号和块内对角线的偏移量,brcsdⅠ_data数组用于存储每个块的元素。对于图1中的矩阵A,BRCSD-Ⅰ存储格式如图3所示,其中offsets[i]表示对矩阵该部分的偏移量进行统一存储。

brcsdⅠ_offsets={0|[0,1,3],3|[-3,0,1]}

BRCSD-Ⅱ格式通过设置固定的nrows值,将矩阵分成大小相等的行块,并利用一定的合并策略将具有相同偏移量的块进行偏移量压缩。采用2个数组存储矩阵,brcsdⅡ_offsets数组用于存储相同偏移量的块数和对应的偏移量,brcsdⅡ_data数组用于存储每个块的元素。对于图1中的矩阵A,nrows=2时的BRCSD-Ⅱ存储格式如图4所示。

brcsdⅡ_offsets={2|[0,1,3],1|[-3,0]}

BRCSD-Ⅰ存储格式有效解决了矩阵存在长偏移时的零填充问题,但由于每块行数不一致,可能会存在块间负载不平衡现象。BRCSD-Ⅱ存储格式有效解决了矩阵存在散点和长断行时的零填充问题,虽然每块行数相等,但仍可能存在块间负载不平衡的现象。

4 DRM格式以及并行SpMV实现

针对稀疏对角矩阵存储时的零填充问题以及现有分块格式存在的负载不平衡问题,本文提出了一种DRM存储格式。该格式利用基于固定阈值的矩阵划分策略和基于迭代归并的矩阵重构策略,将输入矩阵划分为大小相等的行段,对行段进行迭代归并,旨在减少矩阵存储时的零填充量,实现子块间负载平衡,提升SpMV在GPU上的并行效率。

4.1 基于固定阈值的矩阵划分策略

DIA存储格式适合存储对角线密集的稀疏矩阵,但是在实际工程计算问题中得到的稀疏对角矩阵往往存在一些散点和长断行。若直接采用DIA格式进行存储,会出现零填充问题,当矩阵维数较大时,填充的零元素个数甚至会远超非零元素的个数,这样不仅浪费内存空间,还会严重影响DIA格式的时间性能。因此,DRM存储格式首先对稀疏对角矩阵进行一次固定阈值(nrows)的划分,使对角线按行段进行存储,这样就有效解决了矩阵存储时的零填充问题。为了说明划分的重要性,本文进行了深入分析。

定义1假设稀疏矩阵B分为K块,每个块表示为B0,B1,B2,…,BK-1,若块之间满足式(1)和式(2),则称Bi为稀疏矩阵B的子块:

Bi∩Bj=∅,i,j=0,1,…,K-1,i≠j

(1)

(2)

定义2假设子块Bi由若干小块组成,每个小块表示为bi0,bi1,bi2,…,若小块之间满足式(3)和式(4),则称bij为行段:

bij∩bik=∅,j≠k

(3)

(4)

定义3对一个N维的稀疏对角矩阵,以nrows为行段大小对矩阵进行划分,矩阵所分的行段数如式(5)所示,行段中的操作数个数如式(6)所示:

bl=N/nrows

(5)

opeh=digh×nrows,h=0,1,…,bl-1

(6)

其中,bl为矩阵所分的行段数,opeh为行段中的操作数个数,digh为行段中的对角线个数。操作数是矩阵进行SpMV运算时需要参与运算的元素个数。由于矩阵存储时的零填充问题,除了非零元外,一部分零元素也会参与运算,同样属于操作数。

定义4对定义3中的矩阵,若矩阵包含S条对角线,DIA格式压缩矩阵时,需要存储的操作数个数如式(7)所示:

opeDIA=S×N

(7)

以nrows为行段大小对矩阵进行划分,划分后需要存储的操作数个数如式(8)所示:

h=0,1,…,bl-1,digh≤S

(8)

其中,opeDRM满足式(9):

nrows∈{1,2,…,N/2}

(9)

由式(9)可知,无论nrows为何值,都满足opeDRM≤opeDIA。假设矩阵B在定义4的基础上存在一个散点,则操作数个数的变化如式(10)和式(11)所示:

opeDIA=(S+1)×N

(10)

S×N+nrows

(11)

由式(10)和式(11)可推出式(12):

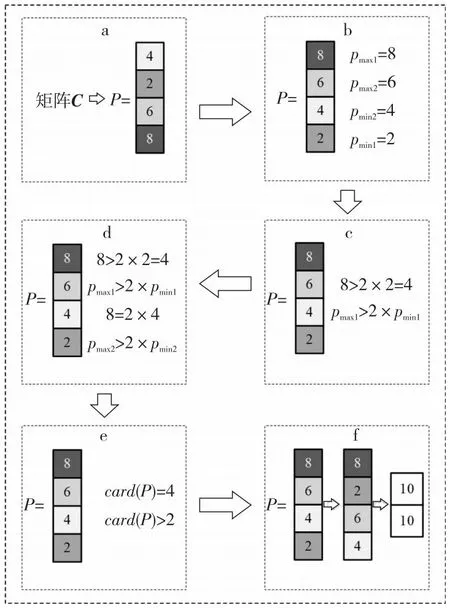
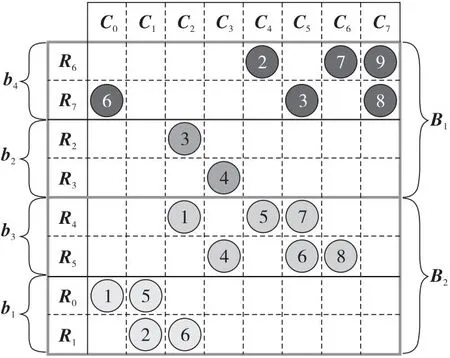
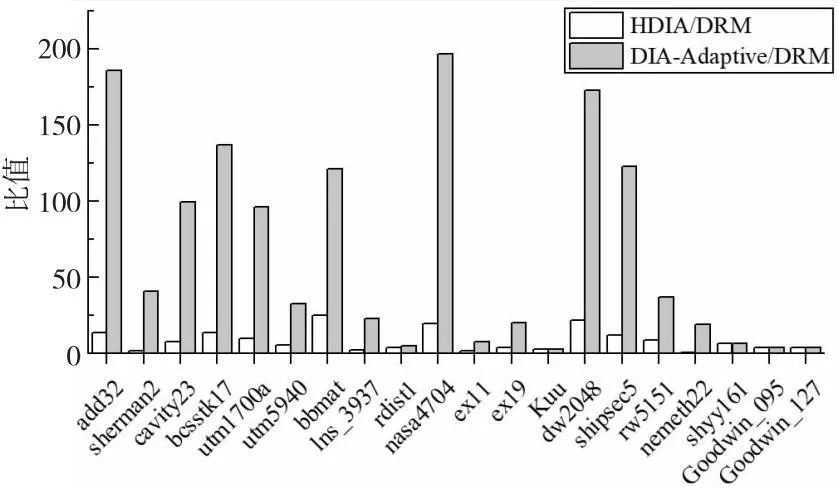
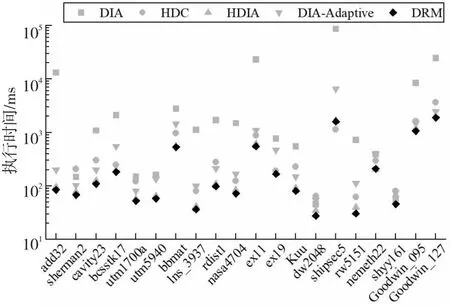
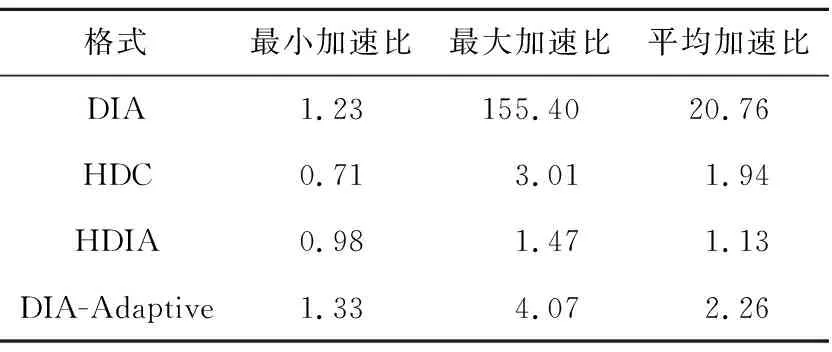
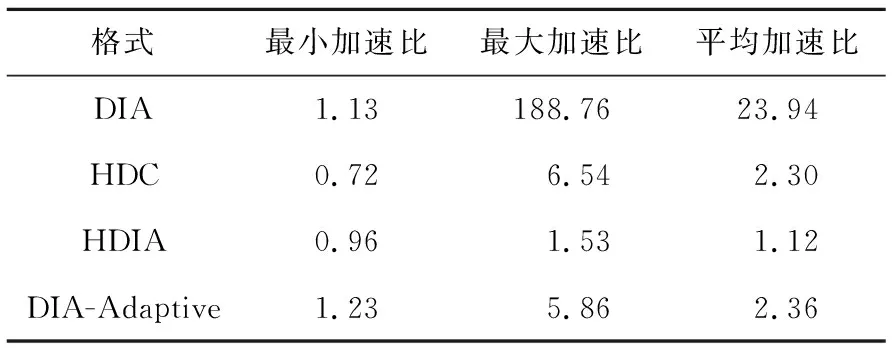
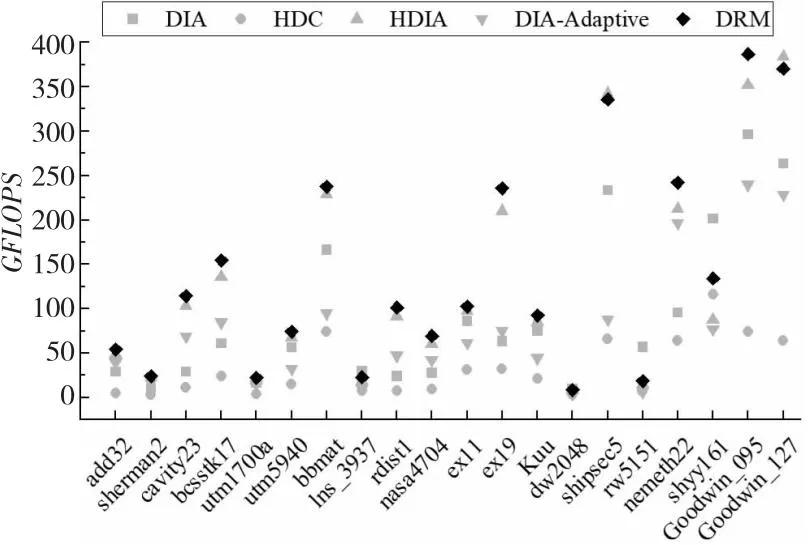
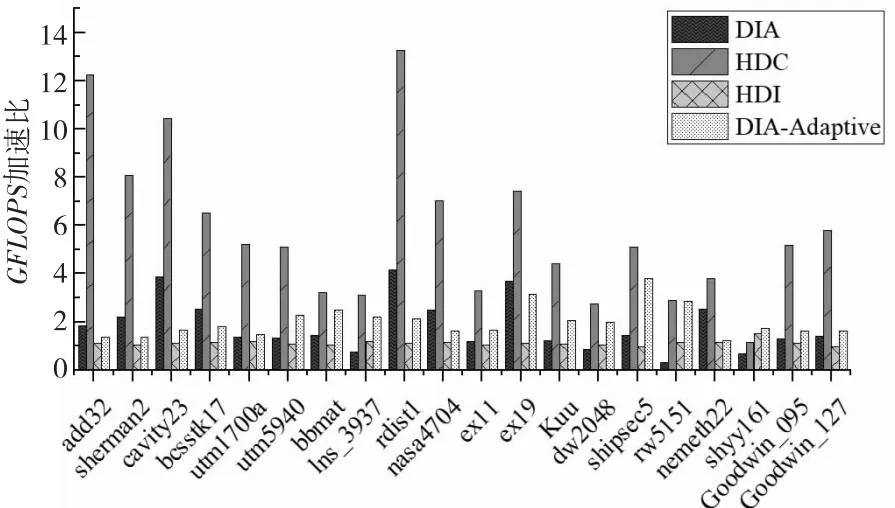
opeDRM

(12)

因此,当稀疏矩阵中存在散点或长断行时,相比DIA存储格式,对矩阵的划分一定能减少矩阵存储时的零填充量。对于存在散点或长断行较多的矩阵,通过划分减少的零元素填充更多。

以图5的稀疏矩阵B为例,当直接使用DIA格式存储该矩阵时,opeDIA=32,填充了14个零元素。若先使用划分策略对矩阵进行划分,当nrows=4时,bl=2,opeDRM=24,需要填充6个零元素;当nrows=2时,bl=4,opeDRM=20,只需要填充2个零元素。因此,对稀疏矩阵进行一次固定阈值的划分是必要的,能有效减少矩阵存储时的零填充量。nrows=2时矩阵划分结果如图6所示,本文称图6中的矩阵为矩阵C。

Figure 5 Example of sparse matrix B图5 稀疏矩阵B示例

Figure 6 Partition results of the matrix when nrows is 2图6 nrows=2时矩阵的划分结果

本文以nrows=2为例进行说明,但实验时的nrows固定为32。首先,在GPU架构中线程调度的基本单位是warp,一个warp包含32个线程,若同一warp内的线程访存地址一致或相邻,可以减少线程的访存时间,从而提升SpMV的性能。其次,本文针对nrows进行了大量的测试和实验,发现nrows的大小和SpMV性能成反比,但随着nrows的减小,预处理时间会逐渐增大。因此,为了达到一个较好的性能平衡,将nrows固定为32。

4.2 基于迭代归并的矩阵重构策略

对稀疏对角矩阵进行一次固定阈值的划分后,减少了矩阵存储时的零填充量,但由于行段间的操作数个数不一致,很容易出现GPU线程块间负载不平衡的问题。针对此问题,本节提出了一种基于迭代归并的矩阵重构策略,先将矩阵划分的行段按照操作数个数进行重新排列,再根据排列结果将对应行段迭代归并成子块,实现了子块间的方差最小化,满足了并行SpMV运算时负载平衡的条件。

定义5对稀疏对角矩阵进行一次固定阈值的划分后,行段间操作数个数的方差如式(13)所示:

(13)

其中,ave是行段中操作数个数的平均值,bl是矩阵以nrows为阈值进行划分后的总行段数,var是行段间操作数个数的方差。方差是衡量一组数据平衡与否的标准,方差越小,说明数据间的差异越小。矩阵划分后,每个行段中操作数个数的大小是否相似,决定了并行SpMV运算时矩阵的负载是否平衡。

负载不平衡会导致线程发散,引起计算资源的浪费,同时还会影响GPU上并行SpMV的计算速度,降低整个计算过程的效率。因此,DRM格式使用基于迭代归并的矩阵重构策略,对矩阵划分后的行段进行迭代归并,能够有效实现GPU线程块间计算量的最大平衡。

定义6对一个集合P,假设P含有l个元素,即P={p0,p1,…,pl-1}。若pmax1、pmin1、pmax2和pmin2满足式(14)～式(17),则分别称为集合P中的最大值、最小值、次大值和次小值:

pmax1≥pr,r=0,1,…,l-1

(14)

pmin1≤pr,r=0,1,…,l-1

(15)

pmax1≥pmax2≥ps1,ps1∈(P-{pmax1})

(16)

pmin1≤pmin2≤ps2,ps2∈(P-{pmin1})

(17)

基于迭代归并的矩阵重构策略如下所示:

(1)构造操作数集合P。基于每个行段中对角线的个数digh和矩阵划分阈值nrows,利用式(6)计算每个行段中操作数个数opeh,并将其存入集合P。

(2)整理集合P。P中含有bl个元素,可表示为P={p0,p1,…,pbl-1},循环执行以下步骤:

①对集合P按照元素递减的顺序重排,重排后的P={pmax1,pmax2,…,pmin2,pmin1}。

②取出集合P中的最大值pmax1和最小值pmin1,如果满足pmax1>2×pmin1,则执行③。否则,结束循环,执行(3)。

③取出集合P中的次小值pmin2,如果满足pmax1>2×pmin2,则将最小值pmin1和次小值pmin2对应的行段进行归并,并将2个行段中的操作数个数相加,即psum=pmin1+pmin2,将psum存入集合P中。否则,结束循环,执行(3)。

(3)判断集合P中元素的总数card(P)是奇数还是偶数。若是奇数,则把最小值pmin1和次小值pmin2对应的行段进行归并,并将2个行段中的操作数个数之和存入集合P中,再根据递减顺序进行一次重排。若是偶数,直接执行(4)。

(4)判断card(P)是否满足card(P)>2,若满足,则按照最大值pmax1和最小值pmin1、次大值pmax2和次小值pmin2归并的方式,将集合P中每个值pr对应的行段归并为子块,得到最终的归并结果。否则,直接将集合P当作最终归并结果。

经过以上步骤后,每个子块的操作数个数将趋近于平衡,使子块间操作数个数的方差变小,从而实现了GPU线程块间的负载平衡。基于迭代归并的矩阵重构算法如算法1所示。

算法1 基于迭代归并的矩阵重构算法输入:稀疏矩阵B,分块阈值nrows。输出:重构后的操作数集合P。1:P ← Getoperands(B,nrows);2:sort(P.begin(),P.end(),descending);3:while pmax1> 2*pmin1 and pmax1> 2*pmin2do4: pmin2+=pmin1;5: P.pop_back();6: sort(P.begin(),P.end(),descending);7:end while8:int len = P.size();9:if len mod 2=0 then10: for r=0 → lendo11: if r < (len -1- r)then12: pr+=plen-1-r;13: P.pop_back();14: end if15: end for16:else17: plen-2+=plen-1;18: P.pop_back();19: sort(P.begin(),P.end(),descending);20: len=P.size();21: for r=0 → lendo22: if r < len -1- rthen23: pr+=plen-1-r;24: P.pop_back();25: end if26: end for27:end if

算法1的第1～2行计算矩阵划分后每个行段中的操作数个数,将其存入集合P,并对集合P中元素进行递减排序。第3～7行循环归并满足条件的行段。第8行统计集合P的大小,若为偶数(第9～15行),直接将集合P中对应的行段归并为子块;若为奇数(第16～27行),则先归并最后2个行段,并进行一次递减排序,再将剩余的行段归并为子块。

以矩阵C为例,行段迭代归并过程如图7所示。

Figure 7 Iterative merging process of line segments图7 行段迭代归并过程

首先利用式(6)计算每个行段中的操作数个数,并将其存入集合P。然后,对集合P进行递减排序,取出P中的最大值8和最小值2,由于8>2×2=4,满足循环执行步骤②,取出集合P的次小值4,由于8=2×4,不满足循环执行步骤③,则执行下一步。最后,判断card(P)是奇数还是偶数,由于card(P)=4,且大于2,则根据pr的大小,将集合P中的行段两两归并为子块,得到最终集合P={10,10}。

基于迭代归并的矩阵重构结果如图8所示,其中,B1和B2为最终归并的子块,每个子块含有2个行段。通过式(13)计算可知,子块间操作数个数的方差为0,表示稀疏矩阵已达到完全的负载平衡状态。此时,在GPU上进行SpMV运算时会有效平衡线程块间计算负载,提升运算的效率和性能。

Figure 8 Matrix reconstruction results based on iterative merging图8 基于迭代归并的矩阵重构结果

4.3 DRM存储格式

DRM存储格式首先基于固定阈值的矩阵划分策略,将矩阵划分为多个行段,再结合4.2节中的迭代归并策略,将多个行段归并为子块,最终实现子块间opei的最大均衡,有效解决了稀疏对角矩阵在并行SpMV运算时的零填充和负载不平衡问题。

在GPU上进行并行SpMV运算之前,需要将矩阵压缩的数据存储到数组中。因此,首先建立与计算相关的数组。数组drm_dnum以累加的方式存储子块中每个行段中的对角线个数,用于行段中操作数个数的计算。数组drm_index存储每个行段归并后的索引用于SpMV运算时矩阵行索引。数组drm_blo以累加的方式存储子块中包含的行段个数,用于对每个行段进行索引。数组drm_off和drm_val分别存储子块中每一行段内对角线的偏移量和元素值。

对图5中的矩阵B,利用上述5个数组存储的结果如图9所示。

Figure 9 DRM storage format representation of matrix B图9 矩阵B的DRM存储格式表示

4.4 基于DRM存储格式的并行SpMV算法

本文在4.2节中提供了一个矩阵重构策略,实现了GPU线程块间计算量的最大相似性,在本节进一步提出一种新的基于DRM存储格式的并行SpMV算法。由于DRM将稀疏对角矩阵划分为行段,并对行段进行了迭代归并,导致子块间的行段是乱序排列的。为了与划分结果相对应,需要对矩阵进行有效的重排。因此,在SpMV运算时需要准确地获取当前行的索引,避免最终计算结果出现错误。此外,为了体现负载平衡对SpMV计算的加速效果,GPU处理时采用一个线程块处理一个子块的方式,在每个线程块中一个线程处理矩阵的一行。若子块中的行数超出硬件支持的线程数目(1 024),则在预处理阶段对该子块进行分解处理。DRM存储格式的并行SpMV算法如算法2所示。在算法2的第1～2行,使用bid和tid分别记录线程块的块号和线程号,便于索引子块。第4～5行使用nrows和drm_blo数组创建变量rnum和rinx,计算子块中的行段索引。第6行使用drm_index数组来计算行索引,以确保乘积结果相加的正确性。第7～14行是本文算法的核心,利用上述索引以及drm_dnum、drm_off和drm_val数组,采用一个线程计算一行的方式,对矩阵每一行的数据进行乘积运算和累加操作,得到最终的SpMV结果,并将结果传入result数组。

算法2 DRM存储格式的并行SpMV算法输入:drm_dnum,drm_index,drm_blo,drm_off,drm_val,x,nrows。输出:结果向量result。1:int bid=blockIdx.x;2:int tid=threadIdx.x;3:double res=0;4:int rnum=tid /nrows;5:int rinx=rnum + drm_blo [bid];6:int row=tid +(drm_index [rinx]- rnum)*nrows;7:if rnum < (drm_blo [bid +1] - drm_blo [bid]) then8: for i =drm_dnum [rinx]→drm_dnum [rinx +1] do9: int val_index = (tid -rnum*nrows) +i*nrows;10: int x_index=row+drm_off [i];11: res+= drm_val [val_index] *x[x_index];12: end for13: result[row]=res;14:end if

算法2利用5个矩阵压缩数组对每个非零元进行精准索引,实现了DRM存储格式的并行SpMV内核。由于在4.1节和4.2节对矩阵进行了划分,并对划分后的行段进行了归并,使并行SpMV过程中每个线程块间的计算量达到了平衡,有效减少了线程的空闲等待,提升了整个运算过程的效率和性能。

5 实验评估

本文在第4节提出了一种新的存储格式DRM,并实现了基于此格式的并行SpMV算法。本节利用零填充数量、操作数个数方差、时间和GFLOPS等性能指标,通过与当前主流的DIA、HDC、HDIA和DIA-Adaptive存储格式进行对比实验,验证所提并行SpMV算法的有效性。

5.1 实验环境

本文实验采用的GPU型号为NVIDIA®Tesla®V100-PCIE 32 GB,包含5 120个CUDA核心SP(Stream Processor);内存容量为32 GB,含有80个流多处理器SM(Stream Multiprocessor);每个线程块的最大线程数是1 024;CPU为Intel®Xeon®Gold 6240R,主频为2.4 GHz,24核;服务器系统为Ubuntu 16.04.7,CUDA版本是11.4。

本文实验采用的稀疏矩阵为方阵,全部来自佛罗里达大学公开矩阵数据集(SuiteSparse Collection)[25]。表1描述了这些稀疏矩阵的相关信息。主要包括矩阵名、矩阵缩略图、维数和非零元个数。所选择的稀疏矩阵代表了不同类型的实际应用,包括电路仿真问题、计算流体力学问题、结构问题和电磁学问题等。

在实验中,将HDIA和DIA-Adaptive中BRCSD-Ⅱ格式的分块阈值设为32,将BRCSD-Ⅰ格式分块后的再分块阈值设为64。

5.2 零填充和负载平衡

本节从零填充和负载平衡2方面对DRM格式进行分析评估。首先验证该格式在减少稀疏对角矩阵零填充量方面的有效性。由于实验中HDIA和DRM格式的分块阈值相同,所以具有相同的零填充数量。因此,本节只对DIA、HDC、DIA-Adaptive和DRM格式进行了对比。如图10所示,在所有测试矩阵中,HDC格式取得了最少的零元素填充量,DRM格式的零填充数量小于DIA和DIA-Adaptive格式的。

对于稀疏对角矩阵来说,将非零元素按照对角线进行存储有利于维持并行SpMV过程中的访存连续性。而HDC格式对矩阵进行存储时,仅将少量对角线按照DIA的形式进行存储,剩余非零元素全部按照CSR的形式进行存储,这样虽然在零填充方面表现较好,但会引起SpMV过程中不连续的内存访问,导致降低整个运算过程的性能。

除HDC格式外,其余格式均按照对角线的形式对稀疏矩阵进行存储。其中,相比于DIA格式,DRM零元素填充数量减少地最为显著,在矩阵add32、lns_3937、ex11、rw5151和shyy161中,DIA格式填充零元素的个数分别为DRM格式的112.80,87.70,107.30,112.60和292.80倍。其中,add32和ex11填充零元素的个数是矩阵中非零元总数的940.30和82.70倍,而在DRM格式下只有8.30和0.07倍。通过观察矩阵的结构发现,其原因在于这些矩阵中存在大量的散点、长断行和长偏移,从而导致DIA格式存储的对角线条数急剧增加,从而提高了零元素的填充比例。以矩阵add32为例,采用DIA格式存储的对角线有3 767条。

Table 1 Information of sparse matrix dataset表1 稀疏矩阵数据集相关信息

Figure 10 Number of zero padding for different storage formats图10 不同存储格式的零填充数量

相比于DIA-Adaptive格式,DRM虽然不如相比DIA格式那么显著,但每个测试矩阵的零填充数量都有所减少。在矩阵lns_3937、rw5151、shipsec5和add32中,DIA-Adaptive格式的零元素填充数量分别是DRM格式的3.42,3.05,2.62和2.63倍。由此可知,DRM存储格式经过一次固定阈值的矩阵划分后,能够有效减少稀疏对角矩阵存储时的零填充数量。

然后,验证该格式在解决稀疏对角矩阵负载不平衡方面的有效性。为了更直观地展现并行SpMV计算时矩阵的负载是否平衡,将子块间操作数个数的方差作为评估负载平衡的标准。如式(13)所示,方差越小,说明子块间操作数个数的差异性越小,GPU线程块间的计算量越平衡。

本文将DRM格式与HDIA、DIA-Adaptive格式进行对比,统计矩阵分块后每块操作数个数的方差,作为最终的实验结果。如图11所示,DRM存储格式在所有测试矩阵中的子块间操作数个数的方差均小于DIA-Adaptive格式的。在除nemeth22外的其余测试矩阵中,DRM的子块间操作数个数方差均小于HDIA格式的。最小方差出现在矩阵dw2048中,因为该矩阵维数较小且对角结构明显,非零元分布比较规律,有利于DRM格式的行段归并。最大方差出现在矩阵ex11中,在该矩阵中,非零元分布不规则使矩阵对角线数量骤增,DRM行段归并后的结果欠佳,导致子块间操作数个数有一定的差异,但仍优于HDIA和DIA-Adaptive格式的。

Figure 11 Comparison of operand variance between sub-blocks图11 子块间操作数个数的方差对比

在矩阵nemeth22中,非零元素沿着主对角线周围密集排列,HDIA格式对其分块时,每块操作数个数已经达到了一定的平衡,因此DRM格式对行段进行迭代归并后,子块间操作数个数的方差略大于HDIA格式的。此外,矩阵Kuu、shyy161、Goodwin_095和Goodwin_127中包含很多散点和长断行,在采用DIA-Adaptive格式存储时,被自适应地改为BRCSD-Ⅱ格式进行存储。因为BRCSD-Ⅱ和HDIA具有相同的分块阈值,所以在这4个矩阵中,DIA-Adaptive和HDIA格式的每块操作数个数方差相同,但都大于DRM格式的。

图12显示了HDIA和DIA-Adaptive的方差与DRM方差的比值。从图12中可以看出,DRM格式相比与另外2种格式,在负载平衡方面有很大的改进。DIA-Adaptive格式的方差是DRM格式的平均66.70倍(最高197.20倍),HDIA的方差是DRM格式的平均8.20倍(最高24.80倍)。这表明,DRM格式利用矩阵重构策略,对划分的行段进行迭代归并,极大地减少了子块间操作数个数的方差,实现了GPU线程块间计算量的最大平衡。

Figure 12 Variance ratios of HDIA and DIA-Adaptive to DRM图12 HDIA和DIA-Adaptive与DRM方差的比值

5.3 SpMV执行时间和GFLOPS

基于本文提出的DRM格式,本节采用时间和GFLOPS作为性能指标,评价DRM格式的性能。在此过程中,分别采用单精度和双精度进行比较。

首先对时间性能进行对比,为了方便比较不同存储格式的性能差异,避免初始化、数据拷贝和逻辑判断等过程中由于矩阵大小或数据传输速率不同而造成的误差,本节对比的时间为SpMV内核执行时间,不包括数据传输时间。同时,为了消除偶然性误差导致的时间不准确等问题,统计结果为矩阵执行10 000次SpMV的时间,且每次测试都迭代50次,取平均值作为最终实验结果。

在双精度下对不同存储格式的SpMV执行时间进行对比,结果如图13所示。其中,DIA和HDC格式不进行分块,HDIA和DRM格式利用固定阈值进行分块,DIA-Adaptive根据矩阵非零元分布随机分块。从图13中可以看出,在所有测试矩阵中,DRM格式均优于DIA和DIA-Adaptive格式。在除shipsec5外的其余测试矩阵中,DRM格式优于HDC格式。其原因在于,矩阵shipsec5主对角线中全为非零元素,主对角线周围存在大量散点,在采用HDC存储时,DIA只存储主对角线,CSR存储剩余非零元,整体零元素填充个数为0,减少了计算资源的浪费,缩短了SpMV执行时间。因此,DRM格式略慢于HDC格式。在除nemeth22外的其余测试矩阵中,DRM格式优于HDIA格式。其原因在于,矩阵nemeth22中非零元密集分布在主对角线周围,使用HDIA格式分块存储时,子块间操作数负载更加平衡(如图11所示),因此其SpMV执行时间优于DRM格式的。

Figure 13 Execution time comparison of different storage formats under double precision图13 双精度下不同存储格式的执行时间对比

表2统计了DRM格式在双精度下的SpMV执行时间相比于其他格式的最小、最大和平均加速比。可以看出,DRM格式与DIA格式相比有很大的性能提升,获得了最高155.40倍、平均20.76倍的加速。最高加速比发生在矩阵add32中,这是因为在该矩阵中非零元素没有按照对角线形式排列,矩阵存在大量散点,DIA格式填充零元素的数量急剧增加(如图10所示),导致性能降低。此外,和HDC、HDIA和DIA-Adaptive格式相比,DRM格式也取得了不错的性能提升,分别获得了平均1.94,1.13和2.26倍,最高3.01,1.47和4.07倍的加速。

Table 2 Speedups of SpMV execution time under double precision表2 双精度下SpMV执行时间加速比

除了和以上格式对比外,本文还在双精度下将DRM与CSR格式进行了对比。实验结果表明,DRM在20个稀疏矩阵中的执行时间都小于CSR格式的,取得了平均2.46倍,最高4.82倍的加速。因此,针对更加一般的稀疏对角矩阵,DRM相比于非基于DIA构造的格式(如CSR等),仍能取得较好的性能加速。

图14展示了单精度下不同存储格式的SpMV执行时间。可以看出,相比于双精度,单精度下所有格式在20个稀疏矩阵上的SpMV执行时间均有所下降。在除shipsec5外的所有测试矩阵中,DRM格式相比于DIA、HDC、HDIA和DIA- Adaptive格式,同样获得了显著的性能增益,执行时间最短。在矩阵shipsec5中,DRM的执行时间虽然慢于HDIA和HDC格式的,但也取得了与之相近的性能。

Figure 14 Execution time comparison of different storage formats under single precision图14 单精度下不同存储格式的执行时间对比

表3统计了DRM格式在单精度下的SpMV执行时间相比于其他格式的最小、最大和平均加速比。可以看出,相比于双精度,DRM格式相对DIA、HDC和DIA-Adaptive格式的加速都有所提升,分别取得了平均23.94,2.30和2.36倍,最高188.76,6.54和5.86倍的加速。对HDIA格式的加速比减少了0.01,但仍取得了平均1.12倍(最高1.53倍)的加速。

Table 3 Speedups of SpMV execution time under single precision表3 单精度下SpMV执行时间加速比

然后对浮点运算性能进行对比,采用GFLOPS(即每秒10亿次的浮点运算数)作为评价指标,其计算如式(18)所示:

(18)

其中,OPE为矩阵中的操作数总数,N为矩阵的维数,T为SpMV的内核执行时间。

对双精度下不同存储格式的GFLOPS进行对比,结果如图15所示。从图15中可以看出,浮点计算性能随着矩阵规模的增大而增加(DRM格式的最小GFLOPS为8.2,出现在规模最小的矩阵dw2048中;最大GFLOPS为228.07,出现在规模最大的矩阵Goodwin_127中),这是因为在矩阵规模较小时,GPU中有一部分SM没有满载运行,而随着矩阵规模的增大,SM的利用率越来越高,在数据上体现为计算性能越来越高。在所有测试矩阵中,DRM格式的GFLOPS优于HDC和DIA-Adaptive格式的。在除nemeth22外的其余测试矩阵中,DRM格式的GFLOPS优于HDIA格式的;在除lns_3937、ex11、dw2048、rw5151和shy161外的其余测试矩阵中,DRM格式的GFLOPS优于DIA格式的。其原因在于,矩阵nemeth22中,HDIA格式的负载更加均衡,SpMV执行时间更短(如图13所示),因此其GFLOPS略高于DRM格式的。矩阵lns_3937、ex11、dw2048、rw5151和shy161中,尽管DRM的SpMV执行时间优于DIA格式的,但DIA格式的零填充量分别是DRM格式的87.70,107.30,5.50,112.60和292.80倍(如图11所示),在SpMV运算时,零填充量也属于操作数,需要进行乘法和加法操作,因此DIA取得了较高的GFLOPS。

Figure 15 GFLOPS comparison of different storage formats under double precision图15 双精度下不同存储格式的GFLOPS对比

Figure 16 GFLOPS speedups of different formats under double precision图16 双精度下不同格式的GFLOPS加速比

为了更直观地展示DRM格式的性能提升,本文统计了双精度下DRM的GFLOPS相比于其他格式的加速比,如图16所示。可以看出,在4种格式中,相比于HDC格式,DRM获得了最好的性能加速,提供了平均5.28倍,最大11.68倍的加速;相比于DIA、HDIA、DIA-Adaptive格式,DRM也取得了较好的性能加速,分别提供了平均1.54,1.13和1.94倍,最高3.57,1.47和2.93倍的加速。

对单精度下不同存储格式的GFLOPS进行对比,结果如图17所示。可以看出,相比于双精度,单精度的整体浮点计算性能都有所提高。同时,和双精度类似,DRM格式在大部分测试矩阵中的GFLOPS优于其余4种格式的,最高GFLOPS达到了386.604(在矩阵Goodwin_095中),相比之下,DIA格式的最高性能GFLOPS不超过300,DIA-Adaptive格式的最高性能GFLOPS不超过240,而HDC格式的最高性能GFLOPS只有120左右。总体来说,与其他方法相比,本文的方法具有更好的浮点计算能力。

Figure 17 GFLOPS comparison of different storage formats under single precision图17 单精度下不同存储格式的GFLOPS对比

图18展示了单精度下DRM格式的GFLOPS与其他格式的加速比。从图18中可以看出,与双精度相比,DRM对DIA、HDC和DIA-Adaptive的加速比都有所提升,分别取得了平均1.83,5.80和2.00倍,最高4.15,13.27和3.80倍的加速。HDIA格式的加速比略有下降,其主要原因在于,HDIA格式在矩阵shipsec5和Goodwin_127上的GFLOPS在单双精度下差异较大,单精度相比双精度,分别提升了75.9%和77.6%,而DRM格式只提升了65.7%和62.5%,因此,DRM对HDIA的GFLOPS加速比略有降低,但仍然取得了平均1.12倍,最高1.53倍的加速。

Figure 18 GFLOPS speedups of different formats under single precision图18 单精度下不同格式的GFLOPS加速比

5.4 预处理时间分析

Figure 19 Preprocessing time for the 14 test matrices图19 14个测试矩阵的预处理时间

本节对所提算法的预处理时间进行分析。预处理阶段包括矩阵划分和矩阵重构2个部分,其中,时间成本主要来自矩阵重构部分。如算法1所示,重构过程中会出现多次数据重排和归并操作,相比于矩阵划分部分,会带来较大的时间开销。本文分别计算14个测试矩阵的预处理时间,如图19所示。从图19中可以看出,所有测试矩阵的预处理时间开销平均为8.41 ms,最大为38.32 ms(Kuu),最小为0.045 ms(dw2048)。其中,对于维数9 509,包含684 169个非零元的矩阵nemeth22,只需花费0.37 ms就能完成矩阵的预处理过程。由此可以看出,所有测试矩阵的预处理时间开销都能控制在毫秒范围内。

在有限元算法中,SpMV操作是求解线性系统的主要时间开销[26]。而在求解过程中,通常需要多次迭代才能将结果收敛。如在解决大型稀疏线性系统的迭代方法(如共轭梯度和广义最小残差方法)中,求解器反复调用SpMV,通常需要数百到数千次迭代才能收敛[27]。在使用SPAI预条件的迭代求解器中,SpMV操作是最耗时的部分[28,29]。因此,在实际科学计算应用中,这种预处理成本是可以接受的。

6 结束语

针对现有存储格式对稀疏对角矩阵进行存储时出现的零填充和负载不平衡问题,本文提出了一种新的存储格式DRM,并实现了基于此格式的并行SpMV算法。DRM利用基于固定阈值的矩阵划分策略和基于迭代归并的矩阵重构策略,将输入矩阵划分为大小相等的行段,并按照行段中的操作数个数进行重新排序,将满足归并要求的行段归并为子块,实现了子块间操作数个数的最大相近。在NVIDIA®Tesla®V100平台上的实验结果表明,在几乎所有的测试矩阵中,DRM有效减少了零元素的填充量,实现了子块间操作数个数方差的最小化。与当前主流的DIA、HDC、HDIA和DIA-Adaptive格式相比,DRM格式在SpMV执行时间上分别取得了20.76,1.94,1.10和2.26倍的加速,在浮点计算性能方面,分别取得了1.54,5.28,1.13和1.90倍的加速。但是,本文研究目前只适用于稀疏对角矩阵,针对部分非零元分布不规则的矩阵,仍存在零元素填充过多的现象。未来,将对DRM的划分策略和非零元存储方式进行研究,以进一步减少零元素的填充量,提升处理不同类型稀疏矩阵的能力,并将其应用于相关领域的实际问题中。