基于双调和插值的锥束CT金属伪影校正算法*

王中昊,夏 竟,李世杰,蔡志平

(国防科技大学计算机学院,湖南 长沙 410073)

1 引言

随着计算机断层扫描CT(Computed Tomography)技术的不断发展,锥形束断层扫描CBCT (Cone Beam CT) 由于辐射剂量低、各项同性空间分辨率高等优点[1],在临床医疗、工业检测等领域的应用越来越广泛。在不含金属物体的情况下,CT装置能够拍摄出高质量图像,但如果有金属假体等植入物出现在拍摄范围FOV(Field Of View)内,将产生严重的金属伪影,大幅降低图像的质量和临床诊断价值。如何去除金属伪影对图像进行恢复,在CT研究中有着重要的现实意义。

目前,有许多针对扇形束CT的去金属伪影算法MAR(Metal Artifact Reduction)。锥束CT的相关去金属伪影算法大部分都在此基础上提出的,原理上较为相似[2],即在原始图像中将金属区域分割后,采用一定方式对金属区域进行修复,然后重建得到无金属伪影重建图像,再将原始图像中的金属部分置入,得到伪影校正图像。这一过程中,最为关键的步骤是将金属区域进行准确分割和对金属区域进行修复。应用较为广泛的算法是根据金属与其他物质的体素值的不同,设定阈值进行分割,然后使用线性插值等插值算法对金属区域进行补全。虽然这些算法能够在一定程度上抑制金属伪影,但在实际应用中效果仍不够理想,甚至会引入新的次级伪影,影响图像质量。

本文提出一种有效实用的算法,最大限度削减金属伪影。该算法通过设计有效的金属分割和补全方法,还原图像真实结构,提升图像质量,同时减少二次伪影的引入。

本文的主要工作总结如下:

(1)提出了一种基于体素均值方差比VMR(Variance Mean Ratio)的金属分割算法,通过体素点对应投影值的变化特性对体素进行区分,从而实现对金属体素的精准分割。

(2)在归一化金属伪影校正法NMAR(Normalized Metal Artifact Reduction)的基础上,提出了一种基于双调和方程插值修复的金属伪影校正算法BIH-MAR(BIHarmonic Metal Artifact Reduction),能够平滑地补全待修补区域,减少了次级伪影的引入,减小了对原始图像细节的破坏,实现了对金属伪影的消减和修复。

(3)在真实拍摄的CBCT图像上进行了实验,并与常见的去金属伪影算法进行了对比,结果表明,本文提出的去金属伪影算法效果优于其他常用的算法,能够较好地抑制金属伪影,提升图像质量。

2 相关工作

在CBCT成像过程中,投影物体中如果包含金属,则投影图像在三维重建后,金属区域周围通常会产生严重的条纹状痕迹,即金属伪影。目前主流的去金属伪影算法MAR主要分为4类[3]:投影插值法、迭代重建法、插值迭代混合法和深度学习校正法。

投影插值法算法因其直观简单、计算量小而被广泛应用,其基本原理是对投影数据中的金属部分,通过插值等方式进行替换,重建后得到无金属重建图像,再与原始重建图像中金属部分相结合得到去伪影图像。Lewitt等人[4]在1978年首先提出了投影插值法,采用多项式插值方法补全空心投影,同时对截断投影进行平滑连续性修复。Kalender等人[5]提出了针对金属伪影的线性插值校正算法LIB-MAR(Linear Interpolation Based Metal Artifact Reduction)。该算法通过搜索算法在原始数据中分割出金属迹线,再采用线性插值方法对金属迹线区域进行插值修补,最后用反投影算法对修补后的正弦图进行重建。这种算法能够较好地去除金属伪影,是后续许多改进算法的基础算法,但该算法不可避免地会引入部分新的伪影,去伪影效果有限。Meyer等人[6]提出了一种归一化去金属伪影校正法NMAR,该算法基于先验图像信息对原始数据进行归一化,从而使插值区域与周边区域更加平滑,减少了次生伪影的出现。Liu等人[7]在NMAR的基础上,针对CBCT设计出NMAR3,实现了较好的去伪影效果。Meilinger等人[8]在重建空间中对金属及部分伪影进行修正,然后对其进行正向投影,再将正向投影与原始数据进行融合得到去伪影图像。这种算法更好地保留了原始投影中的细节,但由于正向投影图像与原始图像存在一定截断现象,融合过程中同样会产生新的伪影。

迭代重建法首先对给定的一幅初始图像进行前向投影,然后将该投影与原始投影数据进行比较,将其差值作为需要校正的误差,不断对图像进行校正。通过不断迭代计算,对图像信息不断进行检验和修正直至误差达到要求范围。Gordon等人[9]首次将代数重建法ART(Algebraic Reconstruction Technique)引入图像重建领域,其根据投影数据建立方程组,然后不断迭代修正该方程组,从而得到重建区域的衰减系数。Levakhina等人[10]提出了一种基于加权迭代的校正算法,采用不同权重对投影数据进行控制,并根据投影之间的差异度设置加权因子,使用加权因子控制反投影数值。当射线穿过金属时,其本身差异度较高,加权因子设置较低,在迭代中贡献也较低,从而抑制了金属伪影的产生。这些迭代重建算法能够较好地完成对金属伪影的校正,然而由于其计算步骤繁琐,所需时间较长等问题,在实际应用中的执行难度较大。

Figure 1 Flow chart of metal artifact correction in cone beam CT图1 锥束CT金属伪影校正流程图

随着计算能力的提升和深度学习技术的发展,金属伪影校正领域近年来也出现了许多基于深度学习的去伪影算法。Gjesteby等人[11]首次提出将卷积神经网络CNN(Convolutional Neural Network)和NMAR算法进行融合,从而进一步校正NMAR处理后的金属伪影部分,进一步改善了NMAR的校正效果。Ghani等人[12]提出了一种基于生成对抗网络GAN(Generative Adversarial Networks)的金属伪影校正算法,通过训练网络对金属部分的投影数据进行补全,再通过滤波反投影[13]算法进行重建。可以看到,基于深度学习的算法在特定场景下能够取得较好的效果,但由于伪影的形成根据不同的拍摄条件和金属物体的性质具有较大不确定性,导致其泛化能力不佳且训练样本不易获得,同样存在一定局限性。

本文在归一化去金属伪影校正法的基础上,结合基于方差均值比的金属阈值分割法和基于双调与方程插值的图像修复算法,实现锥形束CT的金属伪影校正。相比现在已有的算法,本文所提算法能够在满足实用性的基础上,提升金属伪影校正效果。

3 本文算法

本文提出的锥束CT金属伪影校正算法流程如图1所示。

首先,对含金属伪影的重建图像进行双边滤波,并对金属区域进行分割,获得金属图像和去金属图像。然后,对金属图像和去金属图像进行正向投影和归一化操作,获得金属投影区域和归一化投影。接下来,对归一化投影中的金属投影区域进行双调和插值修复,得到修复的无金属图像。最后,对修复的金属图像进行去归一化和FDK(Feldkamp-Davis-Kress)[14,15]算法重建,得到无金属重建图像,并与原始金属图像进行融合,获得最终的校正图像。

3.1 图像双边滤波

原始图像经过FDK重建后,仍存在一定噪声。为了更好地去除噪声同时保留图像边缘结构,采用双边滤波器BF(Bilateral Filter)[16]对图像进行滤波,以有效地去除噪声和平滑图像,并保留图像的边缘和细节特征。BF是一种基于空间域和灰度值域的滤波器。对于一个中心像素,BF考虑其周围像素的空间距离和像素值之间的相似性,用高斯权值函数进行加权平均。其中,空间高斯权值函数根据像素之间的空间距离进行计算,像素高斯权值函数则根据像素之间的差异进行计算。通过这种方式,双边滤波器可以在保留图像细节的同时去除噪声。设V′(x,y,z)为BF滤波后的体素值,其计算如式(1)所示:

(1)

其中,V(x,y,z)为原始重建图像中位置(i,j,k)处的像素值;Np是以像素点(x,y,z)为中心的邻域像素集合;w(i,j,k,x,y,z)是双边滤波器中的权重函数,用来衡量像素(i,j,k)与像素(x,y,z)之间的相似度,其通常包括一个空间权重和一个像素权重,如式(2)所示:

w(i,j,k,x,y,z)=

wspace(i,j,k,x,y,z)×wpixel(i,j,k,x,y,z)

(2)

其中,空间权重考虑了像素之间的空间距离,其定义如式(3)所示:

wspace(i,j,k,x,y,z)=

(3)

其中,σd是控制空间权重衰减速度的参数,本文根据实践结果设置为滤波器卷积核半径。像素权重考虑了像素之间的相似度,采用高斯函数来定义,如式(4)所示:

wpixel(i,j,k,x,y,z)=

(4)

其中,σr是控制像素权重衰减速度的参数,本文设置为一个较小的值。通过控制像素间的空间距离和灰度变化范围调节像素的加权值,实现对图像的滤波。

3.2 基于体素方差均值比的金属分割

在CT影像中,使用CT值衡量组织密度,使用亨氏单位HU (Hounsfield Unit)作为CT值的计量单位。在重建图像中,准确对金属区域分割是金属伪影校正算法的基础。基于阈值的金属分割算法具有计算简单、性能稳定等优点,应用较为广泛。然而,金属与其周围的非金属物体的体素变化在重建体积中是连续的,位于金属物体边缘的非金属物体受伪影影响,其CT值接近金属的CT值,难以设定一个特定的CT值将金属进行准确地分割。例如,一般的金属CT值远大于2 000 HU,当阈值设定为2 000 HU时,金属周围部分非金属体素在伪影的影响下也会超过阈值从而被分割为金属;当阈值设定为4 000 HU时,部分金属边缘又会因其体素小于阈值而未被正确分割。因此,为了更加精准地对金属进行分割,本文引入体素对应投影点的方差均值比VMR(Variance-to-Mean Ratio)作为判断依据,辅助分割。

方差均值比即变异系数,是衡量观测值变异程度的一个统计量。本文将该比率用于CBCT 重建过程中,作为某一体素受到CT伪影影响概率的度量。方差均值比定义为某一体素在所有角度下原始投影图像对应的投影点值的方差除以该体素的CT值。设给定重建图像位置i处的体素CT值为V(i),该体素的中心点被射线源投影到投影图像pθ的位置qi,θ处,其中θ∈(0,π)为旋转角度。则体素点i的方差均值比VMR(i)定义如式(5)所示:

(5)

(6)

其中,Tmetal为金属阈值,Tvmr为VMR阈值,可通过金属物占比结合直方图法确定其取值。当某一体素点的CT值大于或等于阈值Tmetal,且VMR值小于阈值Tvmr时,该体素点判定为金属并将其在二值图像中的像素值设为1,其他区域的像素值设为0,然后对金属区域进行前向投影,得到金属物体在投影平面中的区域。

3.3 生成归一化图像

直接对金属区域进行插值修补会因为待修补区域周围不平滑而引入次生伪影[17],因此本文采用归一化金属伪影校正,需要对原始重建图像进行前向投影生成先验图像。为了减少金属伪影对非金属物的影响,首先要将原始重建图像进行量化,将金属区域填充为空气的CT值,其他区域分别填充为对应物体的平均CT值。本文实验中使用陶瓷杯和金属螺钉进行实验,可将原始重建图像量化为金属、陶瓷和空气区域,并对不同物质进行填充赋值,然后将其映射为对应的二元CT值,如式(7)所示:

(7)

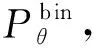
(8)

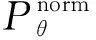
3.4 双调和方程插值补全

Δ2P(x,y)=u(x,y)

(9)

其中,Δ2表示拉普拉斯算子的平方,对归一化图像中待修补的金属区域使用双调和插值;P(x,y)表示待修补的图像区域;u(x,y)表示已知的金属区域边缘。该方程是要寻找一个能够充分平滑并且与已知边缘相符合的函数P(x,y)。

采用Canny算子从原始图像中提取出边缘信息后,将双调和方程代入求解器中,迭代求解得到待修复区域P(x,y)。双调和方程的求解公式如式(10)所示:

(10)

其中,G(x,y,s,t)是点源函数,表示在点(s,t)处放置一个单位源,产生的响应在点(x,y)处的值是该偏微分方程在特定边界条件下的响应;u(s,t)是已知的边缘信息;log(1/r)是平滑参数,r取值较小的图像就会更接近原图像,但可能会存在较多的噪声和细节,反之图像会更加平滑,但可能导致边缘信息丢失。实践证明,可以适当增大r的取值,以保证平滑度,减少次级伪影。

Figure 2 Slices of original reconstructed image图2 原始重建图像切片

(11)

最后,使用FDK算法对P′θ进行重建,得到不含金属的重建图像,将原始重建图像中的金属部分置入,得到最终的伪影消减图像,其融合过程如式(12)所示:

(12)

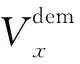
4 实验与结果分析

实验数据通过实验机器实拍获得,采用CBCT扫描方式,通过机架绕其水平轴旋转对实验物体进行正向投影。实验使用的射线源到平板探测器中心距离为600 mm,到旋转中心的距离为400 mm;射线源管电压为110 kV,电流强度为10.9 mA;平板探测器的像素矩阵尺寸为1274×1024,像素大小为0.125 mm×0.125 mm,扫描范围为0～360°,步长为0.5°,机架旋转扫描一周得到原始投影图像720幅。实验选取陶瓷杯和金属螺钉进行扫描,首先对陶瓷杯进行单独扫描作为对照数据,然后将金属螺钉附着在陶瓷杯上进行扫描得到实验数据。

采用FDK算法对采集的投影数据(图2a)进行三维图像重建(图2b和图2c)。从图2可以看出,重建图像中可见明显的呈明亮条形和暗带的金属伪影,图像质量较差。

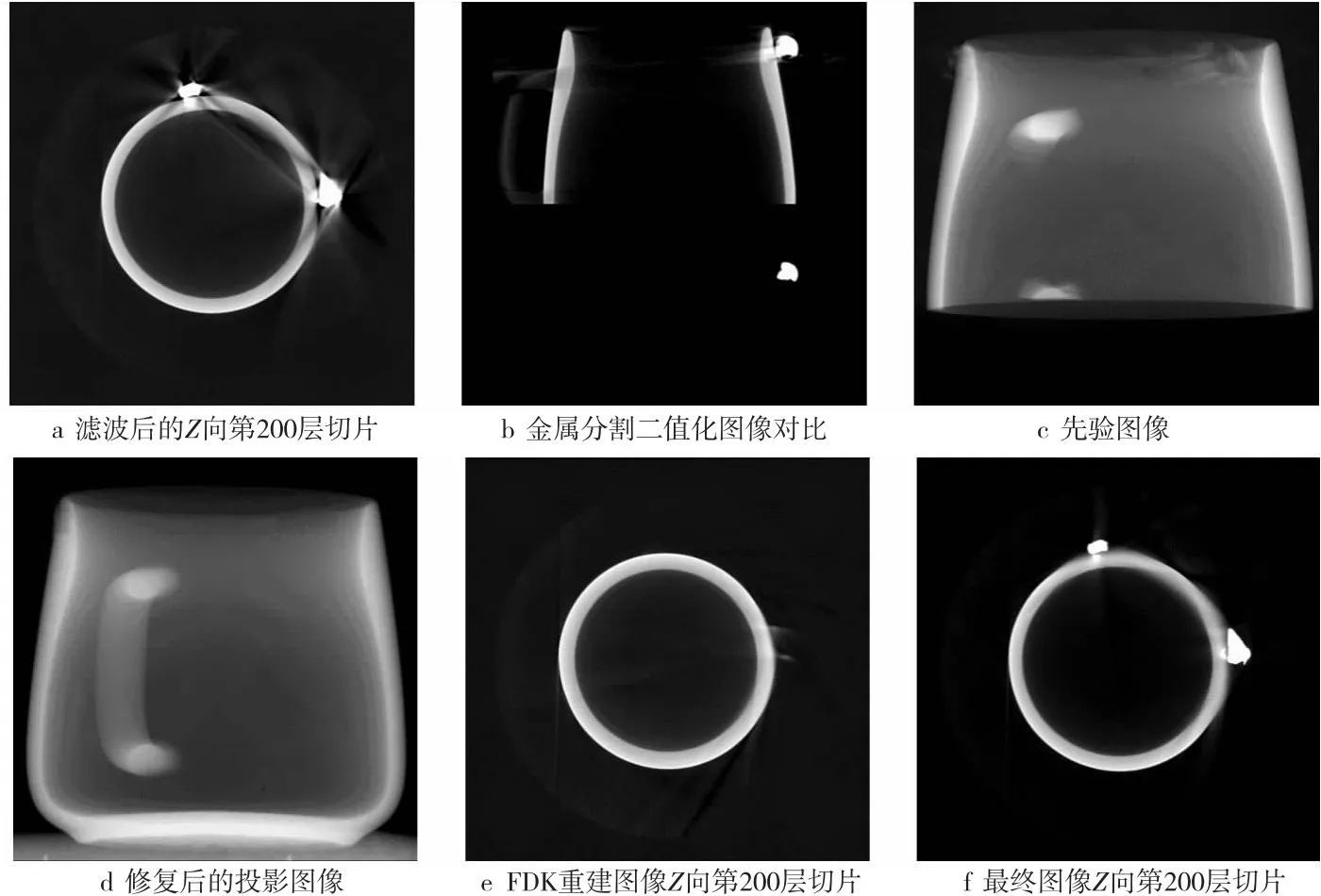
Figure 3 Images at each stage of the proposed correction algorithm图3 本文校正算法各阶段图像

采用本文提出的BIH-MAR算法进行校正。图3给出了算法的各阶段图像:(1)对重建图像进行双边滤波去除部分图像噪声,图3a显示了滤波处理后的图像;(2)结合阈值和VMR对图像金属部分进行分割,图3b为进行金属分割后得到的二值化图像对比图,上半部分为原始切片,下半部分为金属部分的二值分割,可以看到金属分割准确清晰;(3)将原始重建图像化为二值CT后进行前向投影,得到先验图像如图3c所示;(4)使用先验图像对原始投影图像进行归一化处理,对该归一化图像的金属部分采用双调和方程进行插值补全,得到修复后的投影图像如图3d所示;(5)使用修复的投影图像进行FDK重建,得到无金属伪影校正图像如图3e所示;(6)将原始重建图像的金属部分与无金属伪影校正图像进行融合,得到最终的校正图像如图3f所示。分别采用基于二次线性插值的去金属伪影算法LIB-MAR[5]和归一化去金属伪影算法NMAR[6]对原始重建图像进行校正,与本文BIH-MAR算法的结果进行对比,如图4所示。

Figure 4 Effect comparison of three metal artifact correction algorithms图4 3种金属伪影校正算法效果对比

从图4可以看出,与原始重建图像(图2c)相比,LIB-MAR算法在消减了一定金属伪影的同时,也引入了大量的次级伪影,导致部分结构被破坏,金属伪影校正效果较差;NMAR算法效果有明显提升,使金属伪影得到了较好的抑制,原始结构得到保护,图像质量有一定提升,但仍存在一些伪影未得到抑制;与这2种算法相比,BIH-MAR算法能够更大程度地对金属伪影进行消减,同时组织结构保留完整,整体图像质量提升效果明显,校正效果最优。

为了对这3种MAR算法进行定量比较[20],在伪影较为严重的Z方向第200层切片上选取3个尺寸为50×50的感兴趣区域ROI(Region of Interest)(如图5所示),以无金属投影生成的重建图像作为参考,计算ROI区域的均方根误差RMSE(Root Mean Squared Error)进行评估。RMSE的计算如式(13)所示:

(13)

Figure 5 Three ROI regions of slice of layer 200 in the Z direction图5 Z向第200层切片的3个ROI区域

表1显示了RMSE结果,在同一ROI上和所有ROI上,BIH-MAR算法对应的RMSE值相对于其他2种算法的均为最小;在所有ROI上,BIH-MAR算法对应的RMSE为0.028,比LIB-MAR和NMAR 算法的分别减少了8%和22%,表明BIH-MAR 算法对应的校正图像与原始图像的偏差最小,对金属伪影的校正效果最好,同时更好地保留了图像原始结构,与其他2种算法相比更加有效。

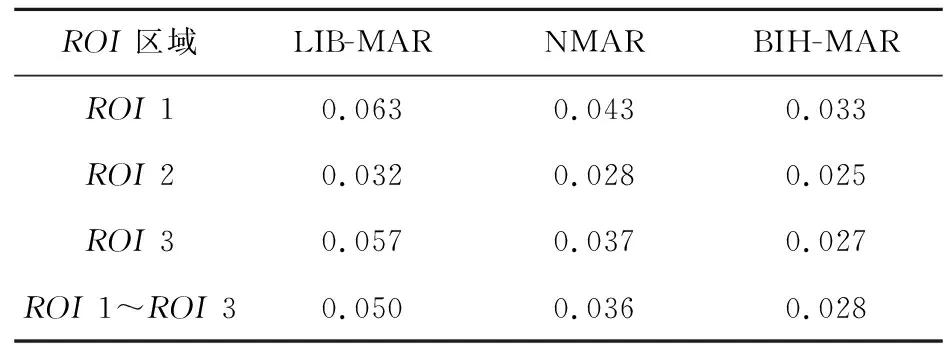
Table1 RMSE values of ROI regions of different MAR algorithms表1 不同MAR算法ROI区域的RMSE值

5 结束语

本文提出了一种归一化校正的自适应锥束CT金属伪影消减算法。该算法首先对原始重建图像进行双边滤波,去除图像底噪,然后结合VMR对金属进行阈值分割,将原始图像映射为二元CT后进行前向投影,得到不含金属的先验投影图像;然后使用先验投影图像对原始投影进行归一化,并对金属区域采用双调和方程插值补全,得到修复后的无金属投影图像;最后使用FDK算法对修复后的无金属投影图像进行三维重建,并与金属图像融合,获得最终的金属伪影校正图像。利用实拍数据对金属伪影校正算法进行有效性验证。实验结果表明,本文算法的金属伪影校正效果优于常用的LIB-MAR和NMAR算法的,从定性和定量的角度验证了本文算法的有效性。