可满足性模理论综述*
唐 傲,王晓峰,2,何 飞
(1.北方民族大学计算机科学与工程学院,宁夏 银川 750021; 2.北方民族大学图像图形智能处理国家民委重点实验室,宁夏 银川 750021)
1 引言
在计算机科学和数理逻辑中,SAT(SATisfiability)问题是指判定命题逻辑公式的可满足性问题。20世纪70年代初,SAT问题被多伦多大学的Cook[1]证明是非确定性多项式完全NPC(Non- deterministic Polynomial Complete)问题,也是首个被证明了的NPC问题[2]。SAT问题属于NP问题,且是NP难问题。许多问题如等价性检查、自动测试生成和自动定理证明等都可以在多项式时间内转化为SAT问题进行求解。SAT求解器是一种广泛应用于多个实际应用领域的核心技术,如限界模型检测[3]、软硬件形式化验证[4]、人工智能[5]和RTL(Register Transfer Level)验证[6]等。在经典领域中,SAT求解器发挥着重要的作用。命题逻辑并不是逻辑学的基础,亚里士多德的三段论逻辑[7]更接近于一阶谓词逻辑而不是命题逻辑。随着问题的研究和发展,人们已经认识到基于命题逻辑的SAT在描述能力和抽象层次上存在显著的局限性。因此,人们需要一种比SAT更好的表达方式,以获得更高的描述能力和抽象层次。当前,可满足性问题的研究已经转向了更高的抽象层次,更接近于高层次设计应用的趋势。在这种趋势下,SAT问题被扩展为可满足性模理论SMT(Satisfiability Modulo Theories)问题,基于一阶逻辑的SMT得到了广泛的关注。近年来,随着融合冲突学习机制的DPLL(Davis Putnam Logemann Loveland)算法的出现,SAT问题的研究取得了显著进展。研究人员已经提出了众多求解可满足性问题的算法,且其扩展问题也相继得到关注和研究,如最大可满足问题(Max-SAT)[8,9]、SAT计数问题(#SAT)[10,11]和SMT计数问题(#SMT)[12]。
经过扩展,SMT面向一阶逻辑进行建模,在SAT的基础上补充了量词和项,其背景理论中的原子公式不仅可以是命题,也可以是谓词。因此,SMT的描述能力更强、抽象层次更高,更接近于字级建模,具有更加广阔的应用前景。SMT支持的典型背景理论包括整数、实数、未解释函数、数组和位向量等理论。SMT求解的具体实现被称为SMT求解器(SMT solver)。SMT求解器起源于20世纪70年代末80年代初,当时一些研究人员为形式化设计了判定算法。直到20世纪90年代,研究人员对大规模问题的SMT求解器进行研究。在过去的20年,SAT求解技术的巨大进步以及命题可满足性和可满足性模理论在许多工业中的广泛应用,说明SMT近年来已经发展成为一个非常活跃的研究领域。由于SMT研究的发展和技术的进步,现在有许多强大成熟的SMT求解器,例如MathSAT5[13]、CVC5[14]、Boolector[15]、Yices2[16]、Z3[17]、SMTInterpol[18]、openSMT2[19]和SMT-RAT[20],正在快速扩展的应用程序集中使用。目前,SMT求解器应用在处理器验证[21]、等价性检查[22]、有界和无界模型检测[23]、谓词抽象[24]、RTL级设计验证[25]、自动测试用例生成[26]、类型检查[27]、规划、调度和优化等领域。
2 基本概念和定义
SMT问题是判定带有背景理论的一阶逻辑公式的可满足性问题。这些理论包括数学理论和计算机领域中的数据结构理论等。一阶逻辑是一种比命题逻辑更强大的逻辑体系,它扩展了命题逻辑,并引入了可量化的变量。一阶逻辑公式由非逻辑符号和逻辑连接符组成,其中非逻辑符号包括命题变元和常元、个体变元和常元、谓词变元和常元以及函数变元和常元。一个一阶逻辑,如果它包括一系列可量化的变元、一个或多个有意义的谓词符号,由一组包含有意义的谓词符号的公理所组成,针对特定的论域进行建模,那么它就是一个一阶理论。这些特性使得一阶逻辑非常适合用于描述复杂的逻辑问题。
2.1 命题逻辑
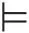
例1给定一个命题公式:
φ=p1∧(p1∨p3)∧(p2∨p3)
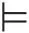
命题变元p或者命题变元的否定p称为文字L(Literal)。若干个文字的析取构成一个子句[28],记为C=L1∨L2∨L3∨…∨Ln。若干个子句的合取构成一个合取范式CNF(Conjunctive Normal Form)公式,记为F=C1∧C2∧…∧Cm。如例1给定的命题公式φ是一个CNF公式,其中子句C1:(p1),C2:(p1∨p3)和C3:(p2∨p3)。研究SAT问题是否具有可满足性,即判断是否存在一组指派能够使CNF公式为真。
2.2 一阶逻辑
定义1设一个无限集S是类型的集合,多类型签名(Many-sorted Signature)Σ是一个包含ΣS∈S类型集合、函数符号集合ΣF、谓词符号集合ΣP和变量集合ΣX的四元组,记为Σ=(ΣS,ΣF,ΣP,ΣX),满足以下条件:
(1)δ1,δ2,…,δn;δi∈ΣS,1≤i≤n。
(2)f∈ΣF是一个形式为δ1×δ2×…×δn→δ的n元函数,当n=0时,f是一个常量符号。
(3)p∈ΣP是一个形式为δ1×δ2×…×δn→δ的n元谓词,当n=0时,p是一个命题符号。
(4)在变量集合ΣX中,每个变量与S中的一个类型δi对应。
定义2项集(term)归纳定义如下:
(1)若x∈ΣX是具有类型δ的变量,且x为个体变元或个体常元,则x∈term;
(2)若f(t1,t2,…,tn)∈ΣF,n≥0,是具有类型δ的函数,f为n元函数变元或常元,其中ti(1≤i≤n,n∈N+)为项,则f(t1,t2,…,tn)∈term。当n=0时,f称为个体变元或个体常元;
(3)任意项集都能够通过有限次应用上述规则(1)和规则(2)得到。
定义3原子公式定义如下:
若p(t1,t2,…,tn)∈ΣP是n元谓词,n≥0,p为n元谓词变元或常元,其中ti(1≤i≤n,n∈N+)为项,则p(t1,t2,…,tn)称为原子公式。当n=0时,p称为命题变元或命题常元。
定义4合式公式(formula)归纳定义[29]如下:
(1)若p∈ΣP,则p∈formula;
(2)若p∈formula,则p∈formula;
(3)若φ0∈formula且φ1∈formula,则φ0⊙φ1∈formula,其中⊙∈{∧,∨,→,↔};
(4)若φ0∈formula,则∀x:δ.φ0∈formula与∃x:δ.φ0∈formula;
(5)任意formula都能够通过有限次应用规则(1)~规则(4)得到。
因此,一阶逻辑公式φ表示[29]为:
φ:=p(t1,t2,…,tn)|t1=t2|φ0|
φ0∧φ1|φ0∨φ1|(∃x:δ.φ0)|(∀x:δ.φ1)
(1)
其中,ti(1≤i≤n,n∈N+)为项,p为n元谓词变元。
定义5模型是一个二元组M=(|M|δ,Σ),|M|δ为签名Σ所有类型的非空解释域。
公式φ中一个项t的赋值为M[x]=M(x),M[f(t1,t2,…,tn)]=M(f)(M[t1],M[t2],…,M[tn])。若μ∈|M|δ,模型M将具有δ类型的变量x赋值为μ,记为M{x→μ}。
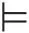
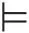
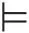
…,M(tn))∈M(p);
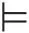
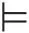
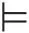
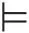
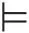
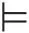
定义7理论(Theory):
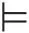
3 常见背景理论
在SMT中,人们感兴趣的模型不是任意的模型,而是在给定理论T下满足对某个签名中符号解释的模型。这些模型受到T的约束,能够保证其符号解释的一致性和可靠性。下面简单介绍一些常见的背景理论。
3.1 线性算数
线性算数LA(Linear Arithmetic)理论是只有“+”“-”的算数函数理论,按数据类型可分为线性实数运算和线性整数运算,它们都是通过任意未解释常量扩展的。其定义形式如下所示:

在线性实数LRA(Linear Real Arithmetic)理论中,x1,x2,…,xi是实数变量,在线性整数理论LIA(Linear Integer Arithmetic)中,x1,x2,…,xi是整数变量。在上面的定义中,可以使用“=”“≤”表示其他的不等式,如下所示:
(1)Σiaixi>k改写为(Σiaixi≤k);
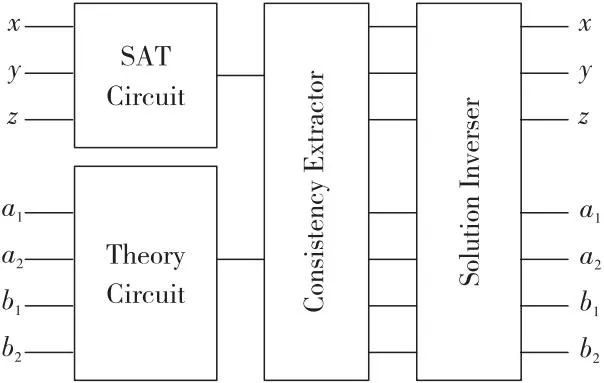
(2)Σiaixi≥k改写为Σi(-aixi)≤(-k);
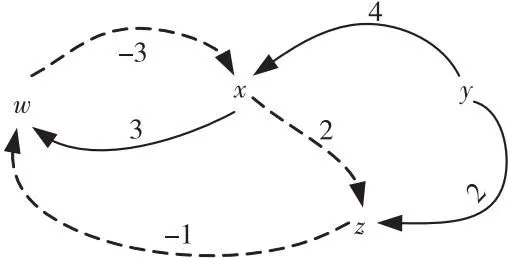
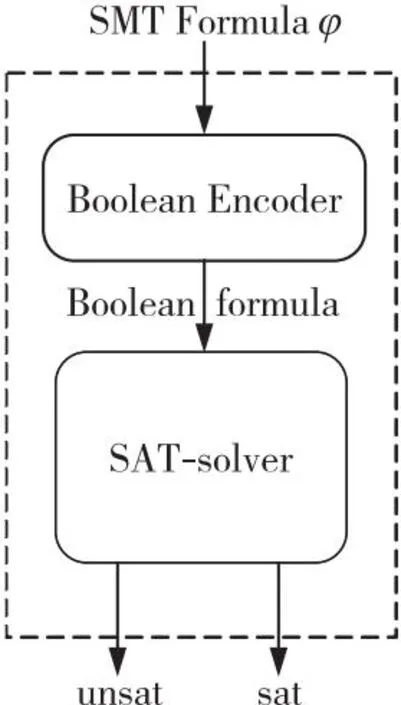
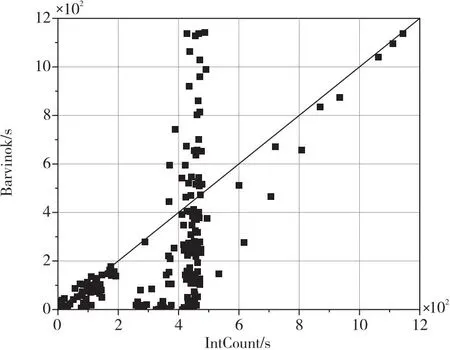
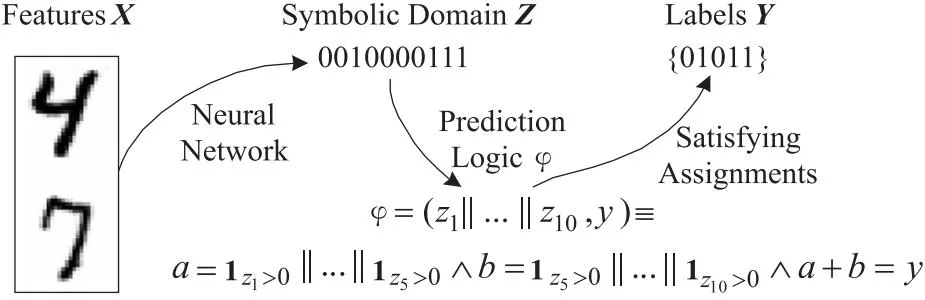
(3)Σiaixi (4)Σiaixi≠k改写为Σiaixi≤(k-1)∨(Σiaixi≤k)。 上面的(3)和(4)仅在LIA中有效。对于LRA略有变化,即将Σiaixi 需要注意的是,在算数理论中引入乘法会大大增加问题的复杂性,因此在实践中通常会避免使用。基本公式的合取范式在整数情况下会变得无法判定。虽然在实际情况下是可判定的,但其复杂度会达到双指数级别。然而,在建模和推理系统时,算数理论非常有用,尤其是在建模有限集合、程序算数、指针和内存操作等方面。因此,尽管存在一些复杂性问题,仍然需要在实践中使用算数理论去解决特定问题。如例2所示是一个典型的LA公式φ: 例2φ=(x1+2x2≤2)∧((3x3+4x4+5x5=2)∨(-x2-x3≤3)) 差分逻辑DL(Difference Logic)理论是线性算数理论的特殊情况,其定义形式如下所示: 在实数差分逻辑RDL(Real Difference Logic)中,x1,x2,…,xi是实数变量;在整数差分逻辑IDL(Integer Difference Logic)中,x1,x2,…,xi是整数变量。以差分逻辑为背景理论的一阶逻辑公式求解时,通过使用加权有向图(Weighted Directed Graph)[31],可以将一阶逻辑公式转化为图论问题,以便更直观地建模和求解。在加权有向图中,变量被表示为顶点,约束条件被表示为带有权重的有向边,带有权重的有向边刻画了约束条件的取值范围。如例3所示是一个简单的IDL示例: 例3给定一个公式φ: φ=(x-y≤4)∧(x-z>-3)∧(w-x=3)∧(z-y≤2)∧(w-z≤-1) 将公式φ重新改写为φ′: φ′=(x-y≤4)∧(z-x≤2)∧(w-x≤3)∧(x-w≤-3)∧(z-y≤2)∧(w-z≤-1) 形成的加权有向图如图1所示。加权有向图可以非常有效地检测差分逻辑的可满足性,负循环用虚线表示。从图1中可知,x到z到w到x的循环总权重为-2,可见公式φ是不满足的。 Figure 1 Weighted directed graph of example 3图1 例3的加权有向图 给定任何签名Σ,将包含该理论的所有可能的模型理论表示为TE,由于对签名Σ中符号的解释方式没有施加任何限制,所以TE也可以称为未解释函数理论EUF(Equality with Uninterpreted Functions)。EUF通常用作一种抽象技术,在许多理论中,决策问题可以被归约到未解释函数的决策过程。给定一个合取式,其中使用了未解释函数项之间的等式,可以使用同余闭包算法[30]来表示隐含等式的最小集合,这个表示可以用来检查可满足性。同余闭包算法采用有向无环图DAG(Directed Acyclic Graph)作为数据结构。如例4所示为一个EUF的例子[32]。 例4设公式: φ=(f(x)=f(y))∧(x≠y) 位向量BV(Bit Vectors)理论是基于位运算算法和数据结构的理论,用于处理进制位的表示和操作。除了标准的算数运算外,位向量还支持混合按位运算,比如NOT、AND、OR、XOR以及移位等。它可以用于解决密码学哈希函数反演和数据结构位向量操作等问题。 数组(Array)理论通常用于对程序中的实际数组进行建模,可以被视为对内存的抽象。对内存大小进行建模时,使用数组可以使模型大小与对内存的访问次数成正比。因此,在建模内存时,使用数组更有效地利用了空间,并获得了更好的性能。在实践中,这种优化经常产生显著的效果。例5给出了一个包含数组理论的示例。 数组理论有以下公式[33]定义:对于∀a∀i∀j∀v,有: read(write(a,i,v),i)=v i≠j→read(write(a,i,v),j)=read(a,j) read(i,a)=read(j,a)→i=j 例5给定公式φ=(b-1=c)∧(f(c-b+3)≠f(read(write(a,b,2),c+1))),通过数组理论公式简单推理得(b-1=c)∧(f(2)≠f(2)),所以公式φ不可满足。 SMT求解器经常涉及到不同理论的相关符号,需要同时处理2个或者2个以上的理论公式。在这种情况下,需要用到组合理论的求解方法。如果2个理论Ti和Tj的组合可以简单定义为Ti⊕Tj组合而成的理论,在这种理论中往往会存在一些共享符号,在某一理论下对共享符号的解释会影响在另一理论下的解释。因此,将不同理论的约束满足过程模块化地组合成单一过程,是一个重要的理论和实践问题。 1979年Nelson等人[34]提出了经典组合理论NO(Nelson-Oppen)判定算法。该算法中任意一阶理论是含有等式符号的自由理论,各个理论都有自己的判定过程,各个理论的签名两两不相交Σi∩Σj=∅,且解释域是无限的。其判定算法如算法1所示。 算法1 NO判定算法输入:多理论(T1,…,Ti)公式。输出:可满足/不可满足。步骤1 将输入的多理论(T1,…,Ti)公式纯化为简化后的多理论(F1,…,Fi)公式。步骤2 对每个理论Ti下的Fi进行可满足性判定。如果返回不满足,则跳到步骤4。如果推出有关共享符号的等式Ei,在存在共享符号的其他理论Tj(i≠j)下添加Ei,并更新其他理论Tj下的公式Fj,继续重复步骤2直到没有新的等式可以传播。步骤3 如果每个理论Ti下的公式都可满足,输出“可满足”,结束算法。步骤4 如果有任意一个理论Ti下的公式不满足,输出“不可满足”,结束算法。 纯化的目的(如例6)是把组合理论SMT公式分解为统一理论的公式。各理论下的Fi进行可满足性判定。若存在一个不可满足,则SMT公式是不可满足的。各理论中若有共享符号,则进行等式传播。等式传播是将共享符号及其等式推出新的等式并添加到此共享符号的其他理论中。 例6(x1-x2)≤f(x)纯化为(x1-x2≤a)∧(a=f(x))。 对于不相交无限理论组合方法往往具有指数级别的复杂度。准确地讲,如果Ti的约束满足问题的时间在O(fi(n))确定,其中i=1,2,则T1⊕T2组合问题的时间可以在O(2n2·(f1(n)+f2(n)))确定[35]。 除了经典的组合理论判定算法NO,还有其它算法或在其基础上改进的算法。Nelson等人[36]提出的Ackerman算法主要用于求解含有EUF理论的组合问题。Bozzano等人[37,38]提出了Delayed Theory Combination算法和Efficient Theory Combination via Boolean Search算法。前者通过优先考虑布尔分量和每个理论之间的相互作用,避免了各理论之间的等式传播过程,这种算法求解效率比NO算法的高;后者将真值分配的枚举器与决策过程集成起来,其关键思想是不仅要搜索公式中出现的原子,还要搜索理论的共享变量之间的所有等式的真值分配,这种算法简单而富有表现力。Tinelli等人[39]提出的Combining Non-Stably Infinite Theories算法通过在组合决策之间传播等式约束以及最小基数约束来解决基于NO算法扩展到不稳定理论的问题,试图将NO算法提升到不稳定无限理论的相交组合。Zarba等人[40]提出的Combining Sets with Integers算法是在NO算法上的改进,试图将NO算法提升到相交理论的组合,主要用于集合和整数理论的组合域。Barrett等人[41]提出了基于Shostak算法的泛化算法,该算法的核心思想是将不同的理论求解过程进行分解,然后将它们的结果进行合并,从而提高求解效率和准确性,但此算法的局限性是只适用于一些特定的背景理论,对于复杂的组合理论可能无法有效组合。 定义一个双射T2B(Theory to Boolean),表示为命题抽象。这个双射将Σ的每个命题符号映射到本身,将每个非命题符号Σ映射到另一个额外的命题符号,从逻辑上来讲它们是一致的。用B2T(Boolean to Theory)表示T2B的逆,称为细化。为了简化,常常用φp表示T2B(φ)。如例7所示为抽象的一个示例: 例7给定公式: φ=((2x2-x3>2)∨A1)∧((2x3-x4≥5)∨(2x1-x3≤6)∨A1) 抽象为如下命题框架: φp=T2B(φ)=(B1∨A1)∧(B2∨B3∨A1) SMT的判定方法有2种:积极(Eager)方法和惰性(Lazy)方法。Eager方法将SMT公式转换成等价的SAT公式,并使用SAT求解器求解。Lazy方法则将SAT求解器和理论求解器(T-solver)结合起来,先将公式抽象为命题公式以得到模型,再检查模型是否符合理论。表1对比分析了Eager方法、Lazy方法以及DPLL(T)方法的差异。 SMT求解器通常使用Eager方法[43]将一阶逻辑公式转换成命题逻辑形式,这样可以使用SAT求解器来判定可满足性。这种方法将每个原子公式视为一个布尔变量,并将不一致性添加到公式中。在调用SAT求解器之前,Eager方法会先找出所有的不一致性,这样可以保证转换后的公式与原始公式具有相同的可满足性。然而,Eager方法可能会产生太多的不一致性,导致一个简单的问题变得无法解决。为了避免这种情况,在特定情况下采用不同的编码策略,比如比特向量的SMT求解器通常使用Eager编码,以避免生成过多的不一致性。此外,正确转换每个理论公式也需要高效的转换过程,从而提高求解效率。 Eager方法的求解流程大致如下:假设每个原子公式都是一个布尔变量,然后查找所有变量之间的不一致性;接下来将公式转换成命题逻辑形式;最后将结果传递给SAT求解器并返回结果。Eager方法的框架[42]如图2所示。 Eager方法的优点是易于设置和使用,但缺点是可能会产生太多的不一致性。以下通过例8来说明算法流程[31]: Figure 2 Framework of Eager method图2 Eager方法的框架 例8给定公式: φ=(x=y)∧(x 首先,将每个原子公式看作一个命题变量:(x=y)→A,(x Lazy方法[45]在SAT求解过程中动态地添加不一致性,因此通常只需要更少的不一致性来找到解决方案。然而,为了确保Lazy方法正常运作,需要与T-solver建立接口,以验证找到的模型满足理论一致性,这比Eager方法更复杂。尽管如此,由于其灵活性好,Lazy方法是现有SMT求解器中更常用的方法。Lazy SMT(T)求解方法介绍了一个SMT求解器依据Lazy方法来判定一阶逻辑公式的可满足性。Lazy方法的框架如图3所示。 算法2很好地描述了基于Offline模式的Lazy SMT(T)的执行过程,Offline模式[30]也被称为按需引理方法。假定将一个签名Σ中的无量词 Table 1 Comparison of SMT solution methods表1 SMT求解方法对比 Figure 3 Framework of Lazy method图3 Lazy方法的框架 算法2 Lazy SMT(T)判定算法输入:φ(a QFF in the signature Σ of T)。输出:sat/unsat。1 Lazy SMT (T-formula φ) {2 φp=T2B(φ);3 while (true) {4 if (DPLL (φp,μp)=="unsat")5 return "unsat";6 else if (T-solver(B2T(μp))=="sat")7 return "sat";8 else9 φp:=φp∧μp;10} } Figure 4 Process of solving the SMT formula through the Lazy SMT(T) framework图4 通过Lazy SMT(T)框架求解SMT公式过程 公式QFF(Quantifier-Free Formula)φ作为算法的输入。其求解步骤为:首先,将SMT公式φ通过T2B抽象为命题公式φp,即公式φ中的项τi视为一个命题变元;然后,将得到的命题公式φp传递给SAT求解器,如果SAT求解器返回不可满足,则返回不可满足;如果SAT求解器找到一个模型μp,将模型μp通过B2T得到模型μ,通过理论求解器检查该模型是否是理论一致的;如果该模型是理论一致的,则返回可满足;如果该模型是理论不一致的,则将μp作为子句添加到φp中,将生成后的公式传回SAT求解器,并重新开始判定其可满足性。 Lazy方法的优点是提高了求解效率,可扩展性强,但缺点是不适用于所有类型的问题,需要构造特定的理论求解器。以下通过例9来说明Lazy SMT(T)算法流程,图4为其求解过程图。 例9给定公式: φLIA=(x≥1)∧(x≥1∨x≥3) SMT公式φ通过T2B抽象为命题公式,抽象后的命题公式φp=p1∧(p1∨p2)。然后将命题公式传递给SAT求解器求解并找到一个模型μp={p1→false,p2→true}。通过B2T细化检查发现理论不一致,将p1∧(p1∨p2)∧(p1∨p2)重新传递给SAT求解器进行求解,返回“不可满足”,因此SMT公式φLIA是不可满足的。 不管是Eager方法还是Lazy方法,都是通过某种策略将SMT公式转化为SAT公式进行判定。大多数现代SAT求解器都是基于DPLL算法框架,SMT也使用了该框架,因为SMT求解器依赖SAT求解器来判定可满足性。DPLL(T)是一种基于通用DPLL框架的算法,该算法结合了Eager方法和Lazy方法的优点。DPLL(T)算法能够嵌入许多高效的启发式策略,集成不同理论的T-solver。 假定将SMT公式φ和一个文字集合μ(初始化为∅)作为算法的输入,DPLL(T)内嵌的DPLL对φp和μp进行推理和更新。Online模式是比Offline模式更复杂的模式,算法3给出了基于Online模式[44]的DPLL(T)算法主要过程。 算法3 DPLL(T)判定算法输入:φ(a Qff in the signature Σ of T),μ(the set of T- literals)。输出:sat/unsat。1 DPLL (T-formula φ,T-assigment & μ) {2 if (T-preprocess(φ,μ)=="conflict")3 return "unsat";4 φp=T2B(φ);μp=T2B(μ);5 while (true) {6 T-decide-next-branch (φp,μp);7 while (true) {8 result=T-deduce (φp,μp);9 if (result=="sat") {10 μ=B2T(μp);11 return "sat";}12 else if (result=="conflict") {13 例10给定一个公式φ=(x≥1)∧(A∨(x<1))∧(A∨(x<1))和μ=∅。 通过T-preprocess(φ,μ)将文字(x≥1)重写为(x<1),则φ重写为(x<1)∧(A∨(x<1))∧(A∨(x<1))。然后,根据布尔约束传播BCP准则判定φ是冲突的,因此φ是不可满足的。 DPLL(T)方法通过理论预处理、选择分支、理论推导、理论冲突分析等操作进行改进,从而提高了求解效率[38,46]。由于其灵活的框架特性,DPLL(T)被许多SMT求解器所采用,例如Z3[17]、CVC5[14]、Yices2[16]、MathSAT5[13]和SMT-RAT[20]等。 近年来,SMT求解器的研究方向主要集中在求解器性能的提高和可扩展性的增强上。在性能提高方面,研究人员通过改进底层的数据结构、算法和优化策略,以及利用并行计算和GPU加速等技术来提高求解速度。增强可扩展性方面的研究包括设计新的数据结构和算法,以支持更多的理论和语言特性。同时,还有研究工作旨在将SMT求解器应用于更广泛的领域,如机器学习、网络安全和云计算等。 为了推动SMT研究和SMT求解器的发展,从2005年开始每年都会举办国际可满足性模理论竞赛SMT-COMP(Satisfiability Modulo Theories COMPetition)。表2是目前比较流行的7种求解器的简单对比总结。图5是以测试结果的排名以及综合评分为依据得到的历届SMT-COMP冠军[48-50]。值得注意的是,比赛从2019年起不再进行综合评分排名,而是根据各个赛道分别进行评分排名。目前主要赛道包括:单查询(Single Query)、增量查询(Incremental Query)、Unsat核心(Unsat Core)、模型验证(Model Validation)和并行轨道(Parallel Track)。图5中2019~2023年所列求解器是在各赛道中获胜次数最多的求解器。从图5可以看出,Z3从2011年到2017年一直保持领先,而最近几年CVC系列求解器也取得了较好的成绩,求解性能非常突出。下面简单介绍3个常见的SMT求解器,分别是Z3、CVC5和MathSAT5。 Z3[17]是微软研究院开发的SMT求解器,使用了类似于MathSAT5的冲突驱动的子句学习CDCL(Conflict Driven Clause Learning)算法和策略,同时支持更多的约束理论和语言。图6为Z3求解器的体系架构[17]。 Figure 5 Championships of previous SMT-COMP图5 历届SMT-COMP的冠军获得者 Table 2 Comparison of mainstream SMT solvers Figure 6 Architecture of Z3图6 Z3架构 首先,使用Simplifier简化公式。然后,使用Compiler进行处理,将其转换为内部数据结构和Congruence-Closure节点。接下来,Congruence-Closure Core接收SAT求解器对命题公式的赋值,并处理相关组合理论。由于Z3的体系架构易于扩展,因此可以根据需要添加新的逻辑和理论,或改进现有算法和数据结构。这些改进使得Z3在解决各种复杂问题时表现出色,使其成为目前非常先进的求解器之一。 Cai等人[58]突破传统的算法框架,针对特定理论提出了首个局部搜索算法。针对LIA设计了新的算子和评分函数,提出了新的启发式算法,从而开发了特定求解器LS-LIA(Local Search-Linear Integer Arithmetic)。针对线性实数理论和非线性实数理论[59],设计了新的基于区间的算子、断链机制和评分函数,从而提出了局部搜索算法LS-RA(Local Search-Real Arithmetic)。将这些局部搜索算法和圆柱代数分解法等加入到Z3求解器中,在Z3求解器的基础上开发了新的求解器Z3++,使求解性能得到增强。 合作有效性检查器CVC(Cooperating Validity Checker)系列求解器是一组重要的自动定理证明工具,被广泛应用于研究和实践中。CVC4[60]是CVC3的重构版本,旨在创建一个更加灵活和高性能的架构。CVC5是Barbosa等人[54]开发的SMT求解器,是该系列最新的求解器。它建立在CVC4的代码基础和架构之上,在性能和功能上都有很大的提升,是目前非常先进和高效的SMT求解器之一。CVC5采用了自适应的CDCL算法,并支持在广泛的背景理论及其组合中对无量词和量化公式进行推理,包括可满足性模理论库SMT-LIB(Sat- isfiability Modulo Theories LIBrary)[61]中所有标准化的理论。此外,它还原生支持一些非标准理论和理论扩展,如分离逻辑、数列理论、关系理论和具有超越函数的实数理论扩展。图7为CVC5求解器的体系架构[14]。 Figure 7 Architecture of CVC5图7 CVC5架构 CVC5提供了一个C++API作为主接口,并且在解析器上构建了文本命令界面CLI(Command-Line Interface)。其核心引擎是基于CDCL(T)框架的SMT solver模块。SMT solver模块由预处理(Preprocessor)模块、重写(Rewriter)模块、命题引擎(Propositional Engine)以及理论引擎(Theory Engine)4个核心组件组成。预处理模块的功能是在进行可满足性检查前,通过一系列转换(包括归一化、简化和还原等过程)对输入的公式进行预处理,以保持可满足性。重写模块的功能是在求解过程中将term通过重写规则转换为语义等效的规范形式。命题引擎是CDCL(T)的核心引擎,它接收输入公式的命题抽象,并在该抽象上产生满足该公式的模型。理论引擎是负责检查命题引擎,判定理论文字的一致性。除了标准的可满足性检查,CVC5还提供了额外的功能,例如归纳、插值、高阶推理、语法指导合成SyGuS(Syntax-Guided Synthesis)以及量词消除。 通过比较Z3(版本4.8.12)和CVC4(版本1.8)来评估CVC5(版本1.0.0)的整体性能。实验环境是配置为Intel®CoreTMi5-8265U CPU和8 GB RAM的电脑,在非增量SMT-LIB(2020)基准测试实例中每个求解器的运行截至时间为1 200 s。实验结果如表3,其中#inst表示实例数。 Table 3 Results of CVC5/4 and Z3 on SMT-LIB instances表3 CVC5/4和Z3在SMT-LIB实例上的结果 通过实验分析可知,3种SMT求解器都支持广泛的理论,且都是目前比较先进的求解器。总的来说,CVC5解决的实例数最多,性能好于CVC4的。因为添加了与证明相关的重构,CVC5在无量词线性算数中解决的实例数相比CVC4的要少。同时,由于位向量求解器还没有针对理论组合进行优化,CVC5在无量词等式位向量中解决的实例数比CVC4的要少。此外,在等式线性算数和无量词等式非线性算数中解决的实例数比Z3的少,从而可以针对这些特定的理论求解进行优化。 MathSAT5是由Cimatti等人[13]开发的SMT求解器,它在支持大多数SMT-LIB理论及其组合的同时,显著改进了对增量解法的支持,提供了如Unsat内核、插值和ALLSMT等在内的许多功能[52]。图8为MathSAT5求解器的体系架构[13]。 Figure 8 Architecture of MathSAT5图8 MathSAT5架构 MathSAT5由Environment和API 2部分组成,在Environment中协调求解器中的各个子组件。预处理器是一个term重写引擎,其作用和CVC5重写模块的相似。编码器的作用是将一阶逻辑公式抽象为CNF命题公式。MathSAT5的核心由SAT引擎和理论求解器组成,它们按照标准的DPLL(T)方法进行交互[30]。SAT引擎允许集成外部第三方的高效SAT求解器。理论管理器是SAT引擎和单个T-solver之间的统一接口,它们只与理论管理器进行交互。这样做的优点是T-solver的管理较容易,从而不会影响系统的其他部分。SAT引擎与理论管理器以及模型或证明器组件进行交互,其中后者负责生成可满足公式的模型,并为不可满足的公式生成反驳证明。 表4为MathSAT5和MathSAT4(版本4.2.17)在SMT-COMP(2009)基准上的测试结果[13]。从结果中可以明显得出结论,即MathSAT5的性能优于MathSAT4的性能。 随着SMT的发展和深入研究,SMT被应用于各种领域,SMT的扩展问题#SMT也相继被研究和应用。 Table 4 Experimental results of MathSAT4 and MathSAT5表4 MathSAT4和MathSAT5的实验结果 在逻辑理论中,#SMT问题是一个复杂的模型计数问题,它不仅需要找到一组解来满足一阶逻辑公式,还需要计算出满足该公式的所有解的数量。由于#SMT问题的复杂度是#P完全的,使得寻找快速且精确的求解算法变得困难。对于#SMT问题,目前大多数研究都是以LIA、LRA和BV理论为背景的SMT公式的模型计数。对于以线性算数为背景理论的#SMT问题,可以将其转化为计算一阶逻辑公式所形成的凸面体的体积。而对于以位向量理论为背景的#SMT问题,大多采用基于哈希的模型计数近似方法[62]。 Ma等人[63]在早期提出了一种精确求解小规模线性问题计数的方法,但该方法并不适用于大规模问题。周俊萍等人[12]针对线性算数理论提出了一种基于局部搜索算法求解大规模#SMT问题的近似算法。该算法基于DPLL(T)框架,通过使用群体规则减少计算体积的次数,再通过一种差分进化方法[64,65]枚举各个有解域,从而提高求解效率。Chistikov等人[66]提出了一种以LIA和LRA为背景理论的SMT公式的模型计数算法,该算法能够给出具有近似误差形式边界的近似解。Borges等人[67]总结了适用于复杂非线性约束的模型计数技术,指出最有实用性的技术是近似模型计数和位级哈希。Ge等人[68]提出了一个计算和估计线性算数理论约束解空间体积大小的工具VolCE(Volume Computation and Estimation),该工具可以计算和估算LRA公式形成的凸面体的体积,统计LIA公式位于解空间的样本点。由于VolCE使用了高效的启发式算法,对于大规模的LRA公式也可以高精度地进行体积估计。Gao等人[69]提出了用马尔科夫链蒙特卡洛抽样策略估计以LIA为约束条件的解空间体积的近似方法,该方法和其他先进方法相比具有竞争力且有较好的可扩展性。Kim等人[70]提出了一种结构近似模型计数算法用于结构位向量模型计数。该算法通过分析SMT公式结构以确定其解个数的上下界,且不依赖于决策过程。基于此算法构建了SMC(Structural Model Counter)计数器,通过对比其他先进近似模型计数器,验证了该算法是一个快速的多项式算法。 Ge等人[71]于2019年提出并证明了线性约束条件下通过空间量化近似整数计数的理论边界,通过理论分析提出了一种线性约束的近似整数解计数方法,并基于此方法提出了近似整数计数器。此方法首先应用高斯消元减少等式,然后通过线性规划计算Mi(P)和mi(P),并通过式(2)计算误差err。最后通过体积计算工具和体积估计工具输出近似值、下界和上界组成的三元组。通过实验分析可知,此方法可扩展性强且非常高效。 (2) 随后,Ge等人[72]又提出了一种新的整数计数方法,该方法利用基于列消去和行消去的分解技术,进一步提高了整数计数算法的性能。该方法首先消除选择的行和列得到新约束;接着,再从新约束中确定所有的连通分量,这些分量对应不同的变量集、子矩阵和子向量;然后,问题P可以被分为k个子问题,进而将线性约束的整数计数问题分解为独立的子问题。基于该方法提出了Intcount计数器,采用来自程序分析和简单时间规划的基准[71],与先进的整数计数器Barvinok进行对比,结果如图9所示[72]。图9中,横纵坐标均代表计数器的运行时间。可以看出,IntCount在一定时间内能处理更多的实例,可见该分解计数方法在扩展计数器能力上是非常高效的。 Figure 9 Performance comparison of IntCount and Barvinok on benchmarks图9 IntCount和Barvinok在基准上的性能比较 #SMT问题的解决在软硬件形式化验证、人工智能等多个领域有着重要的应用意义。在软件测试领域,可以使用#SMT问题生成具有特定属性的测试用例。在人工智能领域,#SMT可以用于解决资源分配、路径规划等问题。#SMT在加密和区块链领域也有广泛的应用,它可以用于验证加密算法的安全性,检测密码破解的可能性,并对加密协议和区块链智能合约提供形式化分析。为了解决#SMT问题,研究人员已经开发了许多基于启发式方法的求解器。尽管这些求解器在实践中已经取得了一定的成功,但在处理大规模问题时仍然面临着计算效率和精度的挑战。 近些年,一些技术[73]已经将求解器集成到深度神经网络DNNs(Deep Neural Networks)中。这些技术展示了归纳学习和符号推理技术之间搭建桥梁的前景。这类技术在训练过程和推理过程中均可使用。Wang等人[74]提出了一种可以集成到DNNs中的可微MAXSAT层,该层采用快速坐标下降法高效计算前向和后向通道。Vlastelica等人[75]将求解器与深度学习结合起来,以解决原始输入数据上的组合问题。 Fredrikson等人[76]提出了一套将SMT求解器集成到DNNs的前向和后向通道的方法,被称为SMTLayer。通过这种方法,可以将丰富的领域知识以数学公式的形式编码到神经网络中。SMTLayer是一套用于计算层的前向和后向传递算法,其行为由一组用户定义的SMT约束来确定。SMTLayer不包含可训练的参数,而是完全依赖于模型设计者提供的一组SMT约束φ来定义其功能。SMTLayer主要用于DNNs的顶部,从传统DNNs层的堆栈中获取输入,将原始输入特征转换为嵌入SMTLayer的约束条件φ(z0,…,zp-1,y0,…,yq-1)的项,并产生与φ和给定项一致的输出。图10是一个MNIST加法示例[73]。 Figure 10 Example of MNIST addition图10 MNIST加法示例 算法4给出了前向传递算法的基本框架。在前向传递[76]过程中,对φ的限制是z和y必须是布尔值的向量。除此之外,φ中出现的其它符号可以是来自底层SMT求解器支持的任意域。 算法4 基于SMTLayer的前向传递算法输入:前一层的输出z0,…,zp-1,公式φ(z0,…,zp-1,y0,…,yq-1)。输出:浮点值y0,…,yq-1。步骤1 在φ中替换zi的基本项,构建公式^φ。步骤2 判定^φ是否可满足。如果可满足,跳到步骤3;如果不可满足,跳到步骤4。步骤3 获取求解器模型y0,…,yq-1,通过将false映射为-1,true映射为1,输出浮点值y0,…,yq-1。步骤4 输出y值0。 算法5给出了后向传递算法的基本框架。在后向传递[76]过程中,可以找到输出损失更小的输入特征,并且通过将这些特征的梯度传回到前面的层来进行参数更新,以优化神经网络并降低损失函数值。 算法5 基于SMTLayer的后向传递算法输入:前向传递的输入和输出,二元交叉熵损失函数l(y,y*)的梯度,公式φ(z0,…,zp-1,y0,…,yq-1)。输出:梯度Gz。步骤1:使用梯度、输入和输出计算修正后的输出^y,该输出对应损失更小的输出;步骤2:使用^y判定输入中哪些分量与φ和^y不一致,通过梯度计算的方法计算梯度Gz;步骤3:向前一层输出相应的梯度Gz。 综上,SMTLayer是一个将SMT求解器集成到DNNs中的方法,使用SMTLayer可以降低对训练数据的依赖,提高训练效率,并且表现得非常健壮。 随着量子技术的迅猛发展,验证量子程序的正确性、优化量子编译过程以及诊断量子系统中的错误变得越来越具有挑战性。为了应对这些挑战,研究人员开始探索将SMT求解器与量子技术相结合的方法。 Deng等人[78]提出了量子程序的元编程框架MQCC(Meta Quantum Circuits with Constraints),通过MQCC的编译器生成合适的约束,再结合SMT求解器求解,生成优化的、可运行的程序。Seino等人[79]提出了一种基于SMT求解器的量子电路综合方法,该方法由CNOT(Control-NOT)门、H(Hadamard)门和T门组成,满足NNA(Nearest Neighbor Architecture)限制。该方法通过处理量子特定的T门和H门的功能,利用Z3求解器最大限度地减少CNOT门的数量。Murali等人[80]提出了一种Scaffold量子编程语言的编译器,其中的优化是专门针对具有数百个量子比特的噪声中尺度量子NISQ(Noisy Intermediate-Scale Quantum)机器。编译器从Scaffold程序中提取门,并构建一个同时考虑程序特性和机器约束的约束优化问题。然后,使用Z3求解器将程序量子比特映射到硬件量子比特、调度门(Gate Scheduling)和CNOT路由门(CNOT Routing),进而减少整体执行时间。 量子SMT求解器是将量子技术与SMT结合起来开发的求解器。Lin等人[81]提出了基于量子算法Grover[82]的BV理论的量子SMT求解器。其利用量子系统中叠加和纠缠的性质,使求解器能够同时考虑所有的输入,并在一次迭代中检验它们在布尔域和理论域之间的一致性。量子SMT求解器的整体框架如图11所示。整体架构由4个部分组成。 Figure 11 Overall framework of quantum SMT solver图11 量子SMT求解器整体框架 SAT Circuit的作用是确定布尔域的解。Theory Circuit的作用是确定理论是否是一致的、不冲突的。Consistency Extractor的作用是结合量子系统来识别布尔域和理论域都一致的解。Solution Inverser的作用是反推SMT公式的解。 综上,SMT求解器作为一种强大的自动推理工具,可以将量子问题转化为SMT约束来解决复杂的约束问题,也可以将SMT求解器与量子计算相结合来开发出量子SMT求解器,从而提高求解器的求解速度以及发现所有解的能力。这种结合对量子领域发展和提高SMT求解器性能均提供了新的可能性。 近年来,随着计算机硬件的不断发展和计算能力的提高,SMT领域取得了一些重要进展。然而,SMT在实际应用中仍然面临着诸多挑战。一方面,SMT需要求解更复杂的逻辑公式(例如包含量词的公式),求解效率和可扩展性是其主要的瓶颈。另一方面,SMT的求解精确性和容错能力也是关键,特别是当逻辑公式不完整、不一致或含有错误时,需要更加精确、健壮的算法和求解器来解决问题。未来,SMT可以在以下几个方面得到进一步的研究和发展: (1)随着机器学习技术的发展,可以将SMT和机器学习算法结合,以解决更加复杂和庞大的问题。 (2)随着SMT应用范围的不断扩大,提高SMT求解器的效率和速度成为了研究重点。未来的研究将致力于针对特定背景理论开发更加高效的求解器。 (3)#SMT具有较高的计算复杂性,在最坏情况下可能需要指数级时间。为降低计算复杂性,需研究更高效、通用且可扩展的算法,以适应不同类型和规模的#SMT。同时,加强#SMT的理论研究,如复杂性分析和算法正确性证明,也有助于设计更有效的解决方案。 (4)随着量子技术的发展,SMT也将面临新的挑战和机遇。未来的研究将探索SMT与量子算法相结合,扩展到其他更多理论,以加快求解效率和提高求解精度。 总之,本文从SMT出发,总结了背景理论、求解方法、求解器、扩展问题和最新应用。对于SMT的求解还有非常大的研究和发展空间。未来的研究将致力开发更加精确和高效的算法和求解器,并将其应用于更多的领域以解决实际问题。3.2 差分逻辑

3.3 相等理论
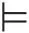
3.4 位向量
3.5 数组
3.6 组合理论

3.7 抽象
4 SMT判定方法
4.1 积极方法
4.2 惰性方法
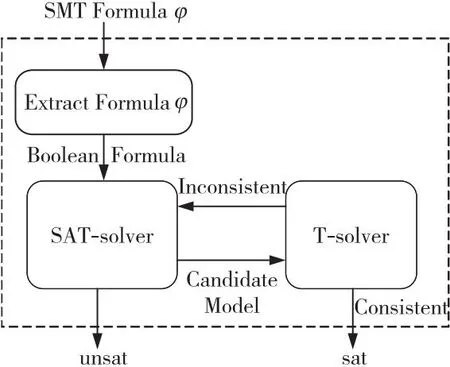

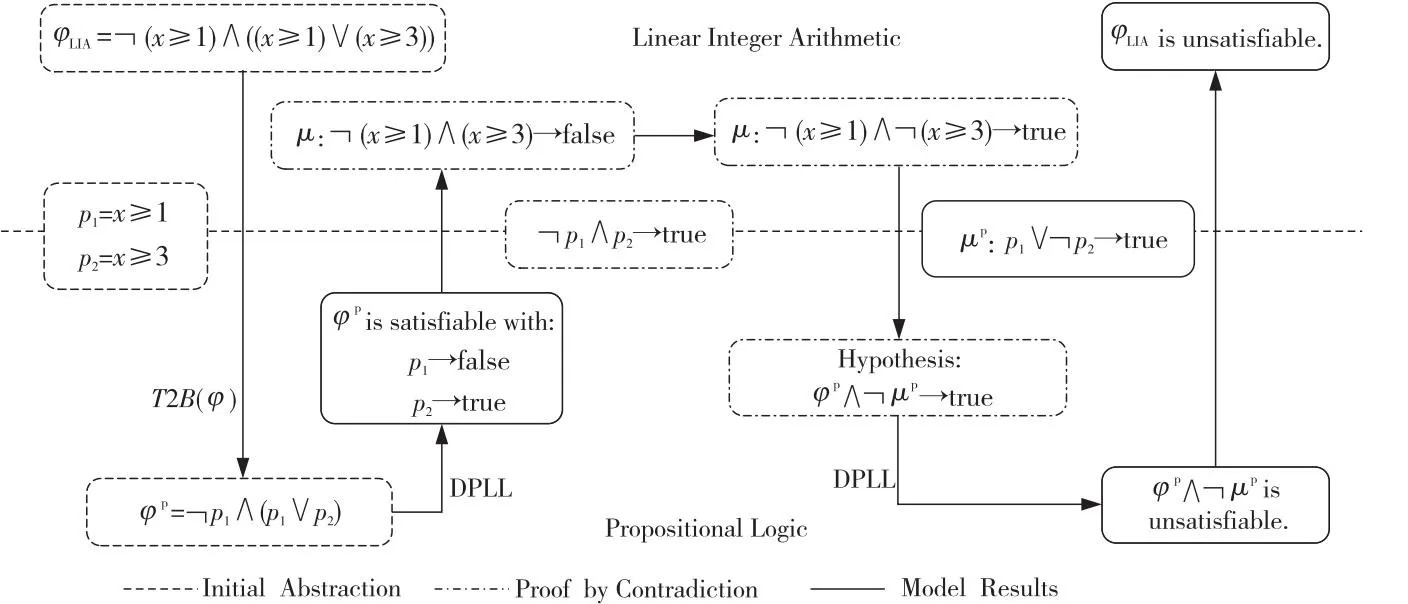
4.3 DPLL(T)
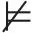

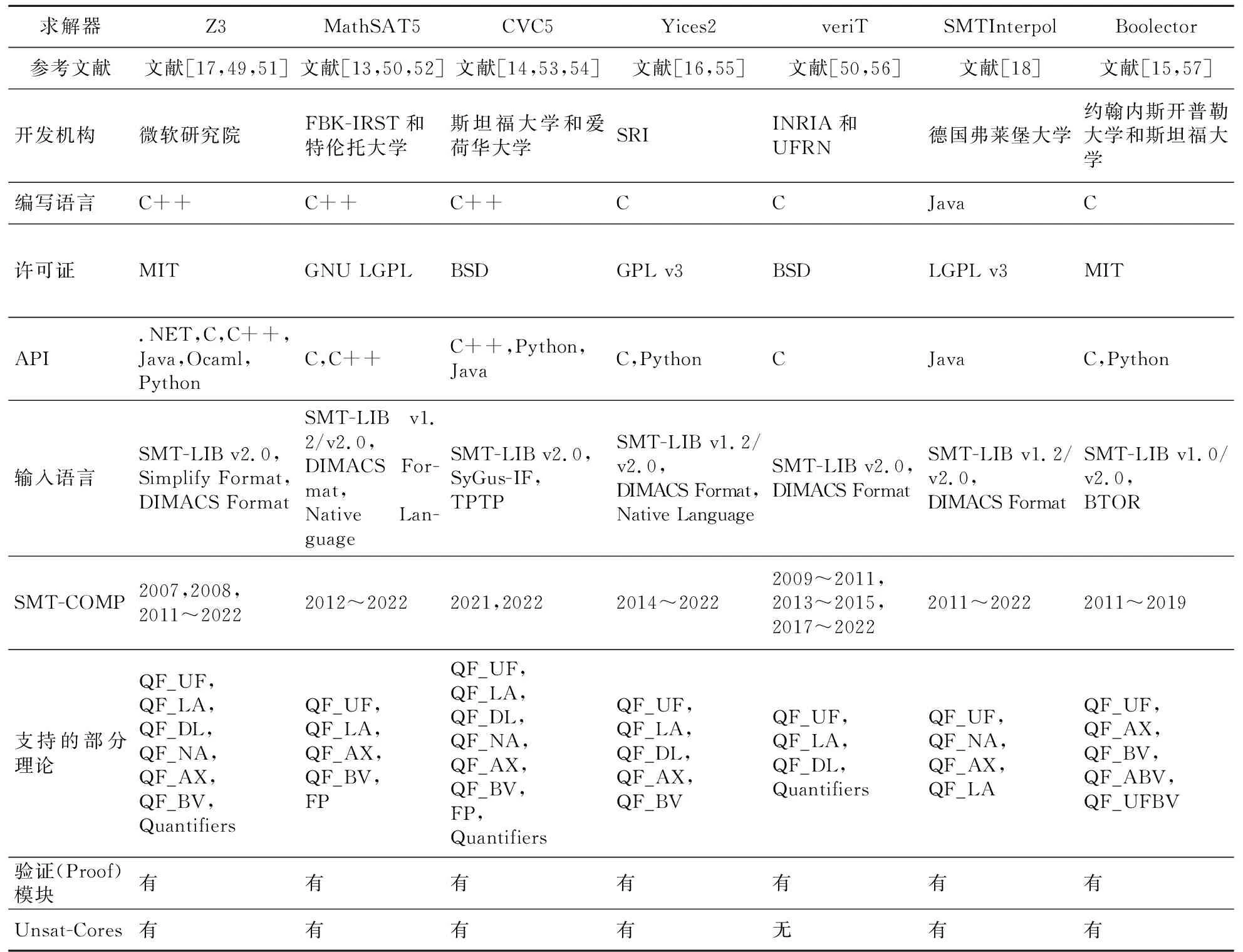
5 SMT求解器
5.1 Z3求解器

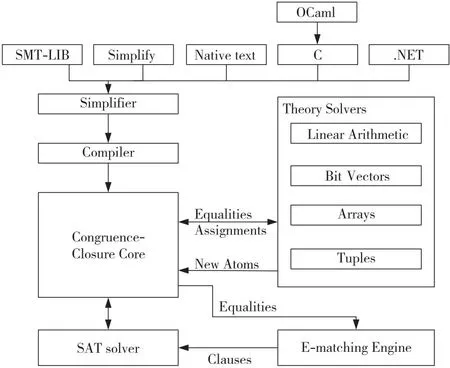
5.2 CVC5求解器
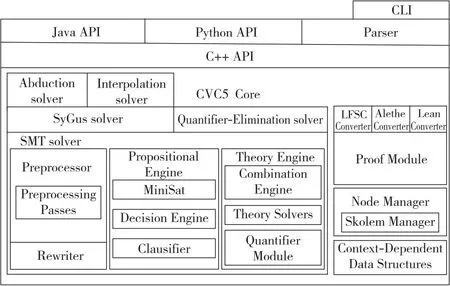

5.3 MathSAT5求解器
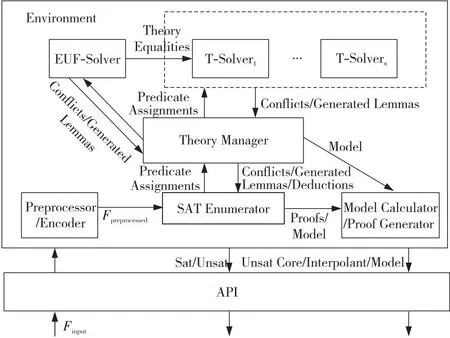
6 SMT的扩展及其应用
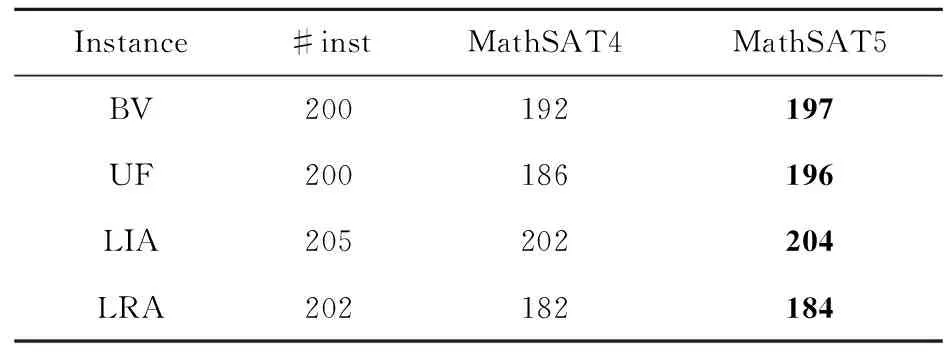
6.1 #SMT
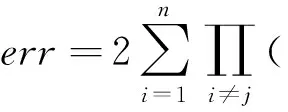
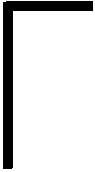
6.2 SMT在深度神经网络中的应用


6.3 SMT求解器与量子计算的结合
7 结束语

