贴敷约束阻尼层的螺栓连接板半解析动力学建模及减振分析
张荣飞,孙 伟,骆海涛,张 辉
(1.东北大学 机械工程与自动化学院,沈阳 110819;2.东北大学 航空动力装备振动及控制教育部重点实验室,沈阳 110819; 3.中国科学院 沈阳自动化研究所,沈阳 110819)
卫星、空间站等航天器的太阳翼帆板多为可展开式的铰接多板结构,在完全展开锁定的状态下为典型的挠性结构[1-2],在外部干扰或内部干扰的作用下极易产生振动。由于太空属于真空低阻尼环境,使得太阳翼帆板的振动难以得到快速的衰减,长时间的振动会造成机械结构的破坏和敏感元件的损伤,从而影响航天器的姿态控制和正常工作[3]。因此为了减小振动对航天器正常运行的影响,对太阳翼帆板的振动抑制研究势在必行。
根据太阳翼帆板的工作的原理,目前对于其振动抑制方法有抗振源隔振[4]、传递路径隔振、有效载荷隔振[5]、主动振动抑制[6]和被动振动抑制[7-8]等。抗振源隔振、传递路径隔振和有效载荷隔振对结构设计难度较大,研究通用性不强。主动振动抑制对机电控制系统的设计要求非常高,会增大控制系统的复杂性。相比较于上述振动控制方法,利用贴敷约束阻尼层(constrained layer damping,CLD)对结构实施被动振动抑制,具有结构简单、经济性好、减振效果明显等特点。其减振机理可描述为利用阻尼层产生应变而将振动的能量转化为应变能,并以热能进行耗散来达到减振的效果[9]。因而,可以考虑将约束阻尼层贴敷在太阳翼帆板的非工作面上以实现对其过大的振动进行抑制,本文就是以太阳翼帆板的约束阻尼层减振为背景,并利用双搭接的螺栓连接板对帆板进行模拟研究。需要说明的是双搭接的螺栓连接板结构在土木工程、机械工程、航空航天等领域[10-11]也有应用,因而对该结构进行减振研究具有较大的工程价值。
为了有效实施双搭接螺栓连接板约束阻尼层减振,需要研究其动力学建模方法,主要技术要点包含对约束阻尼层结构及双搭接螺栓结合部的模拟。
在贴敷约束阻尼结构建模方面,目前还没有针对双搭接螺栓连接板结构贴敷约束阻尼层减振的研究,但是面向单板、单梁、单壳的建模方法也可以作为本研究的参考。例如Xie等[12]利用有限元法研究了全覆盖约束阻尼层的悬臂层合板,对三层都考虑了剪切应变和拉伸应变,建立了动力学模型。Zheng等[13]利用半解析的方法针对贴敷约束阻尼层的悬臂梁进行了动力学建模研究,考虑了基梁与约束层之间的层间剪切,基于能量法和假设模态法推导了系统的运动方程。Song等[14]基于Donnell壳理论考虑黏弹性层的剪切变形,利用半解析法创建了全贴敷约束阻尼层的圆柱壳的动力学模型,求解了固有频率、模态振型和模态损耗因子等。Xu等[15]基于经典板理论考虑层间剪切变形,同样利用半解析法创建了贴敷矩形约束阻尼层的碳纤维悬臂薄板的动力学模型,并求解了固有频率、模态振型、振动响应和模态阻尼比等。从以上研究可以看出,有效模拟出层间剪切变形是约束阻尼结构建模的关键,这方面的建模方法已经相对成熟。另外,考虑到半解析法具有较高的求解效率,这里将采用半解析法研究贴敷约束阻尼层的双搭接螺栓连接板的动力学建模问题。
在双搭接螺栓结合部建模方面,当前的研究成果较少。例如Oskouei等[16]利用高保真的全三维有限元模型,针对双搭接螺栓连接板结构进行了力学分析,结果显示双搭接螺栓结合部呈瓦罐状压力分布。Li等[17]针对单螺栓搭接的梁结构,利用弹簧质量系统模拟出了单搭接螺栓接头的位移和载荷分布,同时将该方法扩展应用于双搭接螺栓连接接头。但是,关于单搭接螺栓结合部已有大量研究,Ye等[18]基于有限元软件,针对单搭接螺栓连接板结构,利用虚拟材料法建立了单搭接螺栓连接结合部的动力学模型,求解了固有频率、振动响应等。Liu等[19]利用半解析法在针对单搭接螺栓连接板结构,考虑螺栓结合部处的螺栓影响区域,在螺栓影响区域内用高阶多项式描述了复弹簧单元的刚度和阻尼等相关参数,并求解了固有频率、模态振型、振动响应等。Wang等[20]同样利用半解析法针对单搭接螺栓连接的多板结构,采用变刚度的人工弹簧模拟螺栓影响区域中非均匀分布接触压力,求解了系统的振动响应。从以上评述可以看出,当前关于双搭接螺栓结合部的力学建模多采用高保真的全三维有限元法,其结构自由度较大,求解效率慢,在静力学求解时能满足要求,但可能并不适用于本文的动力学建模问题。而对于单搭接螺栓结合部,采用弹簧-阻尼单元模拟结合部的力学特性是一种适用于螺栓连接结构动力学求解的重要方法。因此,本文将在考虑双搭接螺栓影响区的前提下,研究用复面弹簧单元和修正质量创建双搭接螺栓结合部力学模型的方法。
综上,本文以模拟太阳翼帆板的双搭接螺栓连接板为对象,研究对其局部贴敷约束阻尼层进行减振设计的方法。具体地,以贴敷“H型”约束阻尼层的双搭接螺栓连接板为对象,采用半解析法创建了该复合结构的动力学模型,并组建了试验系统对所创建的动力学模型的合理性进行了验证。最后,基于创建的模型分析了贴敷面积和阻尼层厚度对双搭接螺栓连接板振动特性的影响。
1 半解析建模
本部分首先描述了基于模态应变能的双搭接螺栓连接结构“H型”约束阻尼层减振方案的选取依据,其次描述了局部贴敷约束阻尼层的双搭接螺栓连接薄板的半解析建模方法,具体地进行了约束阻尼层板和双搭接螺栓结合部的建模及能量分析,之后推导了整个结构的动力学方程。需要说明的是对于其他贴敷方案,以下所研究的建模方法也完全适用。
1.1 贴敷方案的确定
这里从满足多模态减振、减少贴敷质量以及对原结构振动特性影响较小等方面来确定约束阻尼层的贴敷方案。考虑到将阻尼层贴敷到模态应变能较大的区域对减振有利,利用ANSYS有限元软件对双搭接螺栓连接薄板进行模态应变能分析,前4阶的模态应变能分布如图1所示。由图1可知,第1阶、第2阶和第3阶的模态应变能较大处,主要分布在左边的板上靠近螺栓孔附近。同时,相关研究已经表明将约束阻尼层贴敷在夹持区附近对原结构的固有频率影响较小。综上,本文选取仅在左侧板上(包含夹持区的板)贴敷“H型”约束阻尼层的方案。

(a) 第1阶模态应变能
1.2 模型描述
所研究的局部贴敷约束阻尼层的双搭接螺栓连接薄板结构示意图,如图2所示。左侧的板定义为A板,右侧的板定义为B板,在A板单侧贴敷有3块约束阻尼层片,共同构成了“H型”贴敷。A板由夹具固定,两板之间采用两个双搭接的双螺栓连接方式连接。沿A板的两条边建立笛卡尔坐标系(x-y-z),其中Lb,Wb,Hb分别表示基板的长度、宽度和厚度;a1,b1,a2,b2,a3,b3,分别表示A板上3块约束阻尼层的长度和宽度;x1,y1,x2,y2,x3,y3,分别为确定约束阻尼层位置的坐标;Lv,Wv表示“H型”约束阻尼层区域的长度和宽度(其中Lv=a1+a2+a3,Wv=b1),Hv和Hc分别表示黏弹性层和约束层的厚度;d为A板与B板的间距。
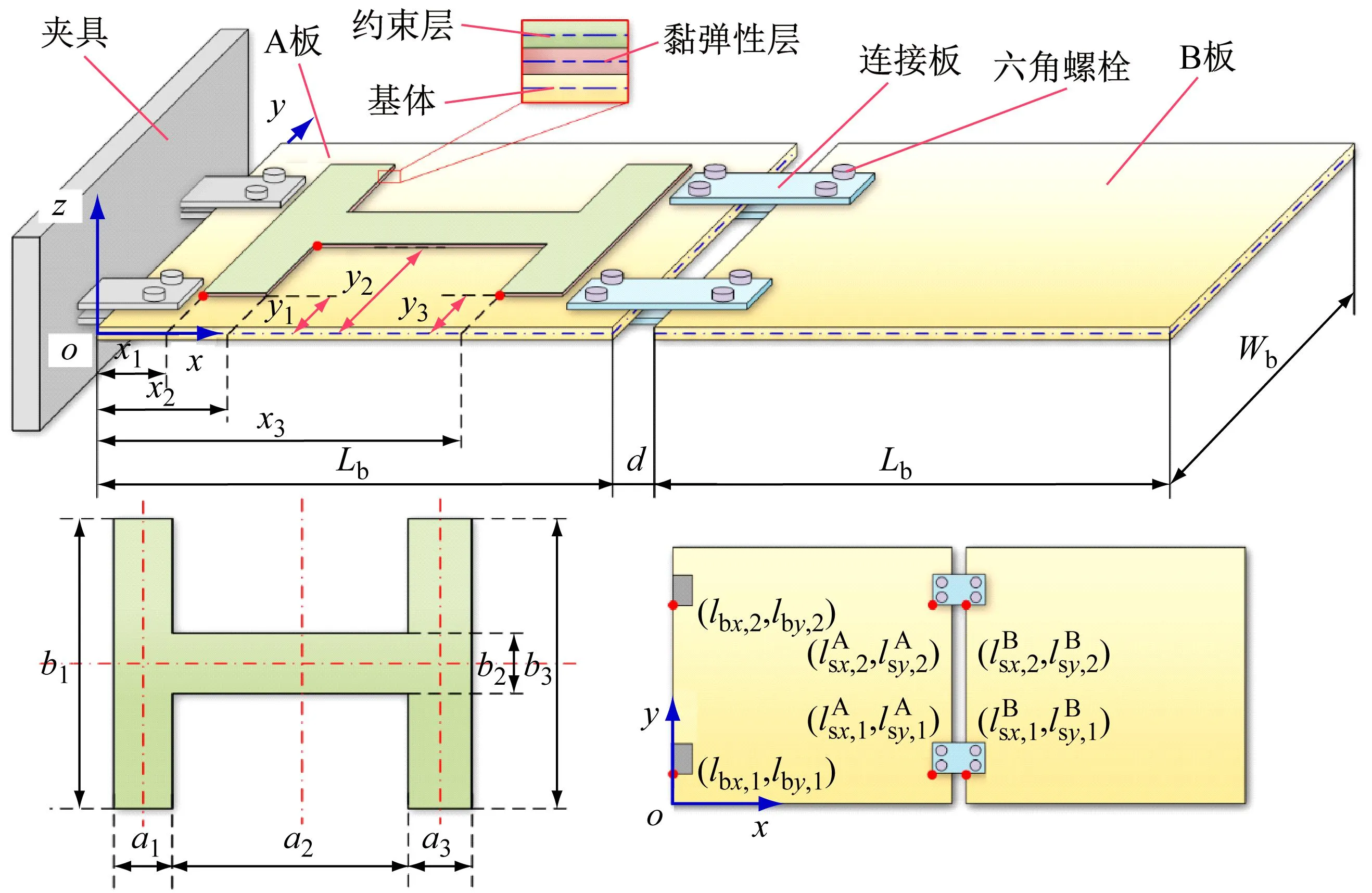
图2 贴敷“H型”约束阻尼层的双搭接螺栓连接薄板的结构示意图
1.3 局部贴敷约束阻尼层薄板的能量分析
对于贴敷“H型”约束阻尼层的A板,可以将基板和约束层分别利用Kirchhoff板理论假设位移函数。因此基板和约束层板内任意一点的位移可以表示为
(1)
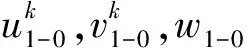
进一步利用几何方程,基板和约束层的任意一点的应变可表示为
(2)
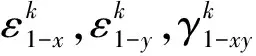
约束阻尼层复合结构由黏弹性层和约束层构成,由于约束阻尼层中黏弹性层受力后主要产生剪切变形,各层之间的变形示意图如图3所示。
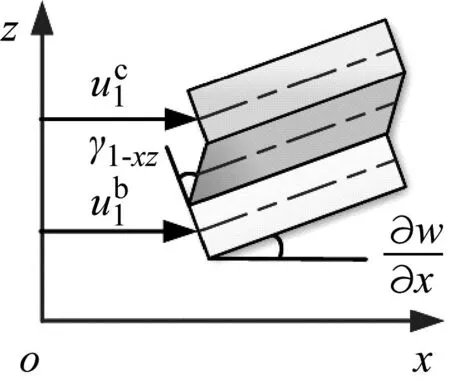
(a) x-z平面内变形
因此对于约束阻尼层结构中的黏弹性层仅考虑其在x-z和y-z平面内的应变[21],根据层间剪切变形原理可以得到
(3)
(4)
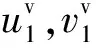
根据广义胡克定理可以得出基板和约束层的应力与应变的关系,具体为
(5)
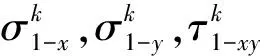
为了精确地描述约束阻尼层结构的振动特性,因此需要考虑材料的阻尼,可以用复弹性模量来描述。由于黏弹性材料损耗因子远大于基板以及约束层的材料损耗因子,故这里忽略基板和约束层的材料损耗因子,仅考虑黏弹性材料的损耗因子,用复弹性模量表示为
(6)
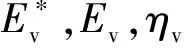
黏弹性层的应力应变关系可以表示为
(7)
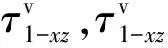
对于A板应变能主要包括基板和约束层的面内横向弯曲产生的剪切以及拉伸应变能量,以及黏弹性层的剪切应变能量,可以表示为
(8)
式中:ξ=1,2,3为第ξ块约束阻尼层;P1,P2,P3为中间变量。可以表示为
(9)
(10)
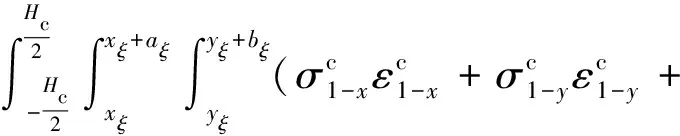
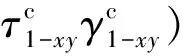
(11)
同时A板的动能可以表示为
(12)
式中,Q1,Q2,Q3为中间变量,可以表示为
(13)
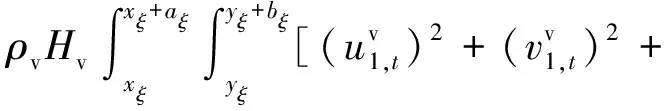
(w1,t)2]
(14)
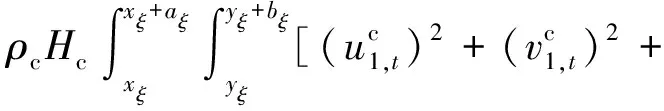
(w1,t)2]
(15)
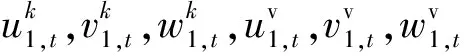
对于不贴敷约束阻尼层的B板,其应变能主要由基板的面内的弯曲剪切以及拉伸应变能量构成,动能主要由基板构成,可以表示为
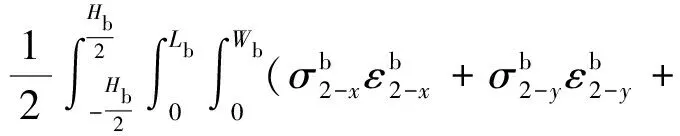
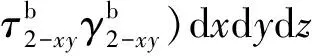
(16)
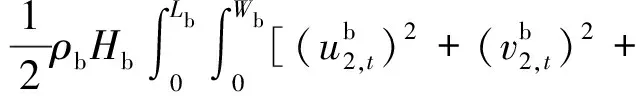
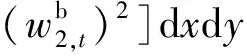
(17)
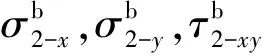
1.4 双搭接螺栓结合部和边界的能量分析
A板和B板被两个双搭接螺栓连接在一起,整个结构左端由夹具固定,整体处于一种悬臂状态,这里的夹持边界属于弹支边界条件,如图4所示。
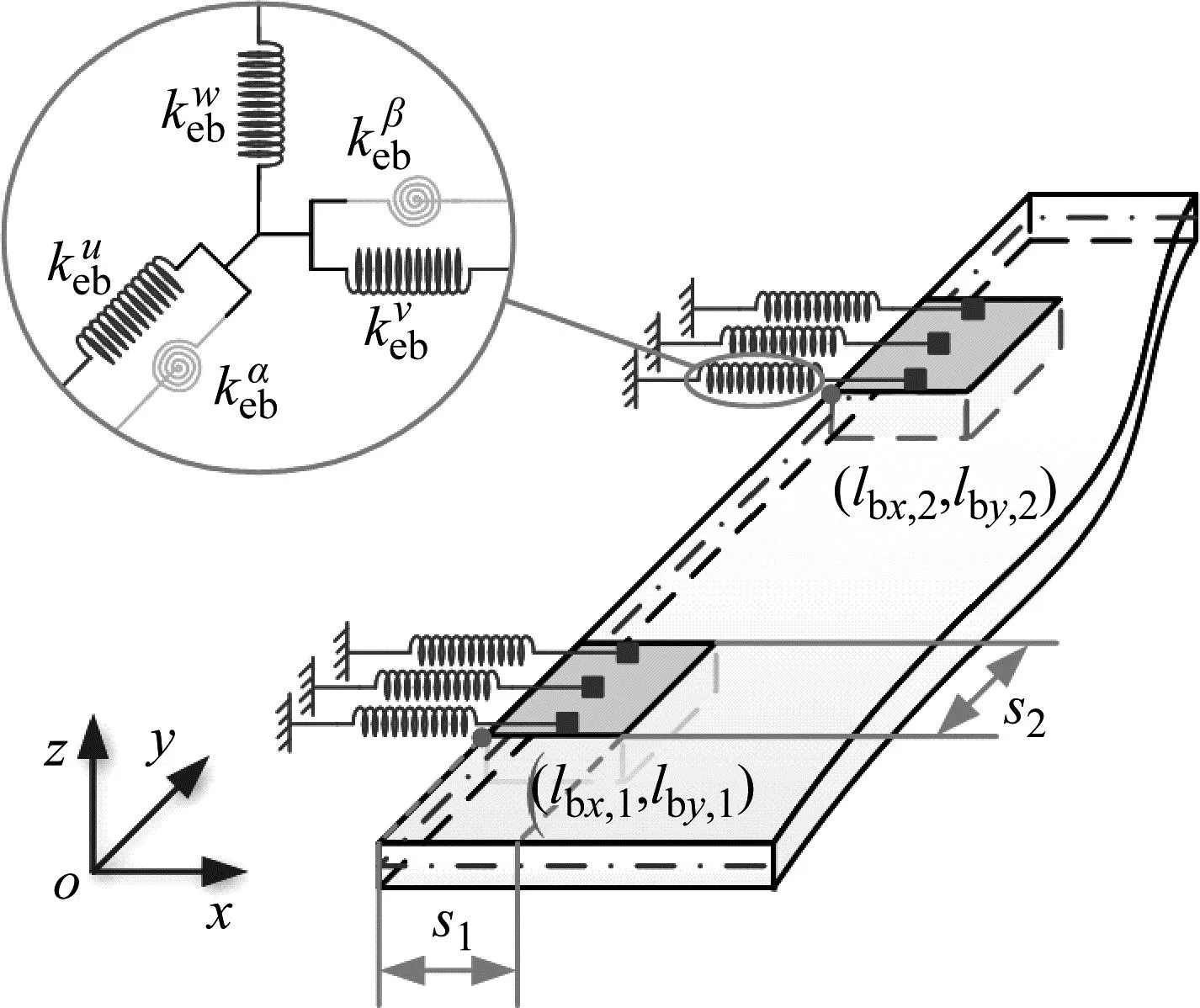
图4 弹簧模拟夹持边界条件示意图
被夹持的弹性边界条件可以用人工弹簧模拟[22],因此考虑在A板边界上的两个矩形夹持区域内施加虚拟的人工面弹簧。两个矩形区域面积相同,长宽为s1和s2,则弹支边界的势能可以表示为
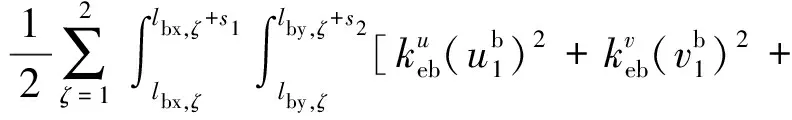
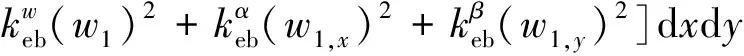
(18)
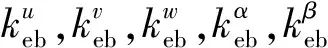
参见图5(a),考虑到连接两块板的双搭接螺栓结构中每两个螺栓的距离都很近,两个螺栓的影响区会有重叠区域,因而这里将每组双搭接双螺栓结合部在基板上产生影响区域近似成一个长宽分别为d1和d2矩形区域。同样在矩形区域施加人工面弹簧,但不同于上述边界的模拟,这里的弹簧刚度是复数,其不仅模拟了连接刚度还包括结合部产生的阻尼效应。此外,还需要考虑双搭接螺栓结合部带来的质量影响,这里用质量块模拟(见图5(b))。综上,创建完成了双搭接螺栓结合部的力学模型。
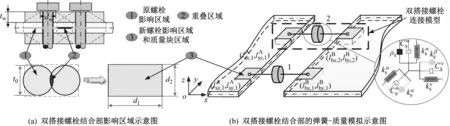
图5 双搭接螺栓结合部结构和弹簧-质量模拟的示意图
进一步,根据A板和B板的位移可以得到建立的双搭接螺栓连接模型的势能和动能,分别表达为
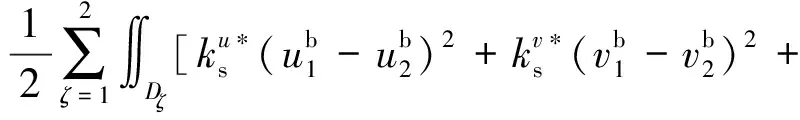
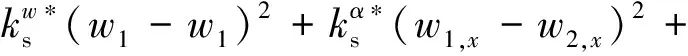
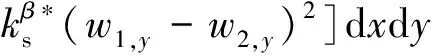
(19)
(20)
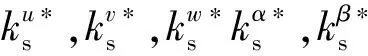
(21)
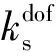
此外,对于双搭接螺栓结合部的参数可以通过对未贴敷约束阻尼层的双搭接螺栓连接板进行测试,并利用反推辨识得到[23-24]。
1.5 建立运动方程
将A板及B板的应变能和边界及双搭接螺栓的势能组合在一起可得到系统总的势能U,同理也可得到系统总的动能,总能量的表达式为
U=U1+U2+Uep+Ubolt
(22)
T=T1+T2+Ts
(23)
以下利用上述能量表达以及假设模态法,推导贴敷约束阻尼层的双搭接螺栓连接薄板的运动方程。
假设自由状态下A板做谐振运动,对应各自由度的位移容许函数可以表示为
w1(x,y,t)=Φ1(x,y)eiωt
(24)
式中:Φ1,Ψ1,Ω1为A板中对应基板自由度的自由振动振幅;Π1,Θ1为A板中对应约束层自由度的自由振动振幅;ω为自由振动频率。
为了便于求解,这里的自由振动振幅可以写成无量纲的正交多项式形式,对于基板令α=x/Lb,β=y/Wb,对于约束层令ϑ=x/Lv,υ=y/Wv,则有
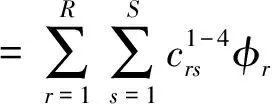
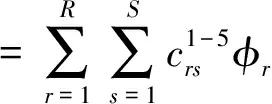
(25)
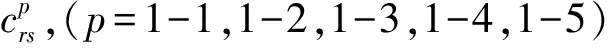
式中φr(α),φs(β)可以利用如下迭代公式[25]进行求解
φ1(χ)=1
φ2(χ)=(χ-G2)φ1(χ)
φm(χ)=(χ-Gm)φm-1(χ)-Hmφm-2(χ)
(26)
式中,χ=α,β,ϑ,υm≥2,其中,
(27)
对于φr(ϑ),φs(υ),也可做类似的处理。将上述求的正交多项式代入式可以得到关于α,β和ϑ,υ的Φ1,Ψ1,Ω1,Π1,Θ1无量纲振幅表达式。假如,要想获得有量纲的,可以再把α=x/Lb,β=y/Wb,ϑ=x/Lv,υ=y/Wv回代到式(25)中。
对于B板的位移容许函数也可进行类似式(24)的假设,只是不包含约束阻尼层部分,同样也可利用形如式(25)的正交多项式得到无量纲的表达,这里不再展开描述。
假定在A板上作用有频率为ω0的谐波点激励F0,激振点为(xe,ye),激振力可表达为
F0=F0eiω0tδ(x-xe)δ(y-ye)
(28)
这里,
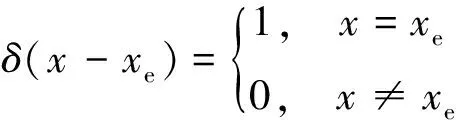
(29)
进一步,外力F0做的虚功可以表示为
(30)
最后,设L=T-U,利用拉格朗日方程并根据Hamilton原理的基本表达式
(31)
将用正交多项式表达的势能和动能(对应式(22)、(23))和式(30)代入式(31)中,整理可得贴敷约束阻尼层双搭接螺栓连接板在外部激振力下的振动方程,表示为
(K*-ω2M)X=F
(32)
式中:K*和M为整个系统的复刚度矩阵和质量矩阵(具体表达式见附录A和B);X为响应向量;F为外部的激振力向量。具体为
(33)
F=[F0Φ1(xe,ye)0000000]T
(34)
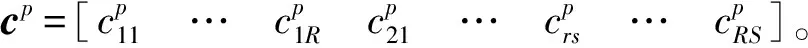
需要说明的是这里的复刚度矩阵K*的虚部是由黏弹性层的材料阻尼和螺栓结合部的结构阻尼构成。
2 振动参数求解
以下基于推导获得的贴敷约束阻尼层的双搭接螺栓连接薄板的运动方程式(32)求解固有频率、模态振型、模态损耗因子和频域振动响应等振动参数。
(1) 固有频率及模态振型
在自由振动状态下,外部作用力F为0,整理可得贴敷约束阻尼层的双搭接螺栓连接板在自由状态下的振动方程,表示为
(35)
通过式(35)求解可以得到双搭接螺栓连接板的第n阶固有频率ωn和特征向量φn。
将自由振动状态下得到的系数cp代入式(25)可以得到各自由度方向的模态振型函数。由于这里仅考虑获得z方向上的模态振型,因此求得振幅表达式Φ1(x,y)和Φ2(x,y)即可。取合适的多项式精度即R,S的值可得到模态振型表达式,
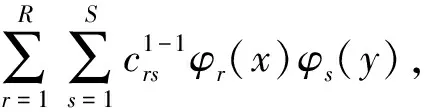
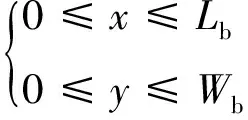
(36)
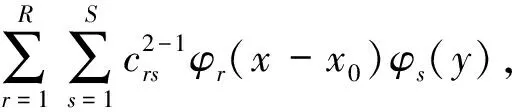
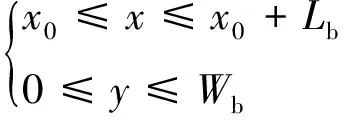
(37)
式中,Φ1和Φ2表示A板和B板z轴方向的模态振型函数,变量x0=Lb+d。
(2) 模态损耗因子
利用自由振动方程的特征向量φn,进而可以得到局部贴敷约束阻尼层的双搭接螺栓连接板各阶次的模态损耗因子,具体为
(38)
式中:ηn为第n阶的模态损耗因子;KI,KR为系统总刚度矩阵的虚部和实部。
(3) 频域振动响应
由式(32)可获得任意谐波激振力F0作用下的正交多项式待定系数向量,表达为
(39)
这里将待定系数向量X中对应z轴自由度方向的系数和拾振点坐标(xp,yp),代入到式(36)和(37),可得到在激振力F0作用下z方向上的频域振动响应。
3 实例研究
3.1 问题描述
本部分以图6所示的局部贴敷“H型”约束阻尼层的双搭接螺栓连接薄板为例,实践所研发的半解析建模方法,并通过组建试验系统证明了所建模型的合理性。试验件的材料参数和部分几何参数如表1所示。该结构中基板为环氧树脂,黏弹性阻尼层为ZN-1,约束层为铝箔。
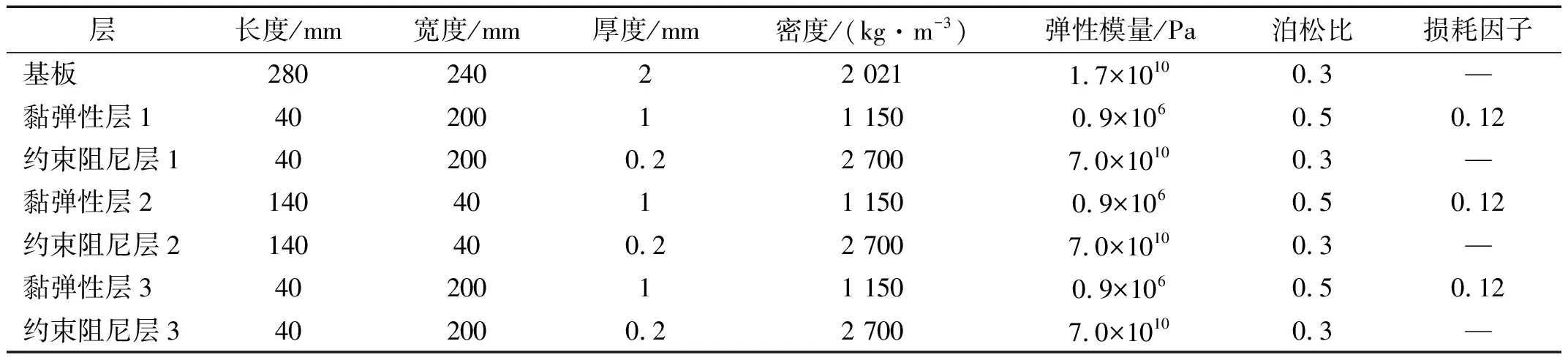
表1 双搭接螺栓连接薄板的相关材料参数及几何参数
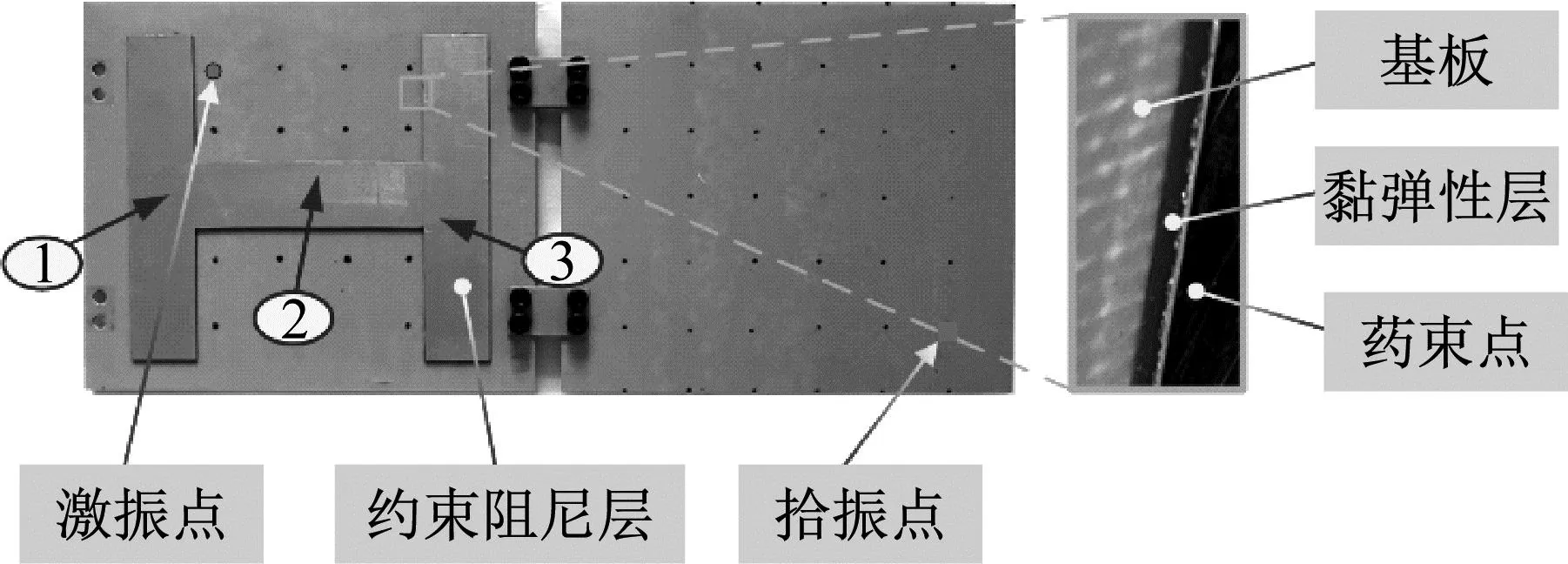
图6 贴敷“H型”约束阻尼层的双搭接螺栓连接薄板
为了完成半解析建模并校对模型的合理性,需要搭建可以获得贴敷“H型”约束阻尼的双搭接螺栓连接薄板固有特性和振动响应的试验系统,如图7所示。该试验系统主要包括联能JZK-5柔性杆激振器、PCB SN 30272模态力锤、KEYENCE IL-600激光位移传感器、PCB-208C04力传感器、SINOCERA YE8572A功率放大器、LMS SCSDAS数据采集前端和LMS.Testlab笔记本工作站等。后续将对贴敷约束阻尼层前的光板进行振动测试,获得的数据用于辨识模拟连接板夹持边界及双搭接螺栓结合部弹簧单元的参数。进一步,对贴敷“H型”约束阻尼的双搭接螺栓连接薄板进行测试,获得的数据用于校验半解析模型的合理性。

图7 贴敷“H型”约束阻尼层的双搭接螺栓连接板动力学特性测试系统
3.2 固有特性分析
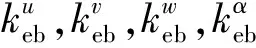
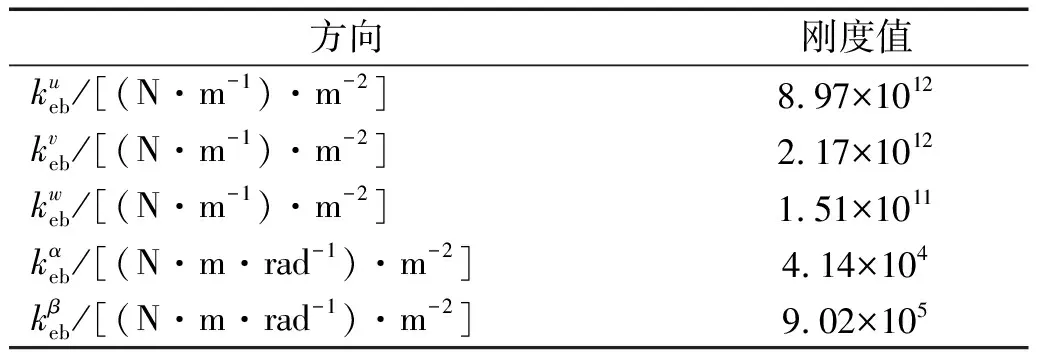
表2 基于反推辨识得到的模拟双搭接螺栓连接边界的弹簧刚度值

表3 基于反推辨识得到模拟双搭接螺栓连接的弹簧刚度值及阻尼值
根据建立的半解析模型可以得到结构的固有特性,具体为:通过式(35)可以获得贴敷约束阻尼层结构的固有频率,其与试验测得的固有频率对比如表4所示。通过式(36)和(37)可得到结构的模态振型,将基于半解析模型获得的模态振型与试验测得的结果进行对比如表5所示。从上述比对可以看出基于半解析模型获得的前5固有频率与试验结果最大偏差为4.74%,而模态振型基本一致,从而可认为所创建贴敷“H型”约束阻尼的双搭接螺栓连接薄板结构半解析模型在求解固有特性方面是合理的。需要说明的是这里并没有给出半解析模型获得的模态损耗因子与试验值比对,这主要源于当前基于半功率带宽法的阻尼测试方法与半解析模型计算中引入的阻尼层材料及结合部阻尼在机理上并不匹配,导致两者相差较大。但是由式计算出的模态损耗因子可以与频域响应相结合共同评估约束阻尼层对双搭接螺栓连接板结构的减振效果。
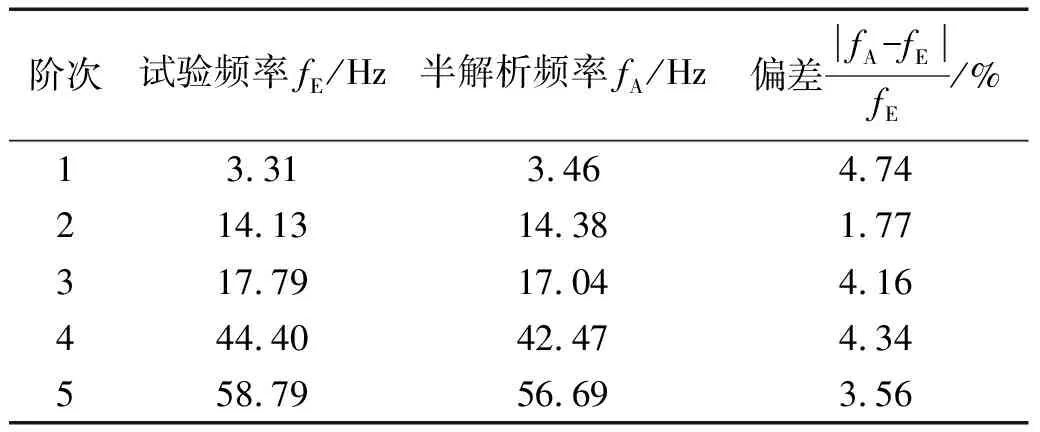
表4 贴敷“H型”约束阻尼层的双搭接螺栓连接板试验与基于半解析模型计算获得的前5阶固有频率

表5 贴敷“H型”约束阻尼层的双搭接螺栓连接板试验与基于半解析模型计算获得的前5阶模态振型
3.3 振动响应分析
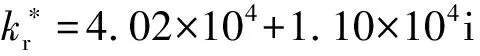
将上述模拟柔性杆力学特性的参数引入到建立的模型中,设定激振力为1 N,拾振点为(0.535 m,0.04 m),利用式(39)求解出前3阶贴敷“H型”约束阻尼层前后共振区的扫频响应,相关结果如表6和图8所示。
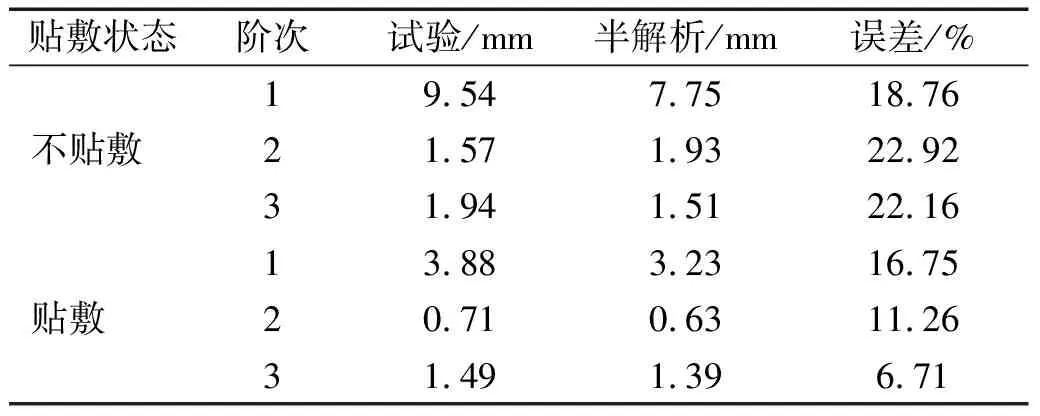
表6 贴敷“H型”约束阻尼层前后的双搭接螺栓连接薄板1 N激振力下试验与基于半解析模型计算获得的共振响应对比
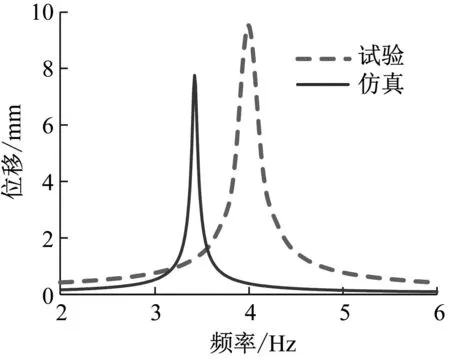
(a) 第1阶不贴敷约束阻尼层
从表6可以看出,贴敷约束阻尼层前后利用半解析模型的求解响应的最大偏差分别为22.92%和16.75%,从图8中可以看出利用半解析模型求得的响应曲线变化趋势基本与试验结果一致。另外,可以发现图8(a)第1阶未贴敷CLD的双搭接螺栓连接薄板的振动响应与试验值的误差大于图8(c)贴敷CLD板。之所以出现这一现象原因在于对于本结构贴敷CLD后1阶固有频率会相较于光板变大,因而会弥补基于光板参数辨识产生的误差,从而出现了贴敷CLD连接板结构相比较于光板,理论计算与实测值偏差更小的情况。从试验的角度来看,贴敷CLD可以使得双搭接螺栓连接薄板的第1阶共振响应下降59.32%;第2阶共振响应下降54.77%;第3阶共振响应下降23.19%,说明贴敷“H型”CLD层具有一定的减振效果。
综上,说明本文建立的局部贴敷CLD的双搭接螺栓连接薄板的半解析模型也可以预测复合结构的振动响应。
4 参数影响分析
以下基于所创建的贴敷“H型”约束阻尼层双搭接螺栓连接板结构的半解析模型分析阻尼层的贴敷面积及厚度对复合结构振动特性的影响。
(1) 约束阻尼层贴敷面积的影响
在此参数影响分析中其他参数与第3部分相同,仅改变“H型”约束阻尼层的面积。参见图9,“H型”约束阻尼层的中心位置(x0,y0)不变,通过改变3块约束阻尼层层的宽度a0来改变贴敷面积,设定的值分别为:0,10 mm,20 mm,30 mm,40 mm,50 mm,60 mm。对应贴敷率为:0,8.48%,16.67%,24.55%,30.95%,39.43%,46.43%。利用建立的半解析模型分别求解在1 N激振力下包含前3阶的共振区的频域响应,如图10所示。
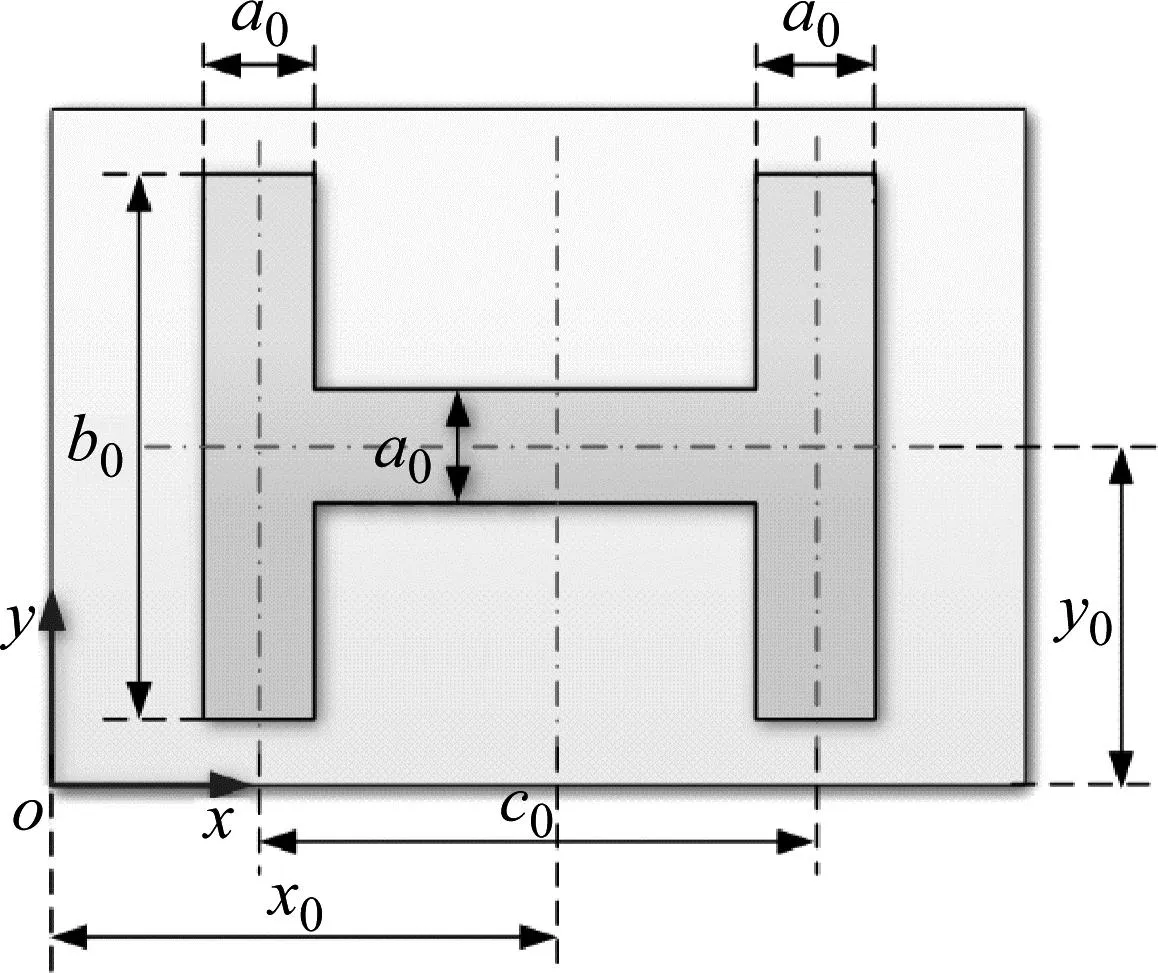
图9 “H型”约束阻尼层贴敷示意图
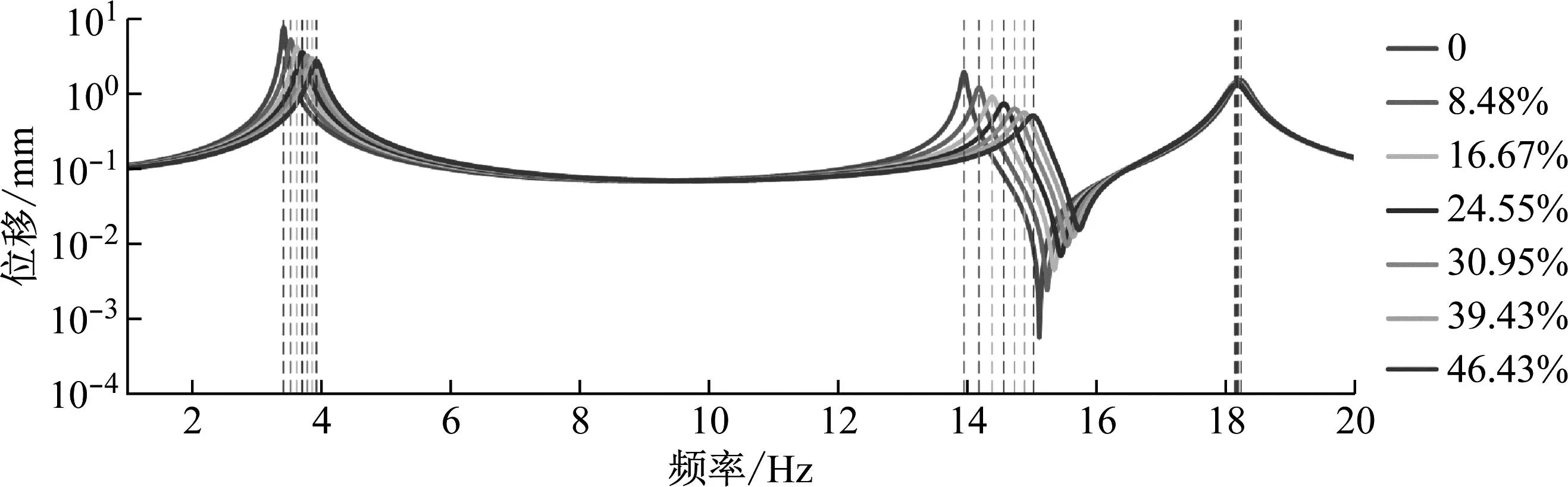
图10 不同约束阻尼层贴敷率的双搭接螺栓连接板在1 N激振力下的前3阶响应曲线
从图10中可以看出,随着贴敷率的增加,第1阶和第2阶的共振响应明显地逐渐减小,而第3阶变化不明显。但是随着贴敷率的逐渐增大,结构的共振频率逐渐增大,贴敷的约束阻尼层对结构的固有特性影响变大。
(2) 约束阻尼层的厚度的影响
这里同样保持其他参数与第3部分相同,而仅改变约束阻尼层中黏弹性层及约束层厚度,分析上述厚度参数对双搭接螺栓连接板减振效果的影响。首先设定约束层厚度为0.2 mm,改变黏弹性层的厚度为:0.5 mm,0.7 mm,0.9 mm,1.1 mm,1.3 mm,1.5 mm。利用建立的半解析模型求解模态损耗因子及在1 N激振力下前3阶共振区频域响应。接着,设定黏弹性层厚度为1.0 mm,改变约束层的厚度为:0.05 mm,0.15 mm,0.20 mm,0.25 mm,0.30 mm,同样执行上述求解。相关结果如图11~图13所示。
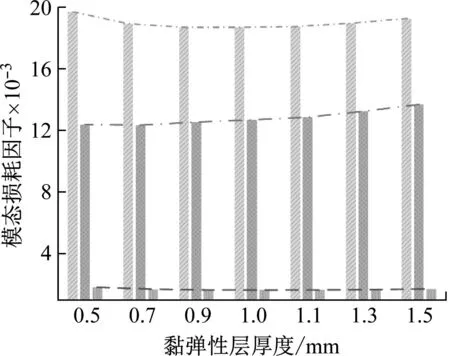
(a) 不同黏弹性层厚度
从图11(a)和图12可以看出,增加黏弹性层厚度对于所研究的双搭接螺栓连接板结构:第1阶和第3阶的共振响应先增大后减小,模态损耗因子先减小后增大;第2阶的共振响应逐渐减小,模态损耗因子逐渐增大。以上结果说明单纯增加黏弹性层厚度对于所研究结构并不一定能得到好的减振效果,对于第1及第3阶存在一个最优的厚度值使减振效果最好。
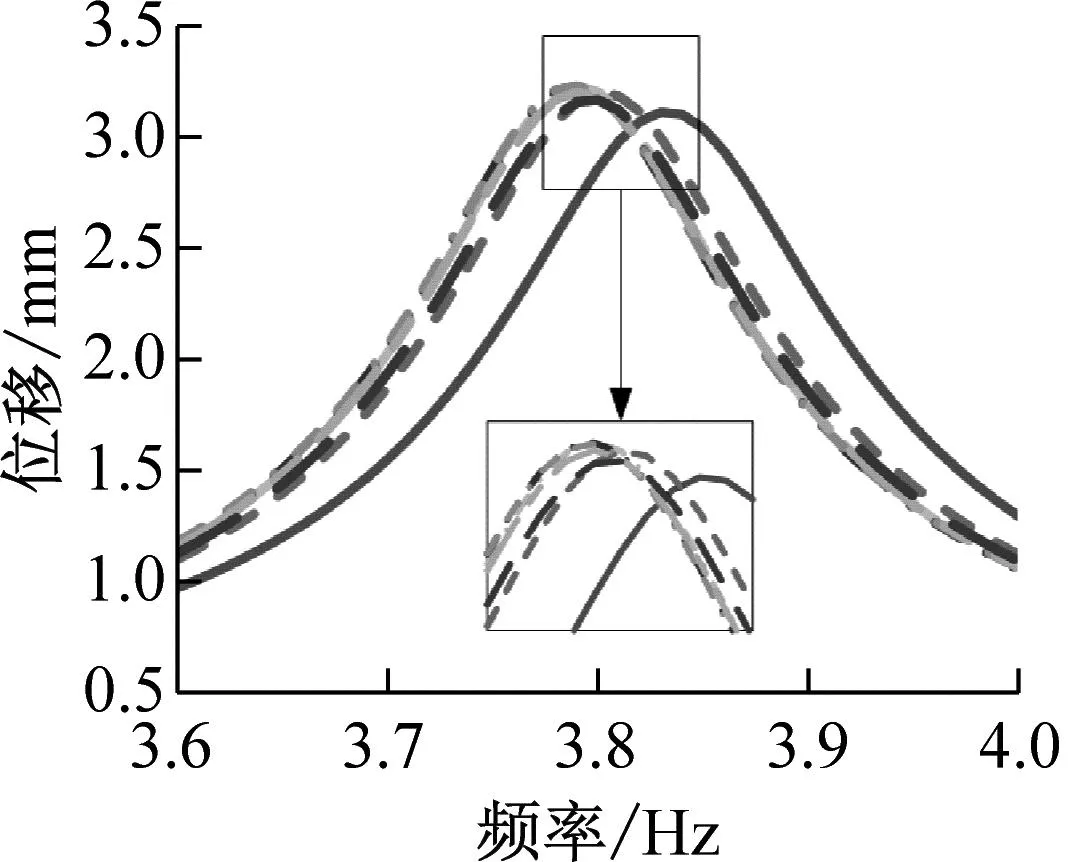
(a) 第1阶响应曲线
从图11(b)和图13可以看出,增加约束阻尼层厚度时,双搭接螺栓连接板前3阶的共振响应逐渐减小,模态损耗因子逐渐增大,说明对于本结构增加约束层厚度对减振总体上是有利的。但是同样的随着减振效果的提高,伴随着贴敷的约束阻尼层对结构的固有特性影响变大。
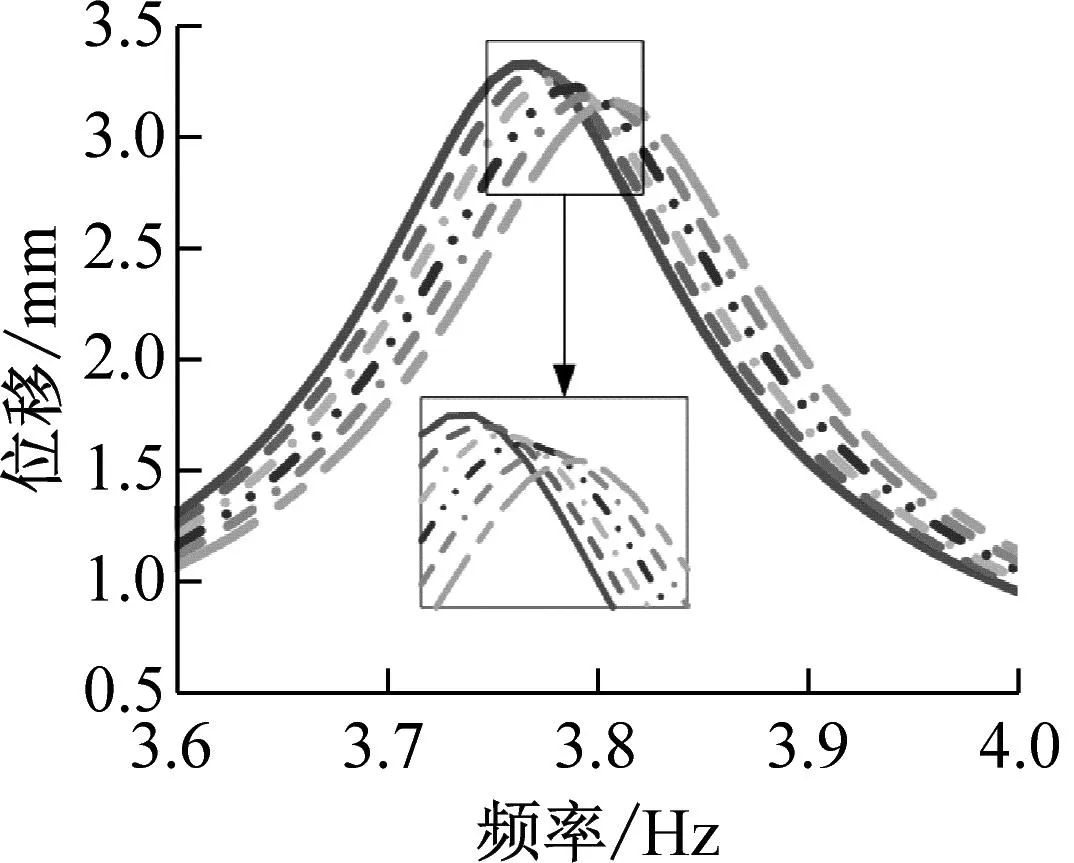
(a) 第1阶响应曲线
5 结 论
本文以模拟太阳翼帆板的双搭接螺栓连接板为对象,创建了局部贴敷“H型”约束阻尼层的双搭接螺栓连接板结构半解析动力学模型并进行了相关的减振分析,得出以下结论:
(1) 利用层间剪切变形原理建立贴敷“H型”约束阻尼层复合板的能量方程,考虑双搭接螺栓的影响区域,利用复面弹簧和修正质量模拟了双搭接螺栓结合部力学参数,建立了局部贴敷约束阻尼层的双搭接螺栓连接板的半解析分析模型,并给出了求解固有特性及振动响应的方法。实践表明所创建的动力学模型可有效模拟复合结构的动力学特性,基于半解析模型获得的前5阶固有频率与实测值最大偏差为4.74%,前3阶最大共振响应偏差为16.75%。
(2) 通过组建的贴敷“H型”约束阻尼层双搭接螺栓连接板试验系统以及相关的基于半解析模型获得结果,均表明约束阻尼层对双搭接螺栓连接板具有减振效果。具体为,贴敷后复合结构前3阶共振响应分别降了59.32%,54.77%,23.19%。
(3) 利用建立的局部贴敷约束阻尼层的双搭接螺栓连接板的半解析模型,分析了约束阻尼层的贴敷面积和贴敷厚度参数对所研究结构减振效果的影响,结果表明:随着贴敷面积的增加,总体上看结构的共振响应减小,因而可以说明增大贴敷面积对减振有利,但是对结构自身固有特性影响加大;单纯增加黏弹性层厚度对于所研究结构并不一定能得到好的减振效果,对于第1及第3阶存在一个最优的厚度值使减振效果最好;增加约束层厚度时,总体上看对减振是有利的,但是同样存在对结构自身固有特性影响变大的情况。
(4) 需要说明的是本文以“H型”贴敷约束阻尼层为例,主要研究局部贴敷约束层的双搭接螺栓连接板半解析动力学建模问题。为了更好地实施约束阻尼层减振,还需研究不同的阻尼层贴敷方案对双搭接螺栓连接板减振的影响,并获得最佳的阻尼层贴敷方案,即研究双搭接螺栓连接板结构约束阻尼层结构拓扑优化的问题。
附录A
局部贴敷约束阻尼层的双搭接螺栓连接薄板的刚度矩阵可以表示为
(A.1)
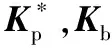
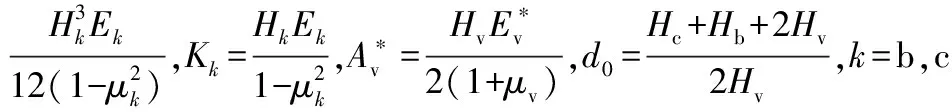
(A.2)
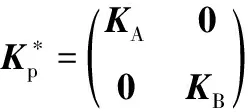
(A.3)
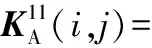
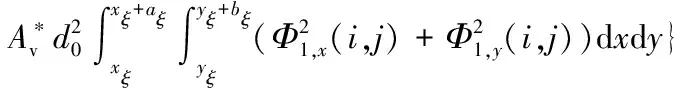
(A.4)
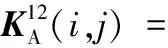
(A.5)
(A.6)
(A.7)
(A.8)
(A.9)
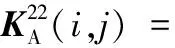
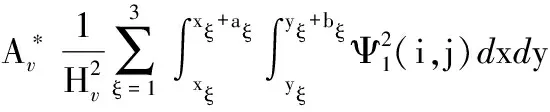
(A.10)
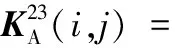
(A.11)
(A.12)
(A.13)
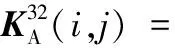
(A.14)
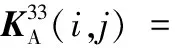
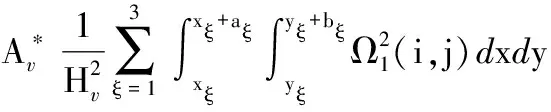
(A.15)
(A.16)
(A.17)
(A.18)
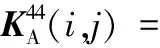
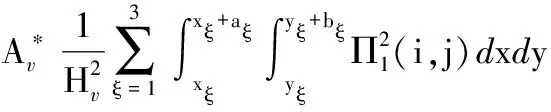
(A.19)
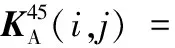
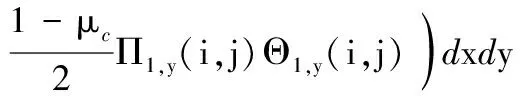
(A.20)
(A.21)
(A.22)
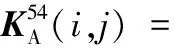
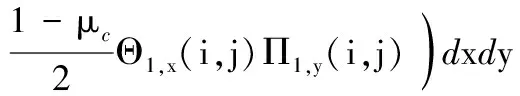
(A.23)
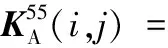
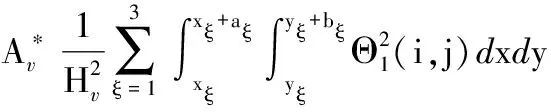
(A.24)
(A.25)
令aξ=bξ=0代入KA可得到KB。
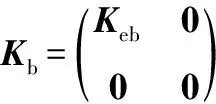
(A.26)
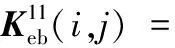
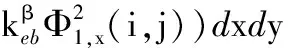
(A.27)
(A.28)
(A.29)
(A.30)
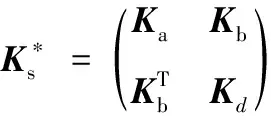
(A.31)
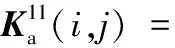
(A.32)
(A.33)
(A.34)
(A.35)
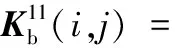
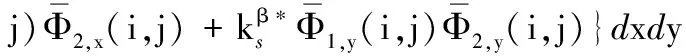
(A.36)
(A.37)
(A.38)
(A.39)
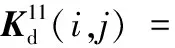
(A.40)
(A.41)
(A.42)
(A.43)
其中,
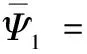
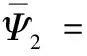
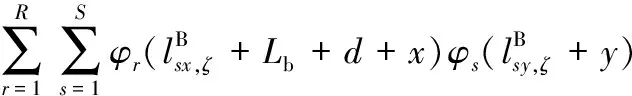
(A.44)
附录B
局部贴敷约束阻尼层的双搭接螺栓连接薄板的质量矩阵可以表示为
M=Mp+Ms
(B.1)
式中,Mp,Ms为贴敷约束阻尼层薄板的质量矩阵和双搭接螺栓连接弹簧的质量矩阵。
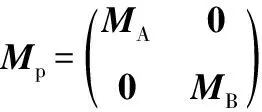
(B.2)
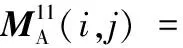
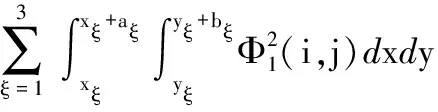
(B.3)
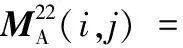
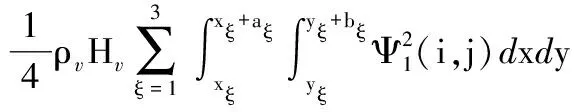
(B.4)
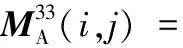
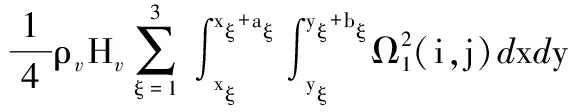
(B.5)
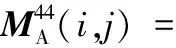
(B.6)
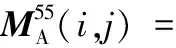
(B.7)
同理,令aξ=bξ=0代入MA可得到MB。
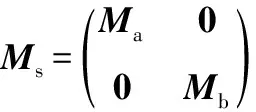
(B.8)
(B.9)
(B.10)
(B.11)
(B.12)

