弹性环式挤压油膜阻尼器一体化圆柱滚子轴承保持架振动特性分析

王树涵,杨海生,唐 瑞,罗 斌,杨小民,邓四二

(1.河南科技大学 机电工程学院,洛阳 471003;2.中国航空发动机集团有限公司 四川燃气涡轮研究院,成都 610500)

新一代航空发动机的研制除了向高推重比、高性能等方向发展外,还对结构、工况等方面提出更高的要求。为了降低转子过临界转速时产生剧烈振动,将弹性环、挤压油膜阻尼器与滚动轴承联合使用,形成弹性环式挤压油膜阻尼器(elastic ring squeeze film damper,ERSFD) 一体化圆柱滚子轴承,提高航空发动机?轴承系统的动态性能和工作可靠性。

弹性环式挤压油膜阻尼器一体化圆柱滚子轴承的动态特性研究已引起众多学者的关注。周明等[1-3]利用雷诺方程推导了ERSFD内外油膜压力控制方程,建立 ERSFD 减振机理模型,初步研究了其减振机理。洪杰等[4]基于有限元方法,根据有限元挤压油膜理论对ERSFD中的弹性环支承刚度、油膜压力场分布和油膜阻尼等特性进行了研究。曹磊等[5-6]通过对弹性环刚度和ERSFD油膜特性的研究,指出了 ERSFD 的减振机理,确定了影响转子临界转速的重要因素。Zhang等[7]采用有限微分法和数值模拟方法分析了ERSFD的油膜压力分布、承载能力、油膜刚度和振动期间的阻尼特性,并根据油膜压力结果,用有限元方法揭示弹性环的变形。王震林等[8-9]考虑弹性环凸台处的接触作用,采用数值方法改进了ERSFD的流固耦合模型,识别了油膜和弹性环的动力学特性,研究了涡动频率、凸台数目、高度和宽度以及弹性环厚度对阻尼器动力学特性系数的影响。Han等[10]利用SAM方法,通过将转子动力学方程与弹性变形的确定相结合,开发了一种改进的 ERSFD 支撑转子的动力学模型,指出采用ERSFD可以显著提高转子系统的等效油系数和阻尼比。Chen等[11]利用一种半解析法建立了一种带有ERSFD的螺旋锥齿轮模型,该模型可以很好的利用与齿轮系统,研究结果表明ERSFD与传统的挤压油膜阻尼器(squeeze film damper,SFD)相比,在抑制系统非线性特性方面具有更好的性能。Meeus等[12-13]通过试验对乏油状态下带SFD的圆柱滚子轴承进行研究,结果表明轴承在轻载工况下,不平衡激振升高时会出现高度非线性行为;随后通过试验模拟和测量振动响应,提出增加轴承受载有助于缓解转子振动问题。孙雪等[14]建立了考虑轴承套圈弹性变形因素的弹支高速圆柱滚子轴承动力学模型,分析了不同弹性支承结构参数和径向载荷、轴承内圈转速对保持架稳定性的影响,研究结果表明:与刚性支承相比,弹性支承使轴承保持架稳定性有了明显的提升。夏玉磊等[15]在非稳态工况下建立弹支 SFD 圆柱滚子轴承-刚性转子刚柔耦合动力学分析模型,对轴承打滑率进行了分析。李文洒[16]建立了鼠笼弹支挤压油膜阻尼器轴承圆柱滚子轴承模型,对鼠笼弹支SFD轴承振动特性及外圈质心轨迹进行分析,并通过试验对鼠笼弹支SFD对轴承减振作用进行了验证。郑向凯[17-18]利用刚柔耦合连接将鼠笼弹支结构与轴承外圈和轴承座相连接,建立鼠笼弹支一体化球轴承动力学模型,对轴承保持架打滑率进行分析,并在此基础上将模型与SFD进行耦合,研究了轴承工况参数对弹支 SFD 球轴承振动及保持架稳定性的影响。田野等[19]通过试验对带鼠笼弹支-挤压油膜阻尼器的滚动轴承进行研究,分析了弹支结构和SFD的刚度和阻尼特性,计算出该系统的临界转速和瞬态动力特性,试验结果表明,鼠笼弹支-SFD结构可以降低转子的最大振动幅值,提高系统稳定性。上述学者在进行ERSFD动力学性能分析时,均是将轴承简单等效为一个阻尼和弹簧刚度;在弹性环式挤压油膜阻尼器一体化圆柱滚子轴承动力学性能分析时,目前基本是鉴于弹支结构、挤压油膜阻尼器或弹性环式挤压油膜阻尼器单个因素基础上的圆柱滚子轴承动态特性分析,缺乏弹性环式挤压油膜阻尼器一体化的动力学特性与圆柱滚子轴承动态性能的相互影响研究。刘准等[20]对某型号航空发动机进行了模拟试验,出现了极少见的转子—轴承系统振动幅值长周期变化现象,根据此现象进行长时间测试和验证。试验表明,轴承游隙较大时造成了该轴承的振动幅值长周期变化现象。通过改变供油条件或适当增加不平衡载荷的方式消除该现象。田晶等[21]利用建立的中介轴承多点复合故障的4自由度动力学模型分析轴承故障的动力学特性;搭建试验台以采集振动信号,对动力学模型进行验证。鉴于此,本文在滚动轴承动力学理论基础上,结合ERSFD动力特性,建立了ERSFD一体化圆柱滚子轴承动力学分析模型,对ERSFD一体化圆柱滚子轴承保持架振动特性及打滑率进行分析,研究结果对弹性环式挤压油膜阻尼器一体化圆柱滚子轴承的结构设计提供一定的理论基础。

1 弹性环式挤压油膜阻尼器一体化圆柱滚子轴承动力学模型

1.1 弹性环式挤压油膜阻尼器一体化圆柱滚子轴承坐标系

根据弹性环式挤压油膜阻尼器一体化圆柱滚子轴承的结构特点,建立如图1所示的坐标系。

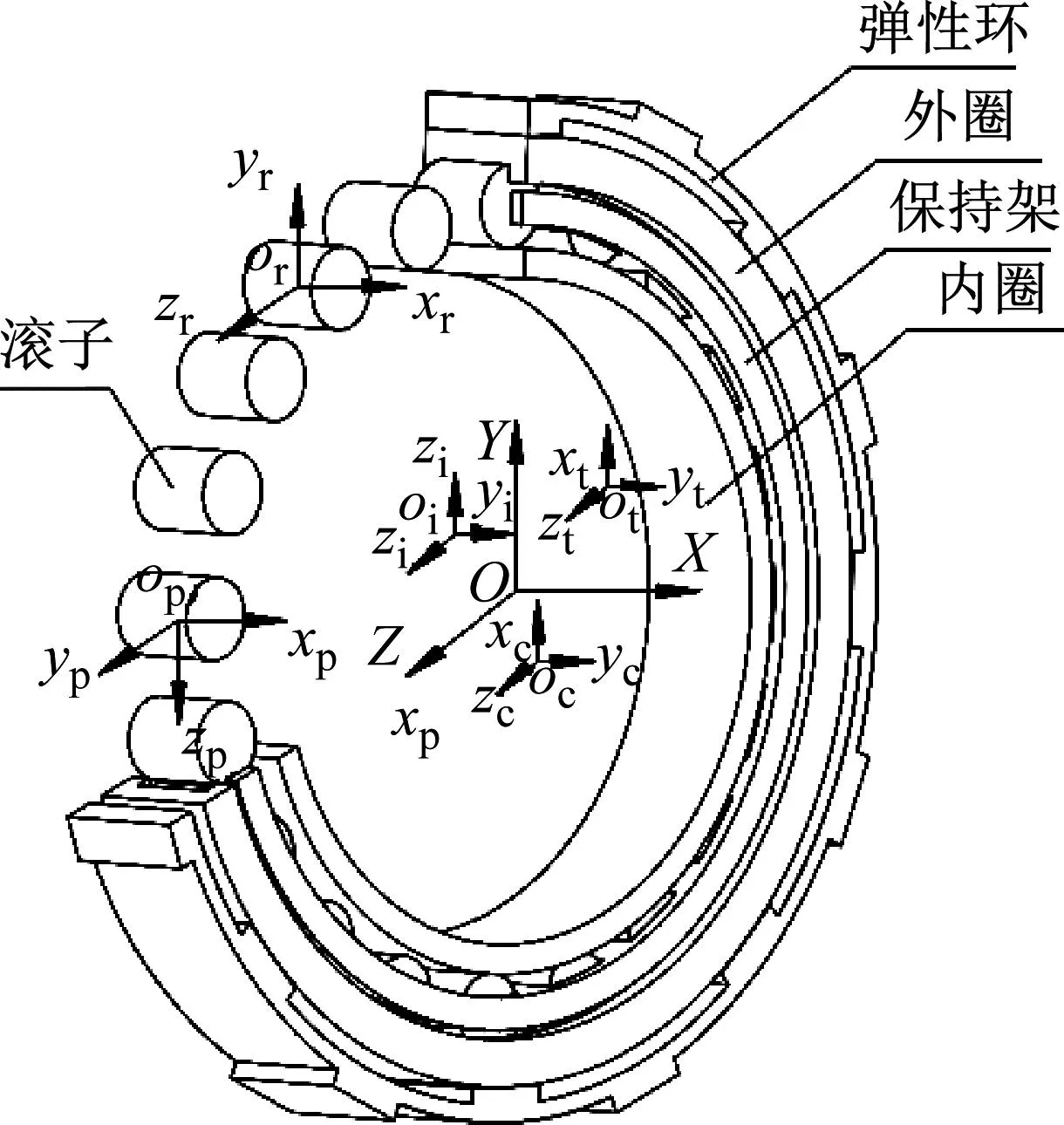
图1 弹性环式挤压油膜阻尼器一体化圆柱滚子轴承坐标系

(1) 惯性坐标系{O;X;Y;Z},X轴与轴承轴线重合,YOZ面与通过轴承中心的径向平面平行,此坐标系在空间中固定,其他坐标系均参照此坐标系来确定。

(2) 滚子质心坐标系{or;xr;yr;zr},此坐标系原点与滚子几何中心重合,yr沿轴承径向方向,zr沿轴承周向方向。此坐标系随着滚子中心移动,但不随滚子自转,每个滚子都有自己的局部坐标系。

(3) 保持架质心坐标系{oc;xc;yc;zc},此坐标系由惯性坐标系{O;X;Y;Z}平移得到,原点oc与保持架几何中心重合,坐标系随着保持架一起移动和旋转。

(4) 保持架兜孔中心坐标系{op;xp;yp;zp},此坐标系开始时与滚子质心坐标系重合,随后随着保持架一起移动和旋转;此坐标系的原点op与保持架兜孔几何中心重合,每个兜孔都有自己的局部坐标系。

(5) 内圈质心坐标系{oi;xi;yi;zi},此坐标系由惯性坐标系{O;X;Y;Z}平移得到,坐标原点oi与内圈几何中心重合,坐标系随内圈一起移动和旋转。

(6) 弹性环质心坐标系{ot;xt;yt;zt},此坐标系由惯性坐标系{O;X;Y;Z}平移得到,坐标原点ot与弹性环几何中心重合。

1.2 ERSFD计算模型

ERSFD一体化圆柱滚子轴承结构如图2所示。与传统的挤压油膜阻尼器(SFD)相比,ERSFD在挤压油膜中装配了弹性环结构,弹性环的内外侧交替布置支承凸台,将挤压油膜分隔成多个分段的油膜腔,内凸台与轴承外圈(轴颈)的外圆柱面接触,外凸台与轴承座的内圆柱面接触。

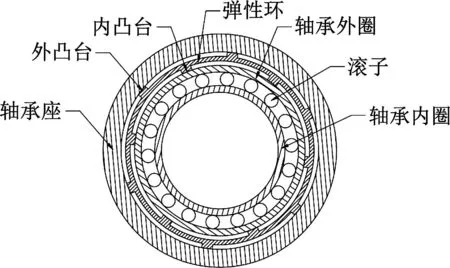
图2 弹性环式挤压油膜阻尼器一体化圆柱滚子轴承简图

弹性环相对轴承座不自转,阻尼器的长度与轴颈直径之比通常小于1/4,内外腔的油膜半径间隙通常不超过轴颈直径的千分之五。为了简化控制方程,本文忽略弹性环上的小孔,且阻尼器未有轴向端封,对油膜流体作以下假设:① 忽略体积力; ② 薄膜流动; ③ 流体为不可压牛顿流; ④ 未考虑温度效应和轴颈曲率效应;⑤ 沿润滑膜厚度方向黏度数值不变;⑥ 流体为层流流动;⑦ 忽略惯性力。

根据以上的假设并结合N-S方程,推导出弹性环式挤压油膜阻尼器的油膜控制方程为

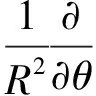
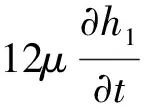
(1)

(2)

式中:μ为润滑油的黏度;R为轴颈半径;x和θ分别为轴向和周向坐标;Ω为轴颈进动速度;p1和p2分别为内外油膜油的压力;h1和h2分别为内外油膜厚度,取内油膜厚度h1=c1+ecosθ+r(θ),外油膜厚度h2=c2-r(θ),c1与c2为弹性环式挤压油膜阻尼器的内外油膜半径间隙,e为轴颈偏心距,r为弹性环径向变形量。

弹性环受轴颈的周期偏心距激励。假定轴颈作稳态圆进动,径向平面的位移表示为

xt=eosin(Ωt);yt=eocos (Ωt)

(3)

式中,eo为轴颈涡动半径。

将内凸台视为刚性结构并与轴颈的外圆柱面接触,外凸台与轴承座内环的接触视为固定约束,两者始终接触;因此弹性环上第i个凸台的径向位移为

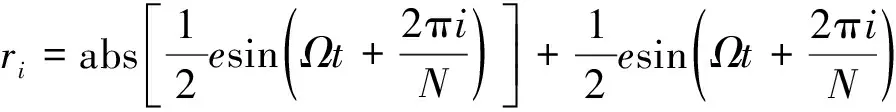
(4)

式中,i=1,2,…,N,N为弹性环凸台个数。

将式(1)与式(2)积分,推导出内外油压的表达式

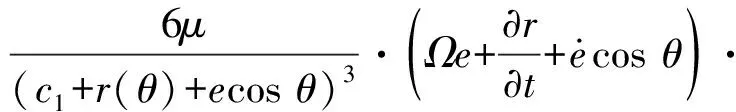
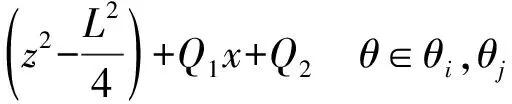
(5)

Q1x+Q2θ∈θi,θj

(6)

(7)

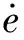
阻尼器轴向两端的边界条件为

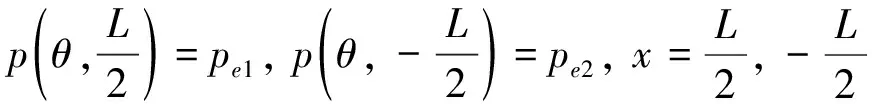
(8)

式中,pe1和pe2分别为阻尼器轴向初始压力。因为本文研究的为弹性环式挤压油膜阻尼器无密封的情况,所以初始压力为

p1(θ,z)=0;p2(θ,z)=0;θ∈θbi,θbj

(9)

式中,θbi和θbj分别为凸台位置的上下圆周角。

周向油膜力Fr和径向油膜力Fr可以通过对油膜压力(以内油膜为例)在下边界角至上边界角之间进行积分获得

(10)

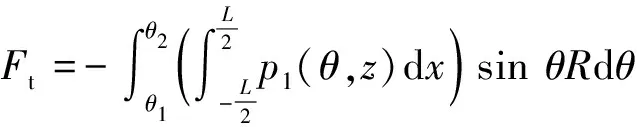
(11)

最后将弹性环式挤压油膜阻尼器作用在轴承外圈的油膜力转换到y和z方向可以表示为

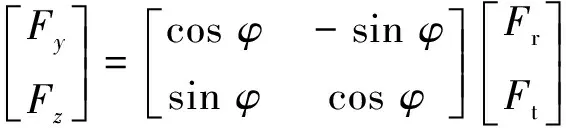
(12)

式中,φ表示轴承径向与z轴之间的偏移角。

1.3 弹性环刚度计算模型

传统的弹性环刚度经验公式只能对弹性环刚度进行近似的估计,因此,使用有限元方法计算弹性环刚度[22]。忽略弹性环的刚性运动,在弹性环内外侧建立两个刚性环分别模拟轴承外圈与轴承座内环。在模型外侧施加径向约束,并对弹性环上一排节点施加径向力,对这些节点施加周向和轴向约束;求解出弹性环变形量后,由下式计算出弹性环刚度

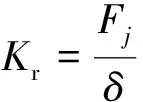
(13)

式中:Kr为弹性环刚度;Fj为施加的径向力;δ为弹性环最大位移量。

1.4 弹性环式挤压油膜阻尼器一体化圆柱滚子轴承动力学微分方程

1.4.1 滚子动力学微分方程

轴承运转过程中,轴承内、外圈、保持架等都对滚子产生相对作用,滚子受力如图3所示。本文采用“切片法”对滚子进行处理,计算滚子所受载荷[23]。

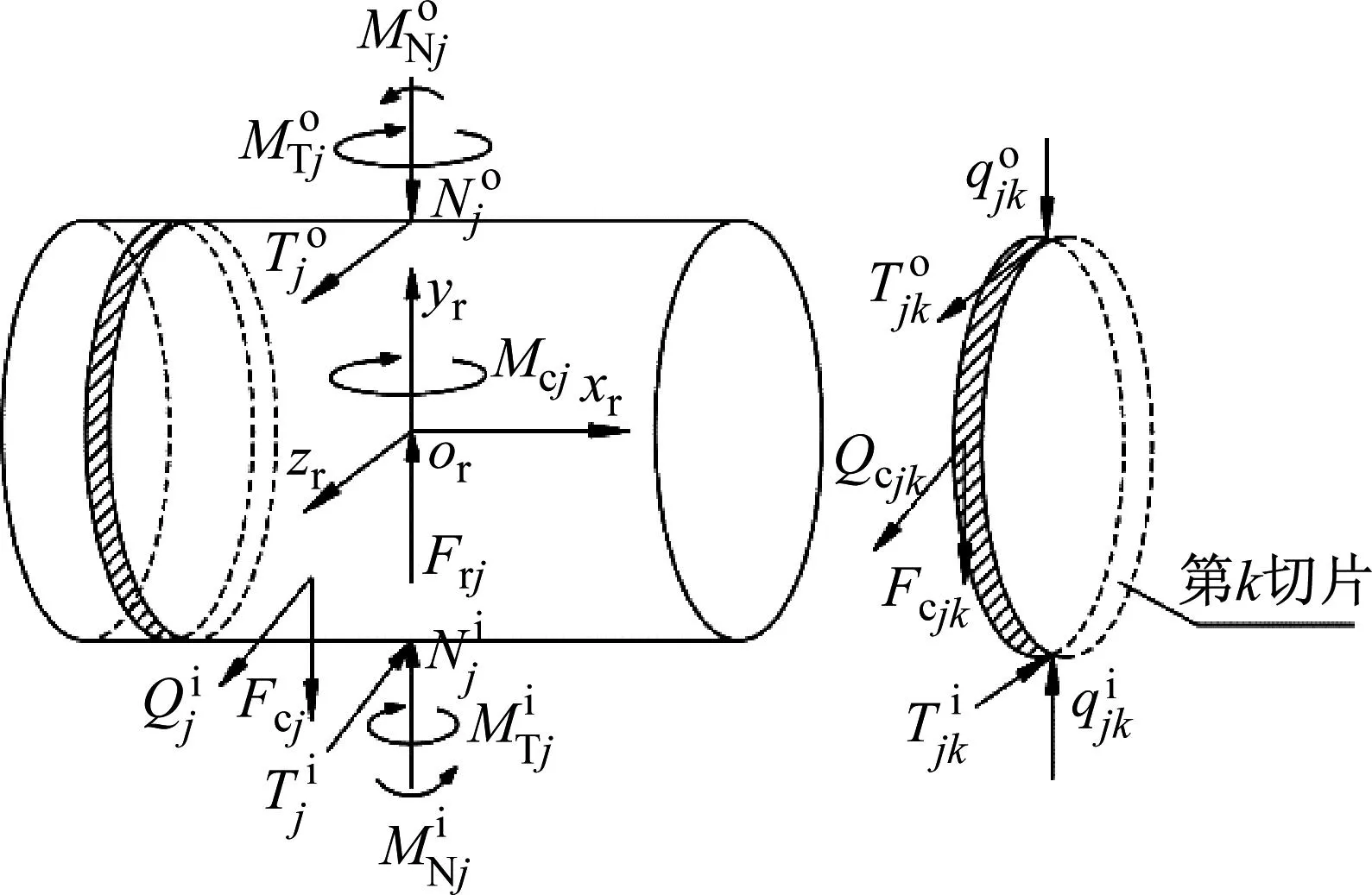
图3 滚子受力示意图

(14)

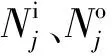
1.4.2 保持架动力学微分方程

轴承在运转过程中,其保持架受到滚子的碰撞摩擦力、保持架与引导面间滑油对保持架端面和表面阻力的共同作用,保持架的受力如图4所示。

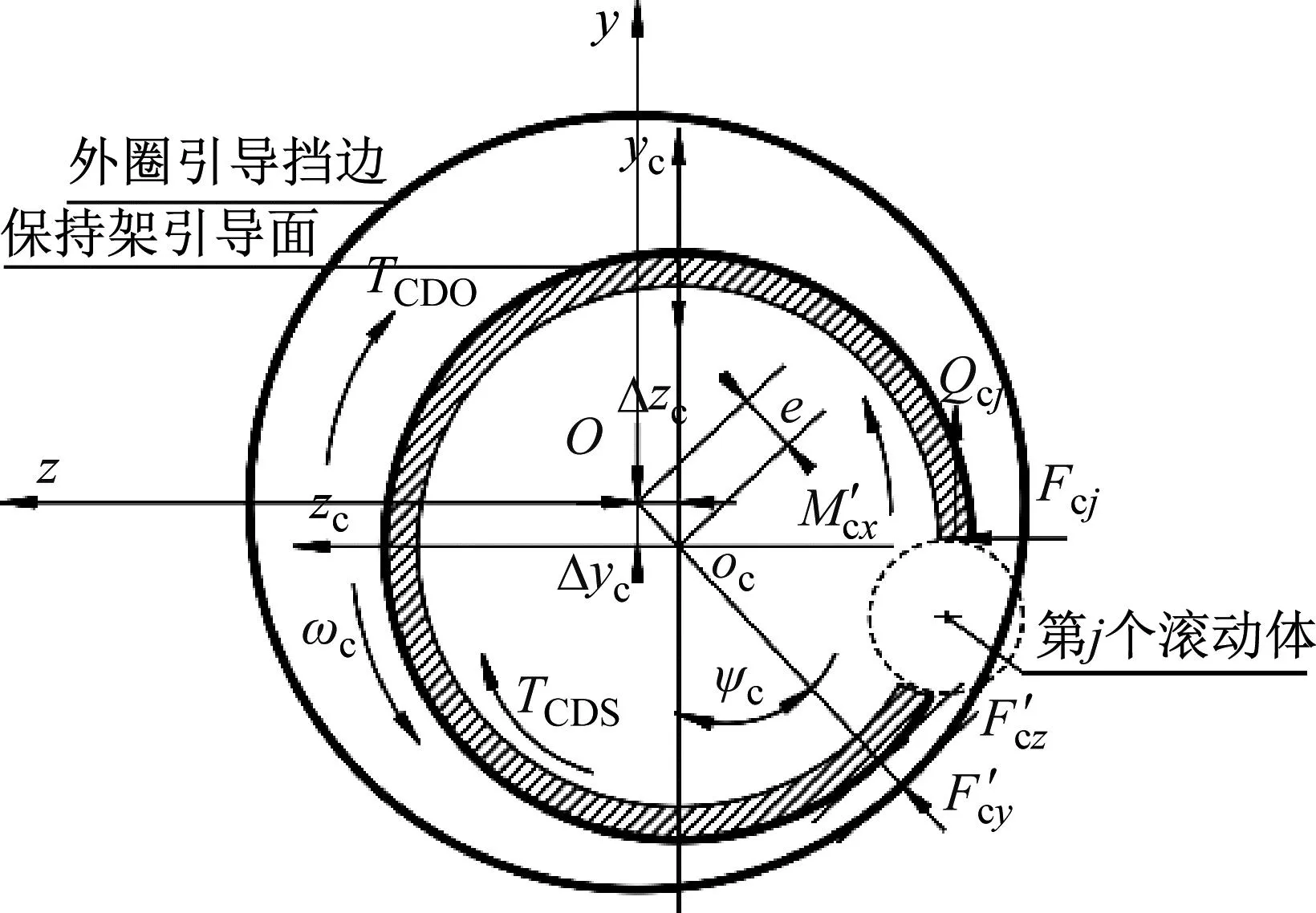
图4 保持架受力示意图

(15)

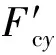
1.4.3 内圈动力学微分方程

内圈的动力学微分方程可表示为

(16)

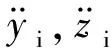
1.4.4 外圈动力学微分方程

轴承在运转时,外圈不发生转动,因此不需要建立轴承外圈力矩平衡方程。与弹性环式挤压油膜阻尼器结构耦合后轴承外圈受到弹性环自身支反力和挤压油膜阻尼器y和z方向的油膜力,耦合后的外圈动力学微分方程为

(17)

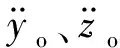
2 弹性环式挤压油膜阻尼器一体化圆柱滚子轴承保持架振动特性分析

以某航空发动机主轴圆柱滚子轴承为分析对象,采用GSTIFF预估-校正变步长积分法对弹性环式挤压油膜阻尼器一体化圆柱滚子轴承动力学方程组进行求解,研究轴承转速、载荷以及弹性环结构参数对弹性环式挤压油膜阻尼器一体化圆柱滚子轴承保持架振动特性以及保持架打滑率的影响。弹性环式挤压油膜阻尼器一体化圆柱滚子轴承主要参数如表1所示。

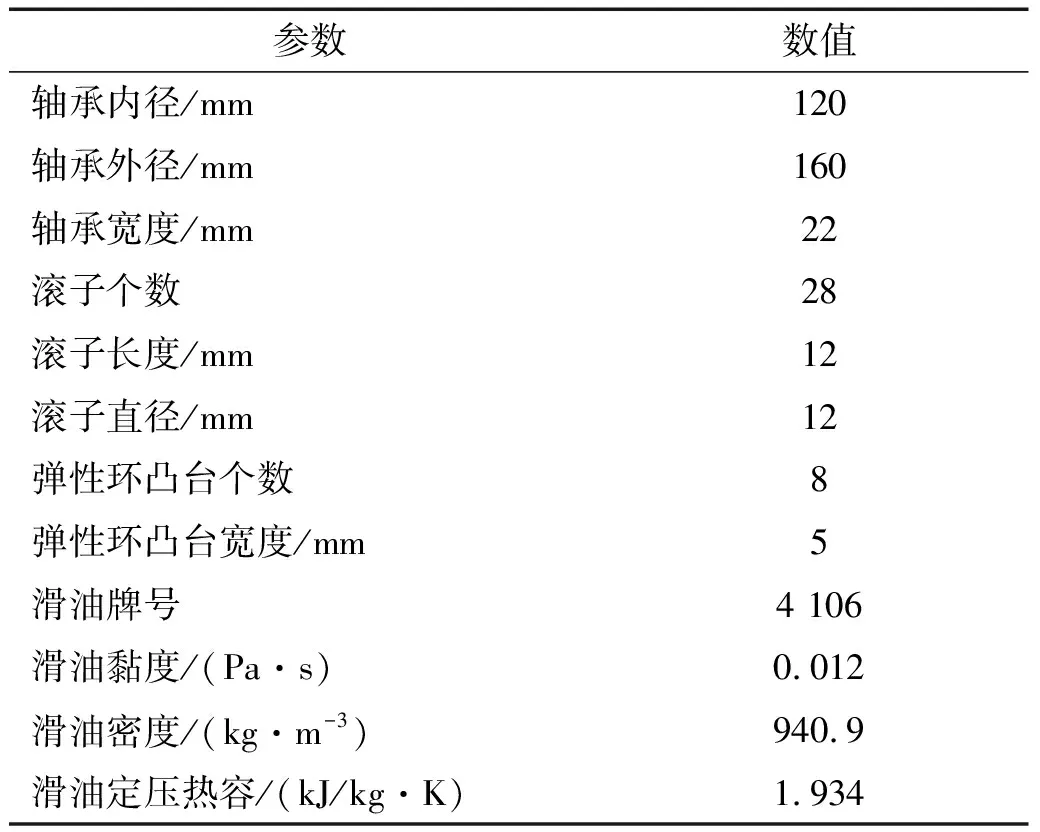
表1 弹性环式挤压油膜阻尼器一体化圆柱滚子轴承主要参数

对于圆柱滚子轴承,保持架打滑率定义为

(18)

(19)

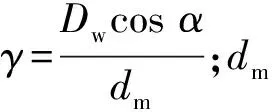
对振动加速度的时域图进行快速傅里叶变换,得到振动加速度的频谱图。振动加速度级为

(20)

式中:aRMS为振动加速度的均方根值,m/s2;a0为参考加速度,取a0=9.81×10-3m/s2。

2.1 转速对弹性环式挤压油膜阻尼器一体化圆柱滚子轴承保持架振动特性的影响

当轴承径向载荷为4 000 N,弹性环凸台个数为8个,弹性环凸台宽度为5 mm,凸台高度为0.4 mm,转速从5 500～13 500 r/min变化时,对圆柱滚子轴承的保持架振动特性进行分析。

图5和图6分别为不同转速工况下圆柱滚子轴承和含ERSFD结构的圆柱滚子轴承保持架振动加速度幅频特性;图7为不同轴承转速工况下圆柱滚子轴承和含ERSFD结构的圆柱滚子轴承保持架振动加速度级图;图8为不同转速工况下圆柱滚子轴承和含ERSFD结构的圆柱滚子轴承保持架打滑率特性图。图9为不同转速工况下圆柱滚子轴承和含ERSFD结构的圆柱滚子轴承保持架质心轨迹图。

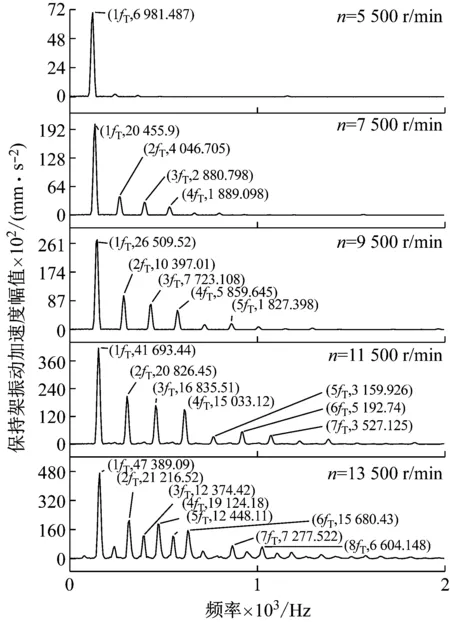
图5 不同转速下非ERSFD轴承保持架的振动频谱图

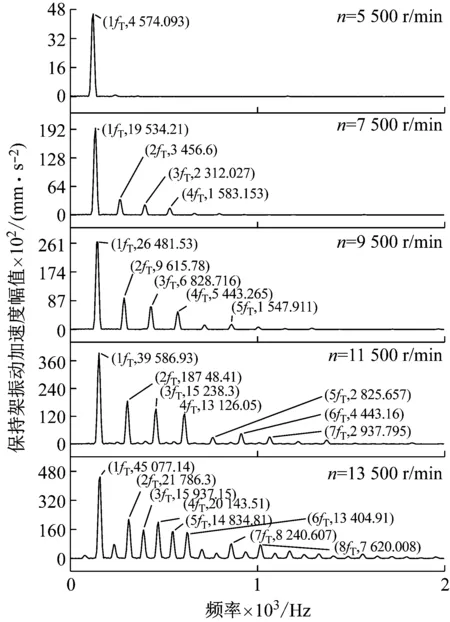
图6 不同转速下ERSFD轴承保持架的振动频谱图

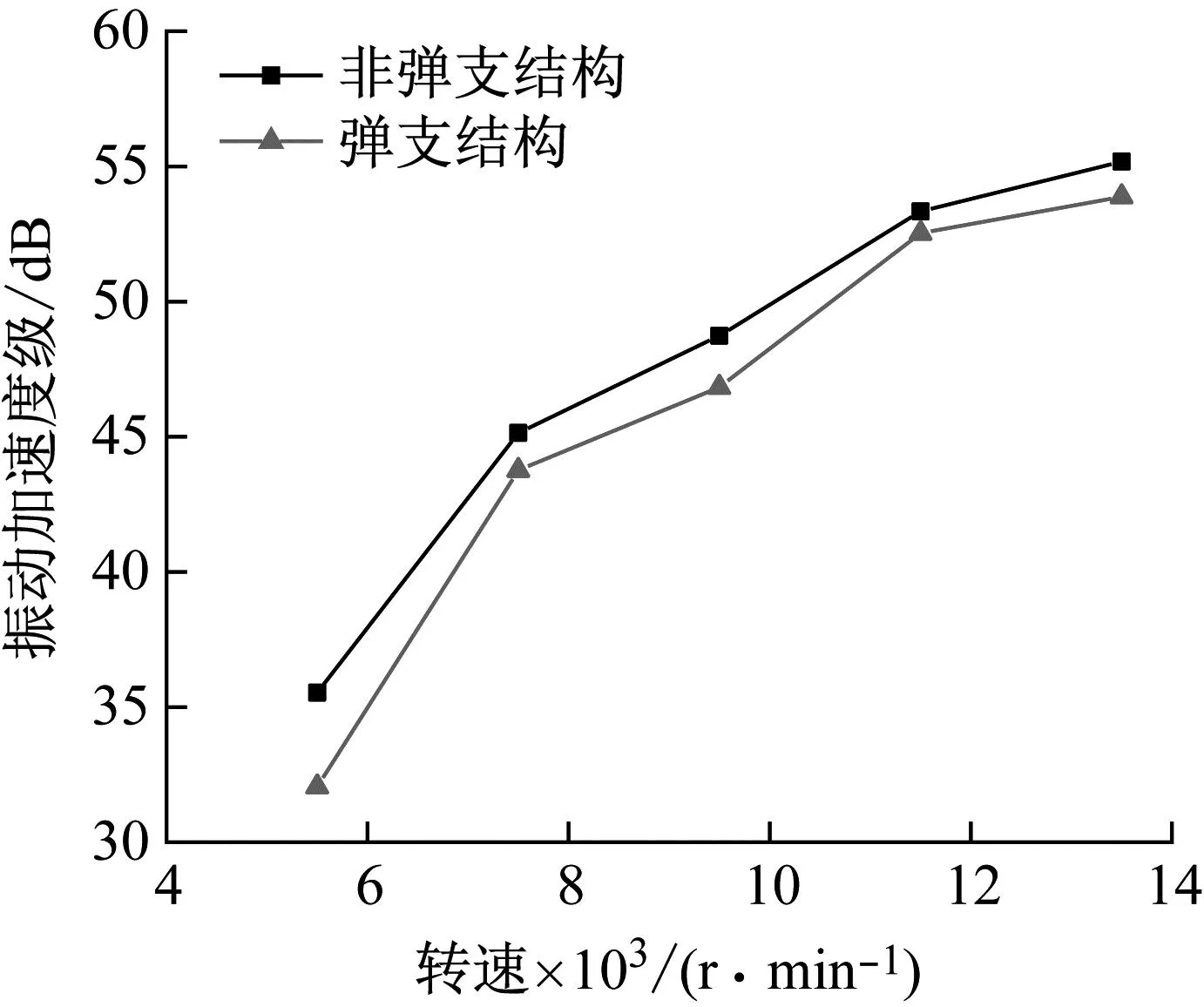
图7 轴承转速对保持架振动加速度级的影响

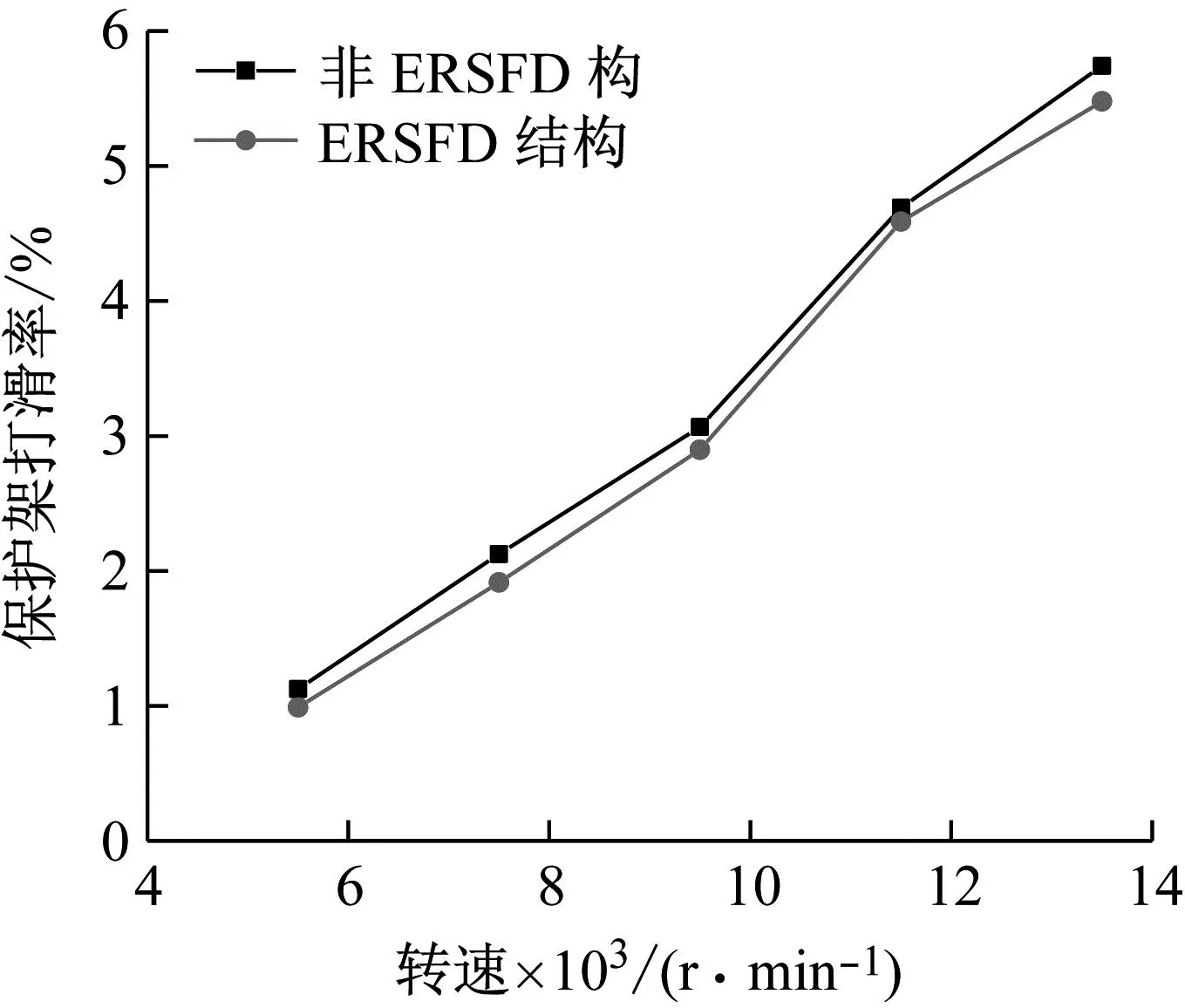
图8 轴承转速对保持架打滑率的影响

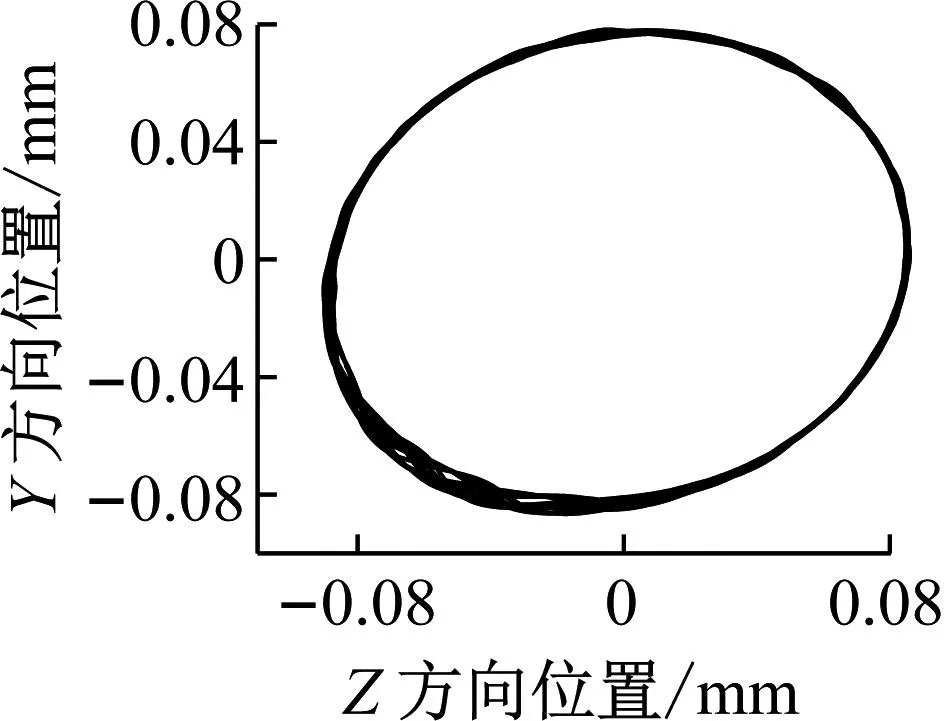
(a) 5 500 r/min未装配ERSFD

由图5和图6可知,保持架加速度Y方向上fT(fT为保持架涡动频率)的谐波次数和其对应的幅值都随转速的增加而增加。由图7可知,相同转速工况下含ERSFD结构的圆柱滚子轴承比圆柱滚子轴承振动加速度级小2.4%～9.8%。由图8可知,保持架打滑率随着转速的增加而增加;圆柱滚子轴承与含ERSFD结构的圆柱滚子轴承在相同转速工况下相比保持架打滑率增加4.7%～12.2%。由图9可知,随着轴承转速的增加,保持架质心轨迹逐渐由椭圆涡动变得混乱,在11 500 r/min时开始变得无序;装配ERSFD的圆柱滚子轴承保持架质心轨迹在相同工况下比未装配ERSFD的规律。

图5～9表现出的现象是因为随着轴承转速的增加,滚子受到的离心力增大,使得滚子外抛加剧,与内滚道间拖动力减小,保持架受到径向作用增大,使滚子与保持架之间的冲击频率增加,振动幅值增大,保持架打滑率也随之增加,保持架质心轨迹变得混乱。ERSFD油膜力产生的油膜阻尼减小了轴承的进动半径,并衰减轴承整体振动,使保持架运动更为稳定,因此在相同工况下含ERSFD结构的轴承保持架更为稳定。

2.2 径向载荷对弹性环式挤压油膜阻尼器一体化圆柱滚子轴承保持架振动特性的影响

当轴承转速为11 500 r/min,弹性环凸台个数为8个,弹性环凸台宽度为5 mm,凸台高度为0.4 mm,径向载荷从4 000～120 000 N变化时,对圆柱滚子轴承的保持架振动特性进行分析。

图10和图11分别为不同径向载荷下圆柱滚子轴承和含ERSFD结构的圆柱滚子轴承保持架振动加速度幅频变换图;图12为不同径向载荷下圆柱滚子轴承和含ERSFD结构的圆柱滚子轴承保持架振动加速度级图;图13为不同径向载荷下圆柱滚子轴承和含ERSFD结构的圆柱滚子轴承保持架打滑率特性图。图14为不同径向载荷下圆柱滚子轴承和含ERSFD结构的圆柱滚子轴承保持架质心轨迹图。

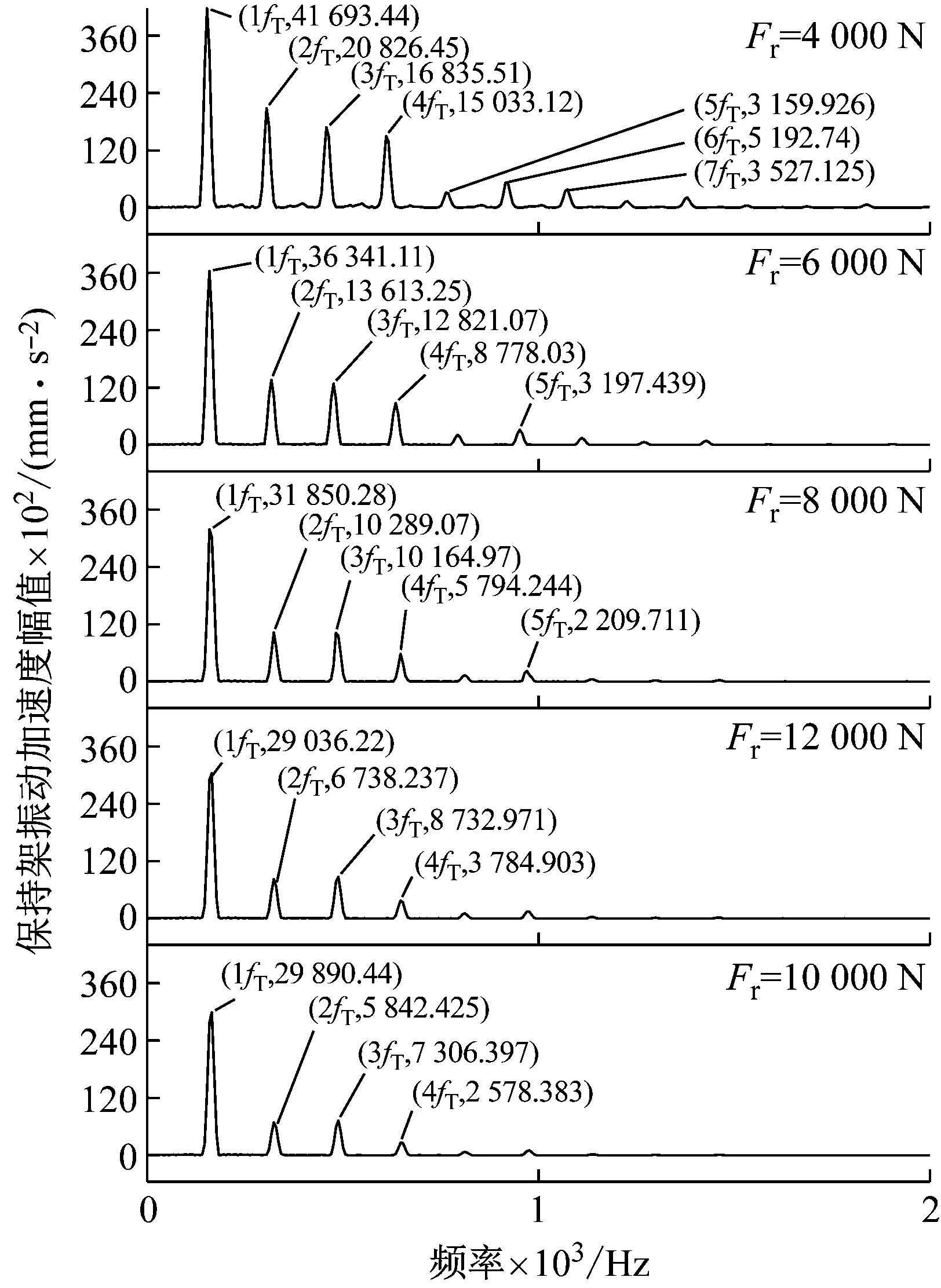
图10 不同径向载荷下非ERSFD轴承保持架的振动频谱图

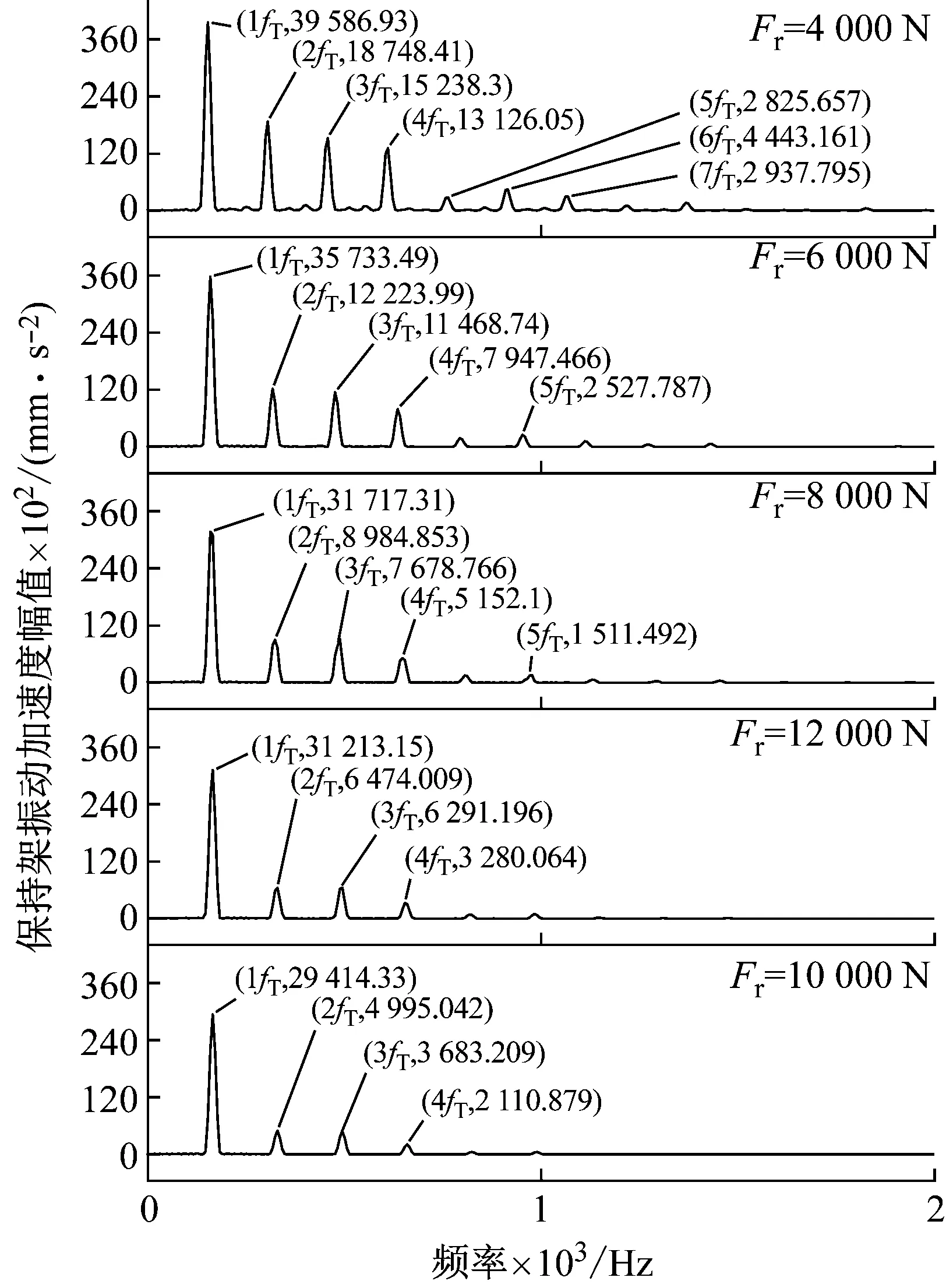
图11 不同径向载荷下ERSFD轴承保持架的振动频谱图

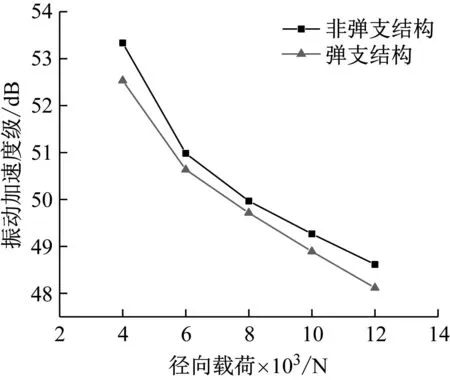
图12 不同径向载荷对保持架振动加速度级的影响

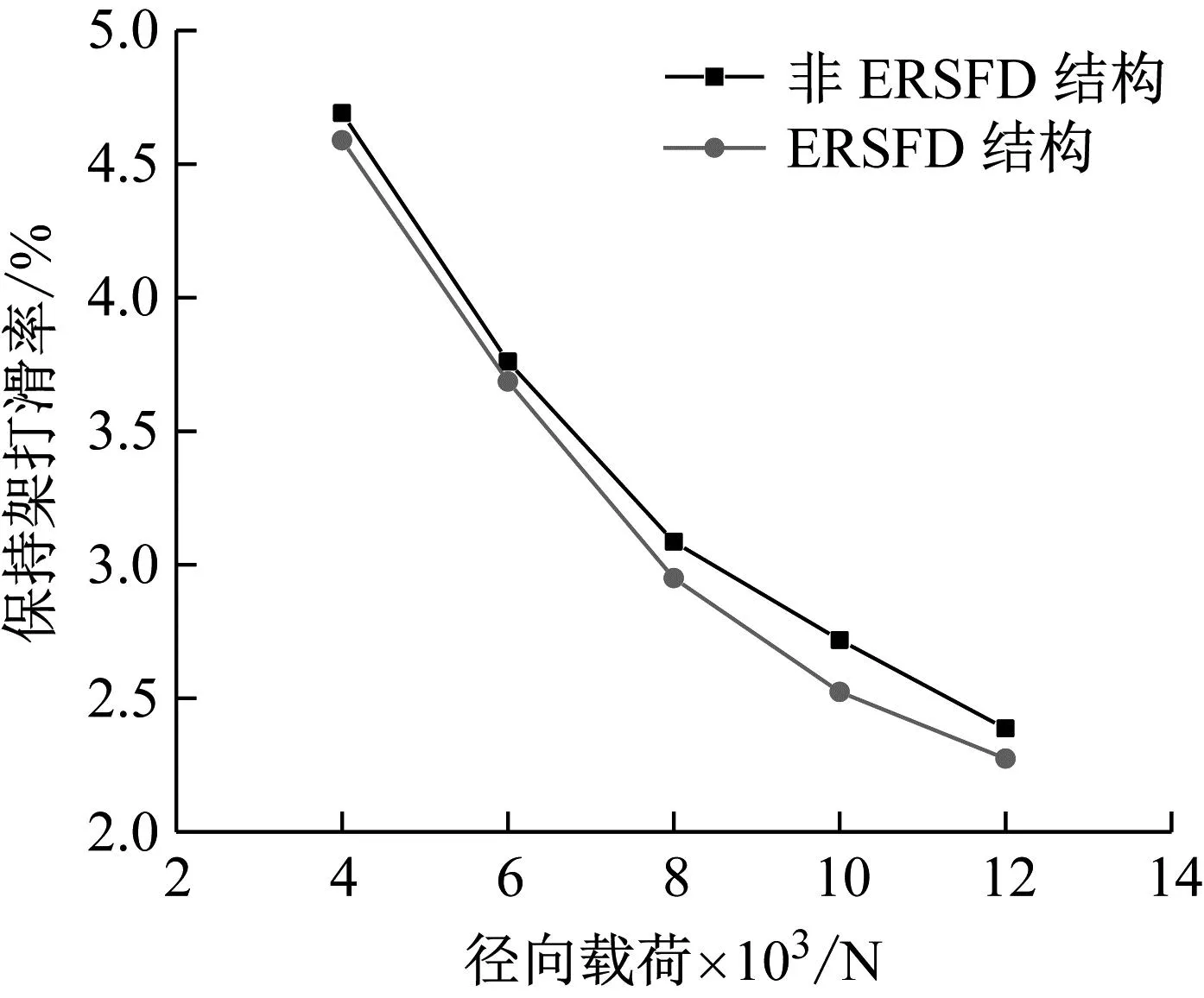
图13 径向载荷对保持架打滑率的影响

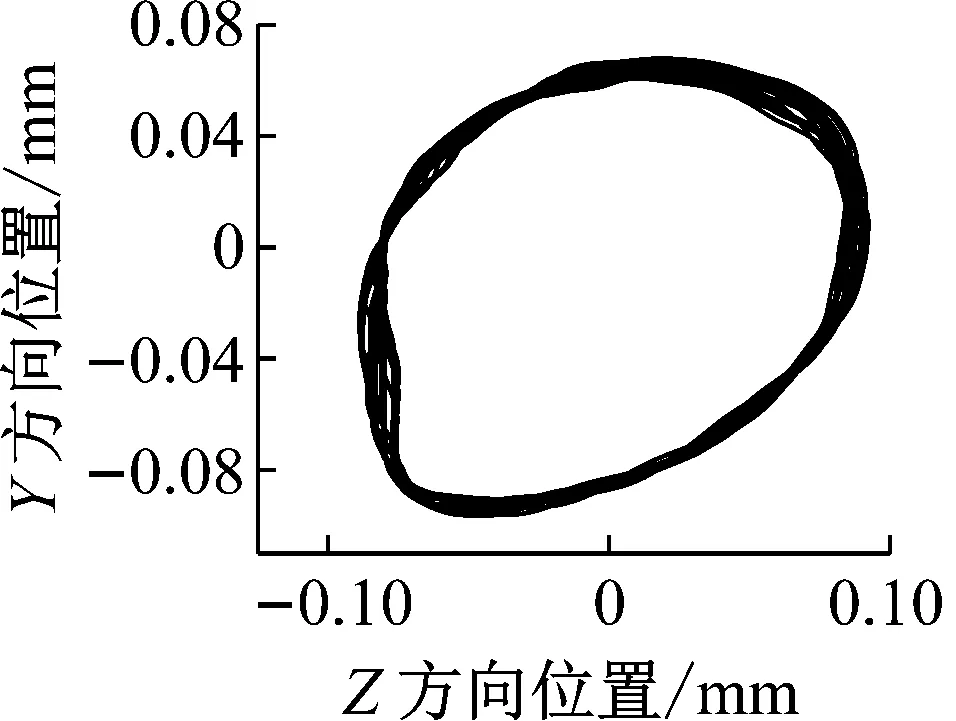
(a) 4 000 N未装配ERSFD

由图10和图11可知,保持架Y方向上的fT的谐波次数和其对应的振动加速度幅值都随着径向载荷的增加而减小。由图12可知,相同径向载荷下含ERSFD结构的圆柱滚子轴承比圆柱滚子轴承振动加速度级小1.32%～1.89%。由图13和图14可知,保持架打滑率随着轴承所受径向载荷的增加而减小;圆柱滚子轴承与含ERSFD结构轴承在所受相同径向载荷下相比保持架打滑率增加4.4%～7.9%,保持架打滑率更为混乱。

图10～12表现的现象是因为随着轴承受到径向载荷的增加,轴承承载区滚子的数量增加,滚子对保持架的拖动增加,滚子与保持架兜孔间的摩擦力增大,因此保持架的振动减小。图13和14表现的现象是因为随着轴承所受径向载荷的增加,滚子与滚道间的接触载荷随之增加,使得滚子的运动受到限制,造成保持架打滑率随着径向载荷的增加而降低。ERSFD结构产生的油膜阻尼使轴承运行更为稳定,所以在相同工况下含ERSFD结构的轴承保持架运行更为稳定,打滑率降低。

2.3 弹性环凸台数量对弹性环式挤压油膜阻尼器一体化圆柱滚子轴承保持架振动特性的影响

当轴承转速为11 500 r/min,所受径向载荷为4 000 N,弹性环凸台宽度为5 mm,凸台高度为0.4 mm,弹性环凸台个数从8～16个变化时,对圆柱滚子轴承的保持架振动特性进行分析。

图15为不同弹性环凸台个数时轴承保持架振动加速度幅频特性;图16为不同弹性环凸台个数时保持架振动加速度级图;图17为不同弹性环凸台个数时轴承保持架打滑率特性图。图18为不同弹性环凸台个数时保持架质心轨迹图。

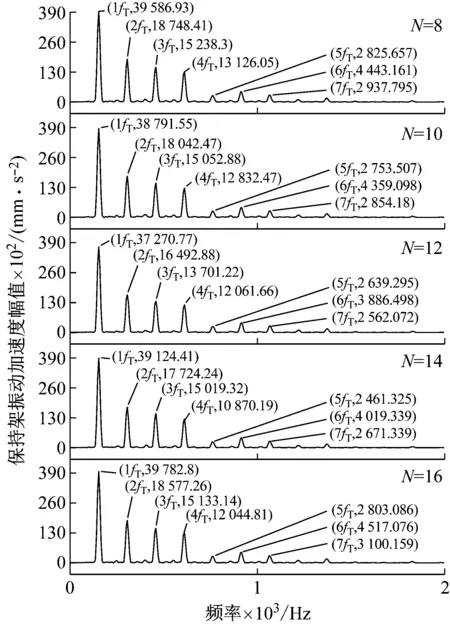
图15 不同凸台个数下轴承保持架的振动频谱图

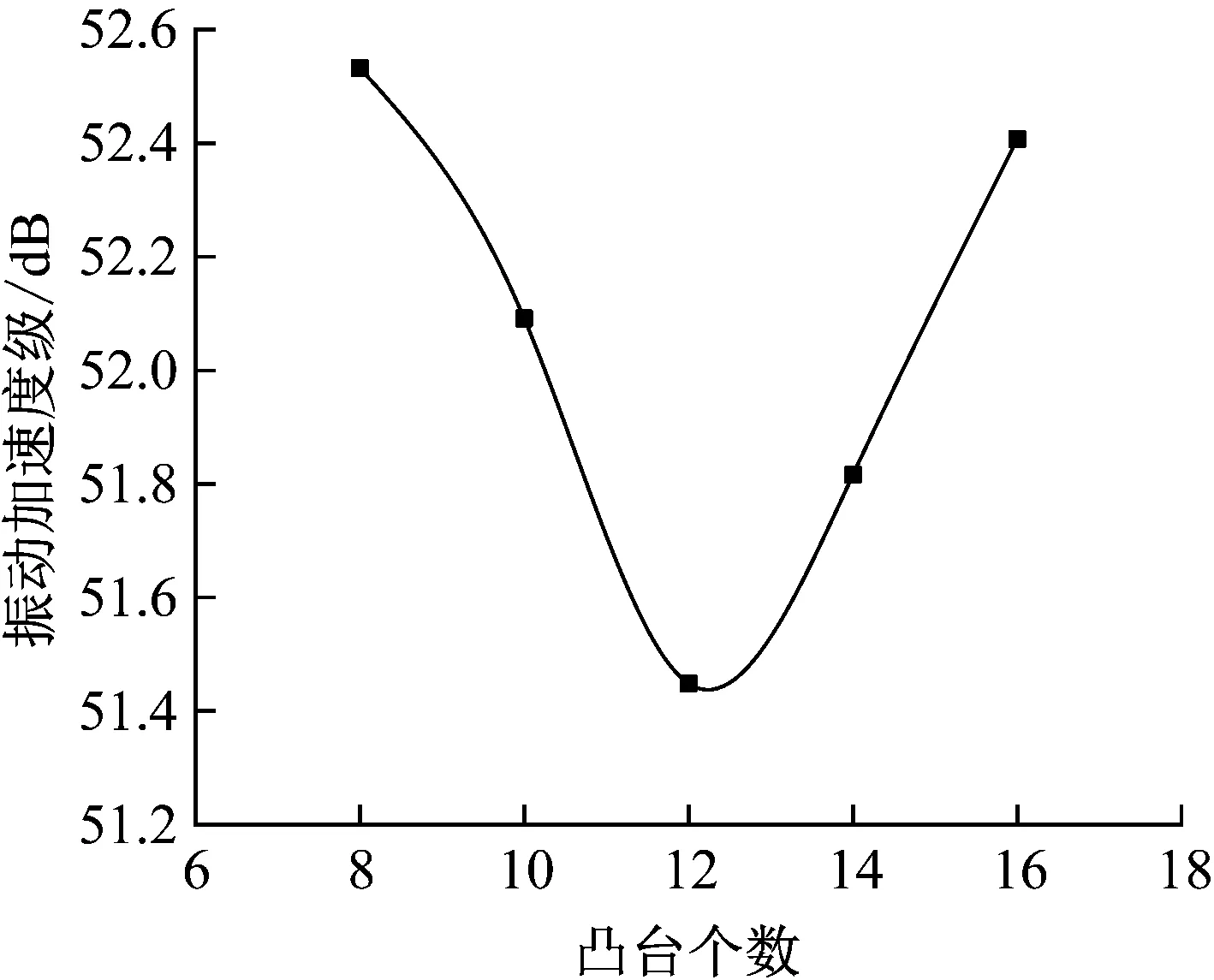
图16 凸台个数对保持架振动加速度级的影响

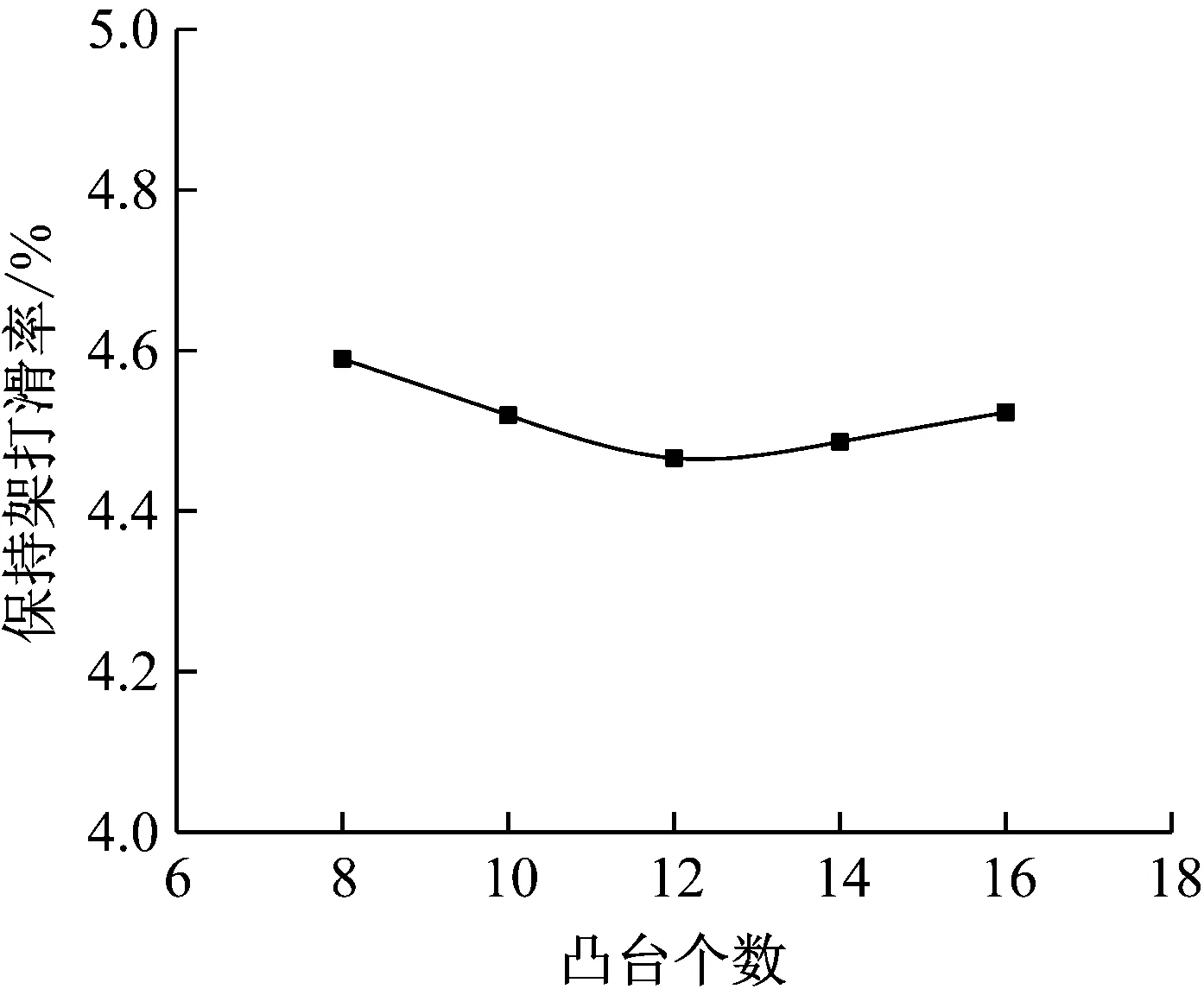
图17 凸台个数对保持架打滑率的影响

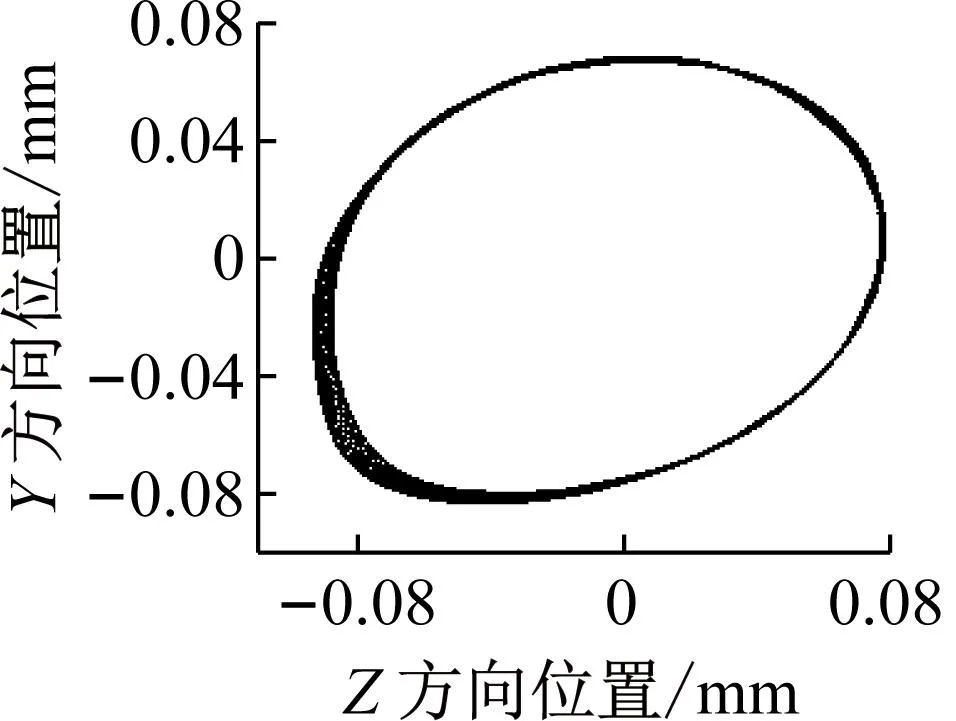
(a) 凸台个数8

由图15和图16可知,可知,保持架Y方向上各fT对应的振动加速度幅值和振动加速度级随着弹性环凸台个数的增加先降低后升高,在凸台个数为12个时最低。由图17和18可知,保持架打滑率和质心轨迹随着凸台个数的增加影响较小,与振动加速度幅值和振动加速度级规律相同。

图15和图16表现的现象是因为随着凸台个数的增加,弹性环的刚度随之增加,在凸台个数为12时ERSFD与轴承耦合下的阻尼作效果最佳;随着刚度的继续增加,弹性环与轴颈可视为刚性接触,ERSFD阻尼效果降低;但凸台数越少,弹性环刚度越小,这样会导致弹性环支承刚度在周向上分布不均匀,容易引起振动的非线性问题,所以保持架的振动幅值及加振动速度级在此参数以及工况下随着弹性环凸台个数的增加先减小后增加。图17和图18表现的现象是因为保持架运动随着振动加速度幅值和振动加速度级的减小而变得相对稳定,使得保持架与滚子间运动稳定,所以保持架打滑率减小。

2.4 弹性环凸台宽度对弹性环式挤压油膜阻尼器一体化圆柱滚子轴承保持架振动特性的影响

当轴承转速为11 500 r/min,所受径向载荷为4 000 N,弹性环凸台个数为8,凸台高度为0.4 mm,弹性环凸台宽度从5～13 mm变化时,对圆柱滚子轴承的保持架振动特性进行分析。

图19为不同弹性环凸台宽度时轴承保持架振动加速度幅频特性;图20为不同弹性环凸台宽度时保持架振动加速度级图;图21为不同弹性环凸台宽度时轴承保持架打滑率特性图。图22为不同弹性环凸台宽度对保持架质心轨迹的影响。

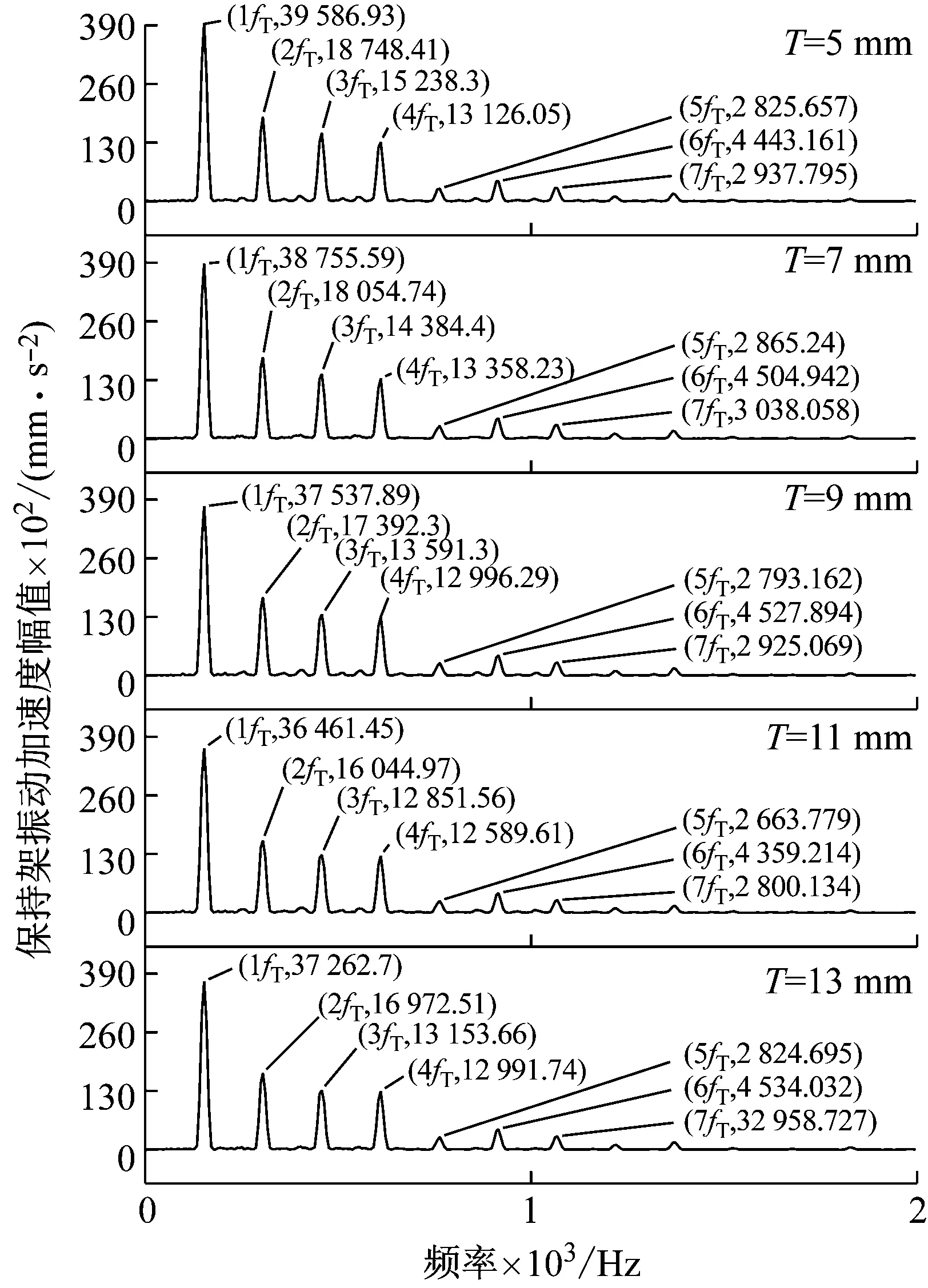
图19 不同凸台宽度下轴承保持架的振动频谱图

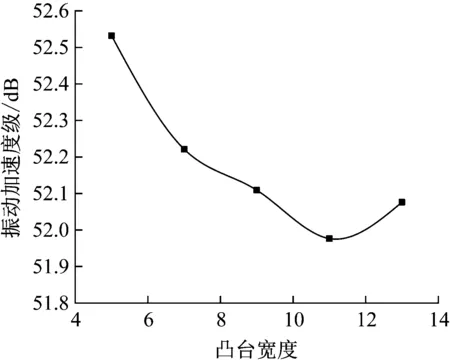
图20 凸台宽度对保持架振动加速度级的影响

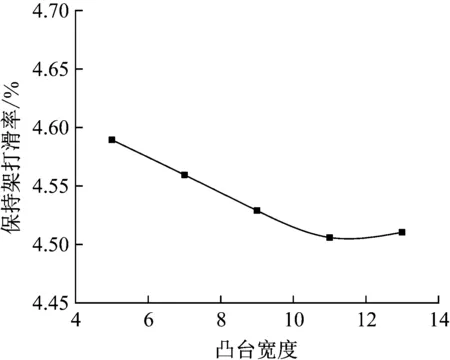
图21 凸台宽度对保持架打滑率的影响

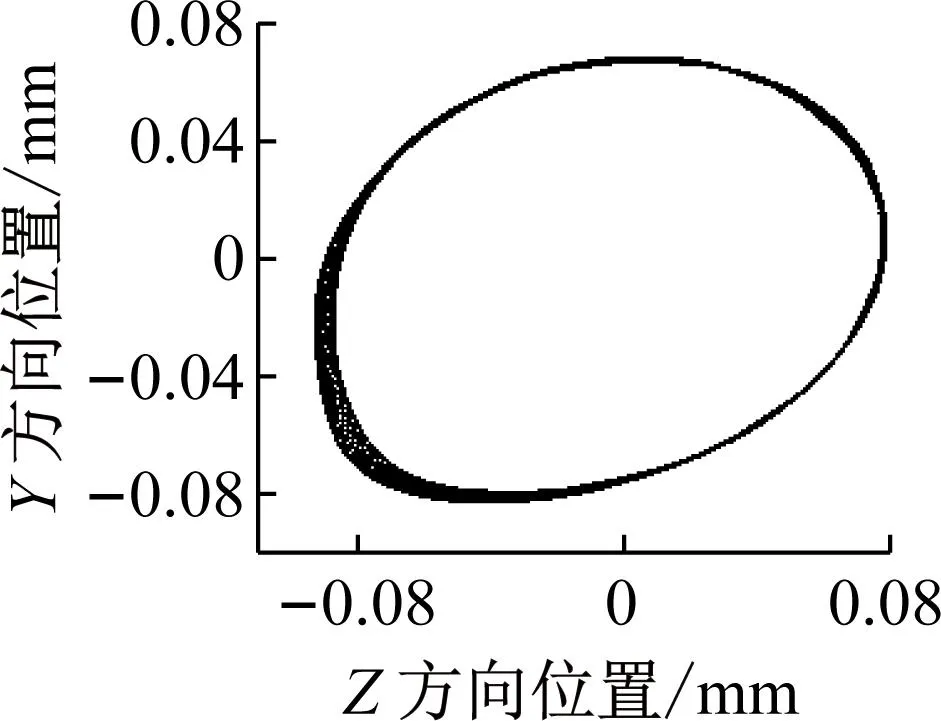
(a) 凸台宽度5 mm

由图19和图20可知,可知,保持架Y方向上各个fT对应的振动加速度幅值和振动加速度级随着弹性环凸台宽度的增加先减小,在凸台宽度13 mm时略微增加,在凸台宽度为11 mm时最低。由图21和22可知,凸台宽度的增加对保持架打滑率的影响较小,与振动加速度幅值和振动加速度级规律相同。

图19、20、21和22表现的现象是因为随着凸台宽度的增加,使得每个凸台间的距离减小,弹性环刚度增加,由此可以看出改变弹性环凸台宽度与凸台个数的规律是几乎等价的。所以保持架振动加速度幅值和振动加速度级随着凸台宽度的增加先减小后增加,保持架打滑率和质心轨迹规律与增加凸台数相同。

3 试验验证

本文采用航空轴承保持架动态性能测试试验台对表1中结构参数的弹性环式挤压油膜阻尼器一体化圆柱滚子轴承保持架打滑率进行试验,验证本文所建立模型和计算结果的准确性。

本文试验采用的弹性环式挤压油膜阻尼器一体化圆柱滚子轴承打滑率测试试验机整体结构如图23所示,试验台如图24所示。试验机主要由试验台、冷却装置、蒸发器、高压气源、设备润滑系统、变频装置、液压加载系统、工控机、数据采集系统和操控台组成。试验机主体由转子系统、传感器和点主轴等结构构成;冷却装置、蒸发器、高压气源和变频装置保证电主轴的正常使用。加载系统主要采用液压加载方式,由基础载荷施加系统、冲击载荷加载系统和压力传感器构成,为系统提供试验载荷;设备润滑系统为系统提供滑油;数据采集系统和工控机用于采集保持架实际转速,并对试验系统进行状态监控。

图23 试验机整体结构

图24 ERSFD一体化轴承试验台

试验时,试验轴承安装在主体底座内,由主体压盖压紧固定。径向加载组件安装在主体压盖上,通过活塞竖直向下对轴承施加载荷;通过比例阀—压力传感器—加载活塞—计算机实现加载的闭环控制;驱动采用高速电主轴,调速系统由智能变频器和电主轴组合构成。高速电主轴在高速下运行平稳,由给定变频器的控制信号使电机运转,实现无级变速,电机实际转速值由转速传感器测量得到并反馈给计算机,计算机对转速的控制量进行PID调节后D/A输出形成系统闭环控制。试验台原理如图25所示。

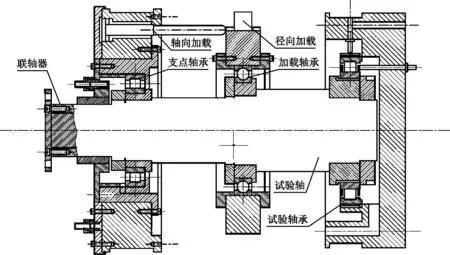
图25 试验台原理图

保持架转速测量的准确性影响保持架打滑率的可靠性。弹性环式挤压油膜阻尼器一体化圆柱滚子轴承保持架实际转速是利用在保持架的被测端面涂覆深色的标记,区分保持架的颜色,当保持架旋转时,红外光传感器将被测量的转速变化转换成光信号的变化,借助光电元件把光强度变化转换成电信号,实现保持架实际转速的测量。保持架转速测试原理如图26所示。

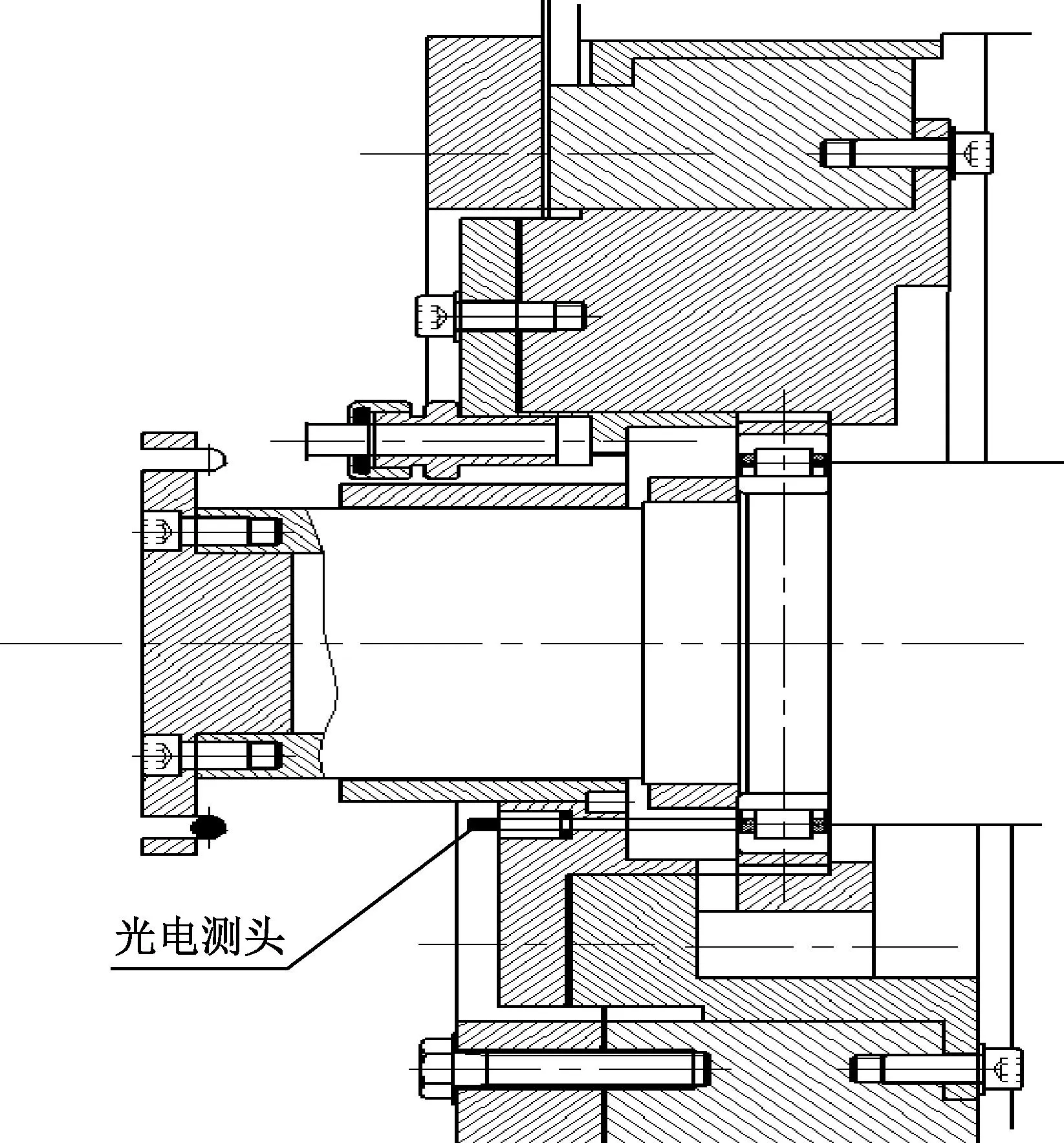
图26 保持架测量安装示意图

选取有无装配弹性环式挤压油膜阻尼器的圆柱滚子轴承保持架打滑率试验过程中典型工况与仿真结果中的保持架打滑率进行对比。图27为轴承转速为8 000 r/min,径向载荷范围在2 000～6 000 N时,有无装配ERSFD的轴承保持架打滑率对比图。图28为轴承径向载荷为4 000 N,转速范围在6 000～10 000 r/min时,有无装配ERSFD的轴承保持架打滑率对比图。

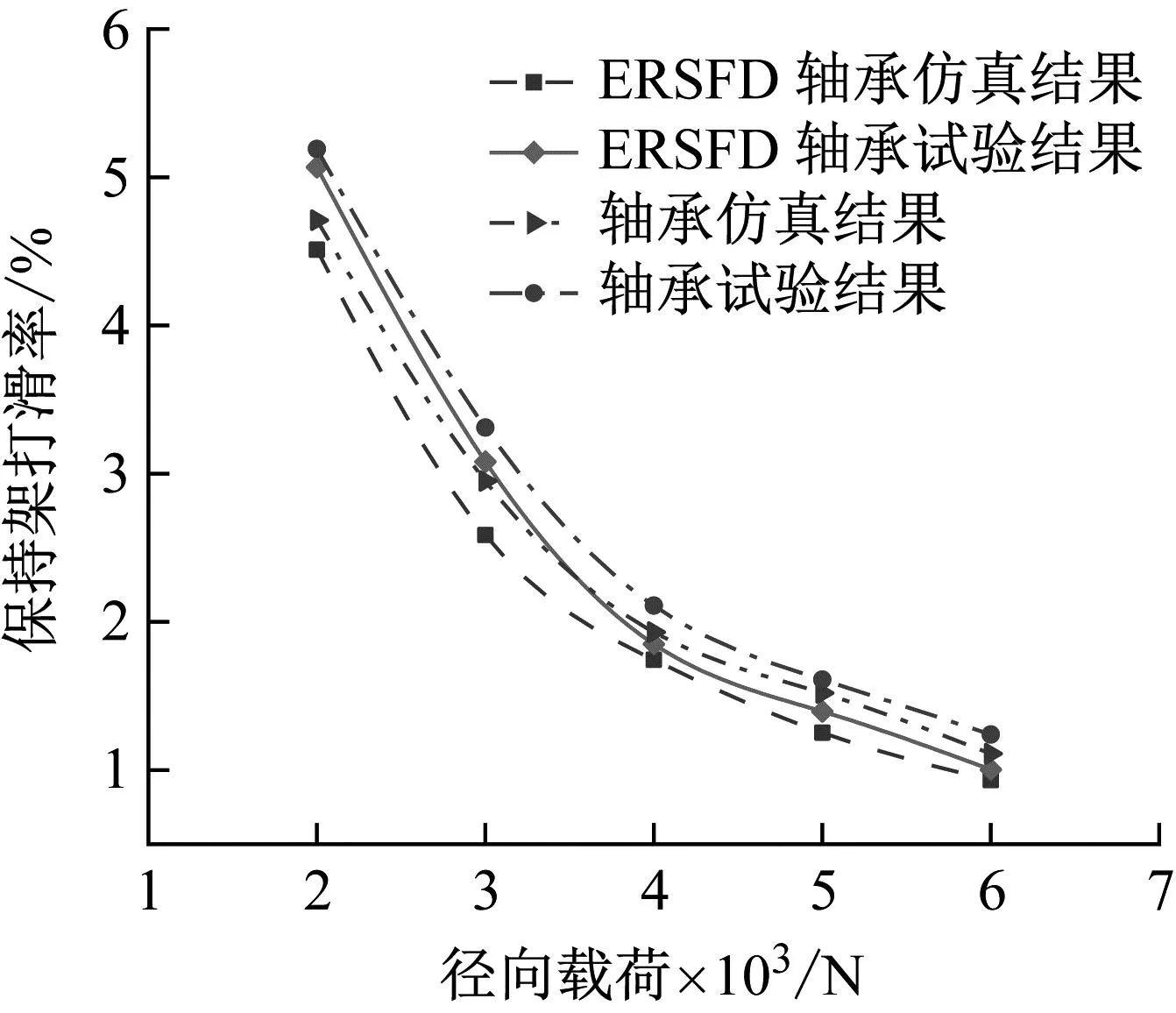
图27 径向载荷对保持架打滑率的影响

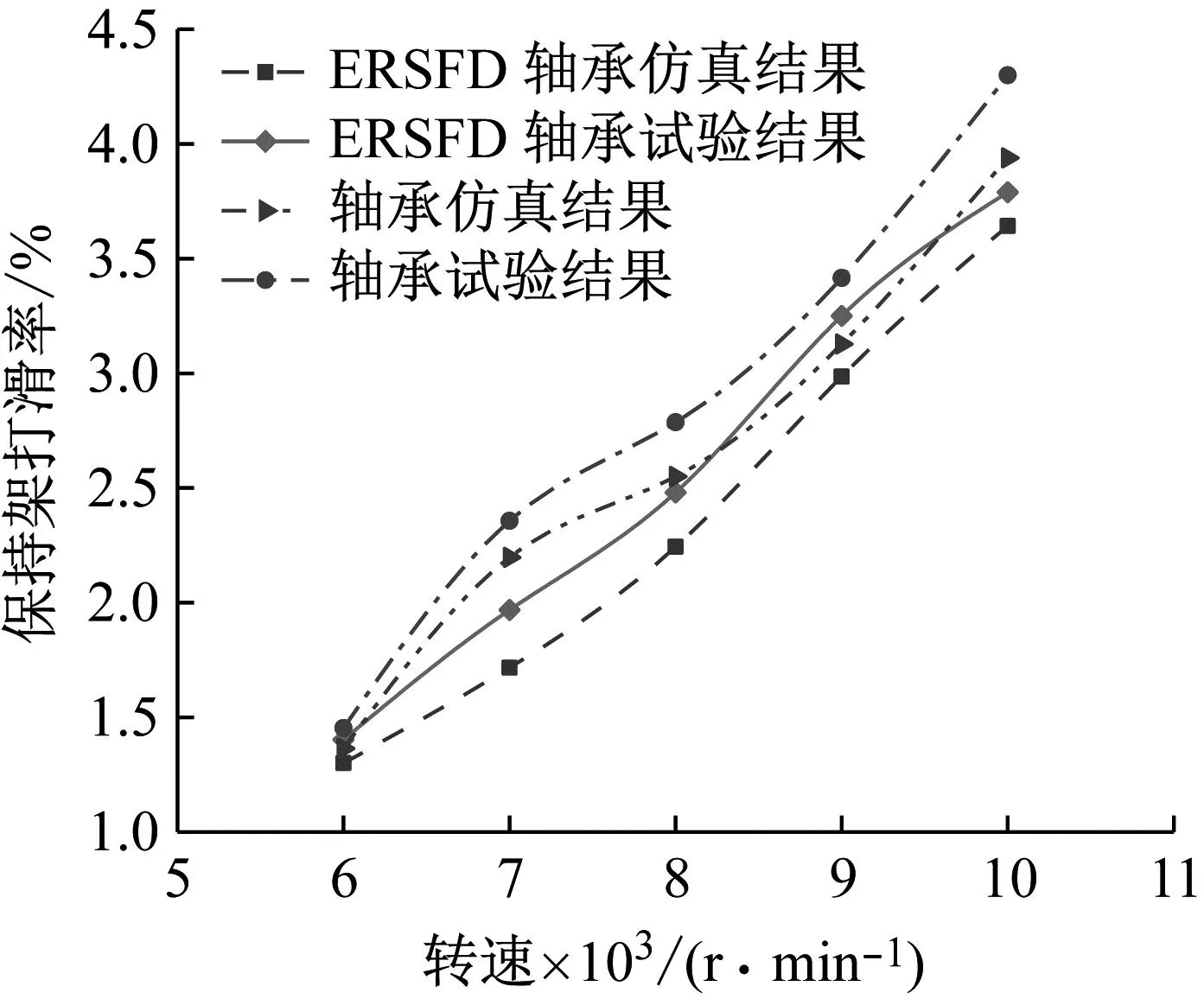
图28 转速对保持架打滑率的影响

由图27和图28对比结果可以看出,仿真结果与试验结果最大误差不超过15%,且装配ERSFD的圆柱滚子轴承打滑率比未装配的轴承保持架打滑率低,一定程度上验证了本模型的正确性。出现误差的原因可能是试验中传感器的测量误差、润滑油含有一定杂质等情况,使轴承保持架打滑率试验结果略高于仿真结果。

4 结 论

考虑弹性环式挤压油膜阻尼器与圆柱滚子轴承的相互耦合,研究了不同工况条件与弹性环结构参数对弹性环式挤压油膜阻尼器一体化圆柱滚子轴承保持架振动和打滑率的影响。结论如下:

(1)与圆柱滚子轴承相比,弹性环式挤压油膜阻尼器一体化圆柱滚子轴承的保持架稳定性提高。带ERSFD的轴承fT所对应的振动幅值比未含ERSFD小,振动加速度级小1.32%～9.8%,保持架打滑率小4.4%～12.2%,运行更稳定。

(2) 工况条件对弹性环式挤压油膜阻尼器一体化圆柱滚子轴承的保持架稳定性影响较大。随着径向载荷的增加,保持架频谱图中fT谐波次数减少,对应的振动幅值降低,振动加速度级降低,保持架打滑率减小;随着轴承转速的增加,保持架频谱图中fT谐波次数增多,对应的保持架振动幅值、振动加速度级都增加,保持架打滑率逐渐增加。

(3) 随着凸台数量和凸台个数的增加,保持架的振动幅值及振动加速度级均随先减小后增大;过大的弹性环刚度相当于弹性环与轴颈刚性连接,ERSFD的阻尼作用降低;过小会导致弹性环支承刚度在周向上分布不均匀,所以要选择合适的弹性环结构参数。在此模型中最优参数为:凸台个数12个、凸台宽度5 mm组合时。