复合磨床砂轮架模态分析与试验研究

陈俊生,姚振强,汤振荣

(上海交通大学 机械与动力工程学院,上海 200240)

高精度数控转台是实现精密磨削的关键所在,是惯导测试仪器、超精加工、检测计量以及微机电系统以及纳米器件制造中不可缺少的设备[1],构成了数控机床的核心回转类功能部件,为数控机床提供分度旋转或?联动旋转运动,与机床的直线轴和其他旋转轴配合实现复杂零件的多自由度联动加工,满足不同类型零件的加工要求[2]。

砂轮架转塔结构的动态性能是评价磨床自激振动和受迫振动的重要指标,不但与加工精度相关,而且对机床可靠性与精度保持性有很大影响。国内外许多学者对转台动态性能进行了分析,张会杰等[3]分析了负载变化对机床刚度的影响。王成禹等[4]研究了不同静压轴承刚度对凸轮轴磨床砂轮架模态的影响。胡育佳等[5]运用贝叶斯理论和运行模态分析结合的方法识别了砂轮架的模态。范晋伟等[6]分析了影响数控凸轮磨床砂轮架模态的因素,并对其进行了优化。Zheng等[7]基于自功率谱分析了砂轮架的模态参数。Xu等[8]研究了砂轮架位置和丝杠轴承结合面刚度对砂轮架动态性能的影响规律。方兵等[9]利用拉格朗日力学原理计算轴承结合部刚度和阻尼,建立机床回转轴有限元分析模型,并进行试验验证了模型的可靠性。

赫兹接触理论自1881年提出后,广泛用于弹性体接触建模。郑溢[10]基于赫兹理论建立了主轴箱角接触轴承有限元分析模型,并对刚度进行修正,用试验验证了模型的通用性。王一鸣[11]对磨床砂轮修整器的滚珠导轨进行动态性能分析,利用赫兹接触理论计算了结合部5自由度刚度。米良等[12]基于赫兹接触理论分析了高速主轴轴承的刚度,建立综合考虑主轴转速和轴承预紧力的动静态特性模型。李朕均等[13]基于赫兹接触理论结合热网络的方法,建立滚珠丝杠系统角接触轴承动态热力耦合分析模型,可以预测轴承非线性工况下的接触特性。

目前对于高精度砂轮架动态性能的研究集中于动态参数的识别与设计优化,而对砂轮架整体进行动力学建模的研究很少。本文基于赫兹接触理论计算了角接触轴承结合部刚度,采用弹簧阻尼单元替代轴承滚子,其中上角接触轴承弹簧阻尼单元沿滚珠接触角分布,下转台轴承依据出厂刚度数据,沿径向和两侧轴向设立弹簧阻尼单元,建立了B轴砂轮架转塔滚动结合部有限元分析模型。对砂轮架整体进行模态分析,得到前六阶振型和固有频率。开展了模态试验验证了模型的可靠性,对砂轮工作转频提出建议,为减少磨削颤振、提高磨削精度的优化方向提供参考。

1 砂轮架转塔结构

精密磨床的砂轮架转塔主要包括驱动机构、分度测量机构、锁紧机构和支撑机构等机构。图1所示为上海机床厂有限公司研发的某一大型内外圆磨床B轴砂轮架转塔,主要包括端面电主轴、外圆电主轴、内圆电主轴、上座、中座、下座等结构。上座和中座构成了转塔主体,中座用螺纹固定三个电主轴,实现了工件一次装夹可以完成对内圆、外圆、端面的磨削工序。

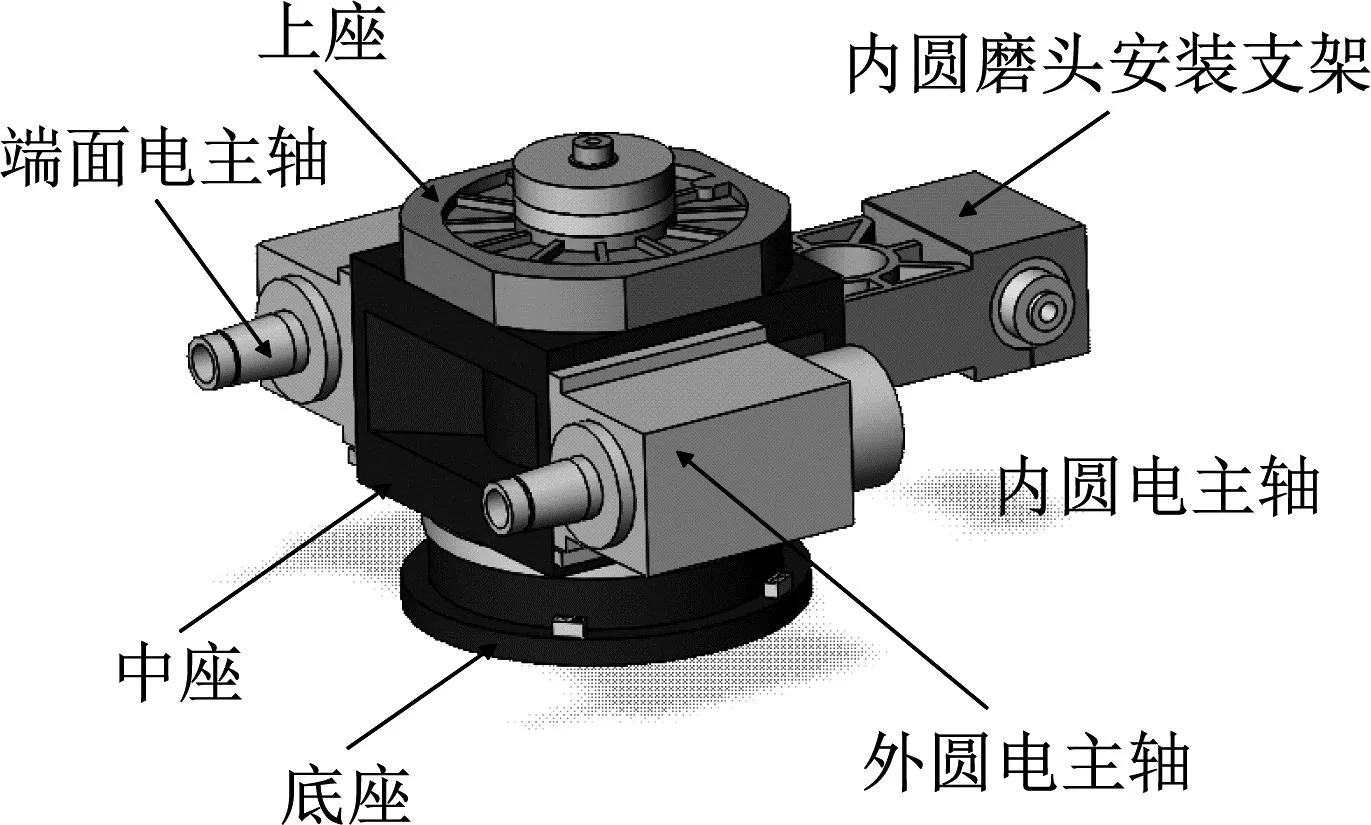
图1 B轴砂轮架转塔简化模型

2 建立有限元分析模型

B轴砂轮架转塔结构复杂,结合部参数设置是有限元分析的难点。转塔结构结合部主要包括螺栓固定结合部和轴承滚动结合部。对于轴承滚动结合部,需要将滚子和内外圆的接触部分进行网格细化,才能比较精确地模拟滚动结合部刚度和阻尼。以赫兹接触理论计算为准,经过计算,局部网格尺寸需要小于接触半宽长度,误差才能达到5%以内,这无疑大大加重了计算,且存在不收敛的可能性。为简化滚动轴承接触界面,以赫兹接触理论为指导计算轴承刚度,在有限元中以弹簧阻尼单元代替。

B轴转塔底座与中座采用转台轴承连接,型号为YRT260。转台轴承在轴向分布两排止推滚子,径向分布一排径向滚子,可以承受双向轴向载荷和径向载荷,同时还拥有较大的倾覆刚度。上座与中座通过螺纹连接构成回转体。上座与主轴用一副角接触轴承连接,内圈用紧固螺母固定在主轴,外圈用轴承盖压紧,从而实现角接触轴承的轴向预紧,型号为7216AC。B轴砂轮架转塔轴承结构如图2所示。

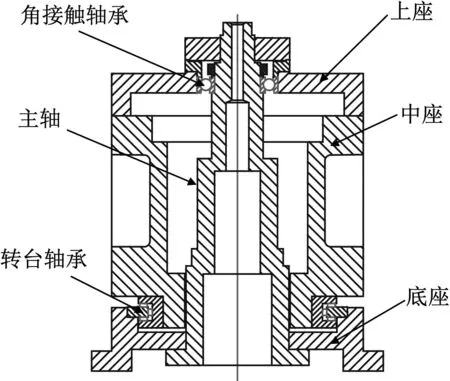
图2 砂轮架转塔轴承结构

2.1 角接触轴承滚珠刚度计算

精密主轴轴承在正常工作下需要预加一定轴向载荷,目的是提高轴向旋转精度、减小支承的轴向和径向窜动量、提高轴承刚度。根据赫兹接触理论,当接触面尺寸远小于两接触物体时,可以将接触简化为弹性接触。分析轴承内外圈和滚子的变形和尺寸关系,可以认为滚子与内外圈的接触为赫兹接触。

如图3所示,钢球与内外圈接触后,弹性趋近量δ和接触力Q的关系为[14]

(1)

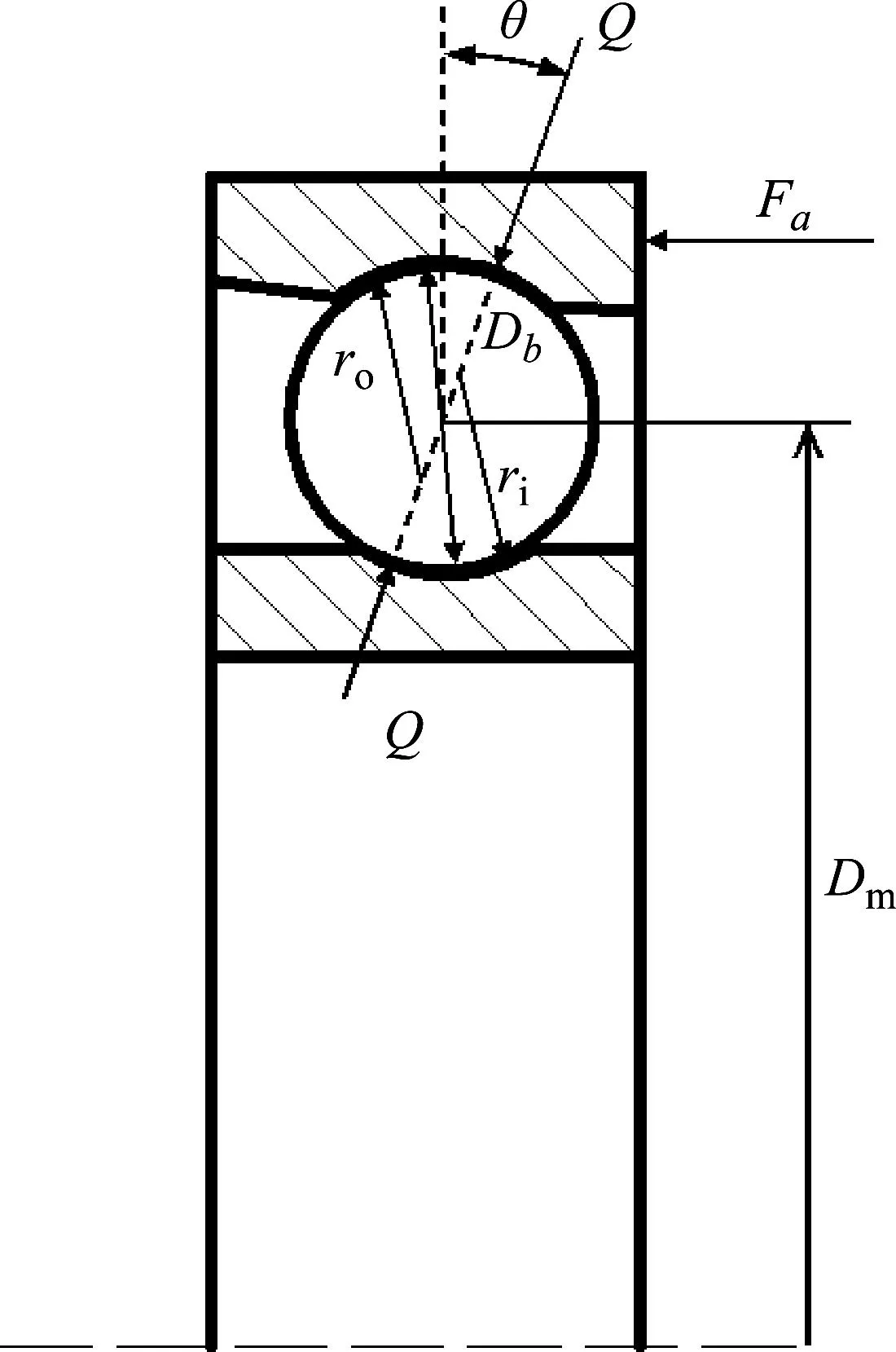
图3 角接触轴承受力分析

式中,K为载荷变形系数。其表达式为

(2)

(3)

式中:k为与接触面形状相关的参数;L和F为第一类和第二类完全椭圆积分;∑ρ为钢球与内外圈接触曲率和,E为钢球等效弹性模量。

在低速转动或静止时,钢球与内外圈滚道承载后沿接触力方向的总弹性变形δn可以表示为

δn=δi+δo

(4)

再代入式(1)中可以得到

(5)

得到总载荷系数Kn为

(6)

根据式(1),求Q对δn的导数,可以得到法向刚度表达式为

(7)

再依据轴承结构几何关系,可以得到轴向载荷Fa和法向刚度K的关系

(8)

2.2 有限元建模

依据实际工况,角接触轴承选择预紧力为2 000 N,对应法向刚度为352.24 N/μm;轴承包含滚珠16个,接触角为25°,沿轴承环向设置16个弹簧阻尼单元,方向和滚珠接触法向相同,如图4所示。YRT260转台轴承上下层推力滚子和径向滚子各144个,参考轴承出厂文件,轴向滚子刚度为12 810 N/μm,径向滚子刚度为8 100 N/μm,综合考虑整体结构,将阻尼比定为0.05,以此为参数在有限元模型中设置弹簧阻尼单元,如图5所示。

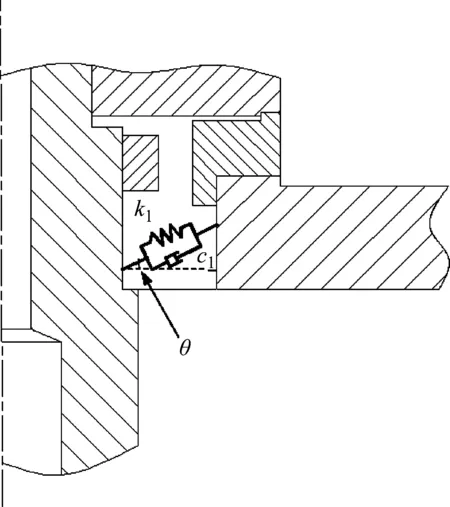
图4 角接触轴承弹簧阻尼等效单元

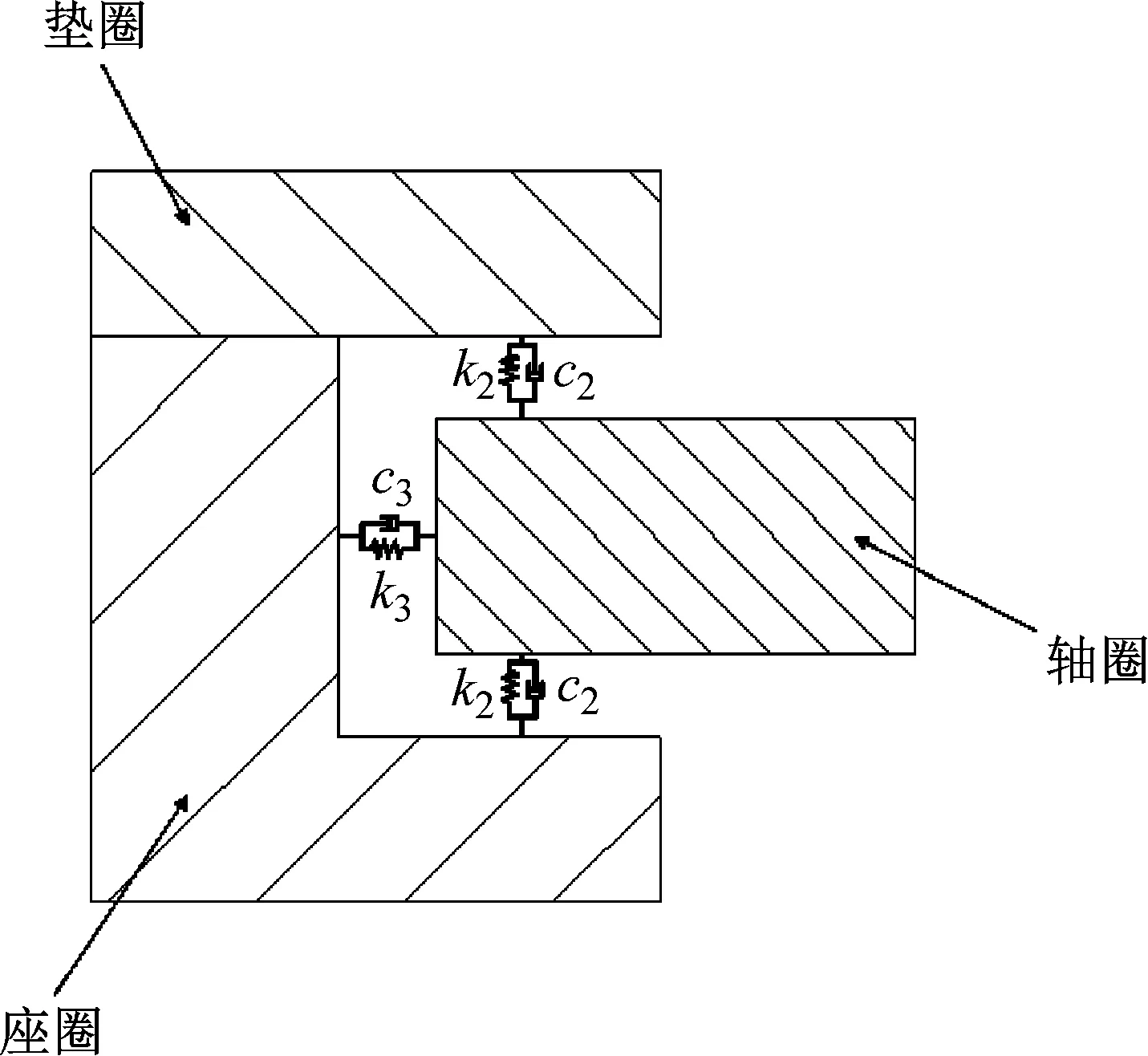
图5 转台轴承等效弹簧阻尼单元

首先用SolidWorks软件进行三维建模。进行模态分析前,需要对结构进行简化,B轴砂轮架外部存在很多细微结构,如倒角、小孔、固定板等,这些细微结构质量占比很小,根据圣维南原理,有限元分析结果基本不受这些小特征影响,因此可以将这些工艺特征去除。导入ABAQUS有限元分析软件进行前处理,主要包括边界条件设置、网格划分、属性设置等步骤。求解器设定为线性摄动-频率,方法采用子空间迭代法。砂轮架转塔底面与滑板固定,求解约束模态时将底座面的自由度全约束。砂轮架转塔结构包含大量的螺栓连接界面,此类固定结合面刚度要远大于轴承滚动结合面,可以近似等效为刚性连接,在有限元分析软件中,螺栓固定结合部设定为绑定约束[15]。网格划分选择六面体。经过网格划分后的节点数为421 010个,单元数251 404个。主要结构材料属性如表1所示。

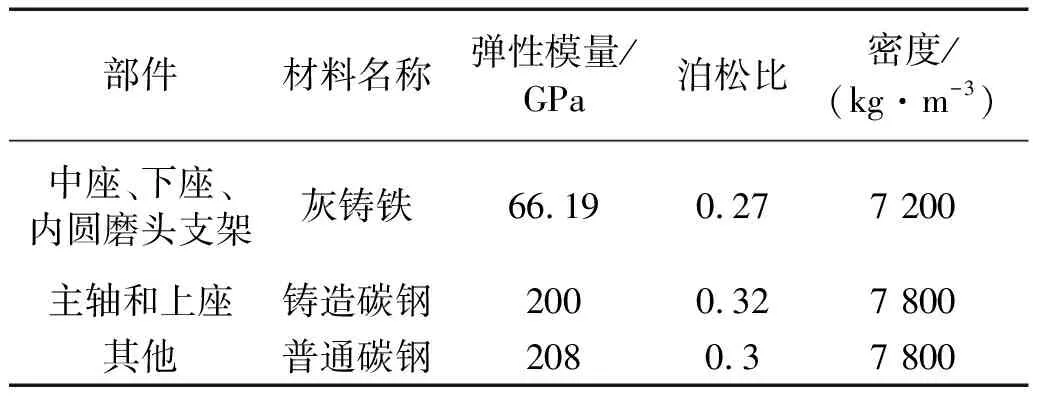
表1 材料属性

3 模态分析

完成有限元模型的前处理后,下一步进行求解。对于多阶自由度的弹性体,理论上具有无穷多阶模态,由于低阶固有频率更容易被激励起来,所以只分析前六阶模态[16]。基于有限元分析步骤,在ABAQUS软件中的求解器设置为频率,采用子空间迭代法,提交作业后进入后处理模块。软件输出ODB格式文件,可以查看位移、应力、应变云图,绘制变形过程。前六阶固有频率如表2所示。

表2 砂轮架转塔前六阶固有频率

图6为6阶振型,1阶振型为主轴带动砂轮架外壳绕Z轴的摆动,2阶振型为主轴和转动部分绕X轴的摆动。由于主轴底部用螺纹固定于底座,构成悬臂梁结构,适量减少主轴长度可以提高低阶固有频率。3阶振型为内圆磨头支架沿Y轴的摆动,上座-中座-电主轴-内圆电主轴支架构成的转动部分以上角接触轴承为中心,绕Z轴摆动,振型和固有频率与转台轴承径向滚子刚度有关;4阶振型为转动体沿Y轴上下振动,振型和频率与两副轴承的轴向刚度有关。此两阶振型为结构整体的振动,轴承的径向刚度和轴向刚度对此两阶镇定和固有频率有很大影响,提高固有频率可采用刚度更高、出厂游隙更小的轴承。5阶振型为内圆电主轴支架绕Y轴的摆动;6阶振型为支架与中座连接部分沿Y轴的弯曲变形。其振型和固有频率与支架结构和材料相关,优化支架结构可提高固有频率,减小振动幅值。

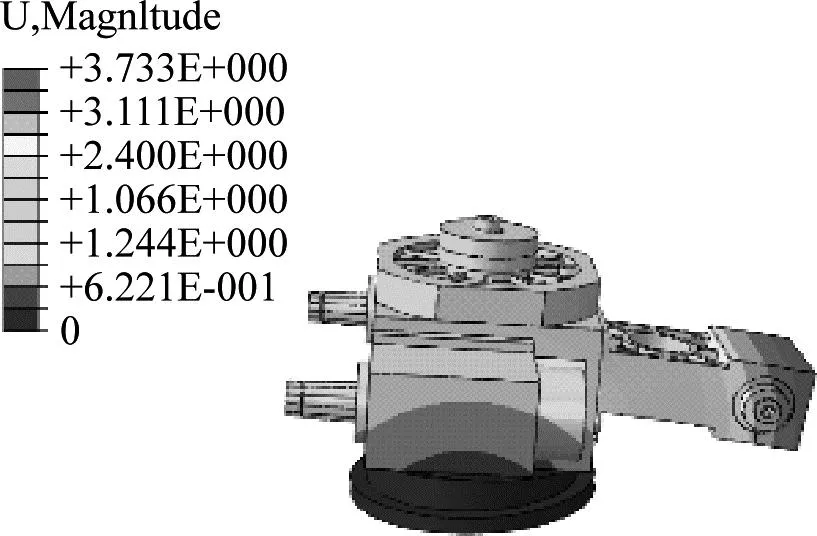
1阶振型

4 动态性能测试

4.1 模态试验

为描述B轴砂轮架转塔整体形态,模态测试前需要根据外形建立框架结构。LMS Testlab提供了点、线、面三种建模方式,如图7所示。根据砂轮架外形结构共布置76个测点,将相邻测量点连接并构建平面,激振点取在外圆电主轴一侧的中座面上,与测量点重合,外形框图如图8所示。测试试验平台为西门子LMS模态测试系统,包括力锤、振动传感器、信号放大器、信号采集器和信号处理系统。试验采用力锤单点敲击,多点拾振的方法。在线框节点上放置三向加速度传感器,记录线框点加速度数值,后利用LMS Testlab分析软件选择固有频率,并将振型可视化。

图7 LMS Testlab软件界面

图8 砂轮架转塔敲击节点与框架

4.2 试验结果

可以得到砂轮架转塔6阶测试模态,表3为仿真频率和试验频率的对比,可以看出6阶固有频率误差均在10%以内。

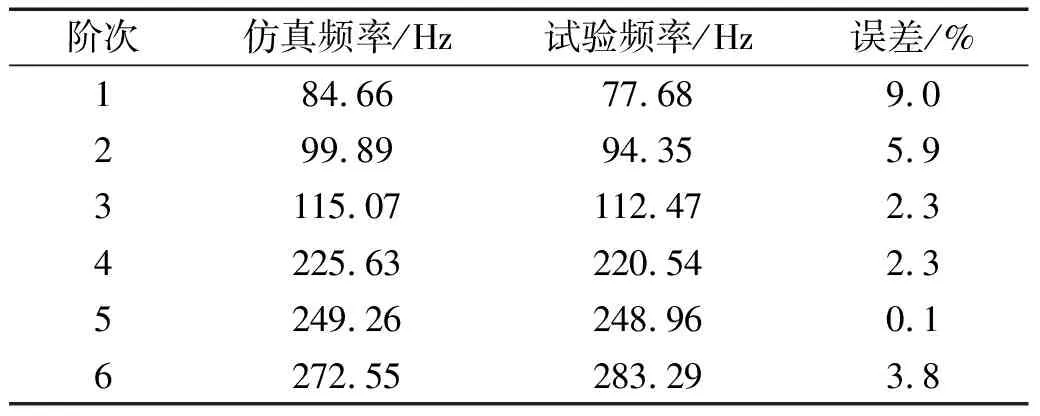
表3 仿真频率和试验频率对比

图9为6阶试验振型,各阶振型与仿真结果相近,验证了有限元模态分析模型的可靠性。对砂轮架转塔结构进行有限元与试验模态分析可知:系统的前6阶固有频率范围在70～300 Hz,应避免外加负载激振频率与固有频率相近。从振型来看振动幅值较大的结构有主轴、上座、中座和内圆电主轴支架;影响低阶振型的因素在于主轴,提高主轴刚度可以增大低阶固有频率,减小振动幅度;轴承刚度影响整个箱体结构的振型和频率;内圆电主轴与中座连接构成悬臂梁结构,其振动幅值、频率与结构和材料相关。由于螺钉固定结合部接触刚度要远大于轴承滚子与内外圈的接触刚度,模态分析中用弹簧阻尼单元替代轴承滚子可以减少有限元建模的难度,较为准确地对固有频率和振型进行预估。

1阶振型

5 结 论

本文以复合磨床砂轮架转塔为研究对象,建立了ABAQUS有限元分析模型,研究其动态性能。采用单点激振、多点拾振的方式开展模态测试试验。得到以下结论:

(1) 依据赫兹接触理论计算了轴承滚珠与内外圈刚度,用弹簧阻尼单元替代轴承结合部,建立可靠的有限元分析模型,简化了建模流程,提高了计算的收敛性。

(2) 根据有限元计算得到的砂轮架转塔前6阶模态,发现固有频率集中在70～300 Hz,可以为砂轮工作转频提供参考。主要的振型为箱体结构和内圆电主轴支架的振动,为整体结构优化提供方向。

(3) 对砂轮架转塔结构开展模态测试,得到6阶试验模态。通过模态试验发现,有限元计算与试验测量振型相近,固有频率误差不超过10%,验证了有限元建模的可靠性,为后续研究提供理论依据。