考虑滞回效应的螺栓连接组合结构非线性随机振动分析

吴鹏辉,王纪磊,毛晨洋,赵 岩,2

(1.大连理工大学 运载工程与力学学部 工业装备结构分析优化与CAE软件全国重点实验室,辽宁 大连 116023;2.大连理工大学 宁波研究院,浙江 宁波 315016)

螺栓连接广泛存在于各种复杂和大型的工业装备中,通过为部件之间传递载荷和能量,对结构的可靠运行起到了重要保障。已有的研究表明,螺栓连接对结构整体动力学行为有显著的影响,而其准确的建模和振动响应分析对于结构设计、性能评估与运维管理具有重要的意义[1]。

对于螺栓连接结构,很多学者在理论、数值及实验方面做了丰富的研究工作[2-4]。Brake对螺栓连接研究的发展方向进行了分析,特别指出由于螺栓界面所存在的复杂摩擦机理还没有得到很好的认识、利用有限元等数值方法进行动力学预测需要高昂的计算成本,发展界面连接复杂结构有效的计算方法仍是一项重要的课题。现有的螺栓连接建模工作可分为基于宏观实验的唯象模型和考虑结合界面微观接触机理的物理模型[5]。唯象模型主要有Jenkins模型、Iwan模型、Bouc-Wen模型等。Tamatam等[6]利用Jenkins模型进行接触建模,研究了磨损对航空发动机叶盘动力学性能的影响。康佳豪等[7]基于Iwan模型描述了连接界面微滑移和宏观滑移行为,利用多谐波平衡法和时频变换求解了摩擦振子的稳态响应。王东等[8]提出了一种动力学降阶方法,并基于Iwan模型开展了相关的动力响应分析。在考虑微观接触机理的物理模型方面,Balaji等[9]基于粗糙接触理论提出了一种多尺度接触本构模型,建立了粗糙度参数局部变化与局部接触力、能量耗散之间的关系。Li等[10]提出了一种多尺度接触建模方法来计算切向接触刚度并再现了螺栓连接界面的摩擦滞回现象。在连接结构动力学分析中,最通用的是时域直接积分法,其显著优势是可以处理不同激励和不同非线性的动力学问题,但计算资源消耗、累计误差不可忽略[11];而对于周期激励,谐波平衡法(harmonic balance method,HBM)得到了很好的发展[12]。

上述富有成效的工作大部分基于确定性激励开展,然而很多情况下结构处于随机载荷环境,如海浪、地震、喷气噪声等。对于线性随机振动分析,虚拟激励法[13]可以将结构的平稳随机振动计算转化为简谐振动计算,在获得与传统随机振动CQC(complete quadratic combination)同样精度的分析结果同时计算效率获得显著提升。受限于非线性随机振动分析方法的发展,目前针对多自由度螺栓连接随机振动开展的研究工作还相对较少,且基于频域开展的研究更少。对于非线性随机振动分析,主流求解方法可分为两类:一类是FPK(Fokker-Planck-Kolmogorov)方法[14],但是FPK方程解析和数值求解的应用范围较为严格,很难用于螺栓连接组合结构这类复杂模型;另一类是从确定性非线性振动理论推广的方法,如统计线性化法[15],随机模拟方法[16]等,其中应用广泛的是基于矩等效的统计线性化方法,但是该方法在响应功率谱密度预测上会给出不恰当的结果[17]。

基于上述研究现状,针对考虑滞回效应的螺栓连接组合结构随机振动问题,本文将随机激励利用复指数级数进行展开,结合线性结构随机振动分析的虚拟激励法和多谐波平衡的思想提出了扩展虚拟激励法(extended pseudo excitation method,E-PEM),将非线性随机振动响应功率谱分析的转换为虚拟响应的向量运算。通过引入时频变换(alternating time-frequency,AFT)处理非线性本构在频域计算困难,并针对传统牛顿法处理非连续、非光滑本构时可能出现的收敛性问题,将非线性代数方程的求解问题转换为优化问题,并利用信赖域方法进行求解。数值算例中,以二自由度模型和组合梁模型为研究对象,利用所建立的方法研究了结构非线性随机振动响应功率谱特性。

1 考虑滞回非线性的螺栓连接组合结构动力学方程

对于螺栓连接中的非线性力学行为,学者们提出了多种的非线性模型来描述。根据建模所需数据的不同,螺栓连接建模可以分为:基于状态的建模和基于速度的建模。基于状态的建模包括Jenkins模型、Iwan模型和Bouc-Wen模型等,基于速度的建模中最具代表性的则为库仑摩擦模型。在描述螺栓连接的力学行为时,基于状态的建模需要接触位置在之前时刻的运动状态,而基于速度的建模则只需要当前时刻的速度。对于周期性激励,可以利用Iwan模型结合Masing映射准则进行求解,但是随机载荷作用下的结构通常没有传统的稳态响应形式,为了解决这个问题,本文采用被广泛研究的Jenkins模型进行本构建模。如图1所示Jenkins模型对于摩擦力的表述可以归纳为微分形式和离散形式[18]。Jenkins模型的微分形式和离散形式的不同之处在于:微分形式方便用于时域数值积分方法,离散形式更适用于谐波平衡求解。本文提出的方法采用离散形式的Jenkins模型结合时频变换进行频域随机振动分析。为了对本文方法进行对比验证,在蒙特卡罗模拟法(Monte Carlo simulation,MCS)的时域数值积分中选取了微分形式的Jenkins模型。下面将分别介绍这两类模型。

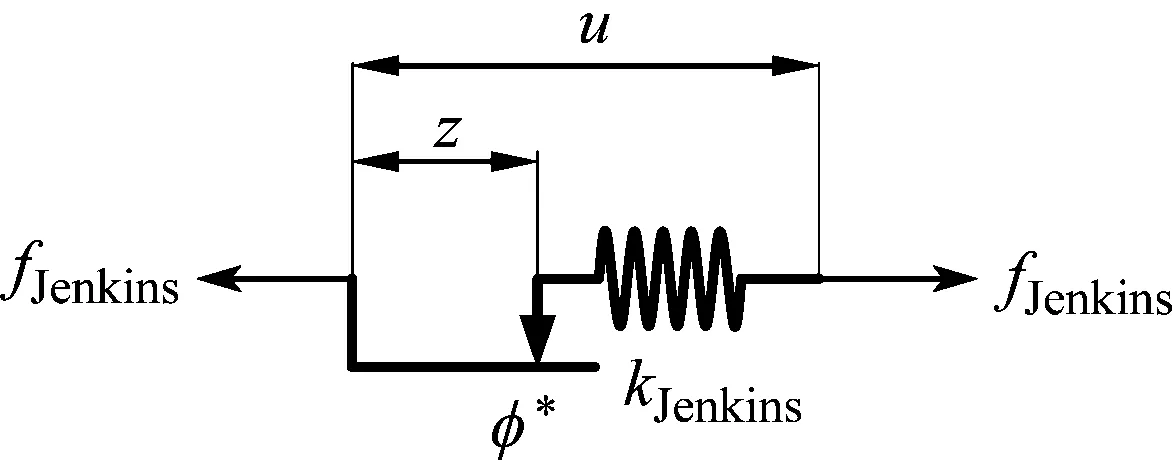
图1 Jenkins模型

1.1 微分形式的Jenkins本构模型

对于摩擦力以微分形式表达的Jenkins模型,其非线性力fJenkins可以表示为

fJenkins=kJenkins(u-z)

(1)

式中:kJenkins为弹簧的刚度,z是滑块元件的位移。其演变规律为

(2)

这里的φ*为临界滑移力

φ*=μFn

(3)

式中:μ为库仑摩擦因数;Fn为接触界面的压力。其对应的滞回曲线如图2所示。

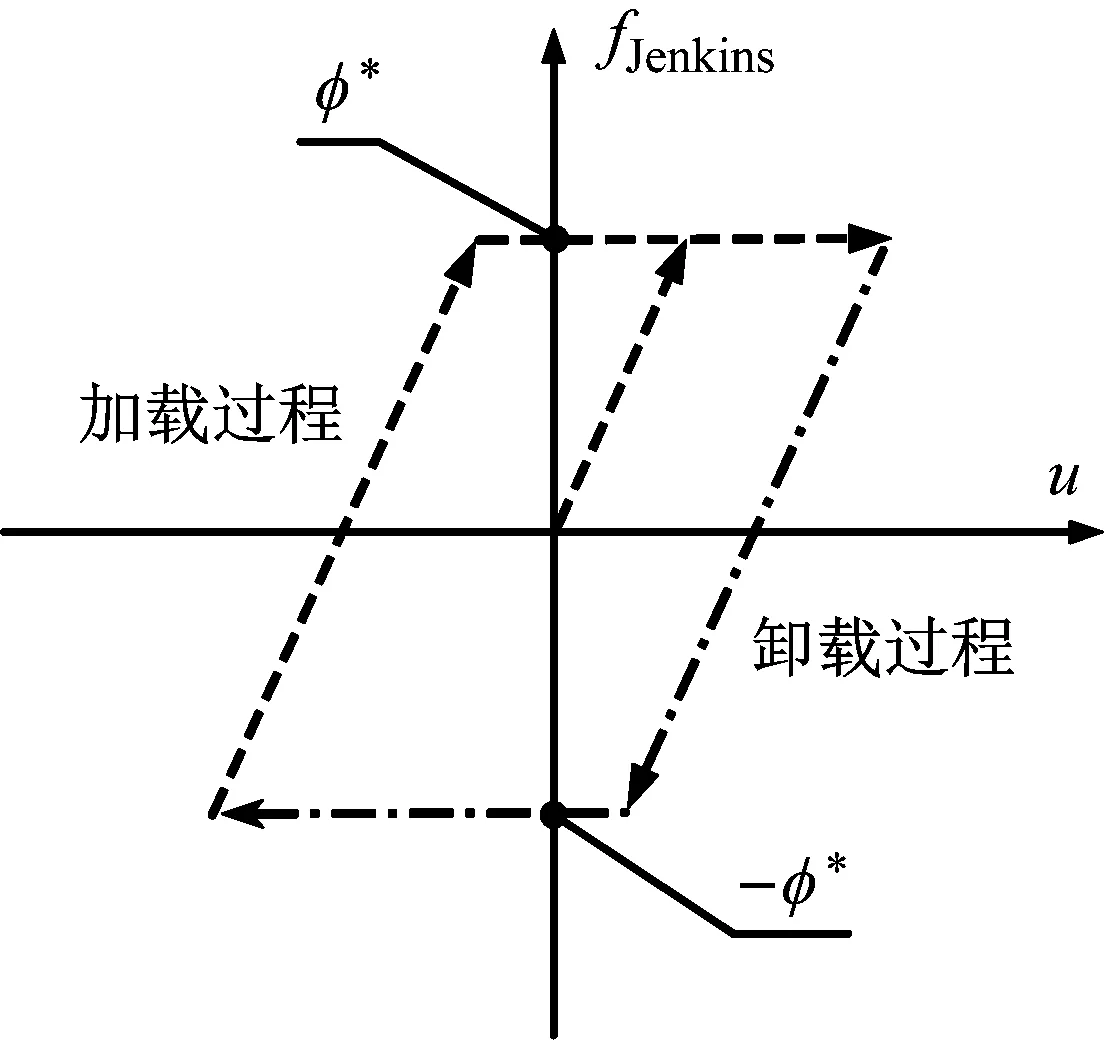
图2 Jenkins模型的滞回曲线

1.2 离散形式的Jenkins模型

基于离散摩擦力形式的Jenkins模型,其非线性力的表达形式为

(4)

相比于微分形式的模型,该模型更适用于谐波平衡法等频域迭代求解方法。利用该临界滑移力φ*,可以判断Jenkins模型的两个状态:滑移和黏滞,当达到临界滑移力时,会出现经典的摩擦行为,否则为纯弹性接触。其中,ftr为第i-1个时间步和第i个时间步之间的临界位置试验力

ftr=fi-1+kJenkins(ui-ui-1)

(5)

1.3 连接组合结构动力学方程

非线性结构的动力学方程可以表达为如下形式

F(t)

(6)

(7)

式中:T为局部到全局的转换矩阵;fJ(fJenkins)为多个Jenkins单元组成的局部非线性力向量。

2 非线性随机振动分析的扩展虚拟激励法

2.1 扩展虚拟激励法

基于三角级数叠加法[19]和欧拉公式,高斯平稳随机过程可以建模为

(8)

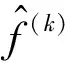
(9)

式中:Sff(ωk)为激励的功率谱密度;Φk为在[0,2π]内均匀分布且相互独立的随机相位角,且满足Φ-k=-Φk。

基于平稳随机激励模拟的相关理论,Roncen等[20]提出了将确定性分析的HBM方法用于随机振动问题。按照类似的思路,下面对非线性结构动力学方程(6)的求解进行多谐波方程推导。假定方程(6)右端的平稳激励向量为F(t)=[f1(t),…,fj(t),…,fn(t)]T,其中第j个自由度的平稳随机激励为fj(t),按照式(8)表达为复指数基底展开的形式

(10)

利用式(10),平稳随机激励向量F(t)表示为

(11)

将式(11)代入多自由度非线性结构的运动方程(6),得到:

(12)

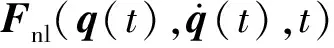
(13)

和

(14)

将式(13)和式(14)代入式(12),则对于频率的各个分量ωk,由多谐波平衡的概念,可以得到如下在频域上描述的非线性代数方程组

(15)

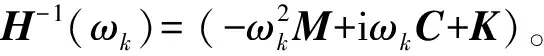
(16)

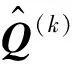
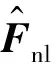
(17)

需要注意FFT虽然可以提高运算速度,但是也对参与运算的样本序列做出了限制,要求样本数为2的幂次方。此外,为了避免信号混叠,并提高所计算非线性力的准确性,通常需要更大的采样频率[22]。为了避免信号泄漏,在FFT的过程中可以对数据进行加窗处理。

在具体实现过程中,对平稳随机过程建立一个特定的时间历程样本,并以此来估计随机过程的统计特征。随机激励样本下的样本响应qi(t),其时域样本历程可以由式(13)给出

(18)

对于随机过程样本qi(t),其频域统计特征用样本功率谱矩阵来表征,定义为

(19)

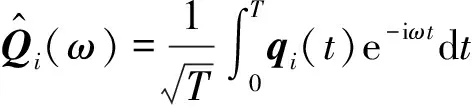
Sqq(ωk)≈E[Sqiqi(ωk)]

(20)

2.2 虚拟响应求解的牛顿法

(21)

其中

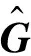
R(Q)=GQ+Fnl-F

(22)

其中:

其中,R[·]代表取实部,I[·]代表取虚部。

牛顿法是求解非线性方程组最有效的方法之一,其迭代计算过程表达为如下

Qp+1=Qp-[∂Rp/∂Q]-1Rp

(23)

式中:上标p代表了迭代次数;[∂Rp/∂Q]是Rp对应的雅可比矩阵。雅可比矩阵[∂Rp/∂Q]可以采用解析方法或有限差分法进行计算。通常解析表达式并不容易得到,这里采用中心差分法计算雅可比矩阵[∂Rp/∂Q]。此外,对于迭代开始,将未考虑结构非线性Fnl的线性解作为初始解。

2.3 牛顿法收敛性问题的讨论

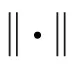
对于Duffing型或多项式型的刚度、阻尼及其混合非线性,由于其对应的非线性本构通常可以表征为连续可导函数,所以雅可比矩阵的计算一般不会存在病态问题,这也保证迭代求解通常是收敛的。但是对于螺栓连接这类的接触非线性模型,其本构函数通常为非光滑、非连续函数,将会导致雅可比矩阵是奇异的,最终导致迭代不收敛。另一方面,如果迭代初始解与真实解的距离较远,牛顿法也可能会不收敛。为了解决传统牛顿法的收敛性问题,研究人员提出了非常多的改进的方法,如弧长延拓、修正牛顿法[23]等。还有一类方法是将非线性方程组的求解问题转换为等价的非线性最小二乘问题,之后利用高斯-牛顿法、Levenberg-Marquardt法、信赖域Levenberg-Marquardt法等求解最小二乘优化问题[24]。对于式(22)中的非线性方程组,可以转化为最小化问题

(24)

3 数值算例

3.1 二自由度模型

选取如图3所示的二自由度模型[26]进行随机振动分析,Jenkins非线性位于两个自由度之间,模型的相关参数均在表1中给出。为了验证本文方法的正确性,采用蒙特卡罗模拟法(MCS)进行对比验证。MCS将式(8)所建立的时域随机激励作用于非线性二自由度模型上,再利用龙格—库塔数值积分方法求解系统响应的时域历程,之后对计算得到的响应时域历程利用功率谱密度估计方法得到样本的功率谱密度,通过对样本功率谱密度进行统计平均,可以得到非线性系统的响应理论功率谱估计。

表1 二自由度模型的参数值

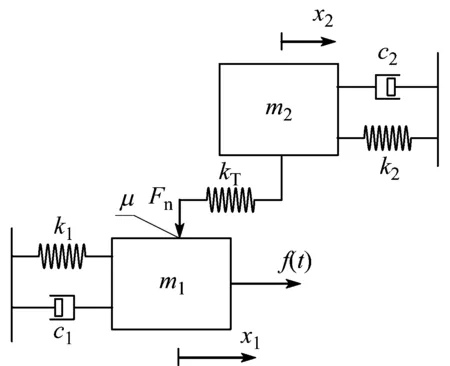
图3 二自由度模型

对于此二自由度模型,激励功率谱Sff(ω)=10 N2/Hz情况下的位移响应样本功率谱密度如图4所示。

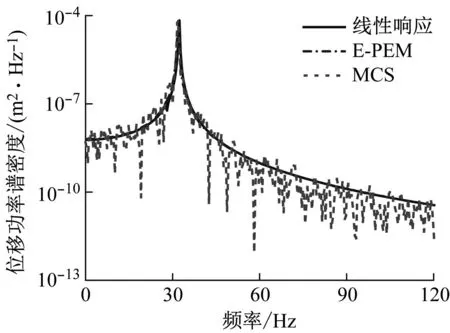
(a) 自由度1

可以看出,E-PEM相比MCS更加光滑,主要是由于MCS在进行非线性响应功率谱估计的过程中存在一定的信号泄漏。从图4可以看出,E-PEM和MCS对于非线性响应功率谱的计算具有较好的一致性。

图5给出了Jenkins非线性在随机激励下的滞回曲线,相比于周期激励作用下滞回曲线,随机激励作用下的滞回曲线与加载历程相关,并不能给出同周期加载一样确定性的滞回曲线。滞回非线性力被限制在了-1～1 N,正好等于库仑摩擦定理的最大滑动摩擦μFn。在虚拟响应求解过程中,将牛顿迭代法、修正牛顿迭代法和信赖域方法进行了对比。图6给出了不同方法下的迭代历程曲线。在相同初始解的前提下,信赖域方法的收敛性最好,表明信赖域方法具有很好的计算优势。虽然牛顿迭代法和修正牛顿法在首次迭代时下降速度很快,但是在雅可比矩阵出现病态后就很难保证结果的收敛性,而信赖域方法通过优化迭代步可以实现全局收敛。

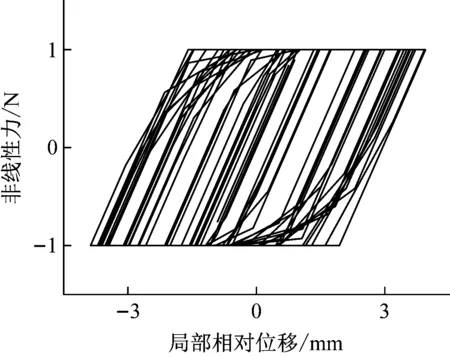
图5 非线性力的滞回曲线

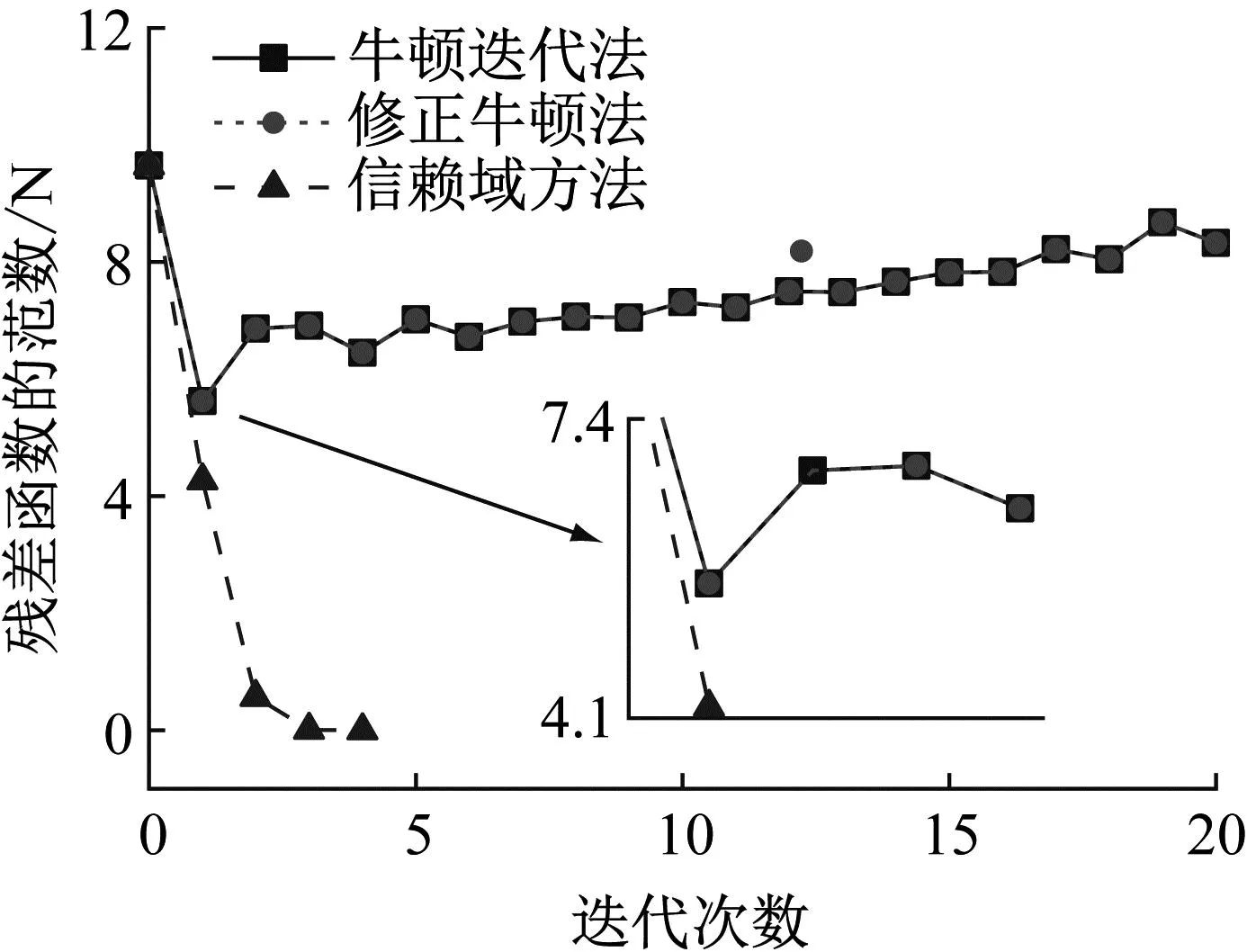
图6 不同方法下的迭代曲线

在样本功率谱密度的基础上,通过样本平均可以实现理论功率谱密度的估计。图7为结构在激励功率谱Sff(ω)=10 N2/Hz作用下的位移理论功率谱密度估计。其中MCS和E-PEM的样本数均为30。从图7可以观察到,MCS和E-PEM得到的结果一致,验证了E-PEM的正确性。在图7(b)中,非线性响应相比于线性响应,在96 Hz附近还出现了一个峰,此峰恰好是共振峰频率(32 Hz)的3倍,表明在随机激励作用下Jenkins非线性单元存在倍频现象。对于Jenkins单元所具有的这种非线性,文献[27]通过解析推导后,得出此类非线性系统的响应会产生额外奇数倍的频率分量(最小即为3倍),本文计算得到的现象与文献结果具有一致性。

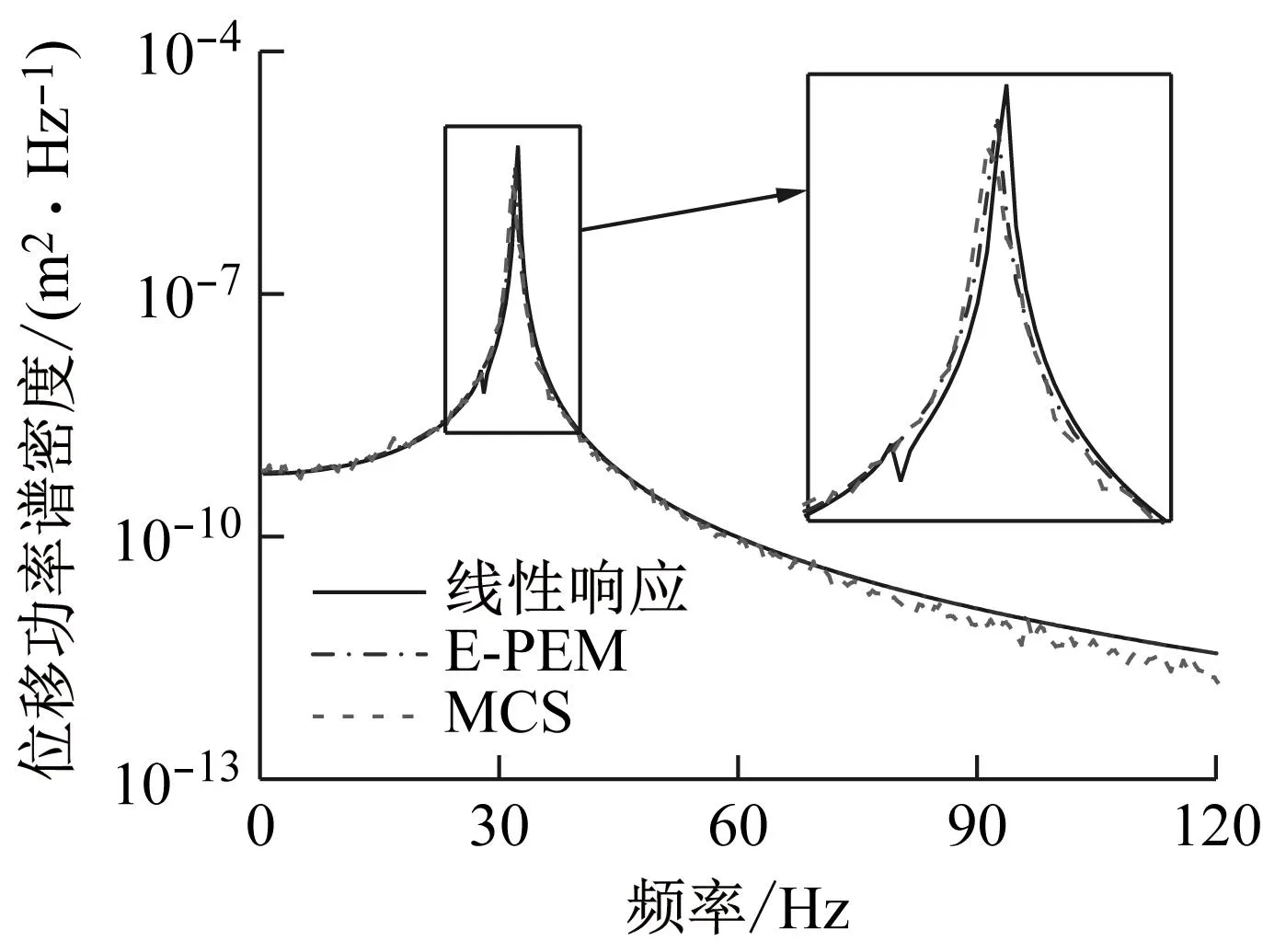
(a) 自由度1

3.2 螺栓连接组合结构随机振动响应分析

本小节将开展螺栓连接组合结构随机振动响应分析。图8为本文研究的螺栓连接组合梁结构,图8(a)为该组合结构的模型示意图,图8(b)为建立的简化有限元模型。该结构由两个相同的矩形等截面梁组成,矩形梁的尺寸为0.002 m×0.005 m×0.5 m,这两根梁的一端部分重叠并用螺栓相互固定,另一端采取固定约束。两个梁材料均为Q235钢,材料属性:密度为7 860 kg/m3,泊松比为0.288,弹性模量为212 GPa。

(a) 模型示意图

组合梁结构的有限元模型借助商业有限元软件Abaqus建立,以提供组装部件的线性动态响应。整个连接组合结构有限元模型共包含16个线性可剪切变形梁单元(B21单元),每个单元包含2个节点6个自由度,模型共54个自由度。模型的阻尼为瑞利阻尼,阻尼系数α和β分别为0.2和0.000 5。图8(b)中螺栓连接非线性涉及的参数为:接头预紧力Fjoint、界面摩擦因数μjoint和接头连接刚度kjoint。随机激励施加在组合模型左端的第四个节点处,观测点位于右端梁的第三个节点处。图8(b)中螺栓连接非线性涉及的参数及取值为:接头预紧力Fjoint=10 N,界面摩擦因数μjoint=0.1,接头连接刚度kjoint=5×103N/m。

图9为螺栓连接组合梁在Sff=1 N2/Hz随机激励作用下的响应功率谱密度。随机激励仅包含10～40 Hz的频率范围,用于激起结构的前两阶模态(分别为16.67 Hz和31.06 Hz)。图9(a)分别给出了线性和螺栓预紧力分别为10、20和50 N下,观测点的平均功率谱密度。图9(b)是共振峰处(10～40 Hz)的局部细节放大,可以看到,随着预紧力的减小,第二阶模态变得越来越不明显。

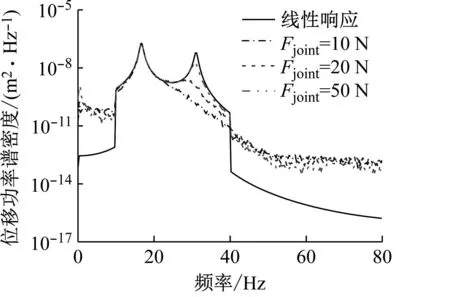
(a) 0～80 Hz范围的位移功率谱密度

为了进一步研究不同激励水平对螺栓连接梁结构滞回非线性的影响。本文在预紧力Fjoint=50 N、界面摩擦因数μjoint=0.1的情况下,对螺栓连接梁结构在激励强度Sff为0.1 N2/Hz,1 N2/Hz,5 N2/Hz和10 N2/Hz的情况进行了随机振动分析。图10为连接接头处的位移非线性力曲线。在激励强度Sff为0.1 N2/Hz的载荷强度下,由于接头界面力未达到临界滑移力(5 N),所以并未出现滞回效应。但是随着激励强度的增加,接头处的滞回效应逐渐显现且滞回环也随着激励强度的增加而逐渐扩大。

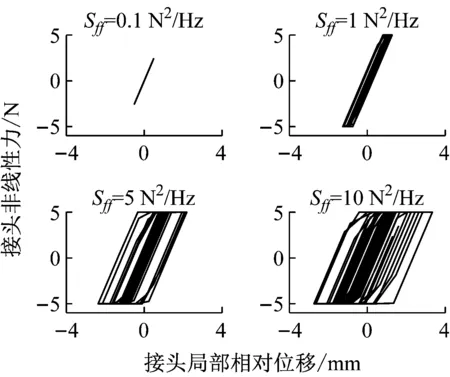
图10 接头处的位移-非线性力曲线

4 结 论

本文发展了实现考虑滞回效应的螺栓连接组合结构频域谱特性分析的E-PEM。将激励功率谱转化为复指数级数的展开形式,非线性随机振动响应功率谱分析转换为虚拟响应的乘积运算。引入时频变换(AFT)处理非线性本构在频域计算困难,进一步针对传统牛顿法处理非连续、非光滑本构时出现的收敛性问题,将非线性代数方程的求解问题转换为最优化问题并利用信赖域方法进行求解。在数值算例中,研究了含Jenkins模型非线性系统的随机振动响应功率谱特性,并采用MCS进行了对比验证,结果表明本文方法与MCS的结果吻合度较高,本文方法也为类似非线性动力学系统随机振动功率谱分析提供一种新的求解思路。

针对螺栓连接结构开展相关试验研究是一项富有挑战性工作。一方面原因是真实的螺栓连接结构中通常存在着多种耦合且不易分离的非线性[28](如:几何非线性、材料非线性、界面接触非线性等);另一方面,由于连接界面所具有的时变性和不确定性[29-30],也需要开展参数辨识、模型确认验证工作。本文研究目前所开展的螺栓连接组合结构频域随机振动分析仅进行了数值研究,通过与其他方法对比验证本文方法的正确性和有效性,针对螺栓连接结构开展随机振动试验验证有待更进一步的工作。