一种用于误差通道预辨识的气动冲击锤特性分析

李 锋,杨铁军,吴 磊,徐 阳,黎文科,李新辉,朱明刚

(1.哈尔滨工程大学 动力与能源工程学院,哈尔滨 150001; 2.哈尔滨工程大学 青岛创新发展基地,山东 青岛 266000)

船用机械设备工作时产生的振动传递给船体结构,是舰船产生水下辐射噪声、影响自身隐蔽性和生命力的主要因素。长期以来,研究人员开展包括被动[1-2]和主动[3-5]控制在内的多种减振技术的研究,以降低机械设备对船体的振动激励从而降低其结构声辐射。与传统的被动减振技术相比,主动减振技术不仅能有效地抑制机械设备的低频振动,还能适应外扰频率的变化,目前已经有成功应用的案例[6-7]。

主动减振系统设计中,对误差通道(从控制器输出到误差传感器输出之间的通道)的辨识是很重要的一个环节,它关系到主动控制系统的收敛性、稳定性和有效性[8-9]。但无论是离线还是在线辨识,一般是在主动减振系统于被控结构上完成安装之后进行,这在实验室环境中能比较方便地实施。在大型船舶机械设备主动减振系统的工程应用中:① 由于被控结构和主动减振系统的复杂性,对误差通道进行数学建模比较困难;② 受现场环境(空间和时间)所限,误差通道的辨识工作往往不能被很充分地完成;③ 在完成控制系统的现场安装后再进行误差通道辨识,一旦出现作动器与被控结构阻抗不匹配[10]问题很难补救。因此,如果能在主动减振系统现场安装前就得到误差通道比较准确的传递函数模型,不仅有助于主动减振系统的设计优化,还可以节省现场调试时间和降低系统的调试成本。

为此作者提出主动减振系统误差通道预辨识的方法[11],在现场采用锤击法获得被控结构的动力学特性,结合试验室得到的主动减振系统其他环节(如功率放大器、作动器等)的传递函数模型,获得实际主动减振系统误差通道的传递函数,在现场试验前对主动减振系统进行系统仿真、性能预测和设计改进。

由于舰船设备所在舱室往往比较紧促,现场测试位置的操作空间非常有限,采用传统力锤完成测试会存在一定困难。此外,对于大型船舶机械设备隔振系统,传统力锤的锤击能量可能不足以激起期望得到的动力学响应。而且测试过程易受人为因素的干扰,可重复性差,难以保证测试结果的准确性[12-13]。针对这一问题,作者所在课题组研制了一种通过高压气源驱动的便携式气动冲击锤[14](以后简称“气锤”),用于主动减振系统误差通道预辨识过程中现场被控机械设备隔振结构动力学特性的识别。测试时将气锤安装在主动执行机构(作动器)准备安装的位置,以高压气体推动其活塞组件,使活塞组件末端的锤头以一定的初速度与被控结构碰撞冲击。在锤头上方安装力传感器,测量冲击时的力信号,再结合安装于误差评价点的误差传感器的输出,即可测得被控机械设备隔振结构上作动器安装位置到误差传感器位置之间的传递函数。与传统的力锤相比,气锤不仅能够保证多次锤击时的位置、角度和锤击力大小的一致性,而且能方便地通过阀后压力设置调节冲击力幅的大小,因此可以提升误差通道预辨识的效率和质量。

本文首先对气锤工作时气体做功过程的热-机耦合模型和锤头冲击被控结构的动力学模型进行推导,并通过活塞组件运动过程的试验测试结果对所建模型进行检验;然后探讨几个可调的气锤结构动力学参数对锤头冲击速度的影响;最后对气锤冲击力的仿真和测试结果进行对比分析,并通过一个弹性结构的传递函数测试试验,验证利用所研制气锤获得主动减振系统中被控结构动力学特性的可行性。

1 气锤结构及工作过程

本文研究的气锤结构如图1所示。其外径为86 mm,高度为158.5 mm,质量为3.7 kg,主要由气锤缸体、活塞组件(包含活塞、锤头、力传感器)和复位弹簧等部件构成。

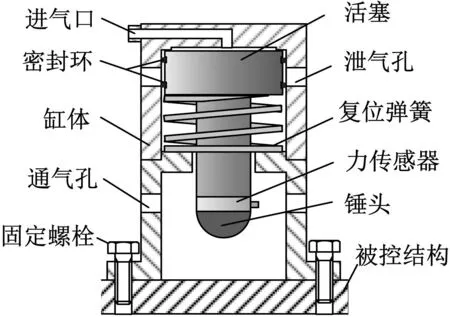
图1 气动式冲击锤结构示意图

整个气锤系统如图2(a)所示,包括气源(空压机)、稳压储气罐、减压阀和气锤本体。气锤的工作过程示意图如图2(b)所示,可分为初始状态、气体做功过程、锤头碰撞过程和复位过程四个阶段。其中初始状态时气锤处于静止状态,而复位过程中锤头已不再对被控结构产生激励,由此可知气体做功过程和锤头碰撞过程是影响测试结果的两个主要过程,因此后文将主要对它们进行建模分析。

(a) 气锤系统

2 气锤工作过程建模

2.1 气体做功过程

对气锤工作过程中高压空气的做功过程做如下假设:①气体为理想气体;②进气管和气锤缸体内的气体压力、温度和密度均匀分布;③做功过程为绝热过程。

减压阀后的气体体积流量QV与减压阀前后压力的关系如下[15]

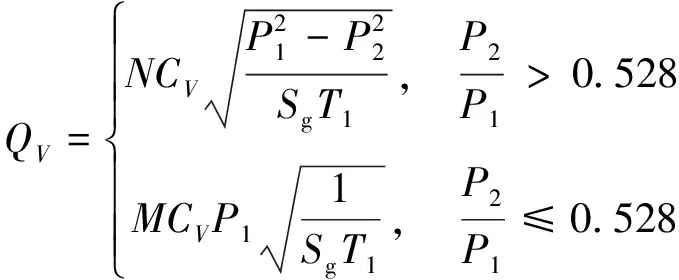
(1)

式中:N、M为常数;CV为流量系数;P1和P2分别为减压阀的进、出口压力;Sg为气体相对密度(空气:Sg=1.0);T1为减压阀进口的热力学温度。

将减压阀后和活塞前的气体视为控制体,在气体做功过程中,控制体的质量变化为

(2)

式中,m、ρ、V、T分别为控制体质量、密度、体积和温度。

减压阀开启后的极短时间内,气体做功过程相当于刚性容器的充气过程,由热力学第一定律有[16]

(3)

式中:E为控制体总能量;Q为控制体与外界交换的热量;hin、hout为进、出口气体的比焓,即单位质量气体的焓值;cin、cout为进、出口气体的流动速度;g为重力加速度;zin、zout为进、出口高度;min、mout为流进、流出控制体的气体质量;W为控制体与外界交换的功,δW=-PdV。

忽略控制体的宏观动能和重力势能,则控制体的总能量E等于控制体的内能U,且对U有:

U=H-PV

(4)

式中,H为控制体的焓。在气体做功过程中活塞上下表面之间存在一定程度的泄漏,设泄漏系数为l,单位为kg/s/Pa,则气体泄漏量δmout=lΔPdt,其中ΔP为气缸上、下表面的压力差。再结合绝热过程的假设,式(3)可简化为

dU=δminhin-δmouth+δW

(5)

式中,h=hout;δmin=QVρbΔt,ρb为外界环境中的空气密度。

控制体的内能变化

dU=hδm+mdh-VdP-PdV

(6)

式(5)与式(6)联立可得

mdh-VdP=δminhin-(δm-δmout)h

(7)

控制体焓H是其压力P和温度T的函数,式(7)可整理为

(8)

气体做功过程中活塞所受的外力如图3所示。

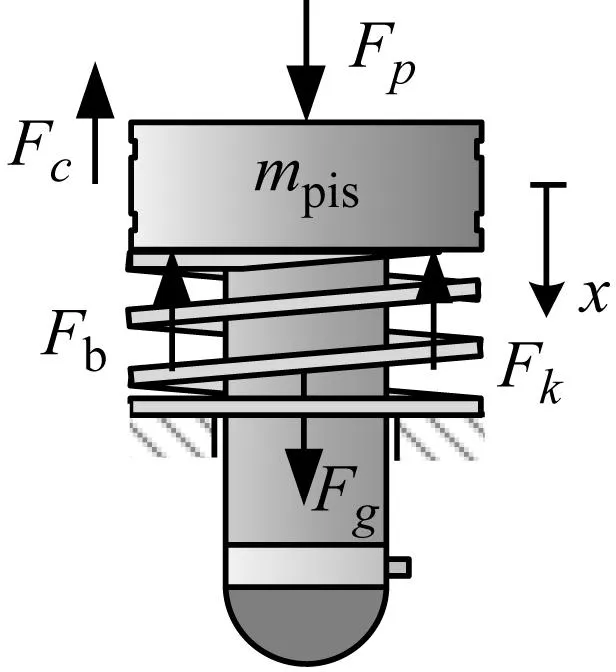
图3 活塞组件受力简图

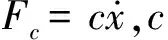
气体做功过程中活塞组件的运动微分方程为

(9)

所以气锤气体做功过程的热-机耦合数学模型为

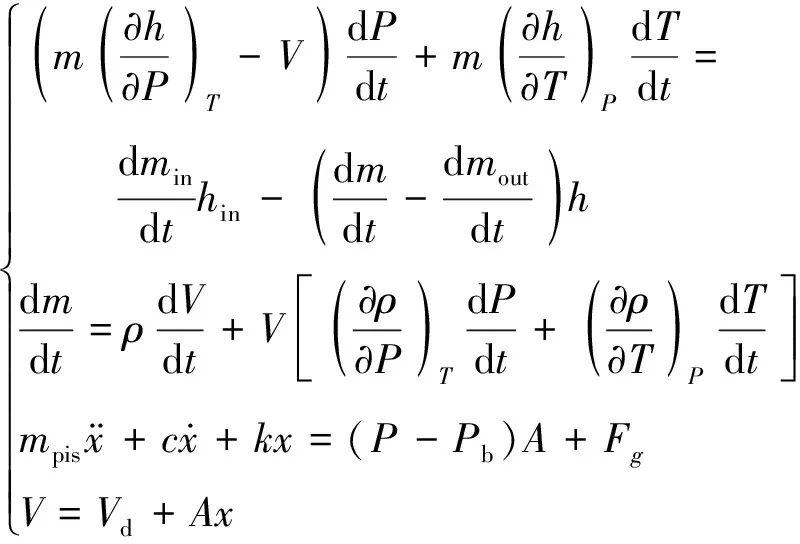
(10)

式中,Vd为气锤缸体内的死区容积。

2.2 锤头与被控结构的碰撞过程

活塞上表面通过泄气孔后,其上下表面压差为零,气体做功过程结束。此后活塞组件做减速运动,其运动微分方程为

(11)

若锤头能够到达被控结构表面,且其速度不为零,那么两者将会发生碰撞,碰撞过程可以简化为两个质体的对心碰撞。假设两质体的曲率半径分别为r1和r2,根据Hertz接触理论[17-18],它们的Hertz刚度可表示为

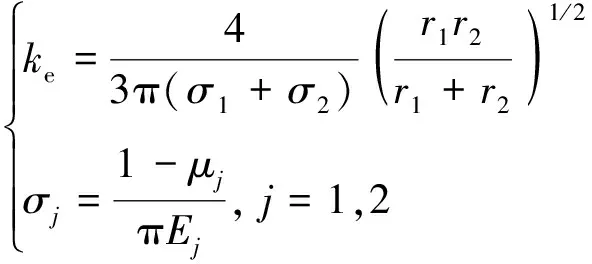
(12)

式中:E1、E2分别为两个质体的弹性模量;μ1、μ2分别为两个质体的泊松比。

则两个质体碰撞过程中的冲击力可以表示为

Fi=keλq,q=1.5

(13)

式中,λ为两个质体间的相对变形量。

将两个质体的相对运动速度记为vr,有

(14)

式中,me为两个质体的等效质量。假设它们的质量分别为m1、m2,则me=m1m2/(m1+m2),此处m1=mpis。

碰撞发生后,当两个质体的相对速度vr=0时,两个质体的相对变形量λ达到最大值,即:

(15)

式中,vr0为两个质体的相对初速度。

将式(14)与式(15)联立,可得两个质体的相对速度vr与相对变形量λ的关系为

(16)

对式(16)积分可得

(17)

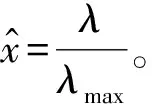
假设碰撞的压缩阶段与恢复阶段的接触时间相同,可得两个质体碰撞时的接触时间为

(18)

由此可知,当锤头与被控结构的材料属性确定后,它们碰撞时的最大冲击力Fi和接触时间ti均由相对初速度vr0决定。

3 仿真与试验分析

基于前文的理论模型对气锤的工作过程进行仿真分析和试验测试,其中涉及的主要物理参数如表1所示。

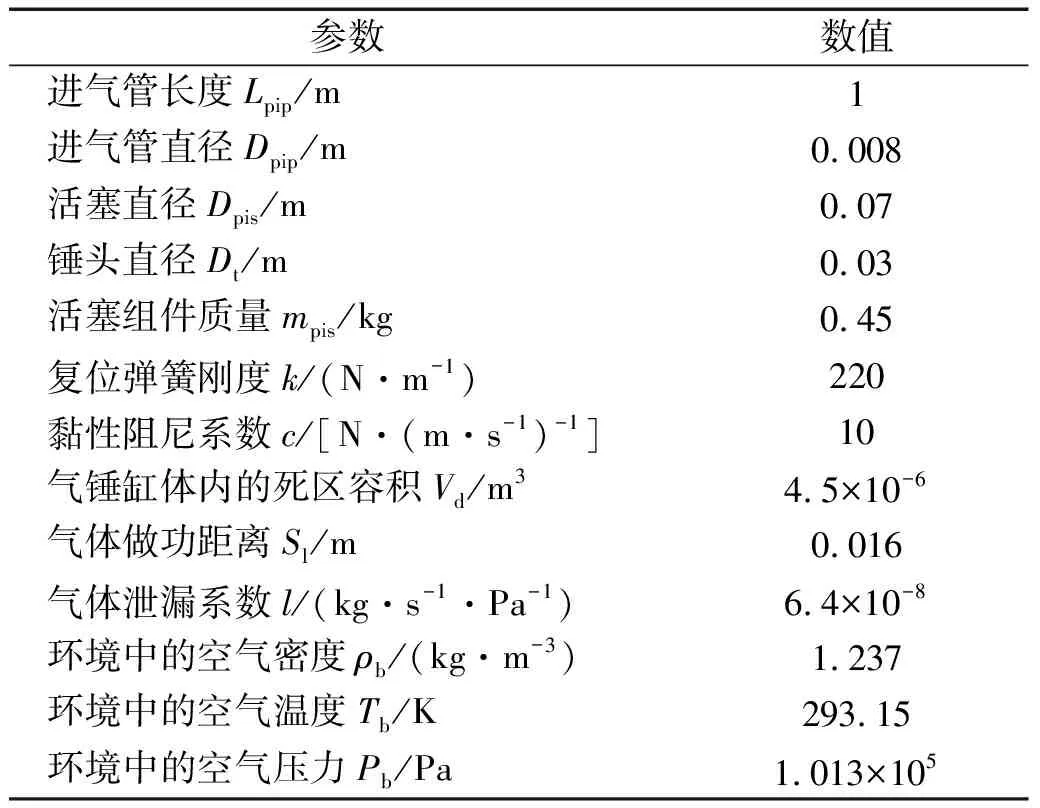
表1 气锤主要物理参数

3.1 气体做功过程

气体做功过程中活塞组件的加速度、速度以及气缸内压力随时间的变化关系如图4所示(为了更好地展示细节,其横坐标时间采用对数坐标)。其中,减压阀的阀后压力P2设置为0.4 MPa,此时气体的体积流量QV约为0.38 m3/min。

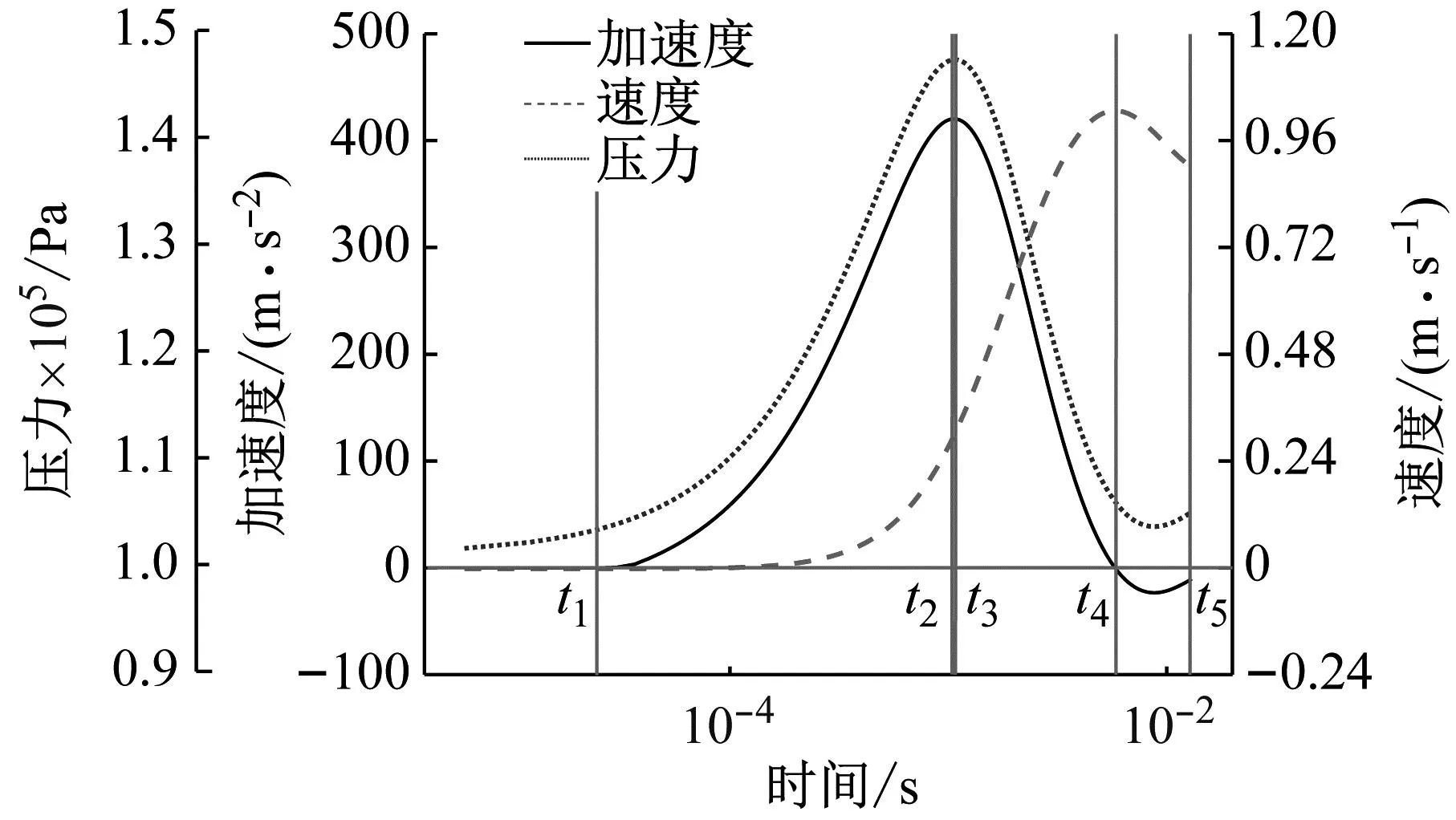
图4 活塞组件加速度、速度和气缸内的压力

由图4可知,气体做功过程中活塞组件的运动情况可以描述如下:

(1)t1时刻前,活塞组件保持静止状态,随着高压气体进入气缸,缸内压力不断上升。

(2) 从t1时刻开始,活塞组件的加速度和速度在极短的时间内快速增大,同时对外做功。在t2时刻前后,活塞组件加速度和缸内压力相继达到最大值。到t3时刻以后,控制体体积快速增长,高压空气带入的内能小于活塞组件对外所做的体积功,缸内压力开始变小。

(3) 随着缸内压力的下降,活塞组件加速度继续变小,到t4时刻,活塞组件受力达到平衡,此时活塞组件的加速度为零,其运动速度达到最大值。随后复位弹簧的回复弹力和摩擦力大于活塞上下表面的压差和重力,活塞组件开始减速。在活塞组件的反向加速度到达第一个极值点后,控制体做的体积功小于进气带入的内能,缸内气体压力会有所回升,活塞组件反向加速度变小。

(4) 到t5时刻,活塞上表面通过泄气孔,气体做功结束,随后活塞组件做给定初速度的减速运动。

在气锤活塞组件锤头的位置安装加速度传感器,测量气体做功过程中活塞组件加速度的变化情况。与前文的仿真分析过程一样,此时减压阀输出气压也设为0.4 MPa,试验测试与仿真计算结果的对比如图5所示。

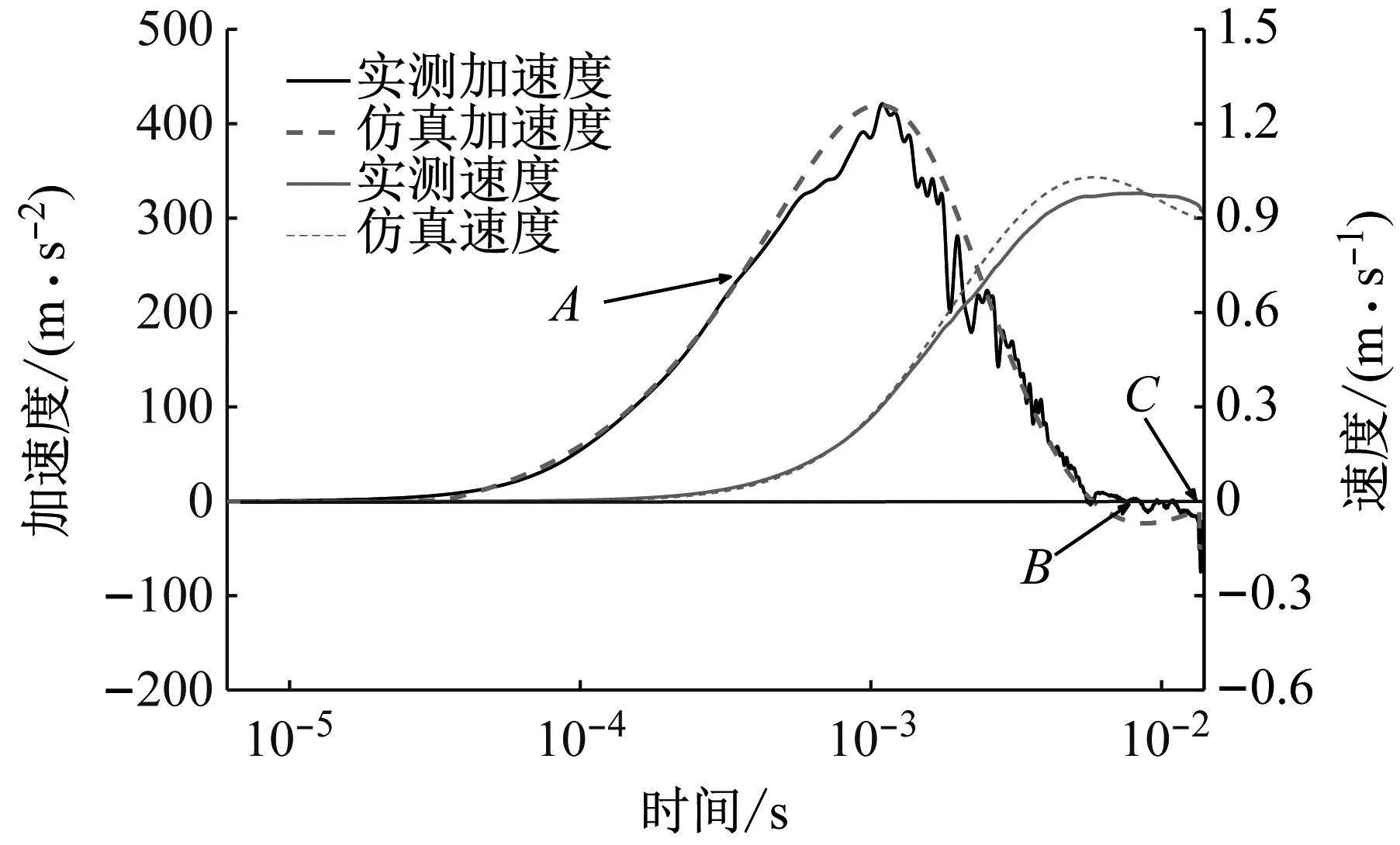
图5 活塞组件加速度和速度试验和仿真结果对比

由图5可知,气体做功过程的仿真结果与试验测试结果较为吻合,曲线整体趋势一致,存在的差异主要体现在从A时刻起到气体做功结束的时间段内。在这一期间,活塞组件的仿真加速度曲线较为平滑,而实测曲线存在一定波动,这是由实际过程和仿真过程泄漏系数不同导致的。实际的气锤活塞仅靠两道密封环与气缸壁密封,随着活塞位置改变,做功过程中的泄漏系数也会发生改变。到图中B时刻前后,活塞第一道密封环下沿到达泄气孔的边缘,气缸气密性进一步降低。到C时刻活塞第一道密封环上沿到达泄气孔,缸内压力突降,活塞组件受到的反向加速度突然变大,气体做功过程结束。泄漏系数在这一过程中的变化十分复杂,为简化仿真模型,仿真中将泄漏系数设为了定值。

3.2 活塞组件冲击初速度影响因素分析

在识别船舶机械设备的动力学特性时,需要恰当选择冲击力的峰值和冲击时间的长短才能保证测试结果的质量。根据前文所述,碰撞初速度vr0是影响冲击力峰值和冲击时间的关键参数,因此本节对从减压阀开启到锤头与试件碰撞前的活塞组件运动过程进行仿真。仿真中将减压阀的阀后压力P2设置为0.7 MPa,并分析复位弹簧刚度、活塞与气锤缸壁之间的黏性阻尼系数和气缸内的死区容积对锤头碰撞初速度的影响。将这三个参数的初始值分别记为k0、c0和Vd0,逐个改变各参数(当其中一个参数改变时,另外两个参数保持为初始值),得到仿真结果如图6所示。

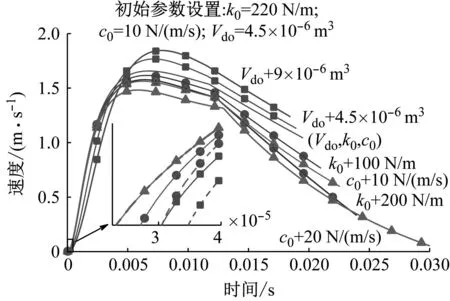
图6 单一改变弹簧刚度、阻尼或死区容积对锤头碰撞初速度的影响

图6中,气体做功初期极短时间内活塞组件速度的变化曲线被绘制于局部放大图中(横纵坐标均取对数坐标),以便观察活塞组件在该阶段的运动状态。由图6可知:

(1) 随着复位弹簧刚度的增加,活塞组件开始运动的时间推后,这是因为推动活塞运动所需的气压增大,建立气压所需时间变长。同时活塞组件所能达到的最大速度变小,从而碰撞初速度减小;

(2) 阻尼变化对活塞组件开始运动的时间影响不大,只是在活塞组件运动起来之后:小阻尼时活塞组件的最大速度变大,碰撞初速度也会增大;大阻尼时活塞组件的最大速度减小,活塞组件减速运动阶段的速度衰减会被加快。图中显示当阻尼为30 N/(m/s)时,在锤头到达试件之前活塞组件的速度已经衰减为0,此时碰撞不会发生;

(3) 气缸内的死区容积越大,建立缸内气压所需的时间越长(会导致气锤的响应速度变慢),但活塞组件所能达到的最大速度以及锤头碰撞时的初速度却越大。

4 气锤冲击力和动力学参数辨识结果对比

分别测量气锤在阀后压力为0.6 MPa和0.7 MPa时尼龙锤头冲击弹性钢质结构时的冲击力,与仿真结果的对比如图7和表2所示。

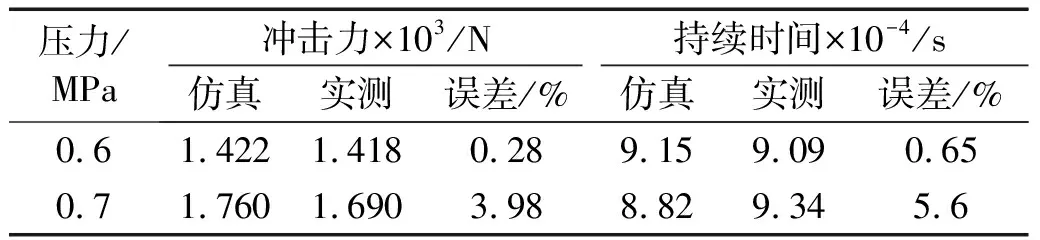
表2 气锤冲击力仿真和实测结果

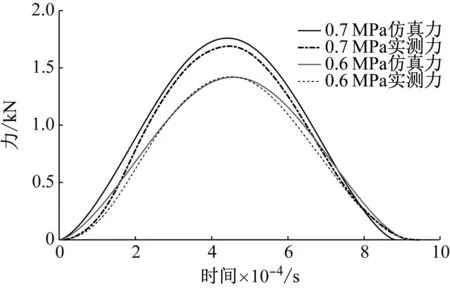
图7 气锤实测冲击力与仿真结果的对比

由图7可知,气锤冲击力仿真曲线和实测曲线形状吻合较好,但仍存在一定差异,这些差异与碰撞模型中忽略了结构的迟滞阻尼和恢复系数等因素有关。从式(13)中可以看出,仿真模型并未考虑材料阻尼,且计算冲击时间时也采用了压缩时间与恢复时间相同的假设,因此仿真所得的冲击曲线会与实测曲线会存在不同。但从图7中的对比曲线和表2中的误差数值来看,实测和仿真结果的差异并不显著。

除冲击力幅值和冲击时间外,冲击信号的可重复性是影响船舶机械设备动力学特性测试质量的另一个关键因素。为了验证气锤冲击力的可重复性,分别以铝锤头和尼龙锤头在阀后压力0.6 MPa驱动下进行了多次冲击试验,测得的冲击力结果如图8所示。从图8可见,当锤头材质为铝质时,其冲击时间约为尼龙锤头的一半,最大冲击力幅值约为尼龙锤头的3倍多,但两种锤头的冲击力信号均保持着良好的可重复性。

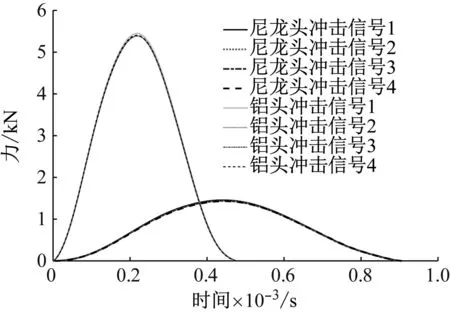
图8 气锤冲击力的可重复性验证

最后以气锤作为冲击力源,针对该弹性结构进行结构动力学参数的辨识,并与用传统的力锤锤击同一点的辨识结果进行对比,试验现场和对比结果如图9和图10所示。

图9 气锤冲击试验

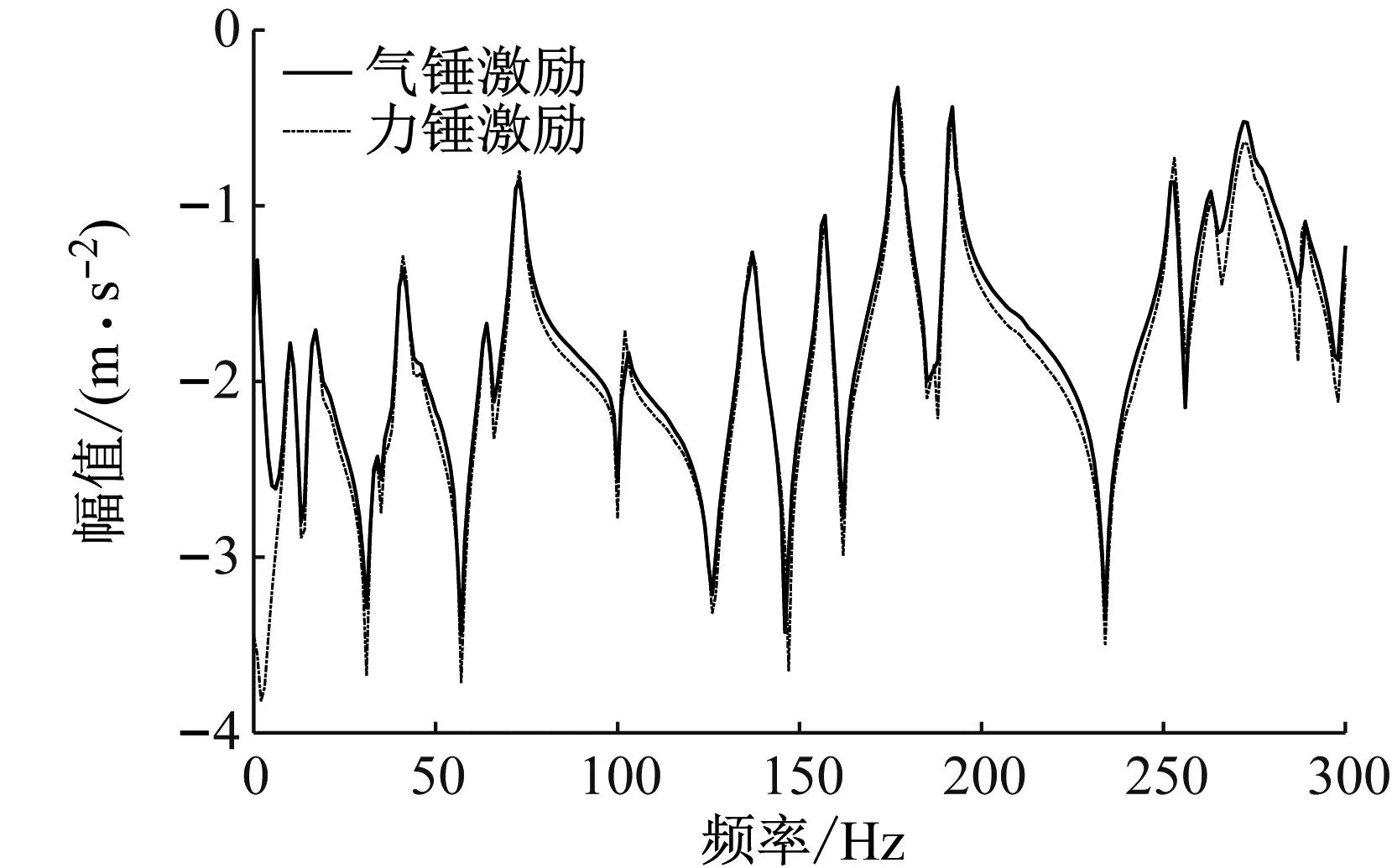
(a) 幅频响应

从图10可以看出,两种气锤激励弹性结构得到传递函数幅频和相频曲线基本一致,这意味着采用本文研制的气锤作为冲击力源进行被控结构误差通道传递函数的预辨识是可行的。

5 结 论

本文针对一种用于舰船机械设备的主动减振系统误差通道预辨识的便携式气动冲击锤开展研究。通过对气体做功过程和冲击过程的数学建模,对比分析了活塞组件运动过程的仿真和试验测试结果,讨论了复位弹簧刚度等结构动力学参数对锤头冲击速度的影响。最后对气锤冲击力的测试和仿真结果进行了对比分析,并用气锤对一弹性结构进行传递函数测试,验证了气锤对结构动力学特性参数测试的可行性和有效性。研究结论如下:

(1) 增大气锤复位弹簧刚度和阻尼都会减小活塞组件所能达到的最大速度,同时加快活塞组件减速运动阶段的速度衰减,减小锤头的碰撞初速度。

(2) 增大死区容积会导致气锤的响应速度变慢,却能有效提高活塞组件的最大速度进而提高锤头的碰撞初速度。

(3) 气锤的冲击力曲线是典型的半正弦曲线,冲击力幅值可以方便地通过调节压力来调整且可重复性好,气锤对结构动力学参数的辨识结果与传统力锤的辨识结果吻合良好,可以满足船舶机械设备主动减振系统误差通道预辨识的需求。