考虑滚动体滑移的全陶瓷角接触球轴承非线性动态特性分析

张 珂,张立奇,王 展,高刘旺

(1.沈阳建筑大学 机械工程学院,沈阳 110168; 2.沈阳工业大学 机械工程学院,沈阳 110870)

陶瓷角接触轴承具有良好的耐磨性和抗热变形能力,因此能够保证转子系统在高速运转的工况下具有稳定的回转精度[1]。陶瓷滚动体由于高刚度的特性,在承受大载荷时变形量远远小于钢制轴承滚动体,陶瓷滚动体的最大旋转速度和打滑周期都会发生变化。尤其是当其经过承载区时,其在外圈沟道上会发生滑移现象[2]。此时陶瓷滚动体的磨损加剧,滑移产生的热量会影响润滑环境,导致滚动体的滑移运动加剧进而影响轴承的动态特性。持续的滑移运动会导致滚动体和外圈擦伤,严重影响到陶瓷轴承的回转精度和寿命[3]。因此,研究滚动体发生滑移运动时的全陶瓷角接触球轴承非线性动态特性具有重要意义。

为了更加准确地描述轴承中的接触关系和运动机理,近年来众多学者针对不同工况和不同影响因素进行了轴承动力学研究。Han等[4-5]考虑球的旋转与内外圈沟道的赫兹接触、球与保持架的不连续接触以及弹流润滑等引起的离心和陀螺效应,分析了径向载荷对轴承滑移的影响。Gao等[6-8]考虑轴承运动学、滚动体与滚道之间的赫兹接触、滚动体与保持架之间的相互作用、流体润滑以及热效应的综合模型来研究预测过滑和打滑机理,并给出了润滑油流量对打滑程度的影响规律。Wang等[9]建立了考虑滚动体与滚道、保持架和润滑剂相互作用的角接触球轴承滑动动力学模型,分析了轴向载荷对滚动体滑移的影响。Liu等[10]建立了滚动轴承的滑动动力学模型,研究了保持架的径向载荷、内圈加速度和质量块之间的连接刚度对轴承滑动的影响。Deng等[11]建立了考虑保持架旋转和弹流润滑的球轴承改进动力学模型,研究了保持架旋转、球的滑动和轴承套圈振动之间的相互作用机理。Wang等[12]提出了一种考虑轴承变形和滚动体与内滚道分离的球轴承非线性动力学改进模型,研究了不同因素下轴承变形、接触特性和保持架滑移的变化规律。Liu等[13-14]建立了考虑滚动体与滚道及保持架之间相互作用的轴承滑动动力学模型,分析了滚动体数、内半径、润滑油密度和黏度、过盈配合、径向载荷等因素对滚动体打滑现象的影响。Wen等[15]建立了角接触球轴承的多自由度故障动力学模型,揭示了不同尺寸和位置角度的外滚道故障对轴承动态特性的影响。Ma等[16]提出了考虑润滑牵引力和轴承组件动态特性的四点接触球轴承非线性动力学模型,给出了轴承工作中减少滑动损伤的方法。可见关于轴承滚动体接触机理和打滑行为的研究已经取得了一定的进展,这些研究近乎完整地描述了滚动轴承的滑移行为机理和动态特性。但是全陶瓷角接触球轴承在承受载荷时发生的变形量远小于钢制轴承,通过赫兹理论假设来计算接触力会产生一定的偏差,在进一步做动力学分析时,会进一步放大这一部分误差。同时较小的变形量导致滚动体经过承载区时在滚道中发生滑移,此时滚动体受到的滑动摩擦力与正常接触时的滚动摩擦力相差甚远。因此为了更加准确地描述全陶瓷角接触球轴承的动态特性,考虑滚动体滑移行为进行全陶瓷角接触球轴承的动力学分析具有重要的研究意义。

本文分析了全陶瓷角接触球轴承滚动体滑移接触机理,在接触力学基础上计算了滑移接触参数,与正常接触时的接触参数进行了比较并分析了两者的变化规律。建立了考虑滚动体滑移行为的全陶瓷角接触球轴承动力学模型。搭建了全陶瓷角接触球轴承转子试验台验证了模型的准确性,通过时频域分析和轴心轨迹图分析了轴承系统的振动特性,并通过混沌分析理论进行了稳定性和周期性分析。

1 全陶瓷角接触球轴承滑移接触机理

为了分析全陶瓷角接触球轴承的滑移运动,由轴承几何变化入手考虑受力情况进行拟静力学分析,然后考虑运动学因素和力学分析进行轴承动力学分析。考虑到全陶瓷角接触球轴承的内外圈滚道结构,在陶瓷滚动体发生极小量的形变时滚动体会发生滑移运动如图1所示。图1中:ωb为滚动体转动角速度;A为滑移前滚动体与外圈接触点;A′为滑移后滚动体与外圈接触点;O为轴承外圈中心点。此时陶瓷滚动体与外圈接触面积增加,而相应的正载荷受滑移角度的影响变小,接触力也因此变小[17]。

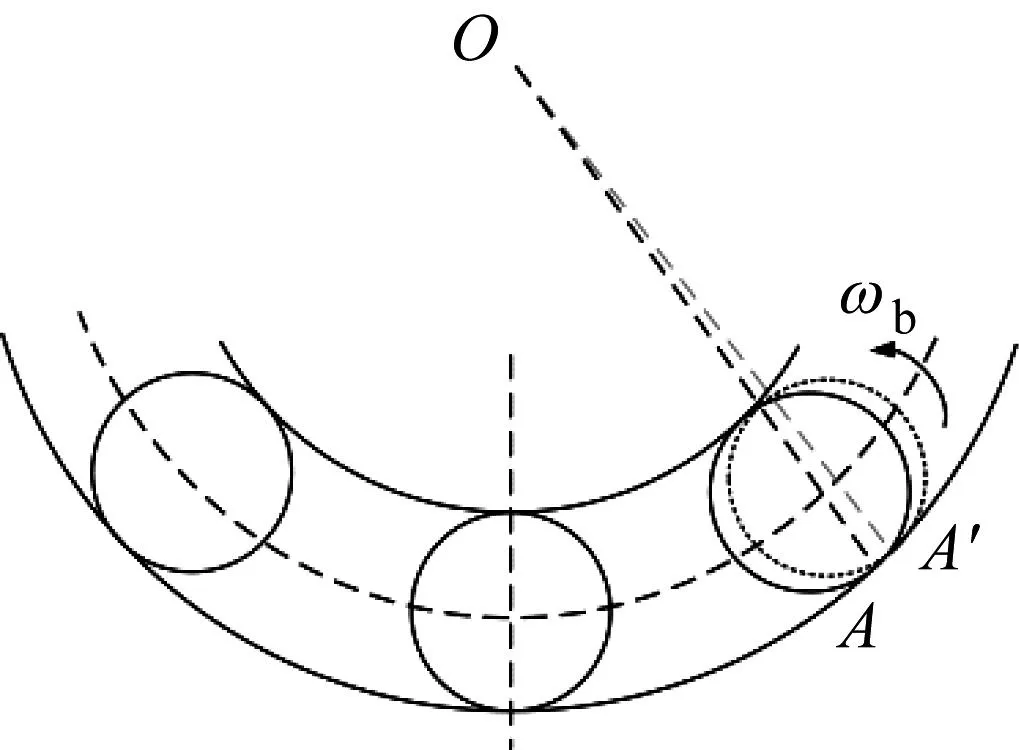
图1 滚动体滑移示意图

在全陶瓷角接触球轴承中,轴承内外圈与滚动体均属于高硬度高刚度材料,因此在运转过程中,不考虑打滑的情况下滚动体与内外圈均属于赫兹点接触。当仅受到竖直方向载荷的情况下,陶瓷滚动体与外圈接触的局部模型中接触点扩展成为圆形。接触应力在接触区域上方呈椭圆形式分布[18],靠近中心处接触应力最大,靠近接触边界处接触应力最小。陶瓷滚动体与外圈接触关系如图2所示。其中,r11=r21为滚动体半径,r12为外圈曲率半径,r22为外圈滚道曲率半径。

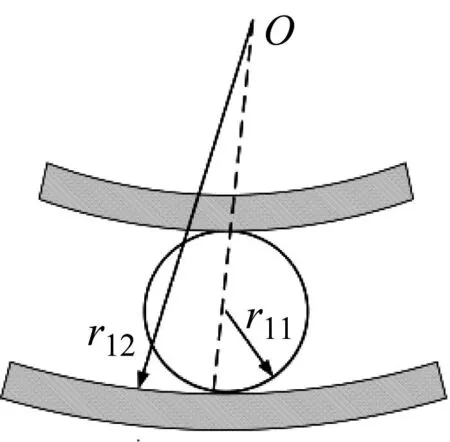
(a) 轴向接触示意图

滑移接触参数示意图如图3所示。图3(a)为轴承轴向上滚动体与内外圈的接触区示意图,图3(b)为轴承径向上的外圈接触区示意图。

(a) 轴向视图

滚动体和轴承外圈的总变形如式(1),轴承滑移接触刚度如式(2)

(1)

(2)

式中:Γ(e)为椭圆第一类积分;Π(e)为椭圆第二类积分;∑ρ为接触体之间曲率和;E1、E2分别为滚动体和轴承外圈的弹性模量;ν1、ν2分别为滚动体和轴承外圈的泊松比。

2 全陶瓷角接触球轴承动力学建模

考虑滑移运动对轴承振动特性的影响,需要分析轴承受力状态。轴承运转过程中滚动体受力状态如图4所示。分析可知滚动体受力关系如式(3)

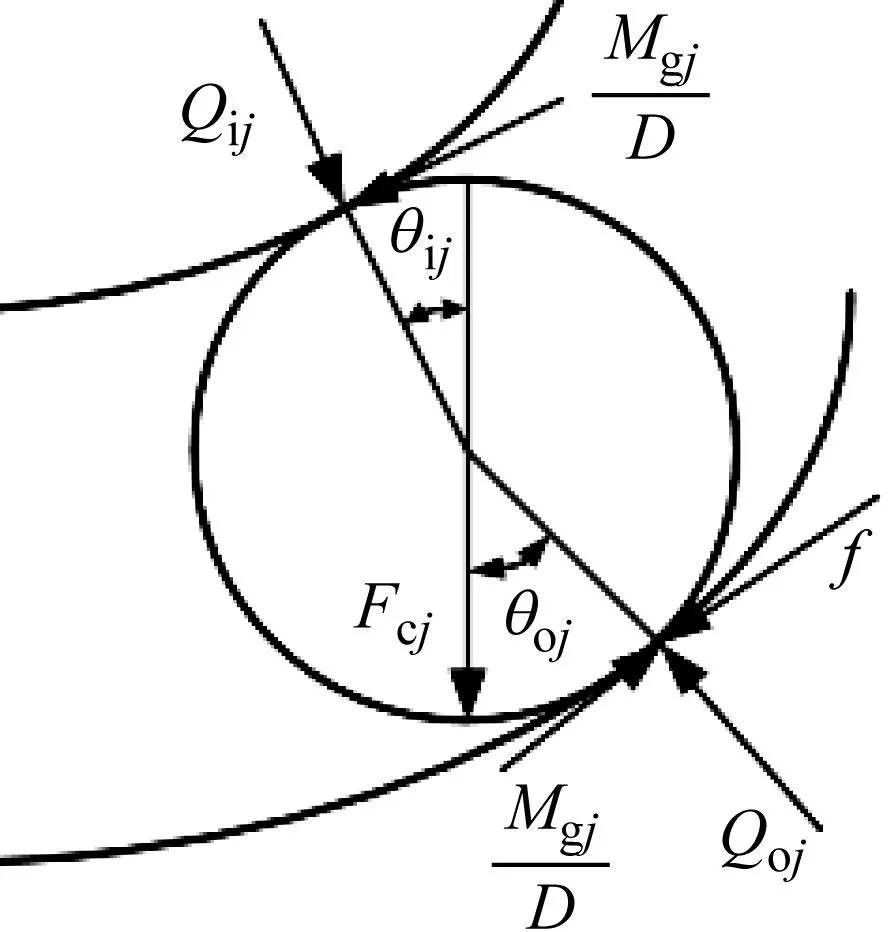
图4 滚动体受力示意图

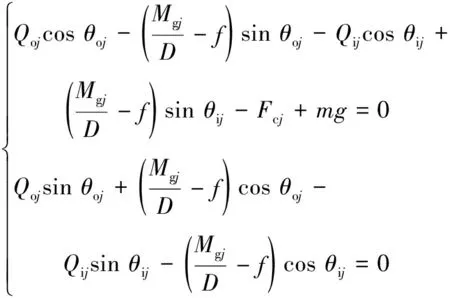
(3)

式中:Qij为内圈接触力;Qoj为外圈接触力;θij为内圈接触角度;θoj为外圈接触角;Fcj为滚动体离心力;m为滚动体质量;Mgj为陀螺力矩;D为滚动体直径。f为滑移摩擦力由滚动体与外圈的滑动摩擦力fbs和滚动体与油膜之间的油膜阻力fbo组成,可由式(4)、(5)计算得到

(4)

(5)

式中:ΔU为滑动速度;η为油膜黏度;h为油膜厚度。由公式可知影响轴承滑移摩擦力的因素包括外圈摩擦因数、接触变形、相对滑动速度、润滑油黏度和油膜厚度。其中各参数的变化共同作用影响滑移摩擦力的大小,随着载荷增加fbs逐渐增大,η逐渐增大,fbo逐渐增大。当滑移摩擦力增大时生热量增加导致η减小,摩擦系数减小,相对滑移速度增加。可见轴承内部滑移接触关系会受到元件之间摩擦力以及相对滑移速度的影响。

第三，制度自信是根本保障。根本保障在于坚持和发展中国特色社会主义制度。社会制度实际运行合理与否，并不能简单地将“个体生活”的好坏作为评判标准。西方现代文明的一个根本性缺陷就是简单地将“社会制度”还原为“个体制度”，而彻底地遗忘了社会属性。当代中国是一个有着近14亿人口的大国，中国共产党实现自己的执政理念与执政目标，面对的国际国内环境越来越复杂，肩负的繁重历史使命远超出现代西方选举类型政党。可以说，这个制度是对西方制度的超越。

作用在轴承内圈的力如式(6)

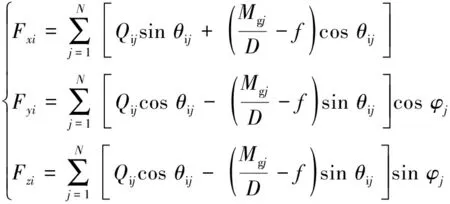
(6)

式中,φj为滚动体位置角。轴承内圈拟合刚度如式(7)

(7)

同理计算陶瓷轴承外圈及滚动体刚度,最终合并得到轴承拟合刚度kb。轴承单元能量计算如式(8)～(10)。

FcosωsΔy+FΔz-f[x(cosφjsinωs+

sinφsinωs)+y(cosφjcosωs)+

(8)

kb(x2+y2+z2)}

(9)

(10)

式中:T为轴承动能;V为轴承势能;D为损耗能量;mpi为轴承单元质量;I为自转动惯量;J为公转动惯量。

拉格朗日能量法迭代方程如式(11)

(11)

式中:qi为对应自由度上的位移分量;Qi为对应方向的外力。最终得到轴承动力学模型如式(12)

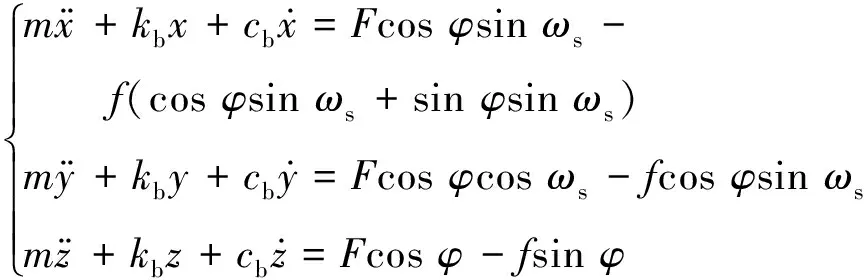
(12)

3 仿真分析

3.1 全陶瓷角接触球轴承接触参数分析

根据本文中提出的全陶瓷角接触球轴承接触模型进行仿真计算,轴承参数如表1所示。可以得到陶瓷滚动体接触变形随径向载荷变化曲线,如图5所示。由曲线变化可知,滑移接触变形随径向载荷的增加呈增大趋势,当载荷达到1 000 N时最大接触变形相差17.741 μm。与正常接触的情况相比,接触变形在整个过程中平均减小35%,说明陶瓷滚动体滑移导致的接触变形相比于传统模型计算的数值会产生不可忽视的差异。

表1 轴承仿真参数

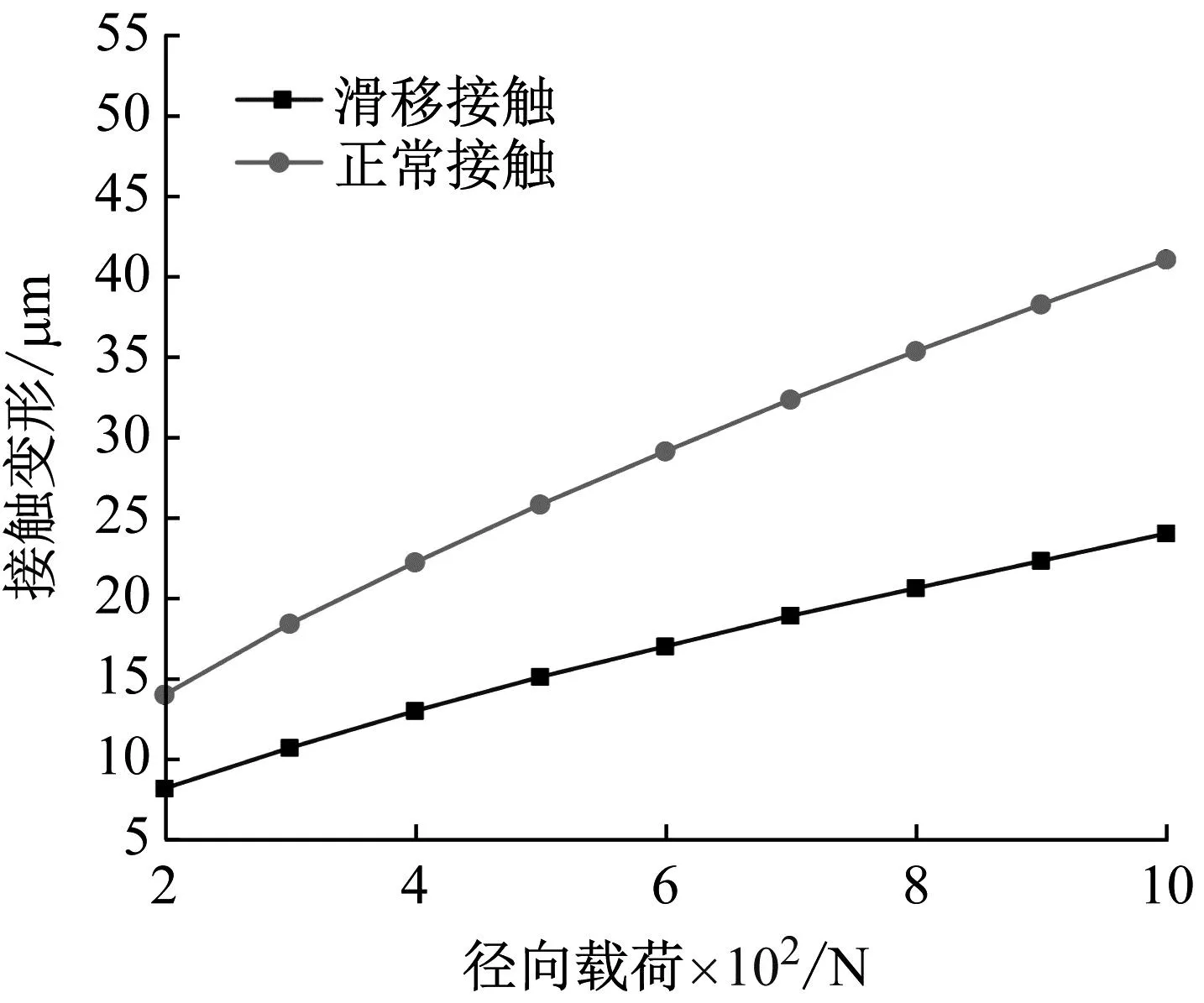
图5 径向载荷对接触变形的影响

以全陶瓷角接触球轴承转3 000 r/min为例,接触面积随径向载荷变化关系如图6所示。随接触载荷的增加,滑移接触面积呈增长趋势,与正常接触相比接触面积明显增加。这是因为在滚动体发生滑移的过程中产生了偏移角,滚动体的滚动分解为自旋运动和沿着轴承外圈的滑动,接触面积在滑动过程中增加,这也是全陶瓷角接触球轴承与金属轴承相比振动变小的主要原因之一。

图6 径向载荷对接触面积的影响

通过不同接触方式计算轴承接触力随径向载荷变化的曲线图如图7所示。分别对比了陶瓷材料正常接触、滑移接触和赫兹接触下的计算结果。可以看出三者计算结果均为随径向载荷的增加轴承外圈的接触力线性增大,其中通过赫兹接触公式计算的结果最小,这是由于赫兹接触理论中假设物体为完全弹性体并且接触面为均匀面接触,而陶瓷材料的弹性模量远大于一般金属材料,进而导致计算的接触力整体偏小。当陶瓷滚动体发生滑移时,接触力被滑移造成的偏转角分解为两个自由度上的分量,其中一部分与滑移摩擦力相抵消,最终导致接触力小于正常接触下的计算结果。

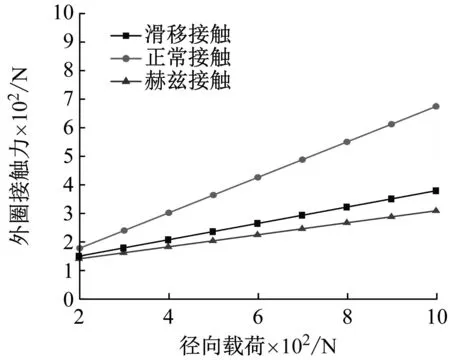
图7 径向载荷对接触力的影响

3.2 全陶瓷角接触球轴承振动特性分析

图8 轴承动刚度时变曲线

为了分析全陶瓷角接触球轴承在承受径向载荷时的振动特性,本文建立了径向载荷作用下滚动体发生滑移时的轴承动力学模型,通过四阶龙格库塔法对建立的轴承动力学模型进行求解,可以得到不同参数影响下的轴承振动特性。

全陶瓷角接触球轴承振动位移随转速的变化曲线如图9所示。图9分别展示了径向载荷为200 N,转速为1 200 r/min,2 400 r/min和3 200 r/min时的径向振动时域图以及通过0～10 s内振动位移计算结果所绘制的频域图和轴心轨迹图。由图中曲线可知轴承呈现周期性振动,稳定振动幅值分别为2.337 μm,6.175 μm,9.014 μm。由图9中时域图可以看出,随着转速的增加振动幅值增加,但同时受转速的影响轴承滑移速度随之增加,滑移现象导致轴承刚度增加因此振动波形幅值逐渐减弱至稳定值。

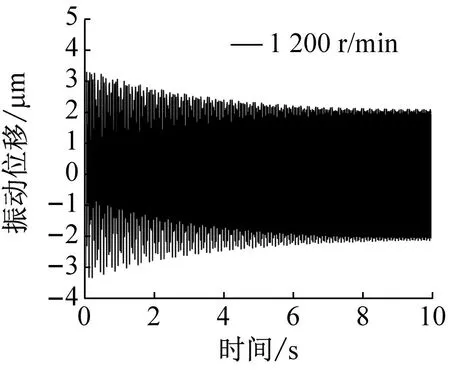
(a) 转速为1 200 r/min时域图

随着转速增加,轴承振动位移随之增大。频域图中的各峰值分别对应不同特征频率,其中一阶频率对应在承载区滚动体冲击时的振动频率,二阶频率对应转动频率。由图9曲线可知,随着转速的增加,转动频率随之增加,滚动体滑移的特征频率不变,但是各频率对应的振动幅值均增大。由轴承轴心轨迹图可以看出,轴承在运转过程中呈椭圆形运动,这是由于径向载荷的施加导致轴承承载区受力增加。同时在滚动体进出承载区时发生滑移,轴承总体振动减小,因此呈现扁形椭圆状趋势。随着转速增加滑移现象更加剧烈,轴心轨迹在滚动体进入承载区和离开承载区时形变最为明显,因此轨迹逐渐呈现对角线对称的椭圆形状。

全陶瓷角接触球轴承在径向载荷为300 N,500 N和1 000 N下的振动曲线如图10所示。由图10可知,在轴承运转的初始阶段振动幅值较大,随时间慢慢减低并稳定至有效幅值。这是由于受轴承径向载荷的影响轴承振动随着增大,但同时随着滚动体在运转过程中发生滑移轴承整体刚度增大,振动波形幅值逐渐减小并稳定。当转动速度为3 000 r/min时,随着径向载荷的增大,轴承振动位移呈现先增大后减小的趋势,最终在径向载荷为1 000 N时稳定于19.831 μm。在300～500 N阶段,随着径向载荷的增大,轴承承载区中滚动体与内外圈滚道之间的接触力增加,振动位移随着变大。在500～1 000 N阶段,随着轴承载荷的增加滚动体在承载区的滑移运动更加明显,轴承径向载荷沿滑移角分解为切向力和径向力两部分,此时参与轴承接触的为径向力部分,因此滚动体与内外圈滚道之间的接触力变小,轴承振动减小。在轴承径向载荷超过1 000 N后,轴承径向载荷达到滚动体控制临界点,振动逐渐趋于稳定。

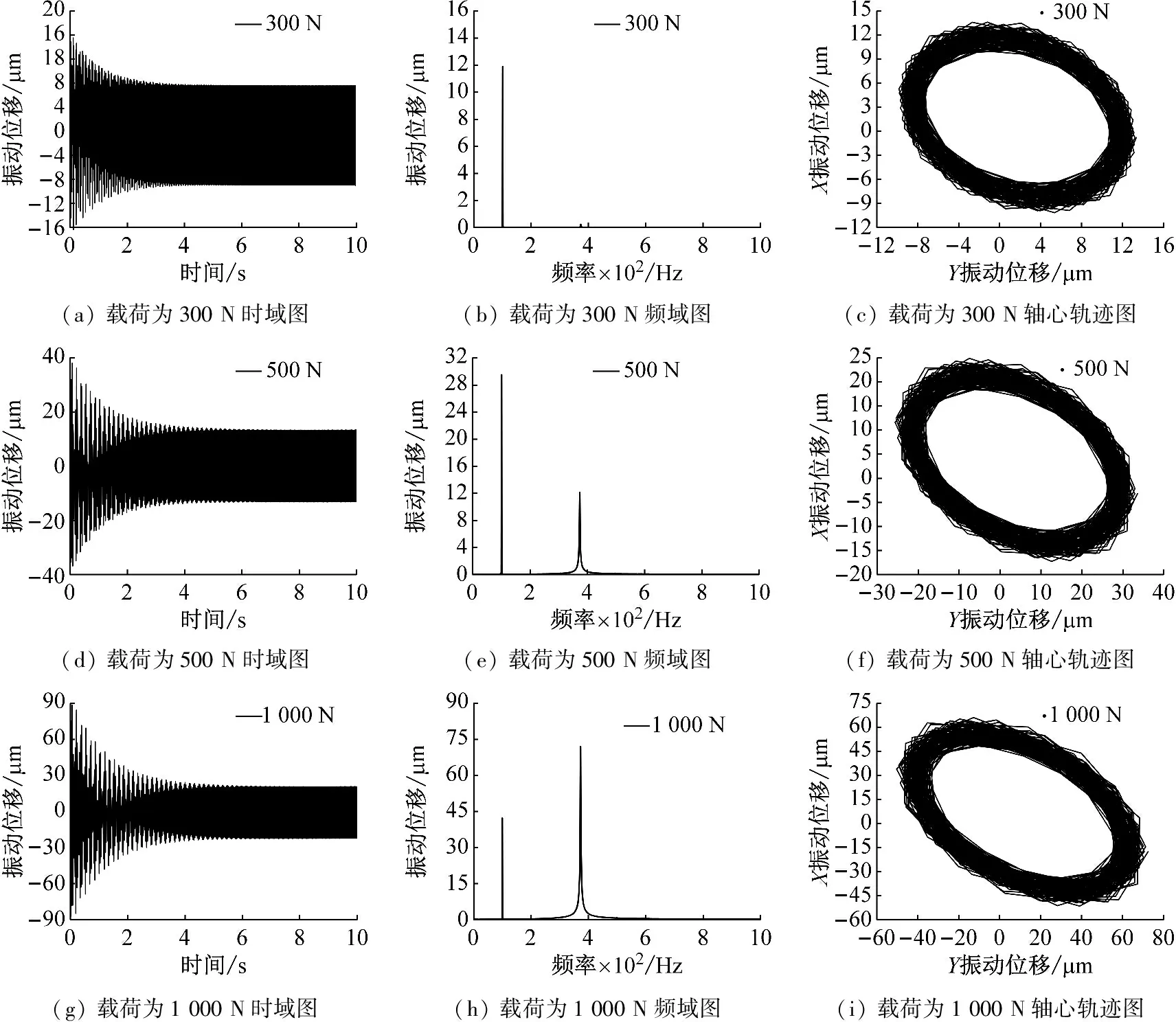
图10 不同径向载荷下的振动响应

通过模型计算所得的轴承振动数据进行分析,取0～10 s内的振动数据进行频域分析和轴心轨迹分析。由图10可知,随着载荷增加轴承振动频率成分并未发生变化,各频率对应的振幅值随着增大。因为随着载荷的增大轴承振动非线性递增,当轴承变形量达到极值后滚动体发生滑移,轴承整体振动呈现了减小的趋势。由轴承轴心轨迹图形可以看出径向载荷的增加没有对轨迹形状造成改变,但Z方向的位移量会随着载荷的增大而增加,进而导致轨迹图椭圆向长轴方向延伸。

4 周期性分析

本文研究的全陶瓷角接触球轴承系统为非线性系统,为了分析其周期性采用分岔图、相平面图和Poincare映射图来表述系统的响应情况。图11为本文提出的滑移接触理论下的轴承系统分岔图,图12为不同周期节点处的相平面图和Poincare映射图,可见转速在25 000 r/min前系统为五周期运动,25 000～60 000 r/min为十周期运动,60 000～200 000 r/min为拟周期运动。可见在考虑滚动体滑移运动的情况下系统周期性持续时间更久,仿真计算中所取转速范围内未发生混沌运动。

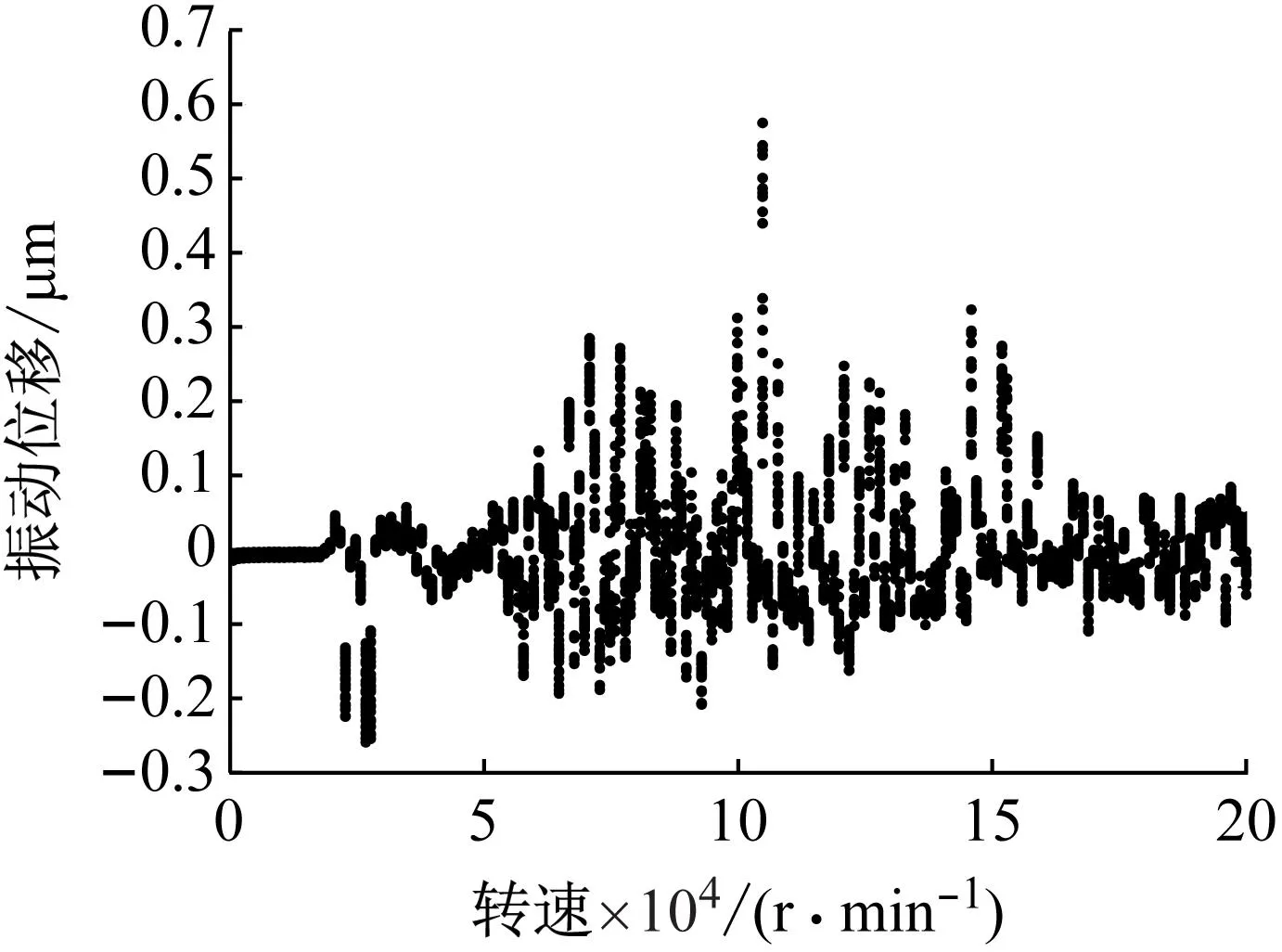
图11 滑移接触下的系统分岔图

图12 滑移接触下不同转速时的相平面图和Poincare映射图

5 轴承转子系统振动试验

为了验证本文所提出轴承动力学模型的准确性,搭建了如图13所示的轴承转子系统试验台。试验台为MFS-MG机械故障综合模拟试验台,由电机控制系统、回转系统和数据采集系统组成,通过压电式振动传感器采集轴承处的振动信号,经过数据采集装置处理后传送至电脑。试验中为模拟径向载荷为100 N的工况条件,选取20 kg的圆盘转轴作用于两个氧化锆陶瓷轴承上,单个轴承所受径向载荷为100 N,轴承尺寸参数如表2所示。

表2 轴承试验参数

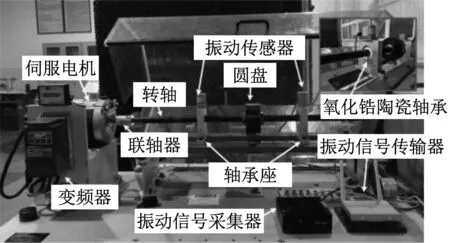
图13 试验平台

以转速3 000 r/min,径向载荷100 N为例,本文建立的轴承动力学模型振动位移计算结果与试验数据对比结果如图14(a)所示,时域分析图中计算的振动幅值为8.031 μm,试验数据得到的振动幅值为7.977 μm,两者平均误差为0.68%。频域图对比结果如图14(b)所示,图中的各峰值分别对应不同特征频率,其中一阶频率为50 Hz对应轴承的转动频率,二阶频率为100 Hz对应在承载区滚动体冲击时的振动频率,二阶频率的峰值对应轴承滑移现象的振动冲击值。由图14曲线可以看出,一阶和二阶频率与本文计算结果完全吻合,证明本文提出的考虑滚动体滑移下的轴承动力学模型具有很高的准确性。

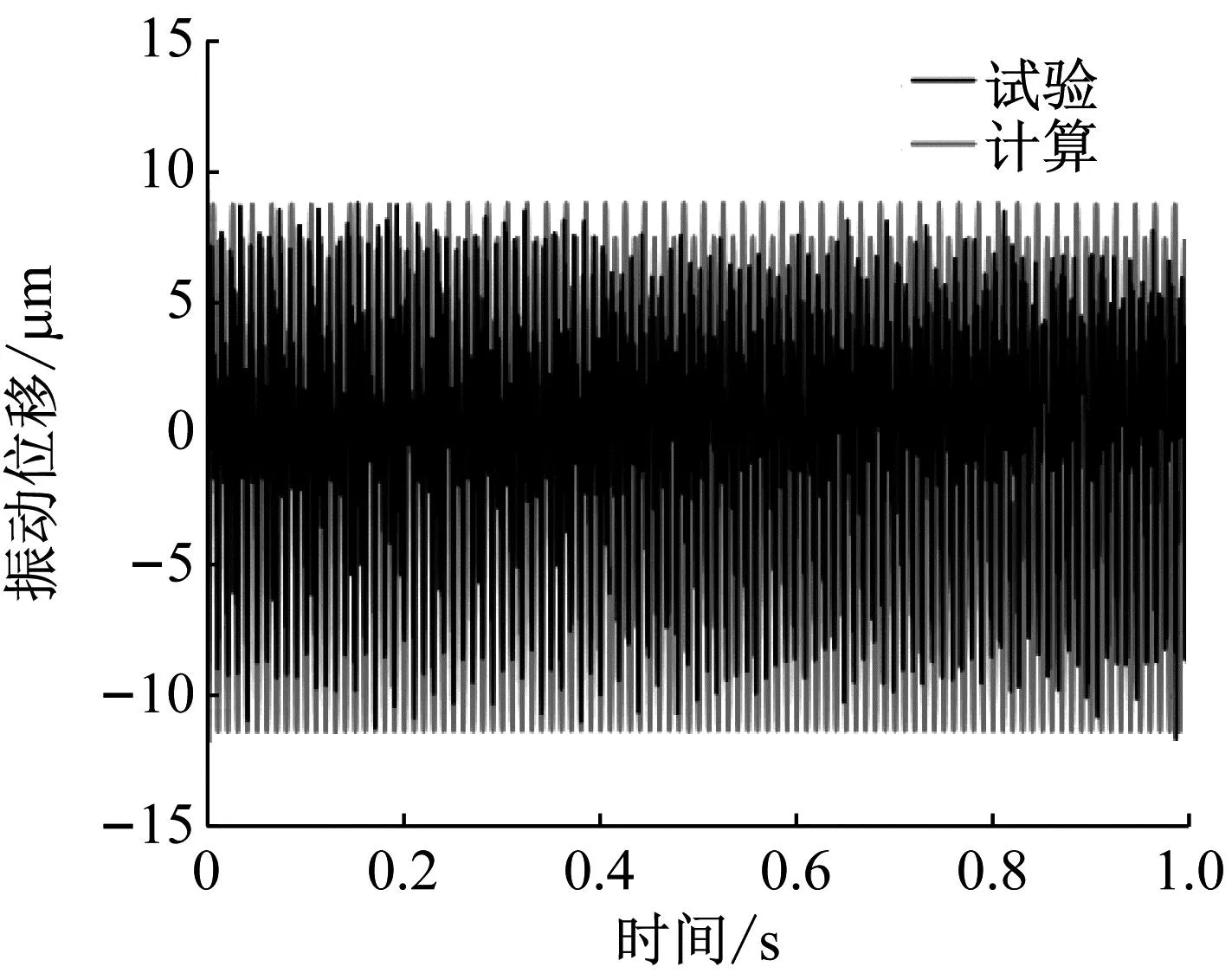
(a) 时域分析图

为了分析不同径向载荷发生滑移和正常接触时的振动特性,分别取径向载荷为100 N和200 N为例,计算不同转速下的振动位移幅值,并与试验台所测得的数据进行比较。不同工况下滑移接触与正常接触的对比曲线如图15所示。由图15可知,随载荷的增加,振动位移随之增大,但是增长率有所减小。随着转速的增加,振动位移随之增大,增长率呈现先增大后减小的趋势。在载荷为100 N时,滑移接触最明显的发生区间为4 000～5 000 r/min。在载荷为200 N,滑移接触最明显的发生区间为3 000～4 000 r/min。在同一转速和载荷条件下,正常接触的计算结果远大于试验数据,滑移接触计算结果与试验结果更加接近且略小于试验结果,考虑到试验中的客观扰动因素,采用滑移接触理论时得到的振动数据更加准确。

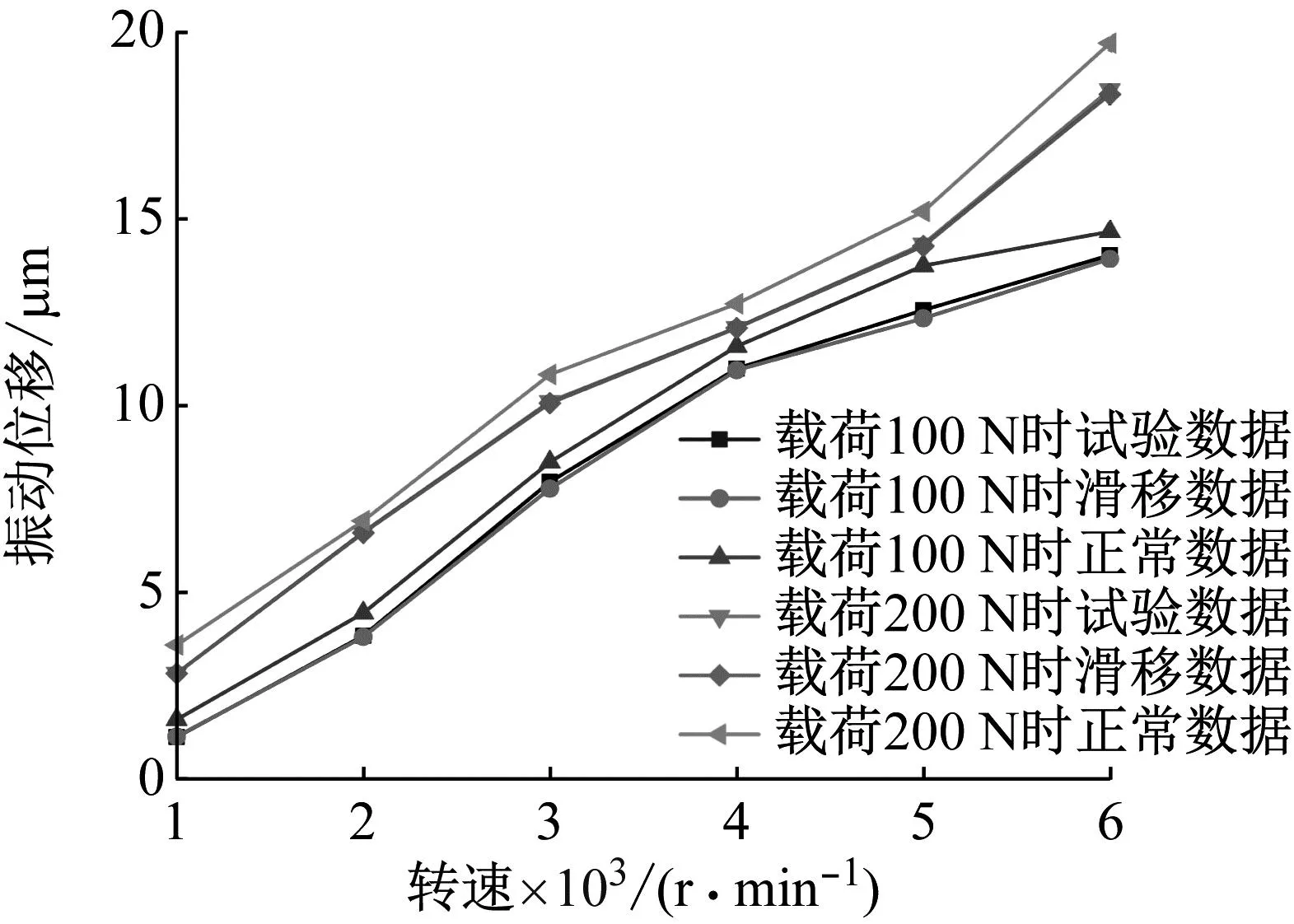
图15 不同载荷下滑移接触与正常接触对比

6 结 论

本文针对全陶瓷角接触球轴承滚动体滑移现象,建立了考虑滑移运动机理的轴承动力学模型,并运用本模型对轴承系统运动进行了振动仿真和周期性分析。最终得到主要结论如下:

(1) 通过接触力学的理论分析和计算,给出陶瓷滚动体滑移接触下的接触参数计算方法。通过滑移接触和正常接触时接触参数的计算结果对比,可见陶瓷滚动体的滑移导致接触参数有明显的变化。

(2) 对全陶瓷角接触球轴承动力学模型求解得到了轴承系统的振动规律,考虑滑移运动时模型计算的振动平均幅值与试验结果误差仅为0.68%,频谱成分与实际情况相同。证明本文建立的模型具有很高的准确性,能够很好地描述出轴承滑移特征下的振动情况。

(3) 通过混沌理论分析了本文建立的轴承模型的周期性和稳定性,可知考虑轴承滚动体滑移运动下的模型相比于传统模型更加具有稳定性,相比于常规接触情况的计算结果混沌运动有明显推迟。证明了本文建立的全陶瓷角接触球轴承动力学模型是非线性的,并且滚动体滑移接触对系统的影响是不可忽略的。