基于电容层析测量的油气两相流动态信号时频分析方法

徐一，李轶，马志扬，王海刚

（1 中国科学院工程热物理研究所，煤炭高效低碳利用全国重点实验室，北京 100190；2 中国科学院大学，北京 100190；3 清华大学深圳国际研究生院，广东 深圳 518055）

多相流动广泛存在于石油开采及油气混相输送管线中，其流动复杂性体现在各相非均匀混合且存在相互作用、流型变化复杂、特征参数多等特点。对这一非线性、高度随机性的瞬态变化过程实现实时在线的准确测量具有重要的理论意义和工程应用价值。近年来，研究者们致力于发展非侵入性、流型适应性强兼顾测量准确性、体积及成本的在线多相流量计，以期弥补依靠气液分离器和单相流量计的传统测量系统在实际工业应用中的时间延迟、维护困难等不足，从而适应油气开发的不同场景[1]。

电容层析成像（electrical capacitance tomography,ECT）通过重构感测截面的介电常数分布实现对非导电介质的可视化测量，且具有不产生压降、安全无辐射、响应速度快的优点，近年来被尝试应用于油气两相流动过程的实时监测[2-3]。然而，由于存在反演误差以及难以准确获得流体的真实数据，现有基于ECT 的成像方法难以有效提取多相流动态流动关键信息。层析成像的相关研究多以静态仿真和实验测量为主，缺乏动态数据信息，而基于数字孪生（digital twin, DT）技术辅助ECT成像的方法[4]有效拓展了现有研究手段，能够高效获取更加接近真实流场的动态测量数据。在数据分析方面，现有研究多侧重于优化ECT 的图像重建质量[5-6]，而对于原始电容信号内耦合的流场动态信息关注较少。在可视化基础上进一步提取层析测量信号中与多相流型和流动特性相关的特征信息，将有助于提升测量精度和对复杂多相流动机理的理解。

多相流测量信号是由表征不同流体动力学现象的多个分量共同作用的结果。常见的气液两相流压力信号概括反映了流速、相含率、湍流度以及气泡、液塞等不同尺度的局部和全局流动行为。应用不同的信号分析方法，主要包括时域、频域、时-频域和非线性分析[7]，可以从不同视角提取信号中蕴含的特征信息。小波变换是一种具有代表性的时-频域分析方法，能够在高频范围使用高时间分辨率、在低频范围使用高频率分辨率对信号展开灵活解析，适用于流态信息集中在低频段、以高度随机性的瞬态变化为特点的多相流动。Wang等[8]通过压力信号的连续小波分析有效提取了气固流态化过程中的流场局部特征。Nguyen等[9]对多通道阻抗空隙率计的测量信号应用连续小波分析，通过提取有效局部小波能量和有效尺度，建立水气垂直两相流的流型识别标准。李枫[10]基于电阻层析成像技术应用小波分析和人工神经网络模型，开发了针对气水两相水平管流的在线流型识别软件。陈飞和孙斌[11]通过多孔孔板测量，基于自适应线性调频小波对气液两相流的差压信号进行时频联合分析，并提取与流型变化相关的特征值。

针对动态研究中多相流动状态在时间、空间维度上均发生显著变化的复杂特性，以及由于感测信号中多信息融合难以通过单一变量或静态测试中有效提取流型特征的两方面难点，本文通过建立流电耦合仿真计算方法，获取更为接近真实多相流动过程的动态模拟测量数据，并对4种典型流型下的原始压力和电容模拟信号开展了多分辨率时频分析，从而有效解析流型变化与复杂测量信号特征分量的对应关系。连续小波变换实现了一维信号在时-频二维平面上的显示，有助于揭示流量波动和特征频率在时间上的变化规律。基于离散小波变换的多分辨率解析则将原始信号在相同的时间尺度上分解为多个不同频率尺度下的分量，获得各分量的能量占比，进而提取不同流型下的主导频率和能量分布变化。在流型的演化过程中，压力和电容测量信号的主导频率呈现一致的迁移规律，为流型转变的提供了有力判据。本文提出的信号分析方法在段塞流的实验测量中得到了检验，有效识别了段塞特征的细节变化。本文将ECT 测量的可视化图像与时频信号分析相结合，为精准多相流过程监测和计量提供了可靠依据和技术手段。

1 油气两相流动态测量过程仿真计算

1.1 流电耦合模型及计算平台构建

数字孪生通过构建多尺度、高保真的虚拟孪生体以及实际物理系统与虚拟空间之间的信息交互，从而准确获取单个部件乃至整个系统的动态信息，实现状态监测、性能诊断、行为预测和高效的数据分析[12]。本文基于前期研究中构建的流电耦合数值模拟方法[13]，通过耦合多相流动的计算流体力学（CFD）模型和ECT 的软测量模型，将多物理场同步计算下的流体力学参数和电学参数进行融合，从而实现传感器测量过程从物理空间向数字空间的精准映射。

多相流可以通过连续性方程和N-S方程来描述其质量和动量守恒，如式(1)、式(2)。

质量控制方程（连续性方程）

动量控制方程（N-S方程）

式中，Sm为源项；ρ为流体密度；u为速度矢量；p表示压力；μ为流体黏度；f为体积力矢量。

本文采用VOF模型[14]对多相流体进行求解，对于水平管气液两相流的典型流态可以获得较高精度的计算结果。

不同相被视作是共存且互相掺混的连续流体，通过引入相体积分数αq的概念来描述上述的守恒方程。采用固定网格的体积追踪方法以模拟气液界面，并重构相应的流场参数，例如n个组分构成的多相流体的密度可表示为式(3)。

ECT 测量对应静电场的控制方程为简化的Maxwell方程，如式(4)。

式中，ε为介电常数；φ为电势；Q̇为电荷量。

在现有的ECT 成像算法中，线性反投影（linear back-projection, LBP）算法原理最为简单，且计算速度快[15]。考虑到成像的实时性和对不同流型的适应性，经过初步算法对比测试确保成像质量在可接受范围内，本文统一采用LBP算法进行图像重构，根据测量得到的归一化电容向量λ和灵敏度矩阵S，反演出灰度值分布矩阵g，如式(5)。

依据上述气液多相流和ECT 的物理方程，两者耦合的关键在于重构流场中的介电常数分布。与式(3)类似地，在VOF 模型下建立多相流体的介电常数ε与相体积分数αq之间的数学关系，如式(6)。

由此将多相流场计算结果转换为Maxwell方程求解的条件，从而实现多相流场与静电场的同步计算。

基于上述流电耦合模型，本文借助Fluent 19.2、COMSOL Multiphysics 5.4 和MATLAB R2018b 多 平台协同，实现了动态测量仿真计算。Fluent软件中基于VOF 模型求解多相流控制方程，并借助用户自定义函数（user defined function, UDF）重构感测区域内的介电常数分布。COMSOL软件中根据介电常数分布求解静电场方程以模拟ECT 的测量过程，从而获得每一次测量的独立电容值。MATLAB软件中借助LBP算法根据独立电容值进行图像重建，同时实现多相流场与静电场之间的数据交互。通过对比流场计算结果与重构图像可以验证计算模型和架构的有效性，并对仿真测量进行质量评估。

1.2 几何模型、网格及工况设置

图1中显示了本文数值模拟中构建的几何模型以及对应的网格结构，包括12m 长、内径为50mm的水平圆管和位于距管道入口10m处的八电极ECT传感器，ECT 传感器的单个电极径向角为37.5°。流场模拟中的三维网格共有817718 个单元，静电场模拟中的二维截面包括1194 个网格，均经过事先验证以确保网格的独立性和仿真精度。依据实验室测试结果设置了表1中的油、气两相物性参数设置，其中气相为空气，油相为实验室常用的白油。

表1 仿真计算物性参数设置

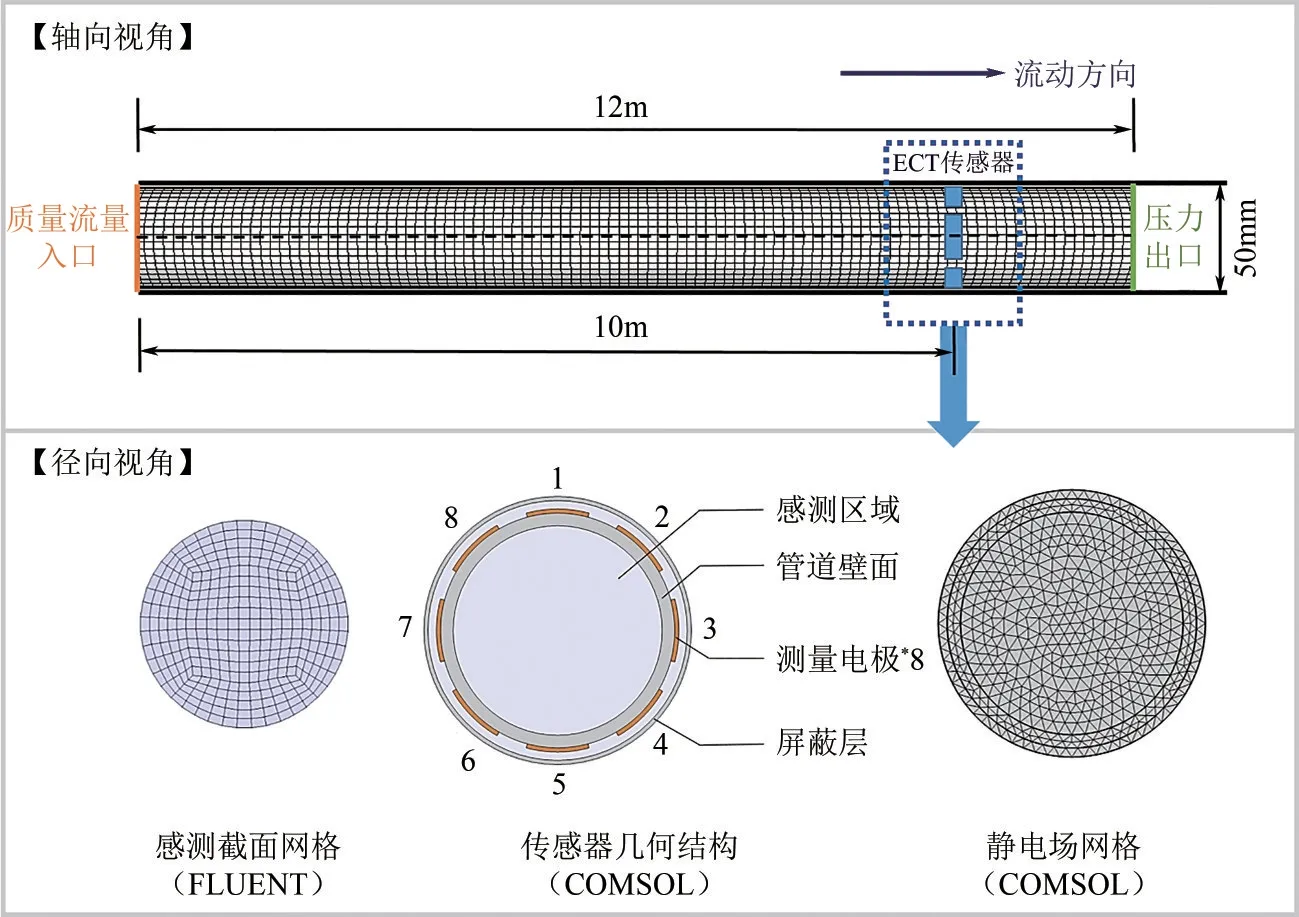
图1 几何模型及网格结构

经验流型图是长期以来多相流动研究中的常用手段之一。鉴于表1中的物性参数的适用范围，使用Mandhane 流型图[16]参照选取了表2 中的模拟工况，初步计算后在水平管内形成了相应的4种典型流态，即波浪流、气团流、段塞流和泡状流。

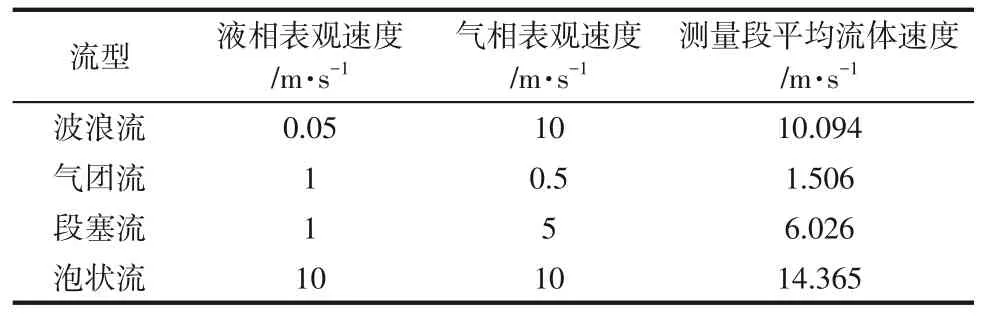
表2 仿真计算进口条件及多相流体速度计算结果

1.3 计算结果及初步分析

参考压力信号，本文以电容平均值μc作为特征参数，将ECT 原始测量数据转化为一维时间序列信号以便分析。由于采用八电极传感器和单电极激励方式，每次测量可获得C28= 28 个独立电容值，故μc计算公式如式(7)。

4种模拟流型下的压力、电容原始信号以及相应的ECT 成像如图2 所示，由于压力变化范围较大，为便于观察，压力信号的纵坐标选用了对数坐标。ECT图像包括基于LBP算法生成的瞬时横截面图像以及管道轴向的流态重建图像，轴向图像是通过多帧横截面图像按时间顺序堆叠而成的，能够更加清晰地将管道内部的多相流场进行可视化表达。所有测试流型下的ECT 成像精度均已经过事先测试，ECT图像与Fluent流场计算结果得到的流态始终保持一致。基于ECT成像得到的4种流型下截面空隙率的时变规律也与流场计算结果一致，平均相对误差依次为3.62%、1.93%、5.47%和18.60%。

图2 不同流型下的仿真测量信号及ECT重构图像

结合并对比ECT的反演图像和测量信号，4种流型及其测量信号主要有以下特征规律。

（1）波浪流持液率较低且流动状态相对稳定，压力值和电容值明显低于其他三种流型，但测量信号均能灵敏感知其液位变化。

（2）气团流的液相流量显著增加，持液率较高，气流吹起液波幅度会间歇性达到管顶，阻塞气体流通面积，形成液塞和气团交替出现的流动状态。电容和压力信号均较波浪流有显著提升，并呈现出类似于周期性的变化规律。ECT图像能够感知气团的出现，并准确还原气团的形态。

（3）段塞流与气团流类似，但通常具有更高气相速度，导致相对较低的段塞频率，以及更加剧烈的两相间相互作用因而形成的不规则油气界面。压力和电容信号均能反映出段塞频率和液塞形态的相应变化，且压力信号在更高流速下表现出了更加宽范围的周期振荡。ECT的重构图像依然可以较为敏感地还原液塞和气团的形态特征。

（4）泡状流的液相流量进一步提升，液体的湍流脉动破碎管道顶部的气团，使其变为小气泡分散于液相上层。ECT图像能够很好反映管道顶部以气相为主、下部以大量液相为主的两相分布规律。由于其高流体速度和高液相含率，压力和电容信号值明显高于其他三种流型，但变化较为平稳。

此外，根据测量原理及计算结果可知，压力信号值与相含率、流速以及湍流度等多因素均相关，而电容信号值仅与相含率和气液横截面分布相关。尽管测量信号的时间序列波动和ECT 重构图像能够反映基本的流态结构和变化规律，但无法解析出耦合在原始信号中的各项流动参数和流场信息，亦无法定量分析以建立更加明确的流态判据，需要进一步应用先进信号分析方法对其进行深入探究。

2 测量信号的多分辨率时频分析

2.1 连续小波变换

现实中的测量信号通常是非平稳信号。常见的傅里叶变换被广泛应用于解析信号中出现的频率分量[17]，但其无法提供不同频率发生的时间定位。故在此基础上发展出了短时傅里叶变换（short-time Fourier transform, STFT）[18]，将信号拆分成不同单元，从而获取信号的局部特征。然而，STFT 中的窗口大小在整个计算过程中是固定的[图3(a)]，时间分辨率和频率分辨率不能两者兼顾。连续小波变换（continuous wavelet transform, CWT）[7]则克服了STFT 中的固有分辨率问题[图3(b)]，在高频区域使用高时间分辨率，在低频段则使用高频率分辨率，这将能适应现实中很多信号在长时间内具有缓慢振荡、在高频则多以瞬态突变居多的物理特性。

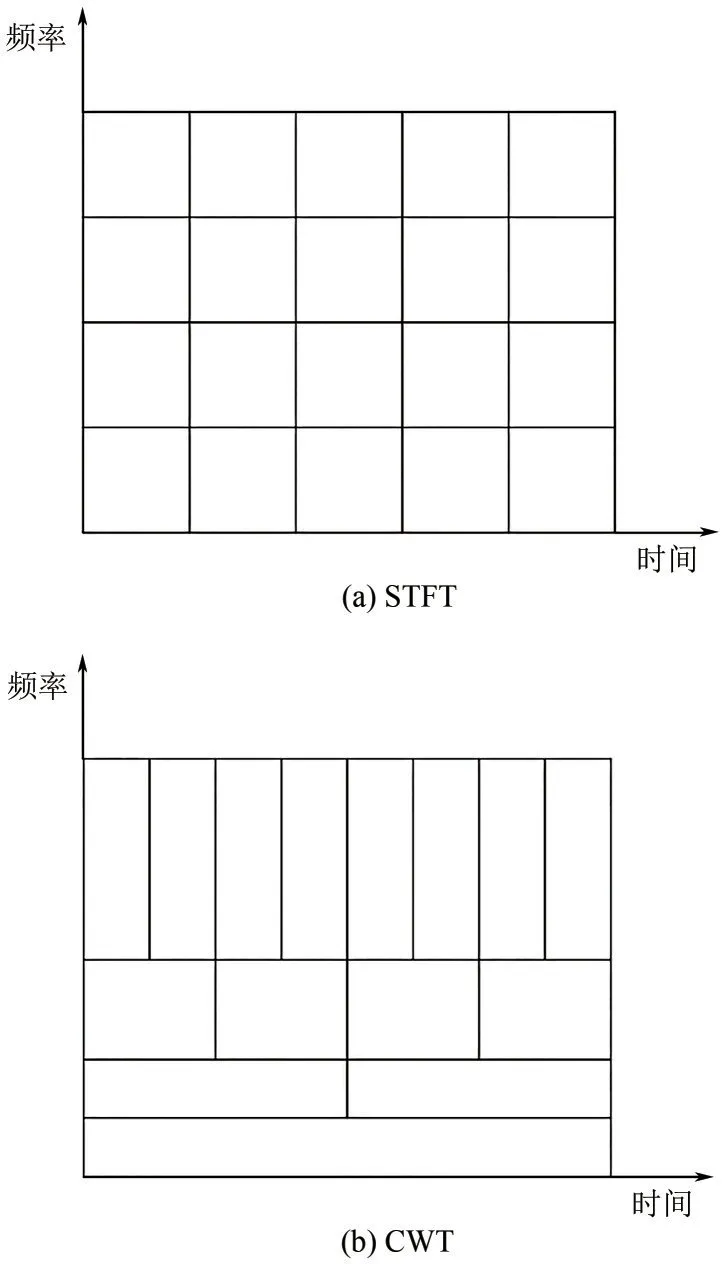
图3 短时傅里叶变换和连续小波变换的时频拆分特性

信号f在尺度s下的连续小波变换公式由式(8)表示[9]。

式中，ψ为小波基函数；上角标*表示复共轭；通过调节尺度s和位移τ的大小来改变基本小波的形状以获得不同时频尺度下的信息。

连续小波变换公式也可写为式(9)的内积形式，表明小波变换系数C(s,τ)是原函数与小波基函数相似性的度量。图4中显示了取绝对值后不同流型下基于式(8)生成的CWT系数图。

图4 不同流型下的CWT系数图

不同流型下的测量信号CWT 结果呈现出鲜明的特征差异。

（1）波浪流以中低频段、长时间稳定的小幅震荡为主，CWT 图像可以清晰反映液位变化的剧烈程度，并定位其出现的时间。在0.5～1s 的时间段中，系数绝对值明显增大，且伴有高频响应，表明此时的液位变化较其他时段更为剧烈。

（2）对于气团流和段塞流这两种间歇流型，系数较大的部分仍分布在较低频段，并在液塞通过的时间区域内有显著响应，且段塞流的液塞频率更低但能量更为集中。

（3）泡状流的波动则主要集中在高频段，反映了以气泡行为为主导的流态特征。与波浪流类似，电容信号的小波变换系数整体偏低，表明气液比随时间变化很小，流态相对稳定。但压力信号受高流体速度的影响，系数较波浪流显著升高。

在模拟的4种流型下，小波变换系数的时频分布在压力和电容信号上都呈现出一致的规律性，且对于气液结构的瞬态变化能够提供准确的时间定位。能量集中的频率范围会随流型变化而产生显著差异，这意味着对原始信号进行频段分解可能有助于解析不同流型特征在测量信号上的相关表征，从而建立更为量化的流型判据。

2.2 小波多分辨率分析

信号通常由多个具有物理意义的分量构成。多分辨率分析方法（multi-resolution analysis, MRA）将信号可逆地分解为不同频段上的多个分量，从而能够在与原始信号一致的时间尺度上单独研究每一个分量的变化，常用方法包括小波多分辨率分析[19]、经验模态分解（empirical mode decomposition, EMD）[20]、变分模态分解（variational mode decomposition,VMD）[21]等。小波MRA 通过小波的固定函数来分离信号，对于在较低频率上分离多个频率接近的振荡分量以及捕捉数据中的瞬态变化通常有较好的效果。参考连续小波变换分析结果，表征多相流型变化的信号通常集中于较低频率，压力信号响应多集中在30Hz 以内，电容信号大多在10Hz 以内。同时，对于间歇流，液塞出现对应的信号突变是研究中关注的重点之一。因此，小波MRA 方法在原理及特性上适用于本文研究中的多相流动信号分析。

信号f对于小波函数Ψ和尺度函数φ的小波级数展开定义为式(10)。

式中，c和d分别为近似系数和细节系数。

由式(10)的计算原理可知，若令初始尺度j0=0，原始信号f经过有限N层小波分解之后会获得N个由小波函数产生的高频“细节”组分（detail,D）和1个由尺度函数产生的低频“近似”组分（approximation,A）。本文中对原始测量信号进行了6 层小波分解，Dk层的频率范围应为为采样时间间隔。压力信号的采集速度统一设置为100Hz，电容信号则为50Hz。表3中列出了分解后不同频段的频率范围，并统一定义了本章后续分析中的高频、中频、低频所指代的频段。

表3 压力和电容信号在多分辨率分析中的频段划分

不同流型下压力和电容信号的多分辨率分析结果如图5所示，每幅子图中均包含6个“细节”组分和1个“近似”组分，随着频率从上至下逐渐降低，组分信号变得越来越平滑。图中分别用蓝、灰底色标记出了构成信号最主要和次主要的频率分量，最主要频率分量随流型变化的迁移规律在压力和电容信号的分解中展现出了令人满意的一致性。当流型从波浪流到间歇流再到泡状流的变化过程中，主导频率先由中频段转向低频段再转至高频段，这分别对应了波状流中的中等频率液面波动、间歇流中的低频液塞以及泡状流中的高频气泡行为。由于压力和电容参数的影响因素和所表征的流动信息不同，信号分解结果在次主要频段的分布上呈现出细节差异。例如波浪流下压力信号的次主要分量位于比主分量更低的两个中低频段，而其电容信号的次主要分量则分别位于较主分量一高一低的两个分量。较低频率的分量反映了波浪流全局上的稳定流动，而中频段则对应了气流吹拂下的液位波动。在两相物性不变的条件下，由于电容值仅与相含率和两相分布相关，对于液位波动会更加敏感。

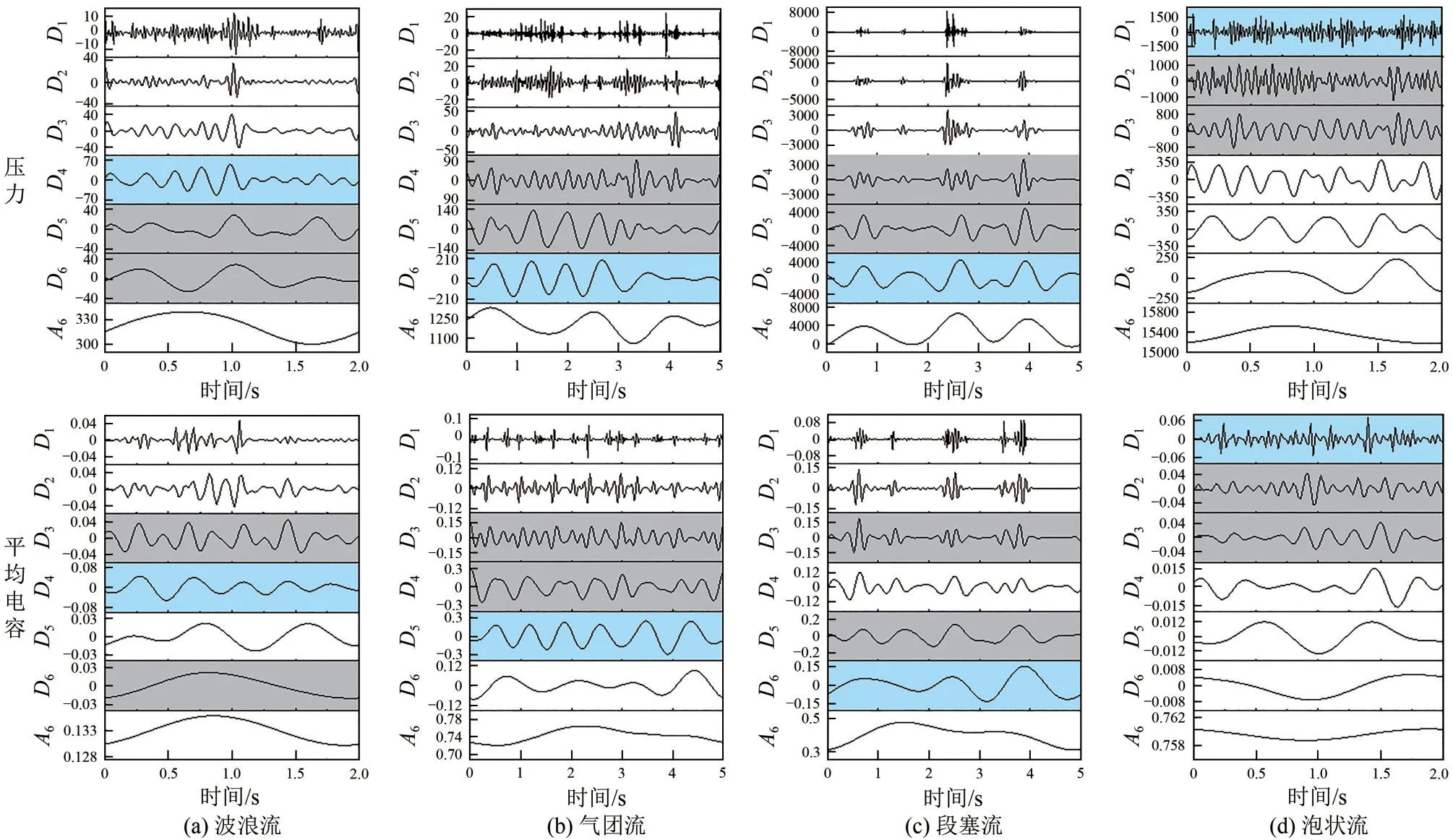
图5 不同流型下的小波多分辨率信号分析

为了更加直观量化地观察各频率分量，定义各组分的信号能量为该组分小波分解系数的平方和，并根据式(11)计算第L层细节组分在所有细节项中的能量占比。

式中，k为小波分解系数数量。

图6中显示了各频段的小波能量比，进一步佐证了上述频率迁移规律，并使得各频段的能量分布差异更为直观。而在后续实验分析中，能量分布图还将表现出在同一流型下展现不同流动细节的能力。

图6 各频段小波能量分布

3 动态实验测量

在模拟测量信号分析的基础上，进一步对段塞流的ECT 实验测量信号展开多分辨率时频分析，以验证上述数据分析方法和模拟结论的可靠性，并着重分析在同种流型下小波分析方法对于流场细节变化的提取能力。

3.1 多相流实验平台

图7中显示了多相流实验平台的示意图，不同的流体工质从各自的储罐流出，混合后在测试管段形成气液多相流，应用ECT 传感器进行测量后分离回到各自储罐，从而进行循环流动。鉴于本文的研究对象，仅使用油路和气路进行实验，且两相物性参数与表1中仿真计算的设置一致，进口流量通过流量调节阀进行调节以形成不同的两相流动状态。实验管道的横截面结构也与仿真计算的几何模型相同，均为内径50mm的水平圆管。ECT传感器为八电极结构，电极径向角为31°。参考仿真计算结果，电容信号中表征流型变化的响应大多集中于10Hz 以内。综合考虑信号分析的有效性、实验室传感器的采集能力和长时间测量的数据量，实验测量中的数据采集频率选取20Hz。

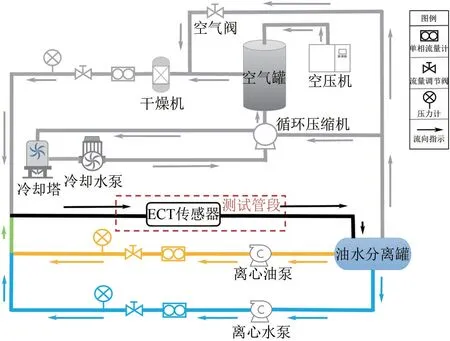
图7 多相流实验平台示意图

3.2 段塞流过程监测及信号分析

实验在30m3/h的恒定气相流量下进行，通过在0.5～2.5m3/h范围内调节油相流量，在被测管段形成不同的段塞流形态。每一测试工况下取稳定运行后60s 内的测量信号进行分析，为便于观察，表4 中对比了0～20s 内的ECT 图像与小波变换结果。由ECT轴向重建图像可知，随着液相流量的增长，液塞呈现出先变长而后变短促的特征规律。这一特征变化在连续小波变换结果中表现为整体持液率提升导致的低频段响应逐渐增强，以及液位波动频率先变缓后加剧导致的较高频段振荡先减弱后增强。与2.1节中的仿真结果进行比对，CWT 的分析结果在流型基本特征的反映上具有一致性，在0～10Hz 的频率范围内能够明显捕捉段塞流的间歇振荡并提供时间定位。但实验信号整体上的时频特性会更加复杂，尤其当观测的时间尺度显著增长时，仅从CWT 变换结果中直接辨别出流场细节的特征变化更为困难。

为了进一步清晰展现流型和流场细节变化对测量信号的影响，对电容信号进行小波多分辨率分析。由于均为段塞流状态，不同液相流量下各信号分量的整体波动规律接近，故选择图8中更加简洁和便于量化观察的能量分布图进行分析。由图可知，低频段D5始终为主导频段，对应实际频率范围为0.31～1.25Hz，与第2 节中数值模拟的段塞流主频范围（0.39～1.56Hz）基本一致。而随着液相流量增加，高频段D1的能量比重明显回落，而低频段D4、D5的主导优势变得更加明显。进一步观察主频段D5，液相流量由0.5m3/h 提升至1.5m3/h 的过程中，能量占比明显增加，这反映了稳定段塞频率下液塞长度显著增加。而液相流量继续增加到2.5m3/h的过程中，D5的能量占比有所下降，而D3、D4的能量有所提升，这反映了液塞长度变短且段塞频率增长的趋势。

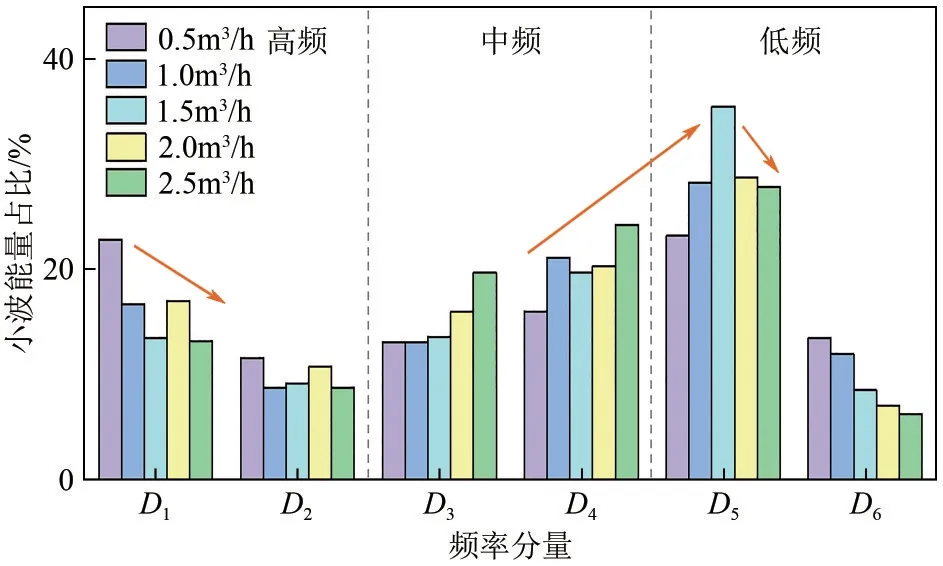
图8 不同油相流量下的小波能量分布

通过动态实验测量和上述相关数据分析，本文应用的信号时频分析方法在实际测量中可以有效揭示流动状态和气液结构特征。作为流型的主要判据，实验测量信号的主频范围与仿真计算结果一致，验证了数值计算模型和流型判断依据的有效性。连续小波变换结果能够有效定位频率变化出现的时间，这对于段塞流这类瞬时变化剧烈的间歇流的过程状态监测能够起到重要作用。而小波多分辨率分析结果一方面可以在低频段提供较高的频率分辨率，从而有效通过主导频段确定流型；另一方面通过分析能量迁移规律，能够简洁快速地获取气液两相结构的细节变化。将基于小波的多分辨率时频分析与常规的ECT 可视化图像相结合，可以仅在电容测量的单一模态下同时为管内多相流流动状态提供定性和定量的特征描述，有效拓展了电容数据在多相流测量上的表征作用，从而为实时在线监测和过程控制提供更加丰富的多维信息。

4 结论及展望

基于流电耦合仿真和多相流实验对油气两相流过程进行动态监测，并基于小波时频分析方法将原始时间序列信号在时间域和频率域上同步解析，在流动可视化的基础上进一步挖掘了测量信号中蕴含的流场特征信息。主要研究结论如下。

（1）连续小波变换能够有效提取油气两相流动中长时间的低频波动和瞬态的高频突变，并给予时间定位和强度表征。

（2）小波的多分辨率分析从频率角度提供了不同流型的量化判据，当两相流动在“波浪流—间歇流—泡状流”的演化过程中，主频带相应呈现出“中频段—低频段—高频段”的迁移规律。

（3）不同频段上的小波能量分布变化能够简明反映气液两相结构的动态变化，在确定主导频率的基础上，有效识别段塞频率和液塞形态的变化规律。

在本文研究的基础上，可进一步开展以下工作。

（1）在仿真计算以及实验、工业环境的实际测量中拓展数据集测试范围，以适应不同流体的物性差异和多变的实测环境因素。

（2）借助连续小波变换的时间定位能力，修正现有的流量计算模型，以提高计算模型的适应性和准确性。

（3）将ECT 图像和测量信号的时频特征分量共同作为模式识别的有效输入，提升流型判别模型的准确性和可解释性，进而优化不同流型下图像重建效果和关键参数的计量精度。

符号说明

A—— 小波多分辨率分解后的近似组分

C—— 小波变换系数

c—— 近似系数

D—— 小波多分辨率分解后的细节组分

d—— 细节系数

f—— 体积力矢量，N

g—— ECT反演图像的灰度值分布矩阵

p—— 压力，Pa

Q—— 电荷量，C

S—— ECT灵敏度矩阵

Sm—— 源项

s—— 小波函数尺度

u—— 速度矢量，m/s

αq—— 相体积分数

ε—— 介电常数，F/m

λ—— 归一化电容向量，F

μ—— 黏度，Pa·s

μc—— 电容平均值，F

ρ—— 密度，kg/m3

τ—— 小波函数位移

φ—— 尺度函数

Ψ—— 小波函数

ψ—— 小波基函数