管内相分隔状态下湿气两相流双参数测量方法

边汉青，张兴凯，廖锐全，王栋，李锐，罗晓矗，侯耀东，白晓弘，甘庆明

（1 油气钻采工程湖北省重点实验室(长江大学)，湖北 武汉 430010；2 西安交通大学动力工程多相流国家重点实验室，陕西 西安 710049；3 长庆油田分公司油气工艺技术研究院，陕西 西安 710021）

我国天然气储量、产量逐年上升，成为了我国主要的能源消费类型之一，作为低碳的化石能源为2030 年前碳达峰提供了巨大的贡献，预示着未来行业发展的可持续性[1-2]。自初投入开发以来，天然气计量研究属于气液两相流的范畴，目前多采用分离计量法或者不分离在线测量法作为气藏、气井的主要计量方式。在气举井、输气管道以及产气井中的天然气，其都可能含有一定量的液相组分，一般把这种地面生产系统中的天然气与游离水、液态烃等组分的混合物称为“湿气”[3]，而油气集输中的“湿气”的定义：“在气藏条件下没有液相，但在地面条件下气体内出现液烃”，在一些气井及气举井中高气液比的天然气也可叫作湿气。对于湿气的定义，现今仍没有统一的标准，仪表测量按照据美国石油学会（API）[4]及《用安装在圆形截面管道中的差压装置测量湿气体流量》（GB/Z 335588—2017）[5]对湿气的定义：“气液两相流的体积含气率大于95%即为湿气”。湿气是气液两相流的一种特殊形态，相对于单相流动而言，湿气存在气液之间的速度滑移，同时其流态受时间、操作压力以及温度的影响较大。湿天然气中液相组分的存在使得气相流量测量结果虚高，这将极大地增加湿气计量的难度与成本，因此亟需一种简单便捷、高精度的在线测量方法。

由于差压式流量计结构简单、测量重复性好且造价低廉，在气液两相流测量当中输出稳定，因此广泛应用于湿气的流量计量当中。其中文丘里管具有测量精度高、抗压能力强、结构比较简单、应用范围广泛等优点。它是基于流体动力学原理设计的，通过对收敛截面的几何参数进行设计，可以使得扩散截面处的压力差与流量成正比，从而实现对流量的测量。此外，在文丘里管测量中需要考虑流体的物理特性（如密度、黏度等）、文丘里管的几何参数（如收敛角度、入口直径等）及其安装环境等因素，因此需要配合相应的计算方法和校准系统进行使用。同时在油气田中，出口和输送管线中的液相含量会影响相应能源的计量和质量分析，这便是差压式流量计进行湿气测量时产生的虚高现象。国内外针对这种虚高现象通过文丘里管进行了大量的实验与模拟，并建立了一系列的修正模型，其中使用最为常见的模型为林宗虎模型[6]、改进的Murdock模型[7]、De Leeuw模型[8]、Steven模型[9]以及ISO 模型[10]等。湿气流量计还需要能准确测量液相的含量和流量，从而确保能源计量的准确性和合规性。但由于湿气中存在液相水，因此会对湿气测量产生极大的误差。

目前双压差测量法广泛应用于两相流测量的研究。2013 年，He 等[11]提出了一种基于文丘里管的双差压法测量含水率，通过理论分析阐述了双压差法的原理，为验证双差压法的可行性，进行了低压湿气试验。2021 年，Zheng 等[12]提出了一种由旋流器和长喉文丘里管组成的测量装置，通过旋流器将流型转化为环状流可以提高测量精度，减少湿气中含有少量液体时造成的误差，同时采用轴向、径向双压差进行湿气测量。从2012 年至今，多相流管内相分隔理论和方法已经用于气液两相流体流量测量[13-14]，同时将管内相分隔技术与双压差测量法相结合表明测量结果较好。2020年，王帅等[15]开发了一种基于相分隔的油水两相流测量方法。通过旋流器实现相分隔，将油相集中到管道中心使进口流型变为环状流，利用轴向、径向双压差来联立求解质量流量及含液率。次年，杨杨等[16]同样基于管内相分隔技术对高含水油水两相流进行了测量。2022 年，雷玲卷等[17]以甲烷-水为介质进行了数值模拟研究，建立了基于双压差特性的湿气流量测量修正模型，有效减少了液相水对测量结果的影响。但由于其只进行了数值模拟研究，对于实际工况下适用性可待考究。由以上文献调研可知，双压差测量法在研究湿气通过文丘里管时具有较好的可行性。但这些研究仍处于室内实验阶段，其实验压力多是低压，达不到气井和气举井高压的条件；并且对于油气田现场的应用较为少，其对现场试验的测量性能缺少定性的评估。因此，需要针对基于相分隔的湿气双参数测量法开展高压实验验证其适用性，这也是未来湿气测量的发展趋势。

上述的这些研究为湿气测量提供重要理论基础，本文通过在文丘里管前端增加叶片式旋流器以减少流型对实验的误差，在前期探索基础上使用轴向压差、径向压差双参数进行高压工况下湿气气相、液相质量流量的测量，得出基于管内相分隔法的湿气双参数测量模型并用于中石油TH 油田现场试验。

1 装置及原理

1.1 物理模型

物理模型由旋流器+文丘里管组成，采用叶片式旋流器来实现多相流的管内相分隔，旋流器的旋流叶片由4 个呈45°倾斜的半椭圆片组成。物理模型结构见图1所示。

图1 物理模型结构示意图

测量装置共设置3个取压，分别为：文丘里管进口中心取压p1、文丘里管进口管壁取压p2以及文丘里管喉部管壁取压p3。文丘里轴向压差与相分隔径向压差用于联合测量湿气，Δpr和Δpa如式(1)、式(2)所示。

1.2 双参数测量原理

1.2.1 轴向压差原理

传统的流动文丘里喷管结构分为入口段、入口收缩段、喉部和出口扩散段等几个部分。湿气的质量流量与轴向压差的关系如式(3)所示。

式中，C为流出系数；β为直径比，d/D；Δpa为壁面轴向压降，Pa；ε为膨胀系数。

真实流量由虚高修正系数Φ得到，如式(4)。同时虚高修正系数Φ取决于气液密度比、Lockhart-Martinelli 参数XL-M和气体弗劳德数Frg，如式(5)、式(6)和式(7)所示。

式中，g是重力加速度，m/s2；ql和qg分别为液相和气相的质量流量，kg/s；ρl和ρg分别为液相和气相密度，kg/m3；x是湿天然气干度；D为管道进口直径，m。

现有的模型大多是测量气液两相流中气相流体质量流量，并在基础上进行修正虚高，但实际现场环境难于获取L-M 数、气体Froude 数，因此本文采用经验公式计算的方式来获取气相质量流量，避免了气相的虚高。由于管道直径、气液密度是已知条件，根据上述函数关系将轴向压差转化为质量流量和虚高系数的方程，可表示为式(8)，又可表示为质量流量、气液密度比跟干度的函数如式(9)。

1.2.2 径向压差原理

与上述单相流校正方程不同的是，通过多相流的相分隔技术，理想状态下可以实现管内各相之间独立而完整的界面，各相在管内占据特定的连续空间，两相之间有相对规则而清晰的分离界面，最终形成管内平稳平行流动的单相流体，有利于提高测量精度[18]。王帅等[19-20]在研究管内相分隔压差特性的基础上，分别得到了基于轴向压差、径向压差的油水两相流质量流量计算方程，利用方程关联求解质量流量。

因此，见图2所示在管道的一个横截面上，管壁与管道中心之间的径向压差Δpr可以认为是气相从管道中心到气液界面的径向压差Δprg与液相从气液界面到管壁的径向压差Δprl之和。关系如式(10)所示。

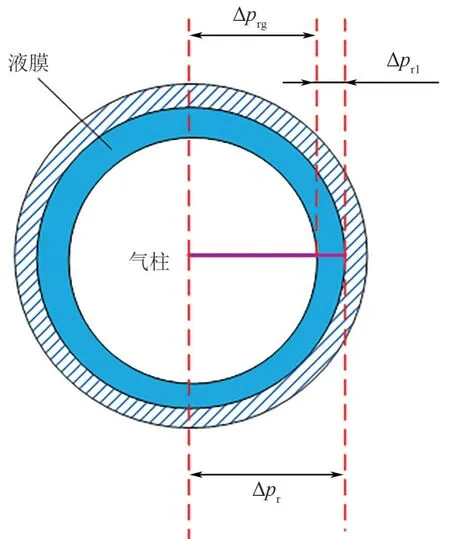
图2 管内相分隔径向压差理论示意图

式中，Δprg可以看作是气相单独流过直径为d的假想管道时的径向压差，Pa；Δprl可以看作是液相单独流过环径差为(D-d)的假想管道时的径向压差，Pa。

根据管内相分隔机理研究[21]，当单相流体流过时气体质量流量可表示为式(11)。同时，ql可以表示为式(12)。

式中，α是流量系数，通过实验标定。

引入新的压差，即从管道中心到管壁的径向压差Δprl1，表示质量流量一定且流体介质均为单相水时ql又可以定义为式(13)。

再次引入新的压差Δprl2表示当流体介质均为单相水时管径为d（气柱直径）的从管道中心到管壁的径向压差。假设这部分水的质量流量ql等于气相的质量流量，且流量系数也相等，则两者的关系为式(14)。

因此Δprl2也可以表示为式(15)。

理论上Δprl可以用Δprl1和Δprl2的差值来评价，可以表示为式(16)。

则径向压差可表示为质量流量、气液密度比跟干度的函数，如式(17)。

因此将轴向压差、径向压差的推导公式相结合可以得到双参数测量的模型，表示为式(18)。

由式(18)可以看出压差比取决于气液质量流量、密度、干度的关系，由于考虑到不同井实际气体密度不同，因此虚高模型也可以表征为压差比K、气液密度比ρg/ρl、压力P、温度T和气相弗劳德数Frg的函数；而气液质量流量比可以表征为压差比K、压力P、温度T和气相弗劳德数Frg的函数，见式(19)、式(20)。

2 基于管内相分隔法的双参数测量模型建立

2.1 网格划分及边界条件

本文采用ANSYS Meshing软件对模型抽出的流体域区域进行网格划分，中部有结构较为复杂的旋流器，在旋流器段以及取压口段采用非结构化网格，并进行局部加密，而在流体域其他区域则采用结构化网格进行划分，进行了网格无关性验证其最佳网格数为83.3 万，网格无关性验证见图3 所示。模型整体网格划分情况见图4所示。

图3 网格无关性验证

图4 网格划分

方程求解设置为SIMPLE 算法，涉及气液相压力变化多相流模型选用Eulerian 模型[22]。根据Wang 等[21]的研究，湍流模型选用对复杂流动能进行准确预测的雷诺应力模型（RSM）。压力项设置为一阶迎风格式，管道壁面边界条件为无滑移壁面。入口边界条件为质量入口，出口边界条件为压力出口，主相为甲烷，第二相为水。模拟工况条件：压力为2～10MPa；总质量流量为1～6t/h；干度为0.4～1.0（不同压力下对应体积含液率0～3.20%、 0～6.29%、 0～8.80%、 0～11.68%、 0～14.61%）；对应压力下气液密度比为0.022～0.114；温度为303.15K。由图5 可知，在Mandhane 流型图[23]中入口工况流型主要为弹状流、波状分层流和环状流，少数工况为分层流，因此设置了旋流器统一流型为环状流。

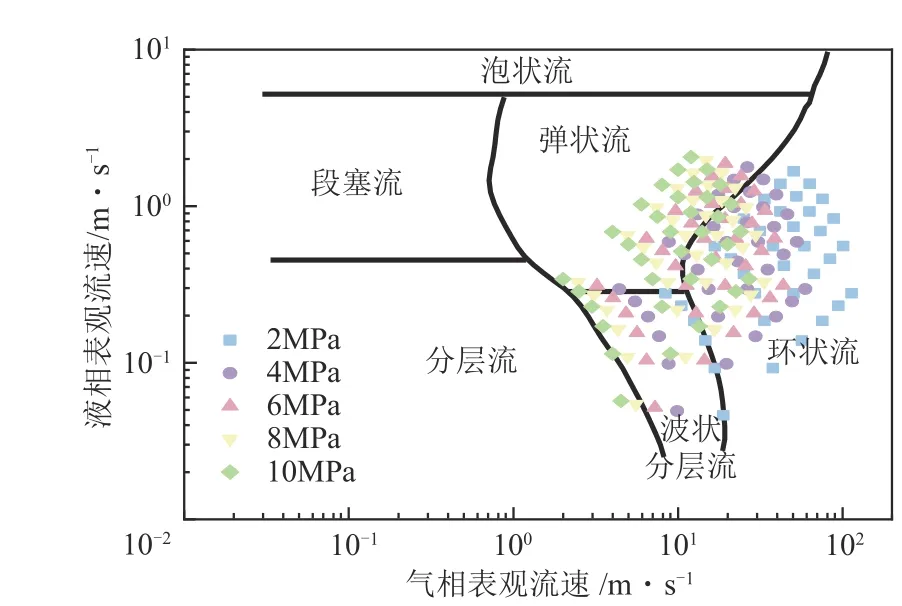
图5 试验工况在流型图上的分布

2.2 模拟结果及分析

2.2.1 相分布

以操作压力6MPa、质量流量6t/h 工况为例，截取模型XYZ轴平面x=0，观察不同含液率下的相分布情况。从图6(a)、(b)、(c)可以明显看出，由于流动工况的变化使得气液两相流经过旋流器时产生了较大的扰动，其波动情况引起的不稳定性直接反映气液两相相互作用力的影响。经过旋流器后逐渐稳定形成了明显的液膜，液膜厚度在文丘里管收缩段处达到最大值，这是因为在收缩段由于液相密度大于气相，液相会受到离心力的作用而向管中心移动，而气相同样也向管中心方向移动但所受离心力小于液相；同时液膜厚度也随着含液率的下降而减小。此时气液两相均匀分布没有液滴出现，可以看作是理想的管内相分隔状态，测量段里的三个取压点均处于管内相分隔状态下。相分隔状态下气液分离，气液两相流的流型转化为强制环状流，取压口提取的轴向压差及径向压差更为稳定，提高了双参数流量计测量的精度和可靠性。

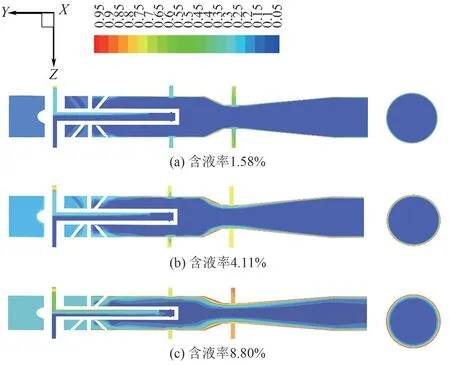
图6 不同含液率下相分布图

2.2.2 压力场与速度场分布

以操作压力6MPa、质量流量4t/h、含液率1.58%的工况为例，截取模型XYZ轴平面x=0，观察其压力分布云图、速度分布云图情况。从图7可以得知，气液两相流经过旋流器和文丘里管时有明显的压力损失，这是由于它们对流体有节流作用导致的压力降，相应的其流速也随着湍流强度的增大而增大。随着气液两相流远离旋流器、文丘里管，压力差均逐渐减小，而流速下降并也逐渐趋于稳定趋势。

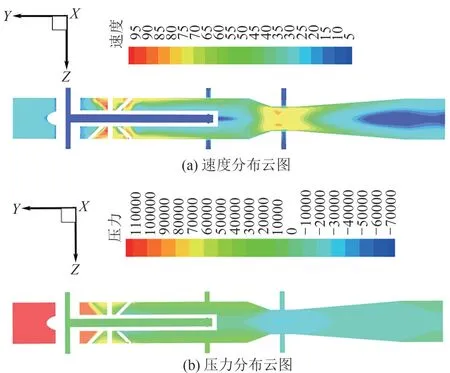
图7 管道截面分布云图

以操作压力6MPa 工况为例，截取文丘里管入口处x=125mm 到扩散段出口处x=265mm，观察不同质量流量以及不同含液率下轴向中心线的压力分布。由图8可知，气液两相在收缩段的压力降远大于喉部段的压力降，这是因为流动面积的缩小导致流动速率增大，同时也加大了气液两相间的摩阻；喉部段的压力升也远小于扩张段的压力升，这是由于液膜在扩散段受离心力作用而分散变薄，气相阻力减小而扩散使得其流速减慢，故压力升高。从图8(a)、(b)中看出当质量流量越大、含液率越小时其压力降也越快，这也是因为随着气相质量流量增大，根据连续性方程可知流体经过节流件时加速越明显，而压力降越显著。

图8 文丘里管轴心线压力分布

2.2.3 压力与密度比对压差的影响

本文进行了多种工况下的不同组模拟试验，研究不同压力、不同气液密度比对应的条件下的轴向及径向压差变化。在图9 中给出了质量流量6t/h、干度0.8 工况下操作压力、气液密度比与压差变化规律。由图可知轴向压差随着压力的增大而减小，由伯努利方程随着操作压力的增大使流体速度也会减小，导致轴向节流段的压力降；同时压力的增大导致壁面液相和中心气相的流速均减小，故壁面压力、中心压力均下降，又由于气液所受离心力也不同，故径向压差是下降的。需要注意的是，这种压差减小的趋势在一定范围内是成立的。气液对应压力下的密度由PVTsim 计算得出，当压力上升时天然气密度增大而水密度降低，因此气液密度比上升，质量流量保持不变而气相体积流量下降导致气相流速减小，对液相起到的加速作用减弱，使得气液两相摩阻变小导致压差均减小。

图9 压力与密度比对压差的影响

2.2.4 总质量流量与含液率对压差的影响

由图10 可知，轴向、径向压差随着质量流量的增大而增大，也随着含液率的减小而增大。从图9不难发现，轴向压差、径向压差的值与质量流量和含液率都存在一定的线性关系。随着质量流量的增大，气液两相流速增大使得两相摩阻增大，故压差均增大。而就含液率而言，当气相体积分数增大时会影响流体密度与黏度，从而影响流体的摩阻，气相经过喉部会受到更强的阻力导致节流压差上升；同时气体被加速会在流道形成漩涡，气柱直径加大导致湍流和涡旋强度增加，故离心压差升高。

2.3 双参数测量模型建立

根据Ferroudji 等[24-25]对环空流、环状流的实验研究，结合数值模拟结果中多因素对双压差的影响规律，发现轴向、径向压差不仅与质量流量、压力和温度有关，还与气液密度比、含液率有关。本文在雷玲卷等[17]的测量模型的基础上考虑了实际气液密度比变化对实验结果的影响，对相应的公式进行了归纳及合理改进，虚高模型的修正公式如式(21)。

式(21)中，m=1.12177；n=-0.22255；h=0.09604；a=0.08745；b=-0.0002；c=0.128；Pr为压力与大气压的比值，P/0.10125MPa；Tr为温度与室温的比值，T/293.15K。

因此新的虚高模型如式(22)。

根据Zheng 等[26]的研究可知，液相测量误差普遍大于气相测量误差。含液率变化对压力损失的影响是显著的[27]，因此在模拟基础上，本文通过在气液质量流量比公式中引入含液率来建立新的相关性提高测量精度。因此气液质量流量比可以转换表征为压差比K、含液率RL、压力P、温度T和气相弗劳德数Frg的函数，可以表示为式(24)。

在虚高模型已知的情况下，假设Frg的初值，通过式(4)、式(22)可以联立迭代得到气体质量流量；液体质量流量则可以通过下列拟合公式得到，并使用带有含液率的拟合函数对液气质量流量比进行了修正，假设RL的初值，利用式(12)、式(26)及气体质量流量可以联立迭代得到液体质量流量。式(25)、式(26)为液气质量流量比修正系数和液气质量流量比的新模型。

式(25)中，m=0.37304；n=0.47044；h=0.11669；a=0.1379；b=-9.8173×10-5；c=7.9621×10-8；d=-0.1531；e=0.01877；f=0.00076；g=-0.971。

式(26)中，a=0.08078；b=0.2819；c=1.8712；d=0.9362；m=0.0505；n=0.2662。

这个公式的核心思想是将虚高模型、质量流量比表示为多个因素的函数，其中每个因素的影响都是由相应的参数使用MATLAB拟合得到。

值得注意的是本公式仅适用于本模拟工况，均为经验公式，实际应用时需要结合具体工程问题进行调整和改进。由式(22)和式(26)可以看出，若只知Δpr和Δpa中的任何一个，均无法求出qg和ql的值；若将Δpr和Δpa组合，qg和ql就可以联立方程迭代求解得到，这便是湿气两相流双参数测量方法。修正前与修正后测量模型的R2值见表1所示。

表1 模型R2

3 现场试验与分析

3.1 试验对象

为验证本文提出的湿气双参数测量方法的有效性和适用性，于TH 油田中国石油气举中心实验室搭建湿气测量平台进行了实验，见图11所示。

图11 TH油田中国石油气举中心湿气测量平台

3.2 试验流程

在湿气测量实验平台中，通过调整柱塞泵、计量阀跟井口阀门来控制管道内流体的排量。变频器的最小工作挡位设定为1挡，以确保稳定出液。同时，保持从蓄水罐后流出的水压力稳定，以使液相流量计流过的流体在试验中压力和速度保持恒定。气体用空气压缩机产生并存储于井内，并通过调节阀控制质量流量和稳定气体流速。最终，在混合段内，液体与气体混合形成不同含液率的两相流。介于实验安全性，介质使用空气与水，此实验主要用于模拟气举后计量井口湿天然气的气液两相质量流量，实验工艺流程见图12所示。

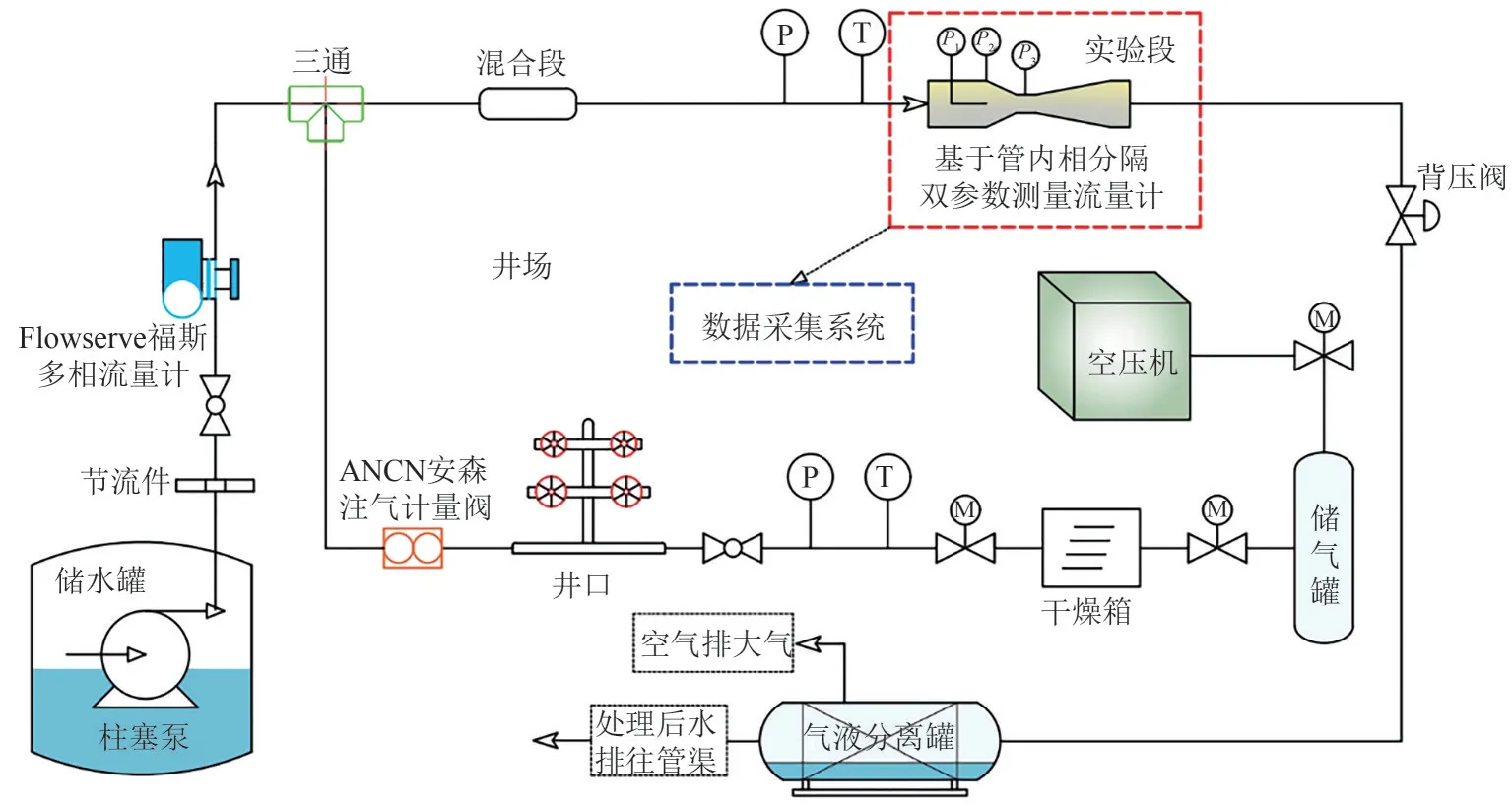
图12 实验工艺流程图

气液两相分别通过标准管路进行计量，并采用ANCN安森流量计、Flowserve福斯流量计计量单相气以及单相液流量作为对比。为了确保气液两相流的稳定性，在流量计前会接长度为20D（其中D代表管道直径）的直管段，以此达到提高流量计测量数据的准确性和稳定性的目的。由空压机将空气打入井里保持一定压力，气相流量由井口阀门及安森计量阀控制，液相流量由柱塞水泵控制，其中气相体积流量范围为600～1500m³/h，液相体积流量范围为0～8.24m³/h，由于考虑井口回压，测试压力范围取1～5MPa（本流量计最大承压能力为12MPa），实验参数范围见表2所示。测量径向压差的压差表量程为0～50kPa，测量轴向压差的压差表量程为0～200kPa，测量精度为±0.1%。测量参数如压力、温度、压差等由数据采集系统收集，再由双参数测量模型计算出气液流量。由于空气密度不同于天然气，而通过现场湿气流量计的测量性能评价表明[28]，现根据初次实验的真实数据对上述实验数据进行校准是有必要的，将不同开度下测得的安森计量阀气相流量，与双参数流量计组合标准文丘里流量表测得的气相流量对比，根据其平均误差来对气相流量进行了校准补偿，校准后进行测量实验。不同开度下需要补偿的气相流量误差见表3所示。

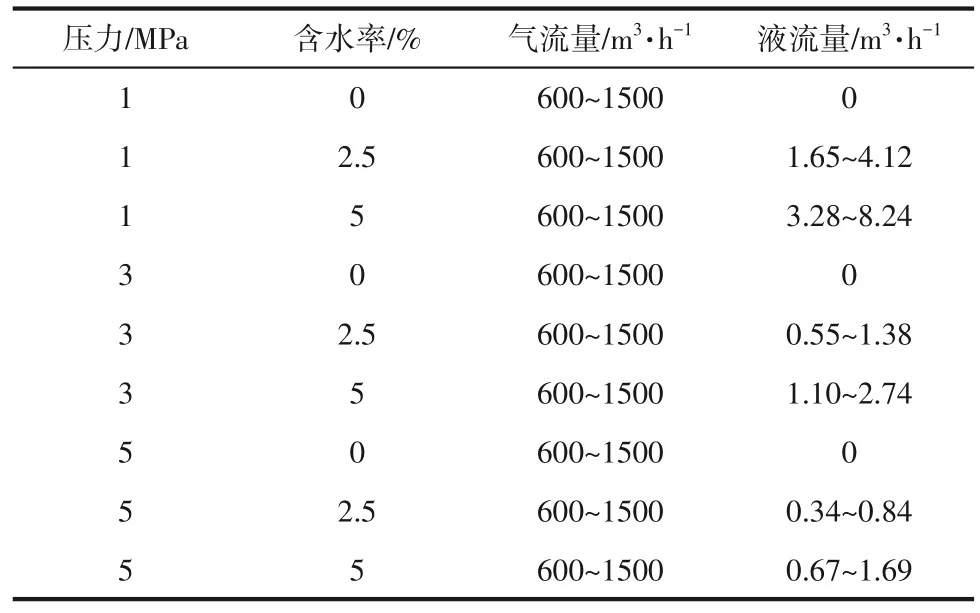
表2 实验参数范围

表3 校准补偿参数表

3.3 试验结果分析

流量测量结果见图13、图14所示。由图13可知，新双参数测量模型的实验误差较修正之前的模型具有较大改善，误差在±5%范围内，说明新模型可适用性得到了验证。通过现场分析，产生偏差的原因主要有两方面：一方面，由于气相液相模拟真实井场产气，有时是均匀的气液两相有时为一段气接着一段液，因此部分测量值产生波动导致误差增大；另一方面，水泵在低流量下无法稳定运行，并且偶尔出现流量突然增大的情况，含液使得气量测量值偏高。在图14中当含液率为0时气相测量流量的最大相对误差为3.29%，此时流量结果受含液率的影响不明显；当含液率为2.5%时气相测量流量的最大相对误差为6.51%；当含液率为5%时测量结果波动较大，组内流量最大偏差达到0.04kg/s，测量流量的最大相对误差为9.78%，这表明含液率对测量气流量具有一定的影响。综上所述，在压力相同的情况下，高含液率产生的壁面液膜更厚而使得轴向压差更小，虚高模型的值变小，故双参数测量模型某一时刻计算的气流量变大。

图13 实测值与双参数测量值的比较

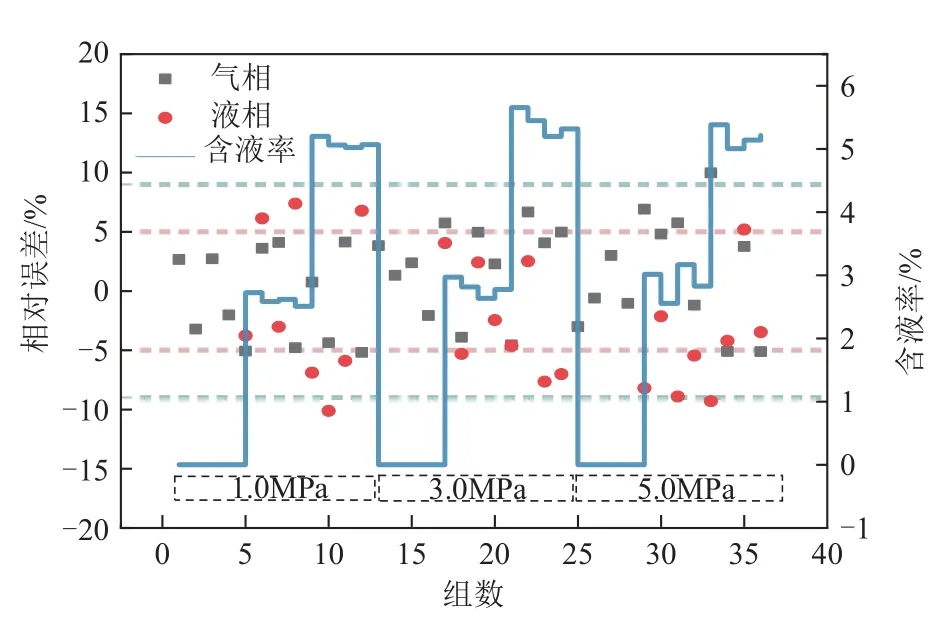
图14 气相与液相测量误差

由液相的测量结果可知，修正后液相的测量偏差明显低于本文修正前的模型，并且所测量的效果足够满足现场要求，误差在±9%范围内。当含液率为2.5%时，液相的测量流量最大相对误差为9.18%；当测试段内含液率进一步增加到5%时，液相测量流量最大相对误差则达到10.01%；随着含液率的增加，模型修正效果逐渐减小，并且从误差分布来看液相流量出现虚低现象，分析是计算的气相偏高导致后面迭代出来的液相流量降低。不同压力情况下的测量误差见表4所示，可以看出液相误差的绝对值均大于气相误差，且液相误差随着井口压力的升高而增大，推测随着井口压力升高会使高压空气将三通至混合段中一小部分的水回流导致经过双参数流量计的实际液相流量减小，此结论以便于对具体的工程应用提供指导。又从图15可知，随着含液率的增大，气相测量误差也随之增大，而含液率对液相测量误差的影响不显著。原因主要有两点：① 当含液率增大时，液相在流体中的比例较大，使得两相流体的密度逐渐增大，并且气相贡献流量的比例相对减小导致气相测量误差增大；② 考虑到文丘里管的测量灵敏度与打印精度，因此流量计对气相的测量灵敏度或者说实时测量变化可能高于液相。综上所述，含液率的增大使得气相测量误差增大，主要是因为流体密度差异和测量灵敏度差异造成的。

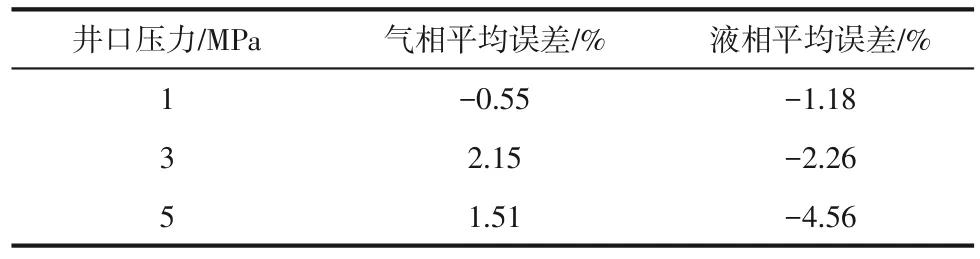
表4 不同压力情况下测量误差

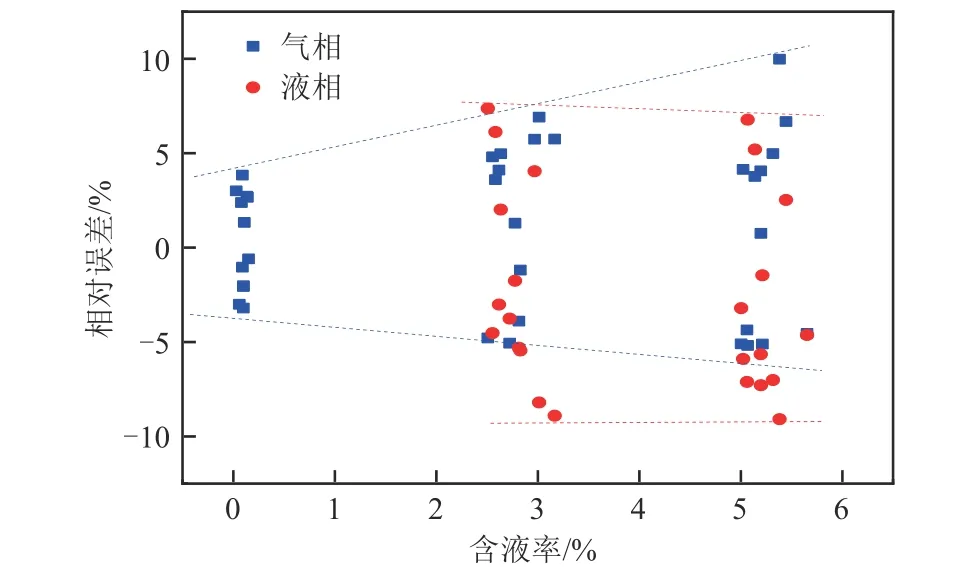
图15 含液率与测量误差相关性

虽然对比国外的Flowserve 流量计（此款流量计通过内置程序转换测量介质，能够计量液态水、天然气、二氧化碳气体、氮气等多种介质）仍存在一定的误差，但在井场气举操作中注气量对于液相的测量精度要求不高，并且成本造价是其流量计价格的几十分之一不到。通过对湿气双参数模型进行修正，相较于修正前，测量流量的相对误差最大降低幅度达到61%。可见，本文双参数测量流量计校准后一定幅度降低了管内相分隔双参数测量模型受流体中液相含率影响的程度，上面所介绍的现场实验证明了本文所述研究的可适用性及可靠性。但在实际生产中有些湿天然气的气液比极高，甚至为环雾流，液相化为分散的小液滴可能对计算结果产生较大影响，导致湿气双参数测量精度降低。因此在本文研究的实验工况下，本流量计可实现实时测量，具有较高的适用性和较低的成本，气相质量流量测量误差在±5%内，液相质量流量测量误差在±9%内均满足气举计量的需要。

4 结论

针对气液两相流中气相流量测量结果受液相含率影响的测量方法进行了改进，通过数值仿真和实验研究，验证了本文提出的双参数测量方法的正确性和可行性。

（1）通过数值模拟得到了文丘里管中湿天然气的压差特性，轴向压差、径向压差随质量流量、气液密度比的增大而增大，随压力、含液率的减小而增大。并利用其压差特征建立了新双参数测量模型，通过方程迭代分别求解出湿天然气的气液两相的质量流量。

（2）采用不锈钢材质的样机在湿气测量平台上进行了高压实验，新双参数测量模型对于含液率造成的误差大大改善并具有良好的适用性，并且校准后其气液质量流量测量误差分别在±5%和±9%内，满足TH 油田井口气举实验监控流量的要求。

（3）管内相分隔状态下的湿气双参数测量方法在高压范围内（1.04～5.05MPa）是可行的，与传统文丘里湿气测量方法相比前者消除了由流型引起的误差。因此，为天然气行业湿气测量提供了一种新的方法，可在实际中广泛采用。该方法对天然气行业中如气井、气举井的实时流量监控具有一定的工程意义。

符号说明

C—— 流出系数

D—— 文丘里进口直径，m

d—— 文丘里喉部直径，m

Frg—— 气相弗劳德数

J—— 液气质量流量比的修正系数

K—— 轴向压差与径向压差之比

L—— 虚高模型的修正系数

P—— 压力，Pa

ql，qg—— 液相和气相的质量流量，kg/s

R2—— 矫正决定系数

RL—— 含液率，%

T—— 温度，K

XL-M—— Lockhart-Martinelli参数

x—— 湿天然气干度

α—— 通过实验标定的流量系数

β—— 文丘里管入口直径与喉部直径之比

Δpa，Δpr—— 分别为为节流轴向压降、离心径向方向，Pa

ε—— 膨胀系数

ρl，ρg—— 液相和气相密度，kg/m3

Φ—— 虚高修正系数

下角标

a—— 轴向

g—— 气相

l—— 液相

r—— 径向