基于EMD的密相气力输送两相流系统内子系统相互联系和作用

付飞飞，李健

（1 潍坊学院机械与自动化学院，山东 潍坊 261061；2 大型发电装备安全运行与智能测控国家工程研究中心，东南大学能源与环境学院，江苏 南京 210096）

密相气力输送具有输送效率高、输送速度小，料气对管壁的磨损程度小等优点，研究人员针对其输送阻力特性、输送稳定性以及流型辨识等方面进行了研究[1-3]。赵凯伟等[1]针对竖直管密相气力输送研究了操作条件和煤种对输送特性及流型的影响。许盼[2]针对水平管密相气力输送研究了差压信号的香农熵和分形指数与输送稳定性之间的联系。Jin等[3]针对竖直管内粉煤密相气力输送研究了表观气速、单位管压降和输送固气比之间的关系。

上述研究主要针对较为宏观的流动特性。近年来，多位学者采用小波、经验模态分解（EMD）以及多尺度分析等方法，分析了密相气力输送两相流系统内不同尺度下差异化的动力学特征，对其有了更深入和细致的认识。金庸[4]提出利用电容层析成像技术（electrical capacitance tomography，ECT）获取信号，基于小波分析和分形分析获得多尺度频域范围，并利用多尺度能量矩阵，揭示了煤粉密相气力输送不同流型的气固相互作用机制。Fu等[5]基于EMD 和分形分析，对煤粉密相气力输送产生的静电和压力信号进行多尺度分解，进而考察了不同尺度下颗粒的运动特征。

气固两相流是颗粒流体系统，如果从系统的角度考察，又会发现一些新的现象或规律。根据系统的集成和相关特征，系统内部存在若干子系统，它们彼此之间存在相互联系和作用，这是系统存在和演变的源泉[6-7]。因此，考察子系统之间的联系和作用，将有助于揭示气固两相流系统的发展和演变规律。

气力输送水平管道中煤粉呈现上稀下浓的不均匀分布，会导致不同区域的颗粒碰撞以及受气流曳力情况不同，即颗粒的运动机理不同。运动机理相近的颗粒连同其周围的气流形成一种颗粒流体组织，即为子系统。多个子系统共同存在于两相流系统中。要考察它们之间的联系和作用，可基于子系统的波动信号，但是这些信号会叠加在一起作为系统整体的波动信号输出。因此，首先采用EMD 将密相气力输送两相流系统输出的静电信号分解成有限数目个固有模态函数（IMF），再计算其能量比重来确定主干IMFs。之后，基于静电信号EMD 分解结果、水平输送管道中颗粒的分布状况及颗粒运动机理的差异性等，明确气固两相流系统内的子系统。最后，利用主干IMFs 的主频以及方差的变化规律，分别考察子系统之间的联系和作用。

1 实验装置

1.1 密相气力输送试验系统

密相气力输送系统原理如图1所示，首先输送气体（氮气）8 进入缓冲罐7，使缓冲罐压力维持在4MPa左右，之后气体分别向系统提供充压风6、流化风5 和补充风4。料罐3 底部通入流化风使物料流化，在出口通入补充风以增强输送能力，而在顶部通入充压风可维持料罐内的压力恒定。当一个料罐里的物料离开后即进入输送管道，最终被带回另一个料罐，即完成了物料的气力输送过程。不锈钢输送管的内径为10mm。粉体物料为煤粉，密度为1350kg/m3，平均粒径为208.5μm。

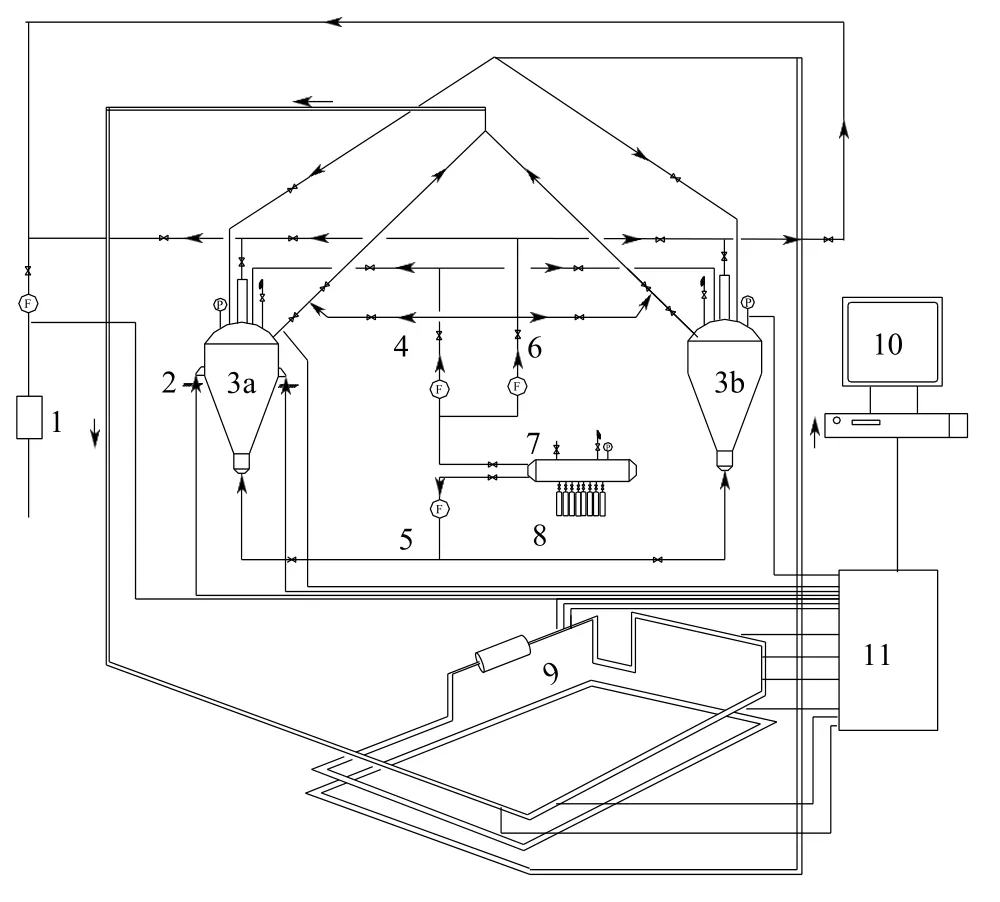
图1 密相气力输送系统原理

1.2 静电传感器

静电传感器主要由静电检测探头、调理电路和数据采集器等构成。静电传感器检测探头安装在试验系统水平输送管道的测试段即图1 中的9 位置。检测探头装置实物如图2所示，外面是金属罩，其内部主要结构如图3所示，是一段石英玻璃管（内径10mm、厚度5mm）以及布置在玻璃管外壁面的静电检测极片（轴向宽度5mm）。输送管道中的煤粉流经探头时，检测极片上产生感应电荷，电荷转移形成电流，电流经过调理电路放大后由采集器采集并传输到计算机中显示输出；采样频率为1000Hz，输出为±5V之间的电压信号。

图2 静电传感器检测探头

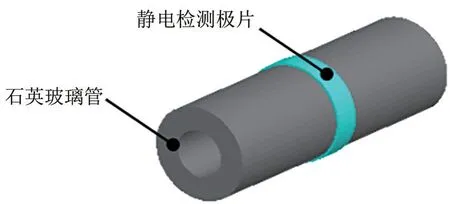
图3 探头内的主要结构

1.3 ECT系统

ECT系统由电容检测探头、检测电路、数据采集与控制电路以及成像计算机组成。ECT是一种可视化成像技术，其原理是将管道内流体的相分布信息转化为电容信息，基于此再利用图像重建算法反演出被测流体的相分布图像，ECT多用于多相流参数的在线检测和流型识别[8-9]。在本研究中采用ECT系统获取水平输送管道横截面上煤粉的分布情况，目的是为子系统的划分以及对颗粒流动状态的说明提供依据。电容检测探头安装在图1 中的9 位置，其外观与图2中的静电传感器检测探头相同。电容层析成像系统成像速度74帧/s，分辨率32×32。

2 结果与讨论

2.1 实验工况

实验进行了4个工况，各工况的输送参数列于表1（参数计算方法见参考文献[10]）。其中，表观气速与跃移速度的比值（用k表示）可估测主体颗粒是否悬浮，k＞1时，主体颗粒能够悬浮；k＜1时，少量可悬浮但主体尚未悬浮[10]。图4 所示为4 个工况的静电输出信号，每个工况的采样时间为10s，即采集10000个数据点。

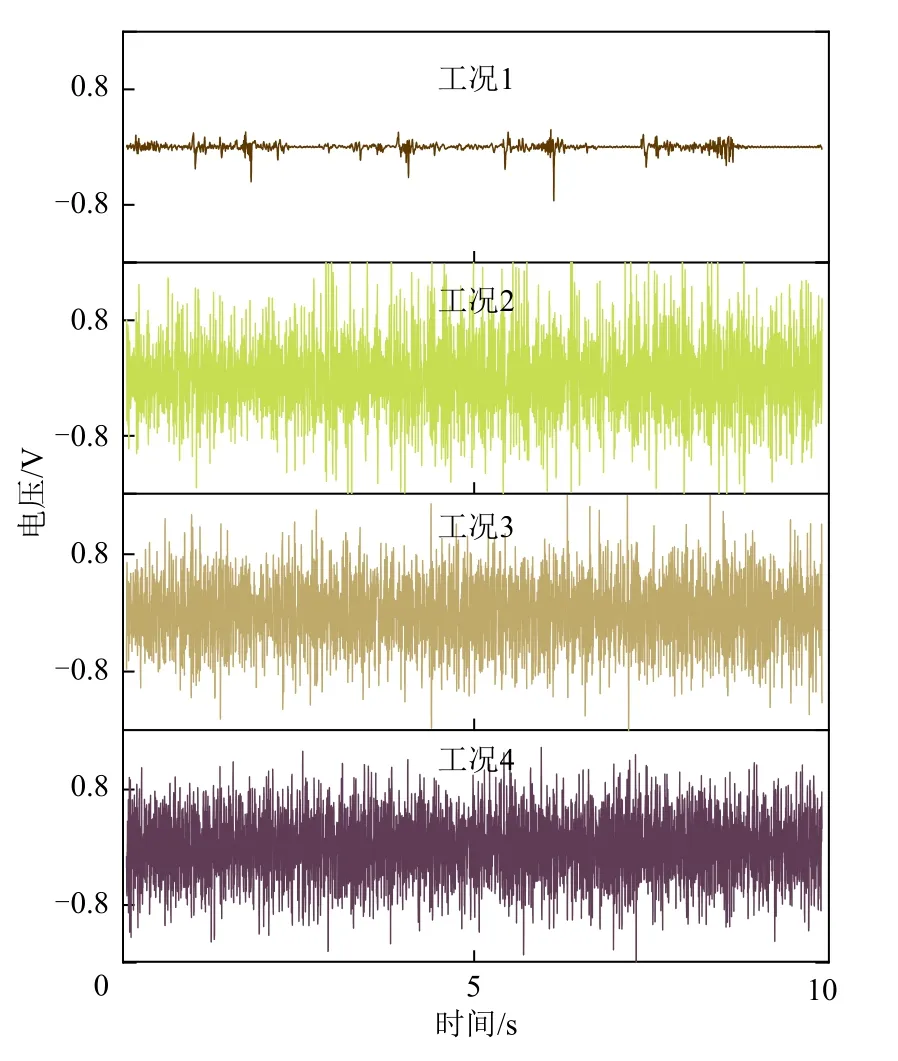
图4 各工况的静电输出信号

2.2 静电信号的EMD分解

2.2.1 EMD

EMD 能够将多分量信号分解为单分量信号的线性组合。该方法中，单分量信号被解释为局部平均值为零的一类信号，即IMF。IMF 分量必须满足以下两个条件[11]。

（1）在整个时间序列长度上，极值点和过零点的数目必须相等或至多相差一个。

（2）在任意时刻，局部最大值的包络和局部最小值的包络的均值在任一点处必须为0。

根据定义，时间序列X(t)的EMD分解如下。

首先，找出X(t)所有的极值点，然后利用其拟合出X(t)的上下包络线，得到上下包络线的均值m1，再将X(t)减去m1即可得到一个时间序列h1[式(1)]。

若h1满足上述两个条件，那它就是一个IMF，也即是X(t)分解出的一个分量；若不是，就将它看作新的时间序列，重复进行上述的处理过程[式(2)]。

式中，m11是h1的上下包络线的均值。重复k次，直到所得到的平均包络值趋于零为止，这样就得到了第1个IMF分量I1[式(3)、式(4)]。

式中，I1代表X(t)中最高频的组分。

之后，将X(t)减去I1，得到一个时间序列r1，对其进行上述同样的分解过程，得到第2 个分量I2。如此重复直到最后一个序列rn不能再被分解为止，此时rn代表X(t)的剩余项[式(5)、式(6)]。

最终，将式(5)和式(6)合并，可得到时间序列X(t)如式(7)。

2.2.2 静电信号的EMD分解结果

每个工况的静电信号均被分解成多个IMF 分量。其中，工况4的静电信号EMD分解结果如图5所示，按照频率由高到低将IMF 从上到下进行排列，越往下IMF 的波动频率越小，波动幅值也越小，因此其对原始信号的重要性就越小。IMF的重要程度大小可利用其能量占比来衡量，图6所示为4个工况下各IMF 分量的能量占比计算结果。结果表明：4个工况的情况类似，即IMF1～IMF4的能量占比各自均大于5%，所加之和均大于90%。因其他分量占比很小，不能有效代表系统中的运动信息，可以忽略，所以IMF1～IMF4 是原始静电信号中的主干分量，能够反映系统中子系统内的颗粒流体组织的运动信息。

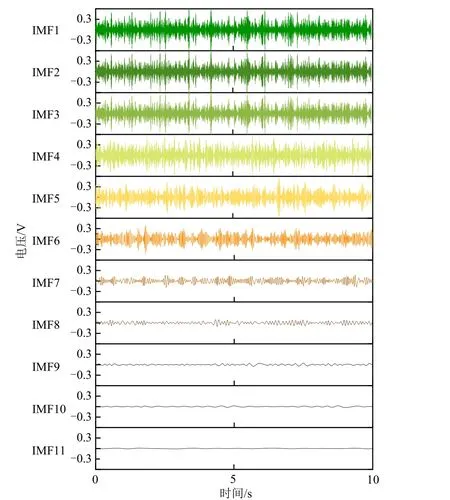
图5 工况4的静电信号EMD分解结果

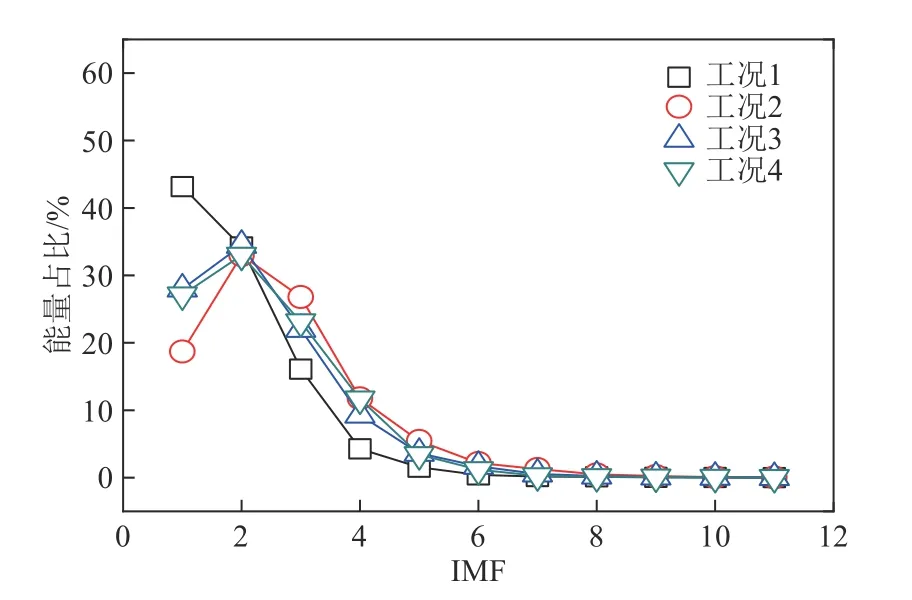
图6 各工况下IMF的能量占比分布情况

2.3 水平管道内气固两相流系统的子系统

子系统是运动机理相近的颗粒连同其周围的气流形成的一种颗粒流体组织。气力输送水平管道中煤粉呈现上稀下浓的不均匀分布，导致不同区域的颗粒碰撞以及受气流曳力情况不同，即颗粒的运动机理不同。而基于上述静电信号EMD 分解结果，认为存在4 个子系统，理由是：①依赖于EMD 分解的有效性，即分解出的IMF1～IMF4 是反映出不同运动机理的分量信号；②从运动机理上划分成4个子系统也是合理的，管道横截面上的颗粒浓度分布不均，由上往下逐渐增大，可参考ECT获得4个工况下管道横截面上煤粉分布情况的连续图像（图7 所示），其中色度条从蓝色到红色表示煤粉的相对浓度逐渐增大，根据浓度的差异，系统空间可以分成4个区域，即稀相区、交界区、浓相区以及贴壁区（划分示意见图8）。浓度不同导致颗粒碰撞以及受气流曳力情况即运动机理不同，以上4个区域内颗粒的运动机理对比情况列于表2中。

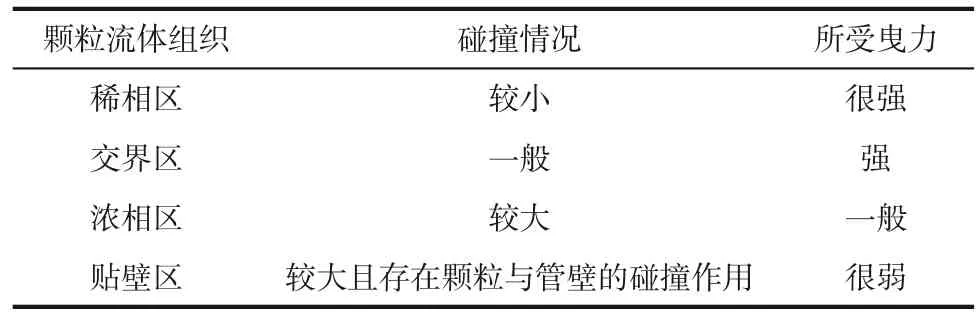
表2 子系统内颗粒碰撞和受曳力情况

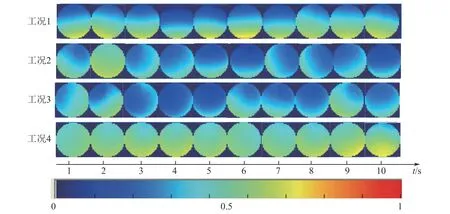
图7 煤粉分布的ECT成像图

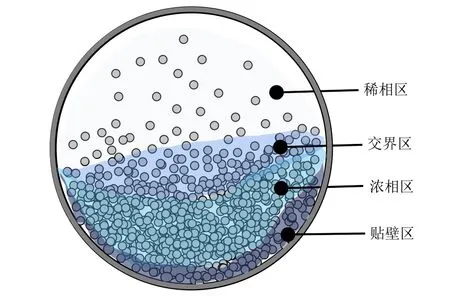
图8 水平管道中煤粉颗粒分布的示意图

基于上述分析，这4个区域内的颗粒流体组织即认为是4个子系统。IMF1～IMF4与子系统的对应关系在下文中进行阐述。

2.4 主频分析

IMF1～IMF4 均是10000 个数据点的时间序列，将其等分成10个子序列，再对每个子序列进行快速傅里叶变换（FFT） 并提取主频，便可获得IMF1～IMF4主频的变化规律，如图9 所示。首先，可确定IMF1和IMF4与子系统的对应关系。主频与颗粒速度有密切联系，颗粒速度越大，频率就越大[12-13]。IMF1的频率最大且波动相对剧烈，对应稀相区子系统内的运动情况，因为该子系统内颗粒悬浮，以单颗粒的状态运动，受气流的夹带作用明显，具有较高的速度；而IMF4 的频率最小且波动最平缓，对应贴壁区子系统内的运动情况，因为该区域内颗粒受到的摩擦及碰撞阻力最大，速度最小。IMF2和IMF3与交界区和浓相区子系统之间的对应关系尚不能明确，因为这两个子系统的运动特征并不明显。

图9 IMF1～IMF4主频的变化规律

IMF1～IMF4 的主频随工况的变化规律是一致的，均为先增大（工况1 到工况2）后近似不变（工况2 到工况4），说明子系统的颗粒速度变化规律一致，这是颗粒在子系统之间游走从而将子系统联系起来共同响应的结果。从工况1 变到工况2，表观气速增大，k由小于1变为大于1，即颗粒悬浮性得到增强，浓相区子系统内部分颗粒进入交界区和稀相区，由于它们不再对浓相区和贴壁区的颗粒造成挤压，因此这两个子系统内流动性增强，颗粒速度增大，而交界区和稀相区子系统本身受气流作用明显，颗粒速度也会增大，最终子系统内的颗粒速度均有增大。但是随表观气速的增大，质量流量也在增大，增加的悬浮颗粒在空间内游走，增大了各子系统内的颗粒浓度，由于颗粒间的碰撞作用变强反而阻碍了颗粒速度的进一步增大。所以工况2 一直到工况4，IMF1～IMF4 主频没有增大的趋势。

2.5 方差分析

图10 所示为4 个工况下IMF1～IMF4 的方差的变化情况。方差波动越大，输送越不稳定，子系统之间的相互作用就越剧烈。工况1下IMF1～IMF4的方差均非常小（几乎为零），说明子系统间的相互作用非常小。原因是：此时k＜1，主体颗粒没有悬浮，如图7中工况1下的ECT 成像图所示，主体颗粒群的表面呈现中间高边缘低的凸面（其他3个工况是凹面），这说明此时主体颗粒没有悬浮，而是集中在管底部向前滑动，管道上部虽有少量悬浮颗粒但主要是气流，因此主体颗粒和气流在各自的空间内运动，没有形成如图8 所示的典型的子系统，也就不发生相互作用。

图10 IMF1～IMF4方差的变化

工况2方差值较大，说明子系统之间有明显的相互作用。观察发现IMF1～IMF3 三者的变化规律较为一致，且与IMF4 的变化规律几乎相反，即一方增大另一方就减小。这个规律表明，子系统之间的相互作用是“竞争”。竞争是因为IMF4对应贴壁区子系统，其中颗粒的运动受气流的影响较弱，是颗粒主导的运动。而在气固两相流系统中，同时存在颗粒主导和气流主导两种运动机制，而这两种机制会相互抗衡[14]。另外3个子系统因浓度及位置等因素，受气流的作用相对更明显，是气流主导的运动，因此是颗粒主导和气流主导两种运动机制之间的竞争。竞争作用在工况3 和工况4 中得到缓解，尚存在相反的规律但是不剧烈。原因是工况2下主体颗粒虽然悬浮流动，但是k值仍相对较小，受气流的夹带作用尚不强烈，因此颗粒和气流均没有明显的主导优势，在势均力敌的情况下竞争就更加地激烈；而工况3 和工况4 下，k值变大，主体颗粒悬浮性好，气流的作用占主导。一旦有一方占主导，竞争就随之减弱，极限情况下，所有颗粒完全悬浮分散在管道，竞争就会消失。

3 结论

根据系统的特点，密相气力输送两相流系统内子系统之间必然存在相互联系和作用，根据实验可得到以下结论。

（1）子系统之间依靠颗粒在彼此之间游走而进行联系。表观气速增大时，新发生悬浮的颗粒会往管道上部空间游走，改变了本身所处的以及其他子系统的颗粒浓度，进而又改变了子系统内颗粒的受力以至于运动速度。

（2）子系统之间存在“竞争”作用。这种竞争是颗粒主导与气流主导之间的竞争，当二者势均力敌时，竞争作用激烈，一旦表观气速较大，悬浮颗粒增多到一定程度，此时气流作用占主导，竞争作用就减弱。